关于协同空战目标分配效能优化策略仿真

安 超，李战武,2，常一哲，杨海燕，刘小军

(1.空军工程大学 航空航天工程学院，陕西 西安 710038； 2．西北工业大学 电子信息学院，陕西 西安 710072； 3.空军工程大学 空管领航学院，陕西 西安 710051;4.北京航空工程技术研究中心，北京 100076)



关于协同空战目标分配效能优化策略仿真

安 超1，李战武1,2，常一哲1，杨海燕3，刘小军4

(1.空军工程大学 航空航天工程学院，陕西 西安 710038； 2．西北工业大学 电子信息学院，陕西 西安 710072； 3.空军工程大学 空管领航学院，陕西 西安 710051;4.北京航空工程技术研究中心，北京 100076)

协同空战中目标分配是否合理有效决定着作战效能的大小，已经成为一个核心决策问题。针对战场态势复杂多变，目标分配受到多种限制，对实时性要求高的问题，提出了优化策略。综合考虑空战中的作战效能和作战代价，构建目标函数，根据实战环境建立约束条件。为了满足现代空战实时快速的要求，通过引入遗传算法交叉算子和Bolzmann选择策略的方法，对人工蜂群算法进行改进，既提高了算法的搜索能力，又保证了算法的收敛速度。仿真分析表明:目标分配模型合理有效，目标分配效能得到了优化，对协同空战具有较好的实用价值。

协同空战； 目标分配； 优化策略； 改进人工蜂群算法

0 引 言

随着现代空战的日益激烈以及信息化的快速发展，单机作战的样式已经不能适应现代战争的需求，多机协同空战应运而生。协同空战中，各战机通过信息流的交互连通作用，能够有效的提高机群的探测、识别、跟踪、引导和对敌攻击能力，并能有效地交替掩护，安全退出。如何对机群合理有效地分配攻击任务，使得整体的作战效能最大化，成为协同空战的一个核心决策问题[1]。

目前，在目标分配问题中，多采用启发式算法求解，如遗传算法[2～4]、粒子群算法[5～7]、蚁群算法[8,9]等，在目标分配问题上，取得了一定的进展，但也都存在早熟停滞现象，且收敛速度较慢，无法满足当前空战快速实时性的要求。

人工蜂群算法是一种新兴的智能算法，具有收敛速度快，鲁棒性好，全局收敛的优点，但是搜索精度不高的缺点。人工蜂群算法在目标分配中的应用研究较少，主要有文献[10]通过控制种群编码熵，保留最优蜜源和次优蜜源的方式求解目标分配问题，文献[11]利用模拟退火方法对坦克分配问题进行了求解。本文通过引入遗传算法交叉算子和Bolzmann选择策略的方法，对人工蜂群算法进行改进，用于求解协同空战目标分配问题。

1 协同空战目标分配模型

协同空战中的目标分配是一个核心决策问题，是指在一定作战环境下，根据已掌握的敌我双方兵力部署情况，快速演算，综合分析，选择我方最佳的决策分配方案。目标分配是否合理有效，依赖于选择的参考指标能否有效反应实战需求，以及敌我双方的威胁系数是否真实有效，基于此建立如下模型。

假设战场想定为我方有作战飞机m架，使用相同的作战导弹，敌方有作战飞机n架，使用相同的作战导弹，需要考虑的指标如下所示:

1)敌方飞机对我方的威胁系数为α=(α1,α2,…,αn)。

2)我方飞机的目标分配决策矩阵X为

(1)

式中 xmn为我方第m架飞机对敌方第n架飞机的攻击决策，xmn=1为攻击，xmn=0为不攻击。

3)我方飞机对敌方飞机的威胁度矩阵为P，pji为我方第j架飞机对敌方第i架飞机的威胁度。

4)βji为我方第j架飞机对敌方第i架飞机攻击时所消耗的代价。

现代战争比拼的是综合国力，在作战中既要保证消灭敌人，同时又要减少消耗，也就是说花费最小的作战代价，达到最大的作战效能。基于此要求，建立如下所示的目标函数

max F(X)=w1F1(X)-w2F2(X)

(2)

式中 F1(X)为作战效能，F2(X)为作战代价，w1,w2为权重，且w1+w2=1。

根据实际空战环境，提出如下所示约束条件：

1)对于每一架敌机，都要被我方飞机攻击，同时我方攻击飞机的数量要小于临界值nc，即

(3)

2)若我方一架飞机对敌方飞机的威胁度已经达到理想状态，其他飞机就不再对其进行攻击，即

(4)

3)若我方一架飞机攻击敌方飞机所消耗的代价超出可接受值，则不对该敌机进行攻击，即

xji=0,βji>βacceptable

(5)

4)在整个攻击过程中，对目标的攻击时间不能超过允许的最大值

max{xjitji}≤Tallow

(6)

5)在攻击中，对单个目标的威胁值要大于最小接受值

(7)

1.1 敌方飞机威胁系数

敌方飞机对我方的威胁主要从相对态势来考虑，由距离威胁因子、角度威胁因子和速度威胁因子加权求和得到。

距离威胁因子为

(8)

式中 re为敌机导弹射程，ro为双方飞机距离，rm为我机导弹射程，ke为我方的电子干扰能力系数。

角度威胁因子

(9)

式中φ为敌机的进入角，φ为敌机前置角。

速度威胁因子

(10)

式中 Ve为敌机速度，Vo为我机速度。

第i个敌机总的威胁系数为

αi=λ1pdi+λ2pdi+λ3pvi

(11)

式中 λ1,λ2,λ3为加权系数，且λ1+λ2+λ3=1。

1.2 我方飞机对敌方飞机的威胁度矩阵

我方飞机对敌方飞机的威胁度也从相对态势来考虑，参照敌方飞机威胁系数的确定方法。

1.3 攻击所消耗的代价

我方第j架飞机对敌方第i架飞机攻击时所消耗的代价βji主要考虑导弹的成本与所需导弹的数量，得

βji=Cji×nji

(12)

式中 Cji为导弹的成本，nji为我方第j架飞机对敌方第i架飞机攻击时所需导弹的数量。

2 改进人工蜂群算法的目标分配方法

蜂群算法[12]在2005年被Karaboga系统提出，是一种新的随机型智能优化算法。算法中的构成要素蜜源代表了所求优化问题的可行解，蜂群主要由引领蜂、跟随蜂和侦察蜂组成。蜜源吸引引领蜂去采蜜，引领蜂在舞蹈区与跟随蜂进行信息的共享，引领蜂又根据跟随蜂的搜索方式进行位置的更新，当同一蜜源被采集次数超过了极限limit次之后，引领蜂就变为侦察蜂，产生新的蜜源进行采蜜，通过不断的进化，最终产生最优解。

2.1 跟随蜂选择策略

在原始蜂群算法中，跟随蜂按照轮盘赌的方法选择蜜源，使得算法陷入过早收敛的问题。根据文献[13]引入Bolzmann选择策略，通过对不同阶段压力大小的控制，既保证了早期种群的多样性，又保证了后期的收敛速度。

跟随蜂选择策略的概率为

(13)

式中 T=T0(0.99c-1)，T为压力，T0为初始压力，c为进化次数，fi为第i个个体的适应度值。

2.2 引领蜂的位置更新

在原始蜂群算法中，引领蜂的位置更新主要是通过跟随蜂的搜索算子实现

Xi(t+1)=Xi(t)+r×(Xi(t)-Xk(t))

(14)

式中 Xi(t+1)为新蜜源，Xi(t)为原来的蜜源，r为在[-1，1]范围内的随机数，Xk(t)为除了原来蜜源以外随机指定的蜜源。

由于Xk(t)为随机指定的蜜源，保证了较好的搜索能力，却使得开采能力不足，通过引入整个种群的最优搜索位置[14]和遗传算法的交叉过程，提高算法的开采能力。

2.3 侦察蜂搜索策略

在原始蜂群算法中，侦察蜂选择新蜜源的搜索方式随机性很强

Xi(t+1)=rand

(15)

虽然保证了蜜源的丰富性，但是收敛速度慢，且容易陷入局部最优。根据文献[15]提出的侦察蜂搜索策略可以有效避免上述问题，即

Xi(t+1)=Xi(t)×(1+(2rand[0,1]-1)×(dmin+

(16)

式中 dmin,dmax,a，b为常数，cycle为迭代次数，tmax为迭代次数的最大值。

2.4 改进算法解决目标分配步骤流程

根据上述改进的算法，对目标分配求解最优值的过程如下：

1)在假定的战场环境下，产生目标分配的初始可行解集xij，作为蜜源。

2)根据目标函数，计算各个蜜源的适应度，记录最优适应度和最优解。

3)引领蜂做邻域搜索，如果新位置的适应度高，则进行位置的更新，开采度置0，选择适应度最高的位置作为下一次开采的蜜源位置；否则，位置保持不变，开采度加1。

4)计算位置更新后的适应度，根据式(13)计算跟随蜂的选择概率，概率越大招募的跟随蜂越多，记录最优适应度和最优解。

5)将开采度与开采极限limit比较，大于开采极限，该引领蜂变为侦察蜂，按式(16)产生新的位置。

6)若达到结束条件，即达到最大迭代次数，则算法结束，输出最优解;否则,转到步骤(3)继续进行迭代。

3 算例分析

3.1 迎头攻击

假设战场想定为我方飞机与敌方为迎头遭遇，我方为3机编队，敌方为4机编队，敌我双方的位置与性能参数如表1所示。

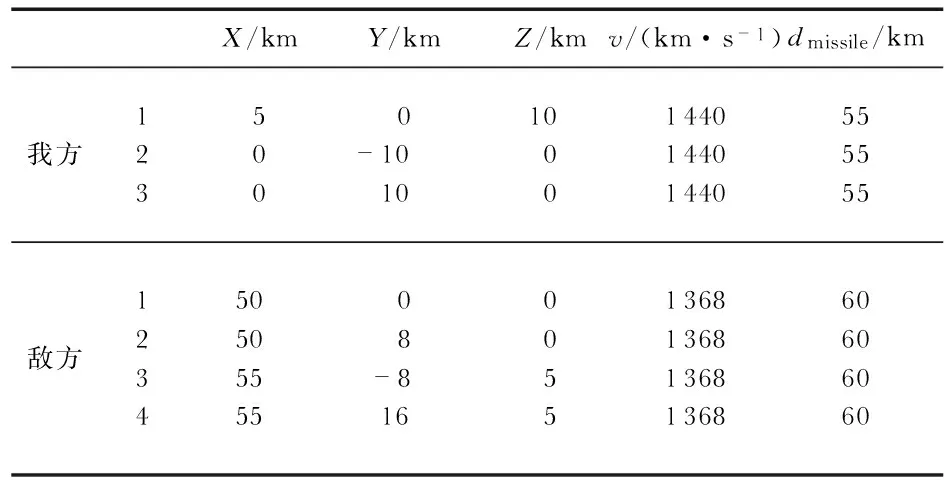
表1 迎头攻击敌我双方的位置与性能参数

目标函数权重的确定采用信息熵法，具体步骤参见文献[16]得到w1=0.648 6,w2=0.351 4，由此形成敌我双方的空战能力矩阵见表2和表3。

表2 我方对敌方的空战能力矩阵

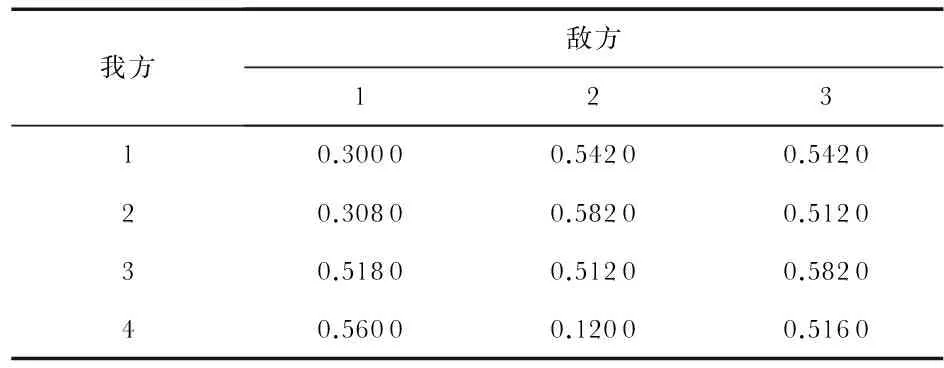
表3 敌方对我方的空战能力矩阵

改进人工蜂群算法中的参数设置：种群数目N=100，向量维数D=4，迭代次数n=100，最大适应度(目标函数)滞留次数N2经多次实验验证，选取25比较合理，最小适应度滞留次数N1=25。通过仿真实验得到最佳分配方案见表4，仿真结果见图1。

表4 空战最佳分配方案

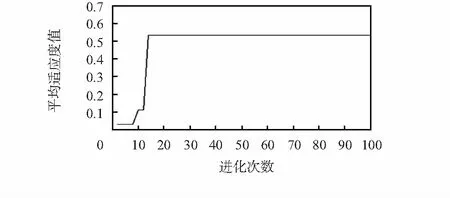
图1 迎头攻击时进化过程曲线Fig 1 Curve of evolution process in head-on attack

由上可知，我1号机攻击敌3号机，我2号机攻击敌2号机，我1号机攻击敌3,4号机的分配方案，我方对敌方的空战优势最大。算法的收敛速度较快，在14代左右趋于收敛。

3.2 与其他算法进行比较

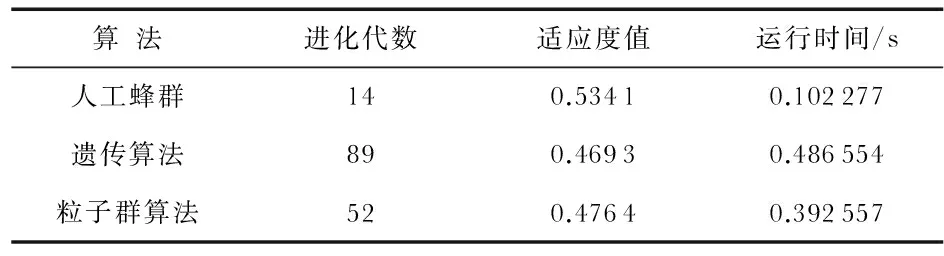
遗传算法作为比较成熟的算法，被广泛应用于目标分配问题，粒子群算法作为一种有效的全局寻优算法，也取得了较好的进展，现将改进人工蜂群算法与遗传算法和粒子群算法在迎头攻击想定条件下进行比较，仿真结果如下图2和表5所示。

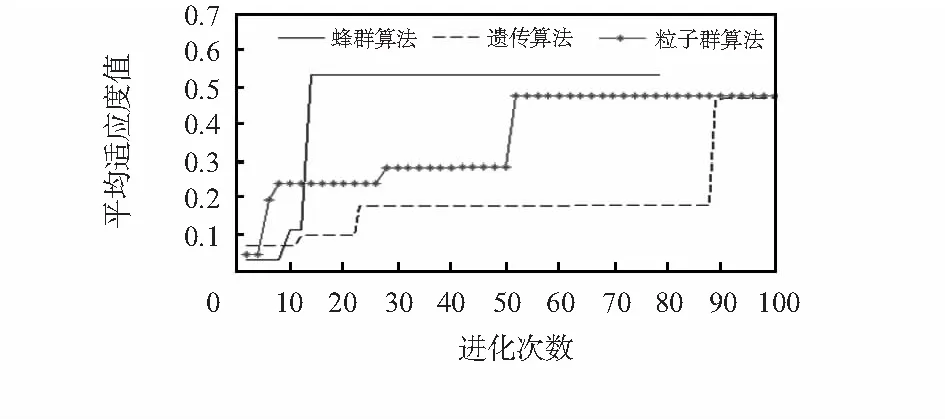
图2 三种算法在迎头攻击想定中的曲线Fig 2 Curve of three algorithms in the head-on attack

算法进化代数适应度值运行时间/s人工蜂群140.53410.102277遗传算法890.46930.486554粒子群算法520.47640.392557

从图2和表5中可以看出，改进人工蜂群算法在14代收敛，比遗传算法的89代减少了84.27 %，比粒子群算法的52代减少了73.08 %，收敛速度快；适应度值比较理想，分别比遗传算法和粒子群算法高出13.81 %和12.12 %，没有陷入局部最优；分配速度快，运行时间短，分别比遗传算法和粒子群算法快375.72 %和283.82 %。

通过上述仿真实验，可以看出:改进人工蜂群算法在目标分配过程中，实现了效能的优化。对于当前协同空战战斗激烈，作战时间短，需要快速决策的问题有较好的实用价值。

4 结 论

本文从协同空战中目标分配问题出发，建立了包括作战效能和作战代价的目标模型，通过对人工蜂群算法改进，进行了仿真实验，结果表明该方法实现了目标分配效能的优化，对当前空战具有较好的实用价值。同时，对于作战想定、初始值和算法参数的确定还需要进一步的探讨研究，以便更好的符合作战实际。

[1] Luo Delin，Yang Zhong，Duan Haibin，et al.Heuristic particle swarm optimization algorithm for air combat decision-making on CMTA[J].Trans of Nanjing University of Aeronautics and Astronautics,2006,23(1):20-26.

[2] 杨山亮，黄 健，刘 洋,等.基于遗传算法的联合火力WTA问题研究[J].计算机仿真，2012，29(3)：61-63，136.

[3] 李湘清，孙秀霞，王 栋,等.基于遗传算法的UCVA动态任务分配模型及研究[J].系统仿真学报，2008，20(16)：4387-4403.

[4] 饶卫平，杨任农，雷晓义,等.基于多智能体遗传算法的战术航段优化[J].传感器与微系统，2014，35(3):40-48.

[5] 叶 文，朱爱红，欧阳中辉,等.基于混合离散粒子群算法的多无人作战飞机协同目标分配[J].兵工学报，2010，31(3)：331-336.

[6] 范成礼，邢清华，郑明发,等.基于IDPSO的武器目标分配优化算法[J].系统工程与电子技术，2015，37(2)：336-342.

[7] 王 波，王灿林，梁国强.基于粒子群寻优的D-S算法[J].传感器与微系统，2007，26(1):84-86.

[8] 陈 昊.基于OpenMP的并行蚁群算法求解协同空战火力分配[J].传感器与微系统，2013，32(1)：20-24.

[9] 陈 旭，蔚承建，吉 军,等.自动机制设计中一种改进的混沌蚁群算法[J].传感器与微系统，2011，30(10)：144-147.

[10] 毛艺帆，张多林.改进的人工蜂群算法求解武器目标分配问题[J].军事运筹与系统工程，2015，29(1)：30-80.

[11] 常天庆，陈军伟，张 雷,等.坦克分队WTA问题的改进人工蜂群算法[J].装甲兵工程学院学报，2015，29(5)：69-76.

[12] 杨淑莹，张 桦.群体智能与仿生计算—Matlab技术实现[M].北京：电子工业出版社，2014.

[13] 丁海军，冯庆娴.基于Bolzmann选择策略的人工蜂群算法[J].计算机工程与应用，2009，45(31)：53-55.

[14] Zhu G P，Kwong S.Gbest-guided artificial bee colony algorithm for numberical function optimization[J].Applied Mathematics and Computation,2010,217(7):3166-3173.

[15] Banharnsakun A，Achalakul T，Sirinaovakul B.The best-so-far selection in artificial bee colony algorithm[J].Applied Soft Computing，2011,11(2):2888-2901.

[16] 郭 辉,徐浩军,刘 凌.基于区间数的预警机作战效能评估[J].系统工程与电子技术,2010,32(5):1007-1010．

Optimization strategy simulation on target allocation effectiveness of cooperative air combat

AN Chao1，LI Zhan-wu1,2，CHANG Yi-zhe1，YANG Hai-yan3，LIU Xiao-jun4

(1.College of Aeronautics and Astronautics Engineering,Air Force Engineering University, Xi’an 710038,China;2.School of Electronics and Information,North Western Polytechnical University, Xi’an 710072,China;3.College of ATC Navigation,Air Force Engineering University, Xi’an 710051,China;4.Beijing Aeronautical Technology Research Center,Beijing 100076,China)

Target allocation is a core decision question for cooperative air combat,which decides the combat effectiveness.Optimization strategy is proposed to solve the problem that battle situation is complex,various target allocation is restricted and demand for real time is high.The target function is established,synthetically considering combat effectiveness and combat cost.Restraint condition is based on actual environment.In order to satisfy the demand for real time and fast air combat,artificial bee colony algorithm is modified through bringing in genetic algorithm cross operator and Bolzmann selection strategy.It not only improves the search ability of algorithm,but also assures the convergence speed of algorithm.The result indicates that target allocation model is reasonable and the target allocation effectiveness is optimized,it has practical value for cooperative air combat.Key words:cooperative air combat； target allocation； optimization strategy； modified artificial bee colony algorithm

10.13873/J.1000—9787(2016)11—0040—04

2016—08—19

TP 18

A

1000—9787(2016)11—0040—04

安 超(1987-)，男，山东泰安人，硕士研究生，主要研究方向为先进航空火力控制原理与技术。