有向异构传感器网络覆盖优化算法*
王昌征,毛剑琳,付丽霞,郭 宁,曲蔚贤
(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)
有向异构传感器网络覆盖优化算法*
王昌征,毛剑琳,付丽霞,郭 宁,曲蔚贤
(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)
针对有向异构传感器网线随机部署产生覆盖重叠和盲区这一问题,受到虚拟势场算法的启发,提出了基于虚拟势场的有向异构传感器网络覆盖优化算法(PCADH)。以有向感知模型为基础,引入重叠质心、有效质心和虚拟边界质心的概念,对有向异构传感器网络进行虚拟受力优化、节点往复运动优化和边界优化处理。仿真结果表明:算法可以快速有效地提高有向异构无线传感器网络的覆盖率。
有向异构传感器网络; 虚拟势场; 节点运动; 边界优化; 覆盖优化
0 引 言
目前,有很多学者已经对有关有向传感器网络、异构传感器网络的覆盖控制进行了研究[1,2]。文献[3]引入了有向感知模型进行覆盖的研究。文献[4]首次引入了虚拟势场的方法来优化覆盖增强问题。在此基础上,文献[5]引入质心的概念,结合虚拟势场研究覆盖增强问题;文献[6]引入了虚拟节点和角度自我调节机制以提高网络覆盖;文献[7]加入了计算几何改进虚拟力算法来解决异构无线传感器网络的覆盖问题;文献[8]结合简单随机抽样理论和最优化算法对异构无线传感器网络的覆盖问题进行优化。以上的研究,只是针对有向传感器网络或者异构传感器网络进行研究,很少有对有向异构传感器网络覆盖问题的研究。
本文提出了基于虚拟势场的有向异构传感器网络覆盖优化算法(potential field-based coverage algorithm for directional heterogeneous,PCADH),仿真结果表明:算法可以有效提高覆盖率。
1 有向异构传感器网络感知模型与覆盖问题
1.1 有向感知模型
有向感知模型[9]是一个扇形的感知区域。可以表示成一个四元素组成的向量组,即D(Mi(xi,yi),Ri,Vi(t),α)。如图1所示,Mi(xi,yi)为节点的坐标位置; Ri为节点的感知半径;单位向量Vi(t)为t时刻节点的感知方向。特别指出,θi为节点从t1时刻到t2时刻感知方向的变化值。α为节点的感知夹角,其中,β=2α表示该扇形感知区域的视角。半径异构的有向异构传感器网络满足半径同构传感器网络有向感知模型。
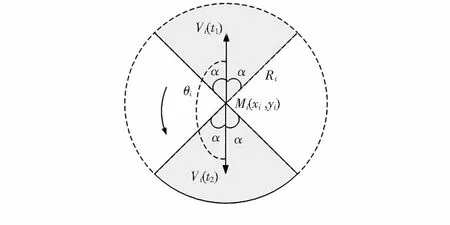
图1 有向感知模型Fig 1 Directed perception model
1.2 有向异构传感器网络覆盖问题描述
首先假设:节点随机初始部署以后,节点的位置不变;节点可以通过绕自身转动的方式来调节点的主感知方向;节点能获取自身的位置坐标信息和感知方向信息。


(1)
式中 Vi为N个节点的感知方向向量组;SΩ为研究区域面积。
2 有向异构传感器网络覆盖优化算法
2.1 虚拟受力优化分析
为了研究方便,本文首先做以下定义:
定义1 在研究区域Ω中,节点i和j的欧氏距离小于2倍的Ri,其中,Ri≤Rj,称节点i和j互为邻居节点。
定义2 如果节点i和j互为邻居节点,那么节点i和节点j的覆盖重叠区域为Si∩Sj。其中,将覆盖重叠区域的质心称为重叠质心。
定义3 如果节点i和j互为邻居节点,那么节点i的有效覆盖区域为Si-Si∩Sj。其中,将有效覆盖区域的质心称为有效质心。
如图2所示,节点i的有效覆盖区域为Si1,节点j的有效覆盖区域为Sj2;重叠区域为Sij;节点i的有效质心点为O(Si1),节点j的有效质心点为O(Sj2),重叠质心点为O(Sij)。
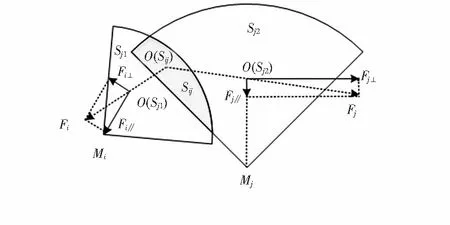
图2 质心虚拟受力分析Fig 2 Analysis on virtual force of mass center
研究区域Ω的指定质心点离散分布,因此,指定质心点坐标O(x,y)可以通过离散化方法求得,公式如下
(2)
式中 xi为指定质心的横坐标;yi为指定质心的纵坐标;num为研究区域中指定质心的个数。
两个电荷之间受斥力的作用,类比到质心的受力分析。如图2所示,虚拟斥力Fj的模型可以类比表达为
(3)
式中 k为常数系数; Dis为重叠质心点O(Sij)与有效质心点O(Sj2)之间的欧氏距离;v为所受的虚拟斥力Fj的方向。
如图2所示,斥力Fj可以分解成两个分力Fj∥和Fj⊥。分力Fj⊥是使节点改变感知方向的分力;分力Fj∥是使节点位置移动的分力。本文规定了节点的位置不能改变。所以,使节点移动的分力Fj∥不起作用,可以忽略。分力Fj⊥可以导致节点的感知方向发生变化,则节点j感知角度的变化公式为
(4)
节点受到斥力的作用,就可以改变节点的感知方向。当分斥力Fj⊥=0时,覆盖控制基本达到最优。
2.2 节点往复运动优化分析
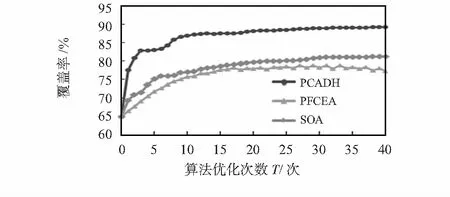
在有向异构传感器网络中,普遍存在节点往复运动的问题。假设节点j与i,k 均是互为邻居节点。如图3所示,有效质心O(Sj2)受到覆盖重叠区域Sij的斥力Fij,受到覆盖重叠区域为Sjk的斥力Fjk。斥力Fij可以分解成分力Fij∥和分力Fij⊥,斥力Fij可以分解成分力Fij∥和分力Fij⊥。其中,因为节点位置固定,所以,分力Fij∥和分力Fik∥不起作用,可以忽略。那么,当分力Fij⊥和分力Fjk⊥大小相差很小时,而且受设定的转动角度的限制。当Fij⊥>Fik⊥时,节点感知方向往右转动一个角度;旋转之后就导致了Fij⊥ 图3 节点运动受力分析Fig 3 Force analysis of node movements 针对该问题,本文设置了一个节点停止运动的阈值w,w1是分力Fij⊥和分力Fjk⊥的差值的绝对值,即w1=|Fij⊥-Fjk⊥|。当分力Fij⊥和分力Fjk⊥的差值的绝对值小于w1时,则节点就停止转动。这样就可以避免节点的往复运动,提高算法的收敛性。 2.3 节点边界优化处理 边界节点到边界的距离小于感知半径,导致了大部分的覆盖区域都在研究区域的边界以外,影响了网络覆盖性能。如图4所示,节点i是一个边界节点。本文提出的有向异构传感器网络边界节点处理方法:增加一个感知半径最大邻居节点j;质心点O(Si)与质心点O(Sj)的连线与边界线垂直。假设不存在覆盖重叠区域,则质心点O(Si)受到质心点O(Sj)的虚拟斥力可以表达为 (5) 式中 k为常数系数;Dis1为节点i与邻居节点j之间的欧氏距离;λ为所受的虚拟斥力Fj的方向。 图4 边界节点受力分析Fig 4 Force analysis of boundary nodes 节点i受到虚拟斥力Fj的作用以后,节点i的感知方向会发生变化,则变化角度θc可以表示为 (6) 式中 θc为边界节点i完成边界优化感知角度的变化量;Fjmax为斥力的最大值,用来限制斥力的改变,是一个与最大感知半径有关的常量;θmax为边界节点i感知角度变化的最大值,用来限制角度的变化,是一个常量。而且,规定了一个覆盖面积的阈值w2,阈值w2与节点i的半径Ri有关。当节点i受到虚拟斥力Fj的作用,感知方向发生变化。当节点i的覆盖区域面积大于阈值w2时,节点i就停止转动。 2.4 PCADH算法描述 输入:异构节点的个数、位置坐标信息、半径的取值范围与取值方法、感知方向信息、感知夹角信息。 输出:各个异构节点最后的感知方向。 t←0; 获取有向异构传感器网络节点Mi(xi,yi)以及它的邻居节点的相关信息; 规定PCAHD算法的循环次数; While (t for i = 1 ∶N if Mi是边界节点 构建半径最大的有向异构节点Mj为虚拟邻居节点; While Mi是边界节点 计算节点Mi受到节点Mj的虚拟斥力 ; If节点Mi受到的虚拟邻居节点Mj的虚拟斥力Fj 计算节点Mi的转动角度θc; else 节点Mi停止转动; end; end; else if节点Mi与邻居节点之间存在覆盖重叠区域; 计算节点Mi受到的两个邻居节点的虚拟斥力分力Fji⊥和Fki⊥; if节点Mi存在节点的往复运动情况 else 节点Mi停止转动; end; end end; end; 获取有向异构节点Mi以及邻居节点的位置、感知方向相关信息; t←t+1; end 3.1 算法实例仿真 本文通过Matlab R2012a对有向异构传感器网络的覆盖问题进行仿真。仿真区域为500 m×500 m;节点个数N为70个;节点感知半径Ri为[60,90]范围内的70个随机数;感知夹角α为45°;区域视角β为90° 如图5所示,为初始(t=0)覆盖图和初始覆盖率P0=64.96 %。图6(d)为PCADH优化的覆盖图与覆盖率。 图5 初始覆盖图Fig 5 Effect picture of initial coverage 图6 PCADH优化效果图Fig 6 Effect picture of PCADH optimization 从图5、图6可以看出:初始覆盖率经过1次优化以后,提高幅度达到了12.59 %,优化效果很明显。随优化次数的增加,提高幅度变缓。 70个有向异构传感器节点经过PCADH算法优化1~40次的覆盖率变化图,如图7所示。从图中可以看出,经过PCADH算法优化以后,覆盖率得到了大幅度的提升。尤其是在前10次优化,提高幅度最为明显,提高了22.03 %,10次以后提高就变的缓慢。变化趋势显示了算法具有良好的收敛性。 图7 70个节点不同算法覆盖率优化趋势Fig 7 Coverage rate optimization trend of 70 nodes with different algorithms 3.2 仿真结果对比 从图7中可以看出,本文提出的PCADH算法,在第一次优化就可以大幅度的提高网络的覆盖率。且整个过程的优化效果比SOA[7],PFCEA[8]算法提高明显。此外算法PCADH优化8次后,基本达到了最优的覆盖率,比其他两种算法的收敛速度明显要快。 在规定的研究区域随机部署50,70,90,110个传感器节点,感知半径Ri为[60,90]范围内50,70,90,110个随机数,三种算法PCADH,SOA,PFCEA经过40次优化以后,可以得到覆盖率提升幅度P′与传感器节点个数的关系,如图8所示。可以看出,无论传感器节点个数多少,经过40次算法PCADH优化以后,网络覆盖率提升幅度都比其他两种算法有大幅度提升。 图8 40次优化覆盖率提高幅度Fig 8 Increasing of 40 times optimal coverage rate 本文提出的PCADH算法,能够很大幅度地提高有向异构传感器网络的覆盖率,且具有良好的收敛性和收敛速度。在后期的工作中,应该在对有向异构传感器网络的覆盖问题进行研究的基础上,考虑障碍物对有向异构传感器网络的覆盖影响。 [1] 张春华,刘方爱,申志远.一种新的异构无线传感器网络分簇算法[J].传感器与微系统,2013,32(6):143-146. [2] 李 明.异构传感器网络覆盖算法研究[D].重庆:重庆大学,2011. [3] Ma Huadong,Liu Yonghe.On coverage problems of directional sensor network[C]∥Proc of International Conference on Mobile Ad Hoc and Sensor Networks,2005:721-731. [4] Howard A,Mataric M J,Sukhatme G S.Mobile sensor network deployment using potential field:A distributed scalable solution to the area coverage problem[C]∥Proceedings of the 6th International Conference on Distributed Autonomous Robotics Systems,New York,USA:ACM,2002:299-308. [5] 程卫芳,廖湘科,沈昌祥.有向传感器网络最大覆盖调度算法[J].软件学报,2009,20(4):975-984. [6] 陈义军,白光伟,张进明,等.基于虚拟势场的有向传感器网络覆盖增强算法的改进[J].小型微型计算机系统,2013,34(2):243-246. [7] 冯秀芳,关志艳,全欣娜,等.基于虚拟力的异构节点网络覆盖增强算法[J].计算机工程,2009,35(5):103-105. [8] 杜晓玉,孙力娟,郭 剑,等.异构无线传感器网络覆盖优化算法[J].电子与信息学报,2014,36(3):696-702. [9] 戴 宁,毛剑琳,付丽霞,等.基于虚拟势场的有向传感器网络覆盖优化算法[J].计算机应用研究,2014,31(3):905-907. 毛剑琳,通讯作者,E—mail:km_mjl@aliyun.com。 Coverage optimization algorithm for directional heterogeneous sensor networks* WANG Chang-zheng,MAO Jian-lin,FU Li-xa,GUO Ning,QU Wei-xian (Faculty of Information Engineering and Automation,Kunming University of Science and Technology, Kunming 650500,China) Aiming at problem of coverage overlapping areas and blind spots that nodes deployed randomly in directional heterogeneous sensor networks,introduce a virtual potential field-based coverage algorithm for directional heterogeneous (PCADH) networks inspired by virtual potential field algorithm.Through involving concepts of overlapping centroid,effective centroid and virtual boundary centroid to the model,this algorithm carries out optimization processing of virtual force,node advance and return movements and boundary in directional heterogeneous networks based on directed perception model.Simulation results show that the proposed algorithm can improve coverage rate of directional heterogeneous sensor networks rapidly and effectively. directional heterogeneous sensor networks;virtual potential field;node movements;boundary optimization;coverage optimization 10.13873/J.1000—9787(2016)11—0132—04 2016—01—06 国家自然科学基金资助项目(61163051);云南省应用基础研究基金资助项目(2009ZC050M) TP 393 A 1000—9787(2016)11—0132—04 王昌征(1990-),男,山东青岛人,硕士研究生,主要研究方向为无线传感器网络覆盖研究。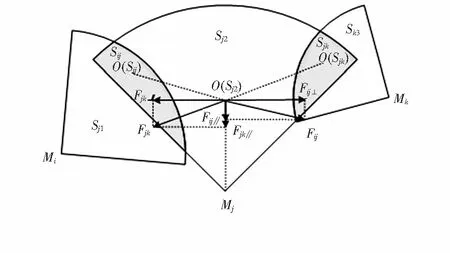


3 算法的仿真结果与分析



4 结 论

