柔性涡流阵列传感器的磁场计算分析*
曹青松,毕彬杰,周继惠
(华东交通大学 机电工程学院,江西 南昌 330013)
研究与探讨
柔性涡流阵列传感器的磁场计算分析*
曹青松,毕彬杰,周继惠
(华东交通大学 机电工程学院,江西 南昌 330013)
设计了一种由6个阵列单元(螺旋线圈)所组成的柔性涡流阵列传感器,基于电磁场理论建立柔性涡流阵列单元的电磁场模型,推导出柔性阵列单元线圈径向和轴向的磁场强度计算公式,仿真分析阵列单元线圈磁场强度与电流、线圈间隙、内外径等参数的关系,对柔性涡流阵列传感器的发展具有一定参考价值。
柔性涡流阵列传感器; 裂纹检测; 磁场强度; 螺旋线圈
0 引 言
目前常规无损检测方法主要有五种:超声、射线、磁粉、渗透和涡流检测。 其中涡流检测是利用电磁感应原理,通过测定被测工件内感生涡流的变化来评定导电材料的某些性能或发现缺陷无损检测方法[1]。然而,由于某些被测工件的结构比较特殊,一般的电涡流检测很难对其进行检测。最近出现一种新型柔性涡流传感器,该传感器是以柔性材料为基底,在柔性基底上侵刻出多个螺旋线圈,形成柔性涡流阵列传感器[2]。其不仅具有普通阵列传感器的优点,还具有良好的柔韧性,而且结构形式灵活多样,可根据被测物体任意布置,特别适合特殊结构被测工件的无损检测。
徐瑶等人[3]针对直升机旋翼应力检测的需求,研制了一种新型平面柔性涡流传感器;唐莺等人[4]采用有限元法仿真分析工作频率对平面柔性涡流传感器性能的影响;Hardy L等人[5]研制了由多个偏平磁线圈组成的低分辨率矩阵传感器,用于平坦金属表面缺陷的检测与识别。杜金强等人[6]通过矩形柔性涡流阵列传感器对金属结构的裂纹进行定量检测,并且分析了传感器对提离距离的响应特性;陈祥林等人[7]采用了柔性印刷电路板工艺制作新型接近式电涡流传感器阵列及测试系统,以实现大面积曲面间微小间隙的实时监测;丁天怀等人[8]针对柔性电涡流传感器实现大面积金属曲面部件位置实时监测,对电涡流传感器的测试技术进行研究。柔性传感器阵列的研究已经在接近式、无损检测以及机器人等领域得到广泛重视和运用[9,10]。
基于上述背景,本文研究柔性涡流阵列单元径向和轴向的磁场强度公式,分析阵列单元线圈径向、轴向磁场强度与电流、螺旋线圈间隙等参数的关系。
1 柔性涡流阵列传感器的结构与工作原理
设计一种由6个完全相同的阵列单元(螺旋线圈)和由各线圈引线形成的总电缆线所组成的柔性涡流阵列传感器,如图1所示。r1和r2分别是螺旋线圈的内外径,为了防止螺旋线圈之间磁场的相互影响,相邻螺旋线圈的间距b设计为线圈外径r2的2倍。各螺旋线圈的输入电流由
一个激励输入信号提供,各线圈的输出分别向外引出一条引线,形成总电缆线。总电缆的各条输出线分别与各自的处理电路相连,信号输出采用分时电路进行处理。
柔性涡流阵列传感器的工作原理:当螺旋线圈通入交流电流时,线圈周围就会产生交变磁场,如果将金属导体材料移入此交变磁场中,金属材料表面就会感应出电涡流,而此电涡流又会产生一个磁场,该磁场方向与原线圈磁场方法正好相反,从而减弱了原磁场。如果被测工件表面或近表面存在缺陷时,将影响涡流的强度和分布,涡流的变化又会引起线圈的阻抗变化,因此,工件缺陷的检测可以通过测量传感器阵列内各阵列单元磁感应阻抗的变化。

图1 柔性涡流传感器结构图Fig 1 Structure diagram of flexible eddy current sensor
2 柔性涡流阵列传感器磁场强度建模研究
柔性涡流阵列传感器各个阵列单元的磁场强度不会叠加,阵列式的设计是为了实现大面积范围的高速测量,并能有效地提高传感器系统的测试速度、测量精度和可靠性。因此,只需对单个阵列单元的螺旋线圈磁场强度进行分析。
根据周长相等原则,将螺旋线圈磁场强度等效为由多个同心圆环磁场强度的叠加,并以单个圆环线圈为例,先对其磁场强度进行研究,如图2所示。由于单个圆环线圈产生的磁场具有对称性,因此,只需要计算在y0z平面内的磁场分布即可,取Bx,By和Bz分别为磁场的切向、径向和轴向分量,载有电流I,半径为R的圆环线圈。在圆环线上任一点处A(x,y,0)的电流元Idl及其指向场P=(0,r,z)点的矢量l→可以表示为

图2 螺旋线圈与圆环磁场模型Fig 2 Models for spiral coil and circle ring magnetic field
Idl→=I(dxi→+dyj→)
(1)
l→=-xi→+(r-y)j→+zk→
(2)
将式(1)、式(2)代入毕奥—萨伐尔公式,展开并整理,可以得到P处的磁场为
(3)
式(3)右边,线性积分是沿圆周L进行的。其中,r,z为定值,而x和y则为变量。用坐标变换且取φ的积分限为(-π/2,3/2π),B→可表示为
(4)
式(4)右边第一项的积分即为B→的切向分量
(5)
即圆环线圈的磁场关于中心轴没有切向分量。
式(4)右边第二项积分即为B→的径向分量By为
(6)
令sin φ=2sin2θ-1,可得
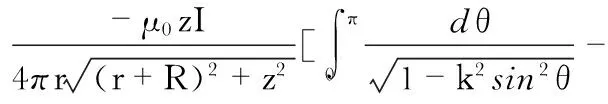
(7)
式(4)右边第三项即为B→的轴向分量Bz为
(8)
式(7)、式(8)的组合为圆环线圈的磁场强度公式。螺旋线圈的磁场强度为各个圆环线圈磁场强度的叠加,即对单个圆环线圈的半径R从r1到r2的积分。
螺旋线圈磁场强度By,Bz可表示为
(9)
(10)
式(9)、式(10)中,K(k),E(k)为第一类和第二类全椭圆积分,I为电流大小,μ0为真空磁导率,z为z轴方向的坐标,r1,r2是螺旋线圈的内、外径。
由于各个螺旋线圈磁场之间互不影响,因此,式(9)、式(10)为柔性涡流阵列传感器阵列单元线圈的磁场强度公式。
3 柔性涡流阵列传感器磁场强度仿真分析
采用Matlab软件,对柔性涡流阵列单元线圈磁场强度进行仿真分析。其相关参数设置如下:螺旋线圈的内径r1=4 mm,外径r2=10 mm,线圈径宽为0.2 mm,线圈之间间隙b=1 mm,电流I=0.8 A。阵列单元线圈磁场强度径向分量By和轴向分量Bz随坐标y,z的变化如图3所示,By和Bz与电流I的关系如图4所示,By和Bz与螺旋线圈间隙大小关系如图5所示。

图3 By和Bz径向分布和轴向分布Fig 3 Radial and axial distribution of By and Bz

图4 By和Bz与电流关系(I=0.4 A)Fig 4 Relationship between By,Bz and current(I=0.4 A)
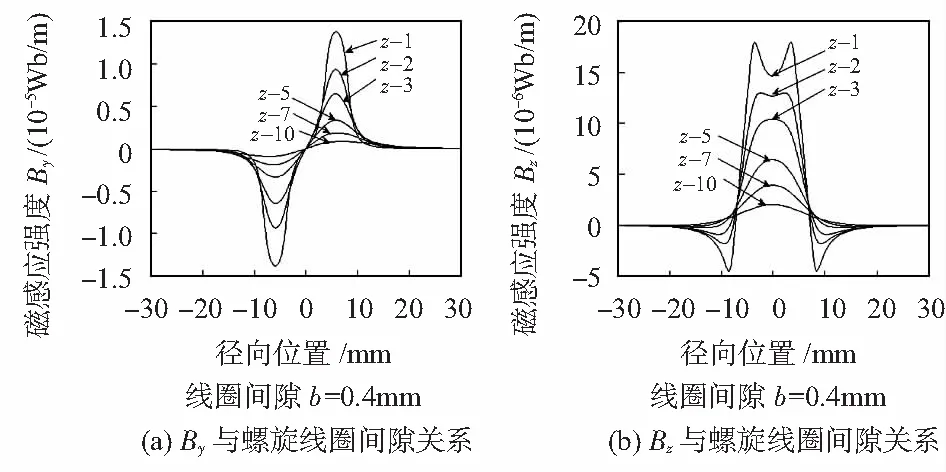
图5 By和Bz与螺旋线圈间隙关系Fig 5 Relationship between By,Bz and gap of spiral coil
由图3(a)可知,单个阵列单元线圈的磁场强度的径向分量By,在中心处磁场强度为0,随着y的增大先增大再减小,By在线圈外围最大;由图3(b)可知,By在轴向方向随着z的增大,先增大再减小,在中心附近达到最大值。
由图3(c)可知,z=1,2,这二条曲线的轴向分量Bz随着y的增大,先逐渐增大再减小,在中心点附近达到最大值。z=3,5,7,10这四条曲线,在中心点处达到最大值,随着y的增大,向外一直在减小。由图3(d)可知,在中心点处达到最大值,随着z的增大逐渐减小(曲线y=1只是方向相反而已)。
由图4与图3(a),3(c)比较可知,径向分量By和轴向分量Bz的磁场强度随电流I的增大而增大,且z较小的曲线增大的幅度较大。
由图5与图3(a),3(c)可知,By,Bz的值与螺旋线圈之间间隙b成反比,b增大时,By,Bz的值减小。
从上述分析可得:
1)柔性阵列单元线圈磁场强度径向分量By在螺旋线圈中心位置磁场强度为0,在边缘y=8 mm附近磁场强度达到最大;轴向分量Bz在线圈中心处磁场强度最大,随y的增大逐渐减小。由图3(a)可知,在y=10 mm附近磁场强度还存在,且随着y的增加一直在减小,直到y=20 mm处才消失。在螺旋线圈边缘也有磁场存在即边缘效应,且边缘效应范围在y=10~20 mm之间。由图3(a)和图3(c)可知,在径向y=20 mm处,By和Bz的磁场强度都为0,所以,在阵列单元布局时为了防止阵列单元线圈磁场的相互影响,相邻阵列单元之间间距至少为外径的2倍。
2)由图3(a)可知,z=1 mm这条曲线的磁场强度变化最大,也是磁场强度最大的曲线;而z=10 mm,这条曲线随着y的增大,By变化不大。这是因为z=10 mm的曲线与螺旋线圈距离较远,磁场强度衰减较快,磁场强度很小,这就是提离效应,本文设计的传感器提离距离为10 mm。
3)柔性阵列单元线圈磁场强度与电流大小有关,随着电流的增大而增大,可以适当增大电流来提高磁场强度;柔性阵列单元线圈磁场强度与线圈间隙有关,间隙越小,磁场强度越大,可适当地减小间隙来增大磁场强度。
4 结束语
本文论述了由6个阵列单元组成的柔性涡流阵列传感器,对其阵列单元磁场强度进行计算研究,探索了阵列单元磁场强度与电流、线圈间隙的关系。结果表明:柔性涡流阵列传感器阵列单元线圈的提离效应在z=10 mm处,边缘效应范围在y=10~20 mm处;柔性阵列单元磁场强度可以通过适当地增大电流或减小线圈之间的间隙等手段来增大磁场强度,对柔性涡流阵列传感器的发展起到一定的作用。
[1] 杨志坤,郑勤红,解福瑶,等.发展中的涡流无损检测技术[J].云南师范大学学报,1997,17(4):58-63.
[2] 丁 华,何宇廷,焦胜博,等.基于涡流阵列传感器的金属结构裂纹监测[J].北京航空航天大学学报,2012,38(12):1629-1633.
[3] 徐 瑶,潘孟春,田武刚,等.用于应力监测的新型平面柔性涡流传感器[J].测试技术学报,2012,26(4):354-362.
[4] 唐 莺,赵建强,胡恒江,等.平面柔性涡流传感器工作频率影响分析与验证[J].仪表技术与传感器,2015 (8):4-6.
[5] Hardy L,Billat A,Villermain-Lecolier G.Flat eddy-current matrix sensor for detecting metallic objects[J].Sensors and Actuators:A,1991,29(1):13-19.
[6] 杜金强,何宇廷,李培源.矩形柔性涡流阵列传感器裂纹检测研究[J].传感器与微系统,2014,33(5):12-17.
[7] 陈祥林,丁天怀,黄毅平.新型接近式柔性电涡流阵列传感器系统[J].机械工程学报,2006,42(8):150-153.
[8] 丁天怀,陈祥林.电涡流传感器阵列测试技术[J].测试技术学报,2006,20(1):1-5.
[9] Uesaka M,Hakuta K,Miya K,et al.Eddy-current testing by flexible micro-loop magnetic sensor array[J].IEEE Transactions on Magnetics,1998,34(4):2287-2297.
[10] Ding T H,Chen X L,Huang Y P.Ultra-thin flexible eddy current sensor array for gap measurements[J].Tsinghua Science &Technology,2004,9(6):667-671.
Magnetic field computational analysis of flexible eddy current array sensor*
CAO Qing-song,BI Bin-jie,ZHOU Ji-hui
(School of Mechanical and Electrical Engineering,East China Jiaotong University,Nanchang 330013,China)
A flexible eddy current array sensor consists of six array units(spiral coil)is designed,establish electromagnetic field model for flexible eddy current array units based on electromagnetic field theory,the magnetic field strength formula in radial and axial of flexible array unit coil are derived,simulation analysis on relationship between array unit coil magnetic field strength and current,coil gap,inner and outer diameters and other parameters,which have a certain reference value for development of flexible eddy current array sensor.
flexible eddy current array sensor;crack detection;magnetic field intensity;spiral coil
10.13873/J.1000—9787(2016)11—0006—03
TP 212.1
A
1000—9787(2016)11—0006—03
2016—01—07
江西省自然科学基金资助项目(2013BAB216029)
曹青松(1978-),男,安徽无为人,博士,副教授,主要从事测控技术与仪器研究工作。

