挠性加速度计石英摆片的微运动仿真分析*

连德浩，李 强，孙 飞，陈雪冬

(1.西南科技大学 信息工程学院，四川 绵阳 621900；2.中国工程物理研究院 电子工程研究所，四川 绵阳 621010)



挠性加速度计石英摆片的微运动仿真分析*

连德浩1，李 强1，孙 飞1，陈雪冬2

(1.西南科技大学 信息工程学院，四川 绵阳 621900；2.中国工程物理研究院 电子工程研究所，四川 绵阳 621010)

加速度计石英摆片的微运动仿真分析可以获取帮助提高石英挠性加速度计生产质量的技术手段和途径。从加速度计石英摆片的物理模型入手，用有限元方法对摆式加速度计的关键部件石英摆片进行静力计算与模态分析，直观地显示了石英摆片结构的应力场与形变场，获得了各阶自然频率和阵型。结果表明：采用有限元分析的方法能够辅助提高加速计的性能。

石英挠性加速度计； 有限元； 模态分析

0 引 言

石英挠性加速度计是一种经典的高精度机械摆式加速度计，因其具有结构简单、体积小、功耗低、灵敏度高等优点，在地质钻探、海洋调查等多个领域具备广泛的应用，特别是作为惯性导航设备，其性能直接影响整个系统的测量精度与稳定性[1]。

石英挠性加速度计对摆片装配的对中性要求极高，以保证摆片平稳。挠性加速度计结构设计中所选石英材料的脆性、加工工艺过程中摆片质量分布不均以及工作过程中自身发热等问题均会造成摆片的不对中缺陷，都会导致石英挠性加速度计的摆片失稳问题。因此,针对此种问题对石英摆片进行微运动仿真分析就具有重要的现实意义。

在现有的研究基础上，本文针对石英挠性加速度计，利用丹麦B&K 3629传感器振动校准系统，运用有限元分析软件对部件的应力、位移、应变和力等参量由于稳态外载的作用发生改变进行静力分析。同时为确定所研究摆片的振动特性对其进行模态分析，并据此来改善加速度计的性能。

1 加速度计组件的工作原理与力学分析

1.1 加速度计工作原理

根据石英挠性加速度计的结构资料描述，主要包含摆组件、挠性杆、力矩器、反馈回路等组成部件[2]。当有加速度作用时，由挠性摆和力矩器线圈组成的检测质量块将由于惯性作用相对平衡位置发生微小偏转，从而产生相应的惯性力；同时，差动电容器间距的改变将导致电容量发生变化，伺服放大器电路将检测这一变化并转换为相应的输出电信号，电流信号被馈送到处于恒定磁场中的力矩器而产生反馈力，与惯性力相平衡，使摆片重新恢复到平衡位置。

1.2 石英摆片力学分析

力学分析方法主要是解析法与数值法。由于实际结构形状和所受载荷比较复杂，大多用解析法比较困难，因而数值法得到广泛运用。本文从加速度计工作状态出发，针对正常与异常两种情况，做了详细的分析讨论[3]。

1)正常工作情况下，石英摆片处于上下平稳运动的模式，如图1、图2所示。

图1 正常加速度计摆片运动模型示意图Fig 1 Diagram of Normal accelerometer pendulum motion model

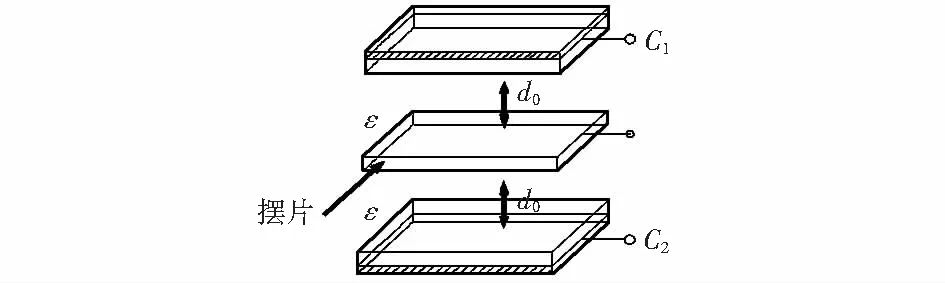
图2 加速度计摆组件三维工作模型示意图Fig 2 Working model diagram of accelerometer pendulum assembly

初始状态时的极板间距描述为d0，对应的初始电容量为C0，即为

(1)

式中 ζ为极板间介质的介电常数，S 为极板的遮盖面积[4]。当摆片上下平动时，C1，C2成差动变化，即一个电容量增加，另一个电容量减小，动极片向上移动Δd,则电容C1和C2将产生如下变化

(2)

(3)

若Δd很小，将以上两式按级数展开并相减可得到Δd与ΔC的关系为

(4)

综上所述形成一个循环，电场力作用引起石英摆片平动导致距离Δd发生变化，进而使ΔC变化，再反过来影响电场力。

2)异常工作情况下，石英挠性加速度计可能出现扭摆、随机摆动的情况，如图3、图4所示。同时给出扭摆的受力分析图，如图5所示。

图3 异常加速计绕点扭摆工作图Fig 3 Working diagram of abnormal accelerometer torsion around point

图4 异常加速计绕轴扭摆工作图Fig 4 Working diagram of abnormal accelerometer torsion around axis

图5 异常加速计摆片受力分析图Fig 5 Force analysis diagram of abnormal accelerometer pendulum

图3中，摆片围绕左端固定支点上下扭动，接下来摆片将向上扭动，摆片受到向上的加速度，图中Ft为摆片受到的轴向拉力，Fc为支撑摆受到的轴向压力，G为摆片受到的重力，ma为摆片受到的惯性力。具体分析如下

(5)

∑M=0⟹(m·a)·l1-Ft·l2=0

(6)

(7)

由以上两式，可以得出力与加速度a的关系式，再由摆片受到的振动偏微分方程[5,6]

(8)

式中 E为弹性模量；J为梁的横截面在弯曲方向的惯性矩，大小为hw3/12；y为挠度，x为轴向坐标，F为梁受到的轴向力，ρ为材料密度；A为横截面积，大小为hw；t为时间。设原点在振梁左端，由于梁是两端固定，故边界条件为

y(0)=y(l)=0

(9)

(10)

依据边界条件解微分方程即可获得频率与轴向力的关系，可得

(11)

式中

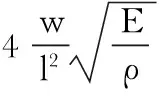
(12)

由轴向力与加速度的关系式和轴向力与频率的关系式可以得到频率与加速度的关系式。

图4中,摆片围绕某一固定轴做运动，出现扭摆现象。摆片围绕中心轴线方向转动，摆片距离上下固定极板的距离在以中心轴线分成的两块区域是完全对称的，即在中心轴线一侧上表面距离减少，下表面距离增加；中心轴线另一侧则是上表面距离增加，下表面距离减少。对比正常加速度计工作情况，极板的遮盖面积S根据翻转角度而变化，在0°时最大，在90°时最小，分析可得到一个关于ΔS，Δd与ΔC的关系。电场力的作用引起距离和面积的改变，进而使ΔC发生变化，再反过来影响电场力。

2 有限元分析

有限元法是把连续的几何结构离散成有限个单元,其过程为先建立等效有限元模型,定义单元类型和材料性能参数,划分网格,施加约束条件和载荷,求解并查看结果。

2.1 有限元模型建立

本文直接在有限元分析软件(ANSYS)里建立有限元模型，然后定义单元类型和材料属性。在建模的过程中，本文设定了有限元单元类型为20节点的单元SOLID97(石英摆片)，8节点的单元SOLID186(挠性支撑梁)，8节点的单元SOLID185(铝合金骨架)[7]。采用实体建模的方法一方面可以简化数据的处理，另一方面可以方便有效地进行网格划分[8]。

本文中，石英摆片的密度为2.8 g/cm3，泊松比为0.17，杨氏模量为7.5×1010Pa；挠性支撑梁的密度为3 g/cm3，泊松比为0.3，杨氏模量为2×1011Pa；铝合金骨架的密度为5 g/cm3，泊松比为0.3，杨氏模量为2×1011Pa。划分网格采用自适应网格划分的方法，划分网格前要匹配石英挠性加速度计各组件单元类型和材料属性，然后赋予每个组件相对应的单元和材料属性进行网格划分。有限元模型和网格划分模型如图6、图7。

图6 有限元模型图Fig 6 Finite element model

图7 网格划分模型Fig 7 Meshing model

2.2 模态分析

模态分析是获取石英挠性加速度计摆片自然频率和阵型的主要方法。自然频率和振型是动态载荷结构设计中的重要参数[9]。模态分析的作用是使结构设计避免共振或按特定频率振动,还可以了解结构对于不同类型动力载荷的响应[10]。

由于模态对系统的贡献是随着阶数增加而减少的，太高阶模态的作用基本可以忽略，因此本文只取了前五阶模态的仿真结果。同时也给出了前五阶模态的阵型图,如图8。

图8 前五阶模态的阵型Fig 8 Formation of the first 5 order modal

阵型阶次频率阵型描述113.226绕z轴摆动213.009绕y轴转动330.524挠性杆波动434.496绕x轴摆动545.084绕z轴摆动

从表1中可以看出,结构随着阵型阶次的升高频率整体呈现上升的趋势，一阶模态的振动频率要略低于其他阶的振动频率。结构的振型主要表现为一阶模态，二阶模态的阵型，即绕z轴的摆动和绕y轴的转动。实验所选用的双挠性杆加速度计设计一方面减小了系统的角刚度,另一方面也减小了结构绕y轴的转动。同时,在确保系统精度的前提下,结构绕y轴的转动也可以通过减小挠性杆的厚度h来抑制。

模态分析对于结构设计的好处主要表现在以下两个方面:1)有利于改善加速度计的自然频率,有效防止结构与环境发生共振；2)通过调整挠性杆厚度,使结构其它各阶模态的频率远离加速度计的主要模态的频率。

2.3 静力分析

静力分析主要用来分析固定不变载荷作用下的结构效应,即稳态外载荷所引起的系统或部件的位移、应力、应变和作用力。静力分析的主要步骤是:建立模型、施加载荷、求解和检查结果[11]。静力分析的主要结果就是应力场分布和变形场分布[12]。石英挠性加速度计x轴，y轴，z轴的位移云图9所示。石英挠性加速度计应力分析云图10所示。

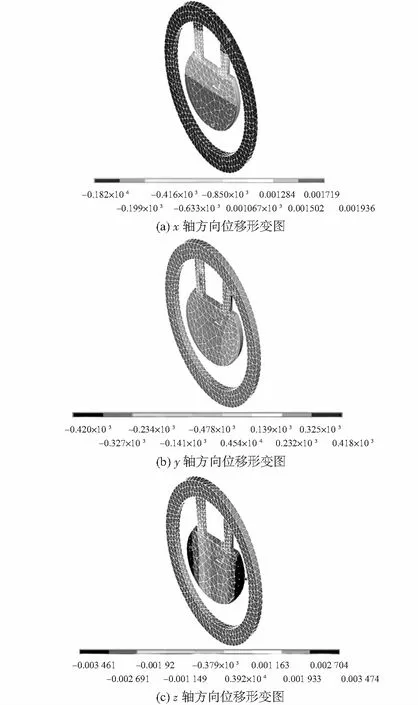
图9 三个方向位移形变图Fig 9 Diagram of three direction dispacement deformation

图10 一阶模态等效应力云图Fig 10 Equivalent stress cloud chart one order modal

从静力分析可得出两个挠性杆的端部受到的应力最大，图中显示为40.000 45 MPa，知道石英的理论极限为80 MPa，当超过这个极限时，石英挠性杆就会断裂。要想使石英摆片获得更高的灵敏度和精度，就要提高石英摆片的挠度。与此同时，也会带来负面的效果，挠度越大，挠性杆越容易断裂。所以要综合考虑这些方面的情况，在低于极限应力条件的情况下，更有效地提高其精度和灵敏度。

3 结 论

为获得石英挠性加速度计的微运动仿真分析，对加速度计做了多方向振动试验，深刻了解加速度计的运动机理，借助有限元分析软件ANSYS对石英摆片进行了有限元模型的搭建，并做了模态分析与静力计算，得到了石英摆片的自然频率和相应阵型、位移特性、应力特性。这些结果作为参考，可以有效地避免石英摆片在工作状况下的断裂，另一方面也验证了结构设计的正确性。

[1] 陈雪冬，张 德.石英挠性加速度计网络化自主测试系统[J].传感器与微系统，2014,33(8):2-3.

[2] 延 波.RIMU计划的125 g石英挠性加速度计的发展[J].导航与控制，2005，18(4):39-44.

[3] 王春爱,蔡体菁.挠性加速度计石英摆片的力学分析[J].舰船电子工程,2009(3):56-60.

[4] 徐 鹏,祖 静,林祖森.微加速度计的力学分析[J].传感器技术,2002,21(6):62-64.

[5] 李 安.石英挠性加速度计关键技术研究[D].杭州:杭州电子科技大学,2011：25-28.

[6] 李 晶,樊尚春.谐振式加速度计模型分析与仿真[J].传感器与微系统,2013,32(6):33-35.

[7] 李 安,张云电.石英挠性加速度计摆片组件的应力分析[J].机电工程,2010,27(10):1-4.

[8] 杨 挺,杨贵玉,李庆丰.石英振梁加速度计静态输入输出特性[J].中国惯性技术学报,2014，22(3):386-389.

[9] 何江波,谢 进.具有不对称弹性梁的梳状维嘉速度计的结构变形分析[J].机械，2011,38(10)：5-8.

[10] 董景新,张自然.挠性摆式微硅加速度计的模态分析[J].清华大学学报:自然科学版,1998,38(11):16-18.

[11] 寇剑菊,苏 伟.叉指式加速度计的一种仿真法分析[J].传感器技术,2003,22(6):27-29.

[12] 姜德生,陈大雄,粱 磊.ANSYS 在光纤 Bragg光栅加速度计设计中的应用[J].传感器技术,2004,23(11):75-77.

Micro motion simulation analysis of quartz pendulum in flexible accelerometer*

LIAN De-hao1,LI Qiang1，SUN Fei1，CHEN Xue-dong2

(1.School of Information Engineering，Southwest University of Science and Technology， Mianyang 621900,China;2.Institute of Electronic Engineering,China Academy of Engineering Physics,Mianyang 621010,China)

The micro motion simulation analysis of accelerometer quartz pendulum can get technical method and approach to improve production quality of quartz flexible accelerometer.Starting with the research of physical model of accelerometer quartz pendulum,static calculation and modal analysis on key component quartz pendulum are carried out through the finite element method,visually display stress field and deformation field of the structure of quartz pendulum,and gain natural frequency in different orders and formation.The results indicate that the finite element method can improve the performance of accelerometer.

quartz flexible accelerometer;finite element;model analysis

10.13873/J.1000—9787(2016)11—0015—04

2016—04—29

西南科技大学研究生创新基金资助项目(15YCX124)

TP 391

A

1000—9787(2016)11—0015—04

连德浩(1991-)，男，山西晋城人，硕士研究生，研究方向为石英挠性加速度计状态建模与仿真分析。