二维超声波风速风向传感器风向信号修正方法*

李静海，曾 明，张小内

(天津大学 电气与自动化工程学院 机器人与自主系统研究所，天津 300072)



二维超声波风速风向传感器风向信号修正方法*

李静海，曾 明，张小内

(天津大学 电气与自动化工程学院 机器人与自主系统研究所，天津 300072)

针对二维超声波风速风向传感器输出的风向信号普遍存在风向角瞬变的问题，研究了产生风向角瞬变现象的原因，并提出了一种基于幅值—符号分解的风向修正算法。理论分析和实验结果表明：风向信号中的风向角瞬变是由传感器的量程限制造成的；基于幅值—符号分解的风向修正算法能在不改变风向角所表征的方位特征的前提下消除风向角瞬变。

风向信号； 二维超声波风速风向传感器； 幅值—符号分解； 风向修正

0 引 言

超声波风速风向传感器由于其反应速度快、测量精度高、维护使用方便等优点，在工业领域和科学研究中得到了广泛的应用[1]。二维超声波风速风向传感器主要利用两对垂直放置的超声波换能器接收端和发送端之间的超声波频率差别来计算风速和风向[2]，传感器输出风速(m/s)和风向(°)时间序列。在分析由二维超声波风速风向传感器测得的风向信号时，风向数据中普遍存在风向角瞬变现象，即在很短的时间内风向角出现极为剧烈且幅度很大的波动。风向角瞬变时段的风向信号波动特性与其他时段明显不同，只有深入了解出现风向角瞬变现象的原因，才能判断出这种现象是否会对后续风向信号波动分析产生影响，如果有不利影响，还应采用适当的方法对风向信号做合理的修正，然而目前尚未发现有文献对该现象做过探究。

本文首先探讨了二维超声波风速风向传感器输出的风向信号中出现风向角瞬变现象的原因，然后提出了基于幅值—符号分解的消除风向角瞬变的风向修正算法，最后通过统计方法和风玫瑰图对实验效果进行了验证。研究结果将为实测风向数据的处理和分析提供新的理论依据。

1 实验数据测量

利用二维超声波风速风向传感器(WindSonic)测量室外空旷场地内的风向数据，该传感器的风向量程为[-180°,180°]，分辨率为1°。在测量过程中，传感器高度为0.3 m，采样频率为4 Hz。进行多次实验后，选取具有代表性的1 h的风向时间序列WD，时间序列长度为14 400，如图1(a)所示。取其中波动较为剧烈的时段(即第10 000个采样点到第11 000个采样点，如图1(a)灰底标识区段)，将其放大并绘制在图1(b)中。

2 幅值—符号分解基本原理

幅值—符号分解是Ashkenazy Y等人[3]提出的一种主要用于波动特性分析的信号分解方法，能将一个复杂信号分解为幅值序列和符号序列，已在信号分析领域得到了广泛应用[4～6]。该方法主要包括两个步骤：

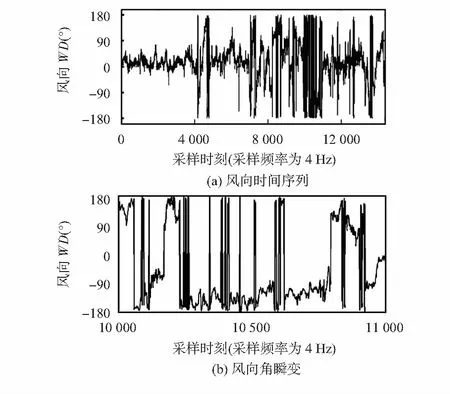
图1 风向时间序列Fig 1 Wind direction time sequence

1)给定一个时间序列{xi}(i=1,2,…,N)，求出它的增量序列{Δxi}，其中，Δxi=xi+1-xi(i=1,2,…,N-1)。

2)将增量序列分解为幅值序列和符号序列，对增量序列每个元素取绝对值就得到幅值序列{|Δxi|}，取增量序列每个元素的符号即得到符号序列{sgn(Δxi)}。

3 风向信号中出现风向角瞬变的原因

从图1看出，风向信号从第4 000个采样点开始频繁出现风向角大幅波动。通过大量的实验，发现二维超声波风速风向传感器的输出风向信号出现风向角短时大幅波动的情况普遍存在。为了研究出现这种风向角瞬变的原因，采用幅值—符号分解法。计算出图1(a)中风向时间序列的增量序列ΔWD、幅值序列|ΔWD|和符号序列sgn(WD)，分别如图2(a)、图2(b)和图2(c)所示。为了显示清晰，符号序列仅画出了前100个点。

图2 风向时间序列的幅值—符号分解Fig 2 Magnitude/sign decomposition of wind direction time sequence

从图2可以看出，风向增量序列和幅值序列在某些时段出现了尖峰值，尖峰值已经远远超出了平均幅值。首先，设定波动阈值为180°，当幅值|ΔWD|>180°时，认为发生了风向角瞬变。设定波动阈值为180°的原因在于在极坐标系下，对于同样的波动效果，存在(0°,180°)和(180°,360°)内两个等效的波动量，180°是极坐标系下的中间角度，例如顺时针波动30°与逆时针波动330°是等效的。然后，统计出在所有采样时刻内的风向角增量和相应时刻的风向角，如图3所示。在图3中，低于180°的风向角增量用‘◇’表示，对应时刻的风向角用 ‘★’表示；高于180°的风向角增量用‘●’表示，对应时刻的风向角用‘□’表示。

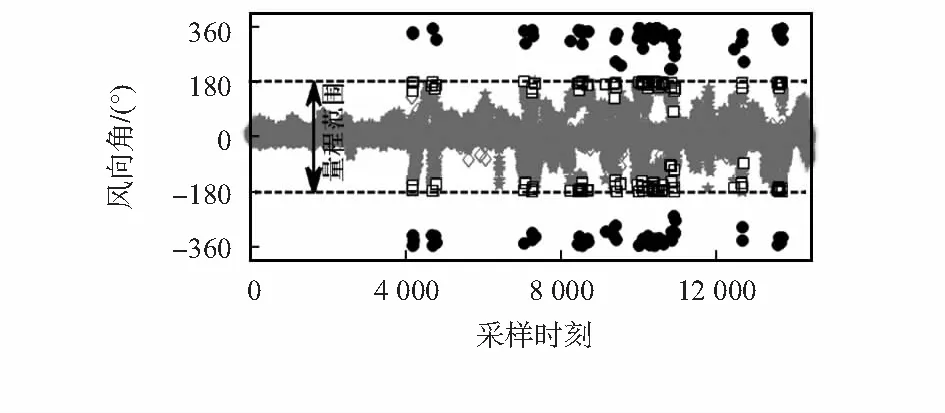
图3 风向角增量和相应时刻的风向角统计Fig 3 Statistics of wind direction increment and corresponding wind direction angle

从图3可以看出，大部分时刻的风向角增量在180°以内，风向角增量超过180°(●)的时刻只占所有采样时刻中的很小一部分(比例低于0.86 %)，发生大幅波动时刻的风向角(□)均在量程极值附近。根据上述幅值—符号分析可以肯定，风向信号中的风向角瞬变这一现象与传感器的量程极值有关。

二维超声波风速风向传感器的风向角量程为[-180°,180°]，在测量风向信号时，当风向角增加到180°以后，如果再往上增加，由于量程的限制，传感器输出只能从负角度方向取值。例如:某一时刻风向角为178°，相邻的下一时刻应该为185°，在极坐标系下角度变化量仅为7°，但185°已超出了传感器量程范围，因此，传感器只能输出一个在极坐标系下与185°等效的-175°，这样的输出结果使得角度变化量不再是7°，而是 -353°，因此，便出现了图 1中风向角在某些时刻变化幅度极大的情况。当角度减小到-180°以下也是类似的。如果风向角总是在极值附近，那么风向角大幅波动将持续存在。由此可知，风向角瞬变这一现象是由传感器量程所造成的。

由传感器量程限制而造成的风向角瞬变现象在一定程度上掩盖了真实的角度变化量，这可能会对后续的风向波动特性分析造成不利影响，因此，需要采用合适的方法来消除风向信号中的风向角瞬变。

4 消除风向角瞬变的方法

当风向角在一个较小的范围内波动时，可以通过调整传感器的安装方向来避免风向角的瞬变，即先估计测量区域的主风方向，然后将传感器量程中间值(即0°)调整到主风方向上。此时绝大部分风向角都围绕主风向附近波动，极少会靠近量程极值处，因而可以避免测得的风向信号出现风向角瞬变。然而对于波动特性更为复杂的风场，风向角遍布量程范围内的所有角度，利用调整传感器的安装方向的方法就无法避免和消除风向角瞬变。

针对上述问题，本文提出了一种基于幅值—符号分解的风向修正方法，即在不对传感器进行调整的情况下，通过对测得风向信号进行修正来消除风向角瞬变现象，并确保风向角所表征的方位特征不变。该算法包括如下四个步骤：

1)利用幅值—符号分析法：将风向信号{WDi}(i=1,2,…,N)分解为幅值序列{|ΔWDi|}和符号序列{sgn(WDi)}。

2)对幅值符号序列进行修正：若在时刻i的幅值|ΔWDi|>180°，则将|ΔWDi|修正为|ΔWDi|corr=360°-|ΔWDi|，将该时刻的符号值sgn(WDi)修正为sgn(WDi)corr=-1×sgn(WDi)；若|ΔWDi|≤180°，则|ΔWDi|corr=|ΔWDi|，sgn(WDi)corr=sgn(WDi)。

3)基于修正后的幅值序列{|ΔWDi|corr}和符号序列{sgn(WDi)corr}构造增量序列{ΔWDi}corr，即ΔWDi|corr=sgn(WDi)|corr×(|ΔWDi|)|corr。

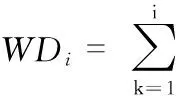
该方法易于在数据处理中实现并且无需对传感器进行调整，修正前与修正后的风向角在极坐标系下是等效的。由于在(2)步中限制了风向波动幅值，因而能消除风向角的大幅波动；由于取消了角度范围的限制，所以,修正后的风向角可能会超出区间[-180°,180°] 。

5 实验测试

采用第4节的方法用对图1(b)所示的第10 000～11 000个采样点的风向时间序列进行修正。修正前后的风向时间序列如图4所示。统计出修正前和修正后在的风向角增量和相应时刻的风向角，如图5(a)和图5(b)所示，其中低于180°的风向角增量用‘◇’表示，对应时刻的风向角用‘★’表示；高于180°的风向角增量用‘●’表示，对应时刻的风向角用‘□’表示。结合对应时刻的风速值，作出修正前后的风玫瑰图，分别如图6(a)和图6(b)所示。

图4 修正前和修正后的风向时间序列Fig 4 Wind direction time sequence before and after correction

图5 风向角增量和相应时刻的风向角统计Fig 5 Wind direction angle increment and statistics of corresponding moment wind direction angle

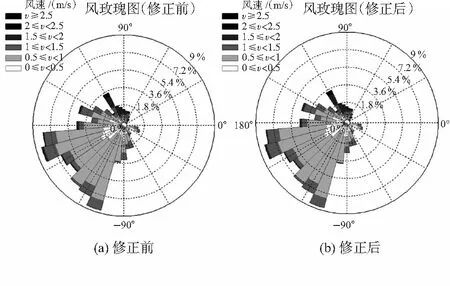
图6 风玫瑰图Fig 6 Wind rose

从图4可以看出，通过修正，明显能将风向信号中的大幅波动去除；从图5可以看出，修正后已没有超过180°的波动(●)，但有一部分风向角(★)超出区间[-180°,180°]；从图6可以看出，修正过程并不改变风玫瑰图。由此可知，本文提出的风向修正算法能在不影响风向信号所表征的方位特征的前提下，消除风向角瞬变现象，从而避免风向角瞬变对后续风向波动特性的分析造成不利影响，但修正后的风向角可能会超出传感器的量程限制范围。

6 结 论

本文探究了由二维超声波风速风向传感器测得的风向信号发生风向角瞬变现象的原因，证实了该现象是由传感器本身的量程限制造成的，并且会掩盖真实的角度变化量。为了避免风向角瞬变对后续风向信号波动特性分析造成不利影响，提出了基于幅值—符号分解的风向修正方法，该方法能在不改变风向角所表征的方位特征的前提下很好地消除传感器输出风向信号中存在的风向角瞬变现象。

[1] 张东明，曹晓钟，马尚昌.二维超声波风速风向传感器设计[J].传感器与微系统,2015,34(10):110-113.

[2] 闫 茹，蒋翠丽.浅谈风速风向传感器[J].内蒙古石油化工,2011(21):42.

[3] Ashkenazy Y,Ivanov P C,Havlin S,et al.Magnitude and sign correlations in heartbeat fluctuations[J].Physical Review Letters,2001,86(9):1900-1903.

[4] Ashkenazy Y,Havlin S,Ivanov P C,et al.Magnitude and sign scaling in power-law correlated time series[J].Physica A—Statistical Mechanics and its Applications,2003,323:19-41.

[5] Telesca L,Lapenna V.Magnitude and sign scaling in power-law correlated geoelectrical time series measured in southern ita-ly[J].Natural Hazards and Earth System Sciences,2004,4(5-6):669-677.

[6] Li Q,Fu Z,Yuan N,et al.Effects of non-stationarity on the magnitude and sign scaling in the multi-scale vertical velocity increment[J].Physica A—Statistical Mechanics and its Applications,2014,410:9-16.

Correction method for wind direction signal measured by 2D ultrasonic anemometer*

LI Jing-hai,ZENG Ming,ZHANG Xiao-nei

(School of Electrical Engineering and Automation,Institute of Robotics and Autonomous Systems, Tianjin University,Tianjin 300072,China)

Aiming at problem that wind angle transient is common in wind signal for 2D ultrasonic anemometer,causes of this problem is studied,and a correction algorithm based on magnitude/sign decomposition is proposed.Theoretical analysis and experimental results show that the wind angle transient is arised by range limits of sensor,and the correction algorithm based on magnitude/sign decomposition can eliminate this problem without changing orientative feature represented by wind angle.

wind direction signal;2D ultrasonic anemometer;magnitude-sign decomposition;wind direction correction

10.13873/J.1000—9787(2016)11—0012—03

2016—01—08

国家自然科学基金资助项目(61271321,61573253,61401303)

TP 212.9

A

1000—9787(2016)11—0012—03

李静海(1987-)，男，白族，云南大理人，硕士研究生，研究方向为复杂动态气流环境下机器人气体泄漏源定位和超声波风速风向传感器。