“用数对确定位置”学习体验案例

蒋玲玲 郁 军

（1.贵阳市第一实验小学，贵州 贵阳 550081；2.南明区教师学习与资源中心， 贵州 贵阳 550000）

“用数对确定位置”学习体验案例

蒋玲玲1郁 军2

（1.贵阳市第一实验小学，贵州 贵阳 550081；2.南明区教师学习与资源中心， 贵州 贵阳 550000）

教师引导学生在生活的情境中认识列、行的含义，并利用行列确定位置，进而抽象出用有序数对描述平面上点的位置。学生在逐次“数学化”的活动过程中，体验数形结合的思想，发展数学推理与运用的意识。

数学化；数形结合；学习体验

一、教学设计

1.课时目标

（1）引导学生在教室座位的情境中认识列、行的含义，知道确定第几列、第几行的规则，会用数对表示具体情境中的物体的位置，进而用有序数对描述方格图上（平面上）点的位置。

（2）引导学生感受数对与生活实际的联系，在逐次“数学化”的抽象过程中，逐步掌握用数对确定位置的方法，初步体验数形结合的思想。

核心素养：数形结合思想，有序数对与位置（点）的一一对应。

2.重、难点与核心问题

重点：根据具体情境，应用数对确定点的位置。

难点：理解位置（点）与数对表示的有序性、对应性。

核心问题：怎样在平面上确定点的位置？

3.设计思路

用教室座位图作学习情境导入学习主题（为什么要学习确定位置？）——新课教学（怎样确定位置？）——列、行的认识（已有经验的提升）——引导学生在“做数学”中体验数对形成过程（初次数学化）：制造设计符号的需要；在交流中统一确定位置的符号——数对；初步练习用数对确定位置——多层练习，巩固运用新知识，实现“数学化”（二次数学化）——座位里的数对、拓展延伸。

二、教学过程

1.片段一：情境激趣引入——用课件展示教室座位图

师（出示座位图）：这是五年级某一个班的座位图，他们的班长叫小军，你知道他是哪一个吗？

生：不知道！

师：那我就给点提示吧。他呀，在第4组。

生：第4组第3个。

师：猜对了！他就在第4组第3个（见图1），

图1

这个位置还可以怎么说？

生1：第3排第4个。

生2：第3排倒数第3个。

师：光说第几组或第几排能确定小军位置吗？

生：不能。还得说清楚是在第几组第几个，或者第几排第几个。

师：对！既然第几组第几个或者第几排第几个就能确定小军位置了，那我们还研究什么呢？怎样才能更准确、简明地说出小军的位置呢？今天我们就一起来探究一下“确定位置”。

评析：在让学生用以前学过的知识猜班长小军的位置时，不仅能唤起以前所学习的知识，激发学习兴趣，也在让学生用以前知识描述位置时，感受学生说法很多，容易产生误导，从而产生学习规范语言的需要。但老师过渡有点快，没有让学生感受到为什么还要研究的原因，而是老师直接说“由于说法太多，容易产生误导”。

2.片段二：对已有知识提升——理解确定座位以及点的位置的方法

师：（PPT显示字幕）在今天的确定位置中，会用到两个新的名词，引出：什么叫列？什么叫行？【板书：列 行】

生：竖排就叫做列。【板书：竖列】横排就叫做行。【板书：横行】

师:你能用手势比划比划吗？（学生指教室座位）其实，竖排（手势）就是我们以前说的——小组，【板书：（组）】横排（手势）就是我们以前说的——一排。【板书：（排）】

师：接着看，我们做出了一个什么约定？你认为怎么确定第几列和第几行？（学生边描述，边比划。）

评析：通过学生独自阅读，根据二年级学习确定第几组，第几排的知识，进行知识迁移，逐步理解确定第几列和第几行的数的顺序。这样做，一方面培养了学生独立学习的能力，另一方面，在学生描述与比划中，培养了学生的表达能力与丰富了学生的学习体验，加深对规则的理解。

师：我们来试一试！请同学们注意观察。第4列同学请起立；再请第3行同学起立。

师：谁站了两次。为什么他站了两次？

生：因为他既在第4列，又在第3行。

师：既在第4列，又在第3行的这个人有几个？

生：一个。

师：对！只有他一个。你看，抓住列数和行数就能准确确定位置，而且这个交叉点的位置是唯一的！

师：约定：先说列数，再说行数，他的位置就应该说成是——

生：第4列第3行。

师：你能用这样的说法来描述自己的位置吗？比如，我的位置在第4列第3行。谁来试试？

评析：请第4列和第3行同学起立，一方面巩固前一环节确定位置的方法，另一方面让学生理解抓住列数和行数即能确定交叉点的位置，体会位置的唯一性，同时也为后面把座位抽象成点的确定位置的方法做准备。

3.片段三：初次数学化——探索表示方法，写出“数对”

师：刚才说的这些点的位置，你能快速的记录下来吗？（学生拿出答题单，准备听写。）

师：停！怎么了？

生：写不下来，太快了。

师：你能不能找出一种更简单的方法来表示刚才我说的位置呢？我们就以第4列第3行为例，抓住其中重要的信息（4列和3行），请你想出一种更简单的方法来表示它！设计设计，写在答题单上。

师：我们来看看，这里我收集了几位同学设计的方法，这些方法是否合理呢，我们一起来探讨一下！

评析：在这个环节，学生设计的方法多种多样，教师选择3种有代表性的进行展示交流，指出第三种方法和数学家设计的是一样的，最终指出“数对”这一概念。教师没有直接告诉学生“数对”这一符号表示，而是充分发挥学生的学习主动性，在设计方法与比较交流过程中，理解符号设计的重要性与合理性，增强了学生思考的学习体验。

4.片段四：二次数学化——数对体验与平面直角坐标介绍

师：现在，老师要考考大家的反应能力！我直接报数对，请符合要求的同学迅速起立。数对（3，1），（3，2），（3，3），（3，4），（3，5）。

师：奇怪了，怎么就齐刷刷地站起来一队同学呢？

生：因为他们都是第3列的同学。

师：如果让你来说几个数对，你能让一队同学都站起来吗？谁来试试？

生：（2，1），（2，2），（2，3），（2，4），（2，5）。

师：真不错！说几个数对，站起来一队同学。但我觉得这还不算什么！要是我说，我只给一个数对，就可以请一队同学站起来，信吗？

生：信。

师：咱们试一试？【板书数对：（4，y）】符合要求的同学请站起来。

师：奇怪，我上面写数对（4，2）了没？那你干嘛站起来？

生：y是未知数，（4，y）可以表示第4列的所有同学。

师：4已经确定了是第4列的同学，而y是未知数，它表示任何一行，（4，y）可以表示第4列的所有的位置？瞧！老师厉害吧，出一个数对，就能请一队同学站起来。你能试一试吗？

生1：(5,y)。（交流体验。）

生2：(6,y)。（交流体验。）

师：刚才这两个数对都可能让一列同学站起来，那能请一行同学站起来吗？谁来试试？师（板书数对）：你为什么站起来？

生:(x,3)。（交流体验。）

师：说一个数对，能让一队同学站起来吗？可能让全班都站起来吗？

生：（x,y）。

师：为什么这个数对能让全班都站起来？

生1：因为x和y都是未知数，所以可能表示全班同学的位置。

生2：因为x表示所有可能的列数，y表示所有可能的行数。

师：x表示所有的列数，y表示所有的行数，它们可以任意组合，所以能代表班上任何一个同学的位置！

师：字母表示任何数，（板书数对：（x，x））也能让全班站起来喽！你怎么看？

生：不能表示全班同学的座位。它只表示列数和行数相同的座位。

师:当x等于1时，是数对（1,1）（板书）谁站起来？当x等于2呢？当x等于3呢等于4？等于5？不是说字母可以表示任何数吗？怎么不全班都站起来呢？

评析：学生的活动兴趣很高，极大多数同学都能参与有效的活动中，在站立、争论、疑、论驳中，充分体会字母表示的数对的含义，再一次将学生的学习主动性和学习体验感推向高潮。但是，在教学中发现五年级的学生对于用数对（x,y）表示全班同学的位置，理解上存在一定的困难，因此，这个地方最好留给学生课后去思考。

师：其实，除了教室里同学们的座位可以用数对来表示，平面图上的点也可以用数对来表示。

师：老师把之前的点子图给它加上横线和竖线还有必要的数字，请看，变成了什么？

生1：棋盘。

生2：方格图。

师：变化后，你们觉得有什么优点？

生1：这样表示更简单了。

生2：这样比刚才更清楚了。

师：指着原点：这个位置在哪里？

生：第0列第0行。

师：用数对怎么表示？

生：（0,0）。

师：班长小军的位置用数对表示是（4，3）。你能在方格中找到他的位置吗？（任意指几个点）那这一个点的位置用数对表示为？

师：判断很准确！接着来看一看！（课件出示动态演示缩放图，突出点的位置，第二象限）如果这个点在这儿（见图2），你还能用数对表示它的位置吗？

图1

生1：加方格。

生2：加数字。

师：怎么加？加什么数字？

生：负数。

师：太棒了！往相反方向添加了负数，再沿着原来方格的边线，反向延长，现在你能用数对表示这个点的位置吗？（见图3）

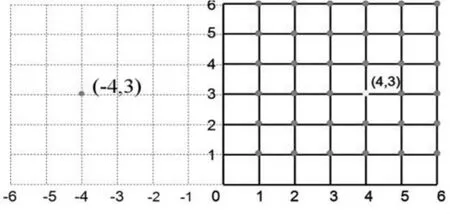
图3

生：（-4,3）。

师：负数都派上用场了，可别小看这一个小小的突破。有了负数的加盟，我们还能用数对来表示这个点的位置吗？怎么办？

生：加数字和方格。

评析：这一环节的设计，为接下来展示平面直角坐标做准备，也让学生对这一概念有了初步了认识。教学完后反思，对于小学五年级的学生来说，是否讲到第二象限就够了，至于第三象限和第四象限点的位置的问题，应该留给学生下去思考。

5.片段五：人文拓展——发明者笛卡儿的介绍，其他领域的运用

师：这节课，我们学习了用什么方法确定位置？

生：用数对的方法确定位置。

师：学习数对，我不得不提到一个人，著名数学家——笛卡尔。

师：笛卡儿这种献身数学的决心和毅力是值得我们每个人学习的。其实，在刚才的学习过程中，我已经看到了同学们探究知识的欲望和精神，希望大家能把对数学学习的态度和热情继续保持下去！你们能做到吗？

师：确定位置的学习，对今天的社会进步又有哪些作用呢？（多领域的应用：经纬线的介绍与马航失联事件的说明，见图4）希望学生能把知识学以致用，学会用数学的眼光观察生活。

图4

评析：通过笛卡儿故事的介绍，让学生得到数学文化的熏陶，进而激发他们学习数学的兴趣与增强学习的信心。另外，数学知识的学习不仅局限于书本，应该将学习的知识与实际生活相联系，学以致用，哪怕是让学生知道和体会其学习的用途。

三、学习体验

1.创设简明数学情境，增强“数对”学习体验

本节课紧紧围绕学生的座位情境进行教学，从一开始找小军座位，描述自己在班级中的位置——抽象到点的位置——用数对说位置——考考学生反应能力等过程，学生一直沉浸在列数与行数确定置的方法体验与抽象思维的形成上，最终掌握用数对确定位置这样一种简单有效的方法。在情境中，结合找座位，说座位，快速站立，不断巩固确定位置的相关知识与方法，让学生在“动手”与“动脑”相结合的学习活动中，获得较为深刻的学习体验。[1]正如学生所言：“今天我们学习用数对表示自己的位置，可以让一行或一列同学站起来，更神奇的是还可以让全班都站起来，给我的印象太深了”。

2.设计简洁“数对符号”，交流学习体验

数对的引入，老师没有直接告诉，而是提出制造一种符号使用的需要：“怎样才能快速地记录这些位置呢？”在认知冲突中，让学生感受“符号化”的作用，从而更加感受数学符号的简洁和魅力。在展示学生设计的表示位置的方法（4列3行，4-3,4L3h等）中，让学生相互交流、探讨方法的合理性，最终使学生发现统一的数对符号表示、设计简洁数对符号表示的需要。学生在交流的学习体验中，加深了用数对确定位置的学习体验。

正如学生所说：“这节课十分有趣，我知道了数对可以简便地写出准确的位置。”“听写的时候，我以为老师说的很慢，结果说的很快，当老师说完我才写好6个字。自己在设计的时候想如果用p4p3会认为是做第几页，最后我想先写一个小括号再写4和3，中间打一个点，可能会被认为是一个小数。最后老师教了我们一种，我觉得这种既简单，又好记。”

3.“数形结合”思想体验，促进学生思维发展

从“初次数学化”到“二次数学化”，让学生感受逐步进行数学抽象的过程；紧紧围绕确定位置的方法——“找列数与行数”，从“座位图”到“点子图”再到“方格图”，最后到解决“方格外的点”的位置。这样把一个个难题抛给学生，有的学生可能会在教师的引导下想到负数的概念，进而解决平面上点的位置的表示方法。[2]这是一种大胆的教学想法与尝试，从教学过程中学生的表现以及学生课后的学习心得发现，学生能通过这样的设计获得“数形结合”的思想体验。正如学生所言：“在确定位置这堂课中，我学到了许多，怎样确定位置以及数对的读法、用法等。老师还给我们说了数对的来历，以及那位科学家发现研究数对的过程。是啊！生活就是需要发现与观察，这样才能不断的创新、发展。”可见“授之以鱼不如授之以渔”。

[1]吕传汉，汪秉彝.论中小学“数学情境与提出问题”的教学[J].数学教育学报，2006，15（02）：74-79.

[2]弗赖登塔尔.作为教育任务的数学[M].陈昌平，唐瑞芬译，上海:上海教育出版社，1995.

责任编辑：熊显萍

Learning Experience Case on Applying Coordinate to Determine Position

JIANG Ling-ling1YU Jun2
（1.Experimental Primary School of Guiyang，Guiyang，Guizhou 550001,China; 2.The Teacher Study College of Nanming Township,Guiyang，Guizhou 550000,China）

From process of using the column and line to determine the location in real life，the students inquiry the ways on applying coordinate to determine position the location of points.The students development and application of mathematical reasoning in Mathematic thing.

Mathematic thing;Number and shape;Learning experience

1009—0673（2016）03—0109—05

G623.5

A

2016—04—15

蒋玲玲（1987— ），女，贵州贵阳人，贵阳市第一实验小学数学高级教师，主要从事小学数学教学工作。