强化数学意识 提升数学素养

■高桂霞

强化数学意识 提升数学素养

■高桂霞

天津市宝坻区霍各庄镇北马中心小学数学教师

●用微薄的力量，培养智慧之花，创造美好未来。

●知识能帮助人们开启智慧，改变生活，实现梦想。

●把工作中的困难当作一级级台阶，只要善于攀登，一定能达到光辉的顶点。

●把教学中的问题看作一盏点亮的灯，想到它所辐射的空间，以此来培养学生的开放性思维。

在我们这所极不起眼的农村小学，高老师十几年如一日执著地诠释着爱心和奉献。她温和娴静，少言寡语，却藏不住对孩子们的那颗火热的心。在她眼里，每个孩子都是明天的太阳，她把满腔的爱遍洒所有孩子。她希望孩子们都能健康茁壮成长，用知识改变命运，改变家乡的面貌。

高老师严谨谦恭，一丝不苟，所以练就了扎实的教学技能。在大家眼里，她是个闲不住的人，教学常规工作之余，她虚心求教，默默探索。兼任数学和科学两个学科，她却都不放弃，数年没日没夜地探索实践，始终站在我区课堂教学改革的前沿。

高老师背后付出的辛苦，让她赢得了一个又一个光环，我们却始终看不到她沾沾自喜、懈怠不前。家乡的教育事业似海无际无边，她恰是不知疲倦的船，她心中的希望和信念便是催她乘风破浪的帆。

——祝帆顺风，愿船平安！（天津市宝坻区霍各庄镇北马中心小学校长唐荣发）

数学意识指学生在面对问题时，依据条件和问题选择合适的解题策略，寻找解决问题的突破口的能力。强化数学意识可以使学生从被动接受到主动探索，从被动积累到主动感悟，把解决问题当作一个开启心智的过程，使解题有的放矢，如行云流水一般自然流畅，体现了思维体操的韵律美，最终成为减负增效的有效途径。

一、预见意识

对教师来讲，预见需要综合各方面的因素，预见可能出现的情况，及时调整方向，把握探究的节奏，更好地驾驭课堂。对学生来讲，养成预见意识可以发现一些隐含条件，确定解题策略，或借助特例迅速得到答案。准确科学的预测，能为解题提供优化的解题方案。

如用简便的方法计算6666×1667，从数字的特点来看，每个因数都不是5、25和125的倍数，可以预测到不能应用凑整先算的方法进行简算。两个数相乘，在没有特殊因数的情况下要进行简算至少有一个因数接近整十、整百、整千、整万……正用乘法分配律。基于这个策略，利用积不变的性质，把6666缩小到它的六分之一，把1667扩大到它的六倍再进行简算。

预见意识的形成要以数学思想、数学模型、解题策略为依托，是日积月累的结果，只有长期不懈的努力，才会从量变到质变，逐步提高预见的科学性和准确性。

二、化归意识

化归意识即转化意识，所谓转化就是把要解决的问题转化成已经解决的问题。无论是教学中把小数乘除法转化成整数乘除法，把求平行四边形的面积转化为求长方形的面积，把求三角形、梯形的面积转化为求平行四边形的面积，还是在解决问题时，数与形的互化、动与静的互化、特殊与一般的互化，无不渗透着转化的思想，可以说数学无处不化归。

在小学数学阶段，转化包括转化条件、转化问题和转化数量关系。如，妈妈去商店买布，所带的钱刚好可买甲种布6米或乙种布9米或丙种布18米，她想三种布买同样多，问最多能买几米？

把此题转化为：一项工程甲单独做6天完成，乙单独做9天完成，丙单独做18天完成，如果三队合作，问几天可以完成?

他山之石，可以攻玉。强化化归意识，恰当运用转化思想方法解决问题，不仅能提高解题效率，而且能使学生提高构建数学模型的能力，加深对知识的深度理解，抓住知识间的内在联系，构筑完整的知识体系。

三、整体意识

在数学活动中，善于从大处着眼，由整体（或全局）入手，将一些看似缺少条件无法解决的问题视为一个整体去思考与分析，常常可以起到化难为易的效果，摆脱常规模式的束缚。如，在求组合图形面积时，基本方法有割、补、平移、旋转、折叠、重叠等。但应用这些方法的前提是必须具备整体意识，只有具备了整体意识，才能根据题目的特点运用合适的方法解决问题。

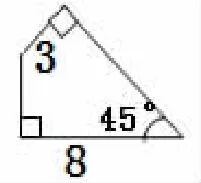
求这个图形的面积时，学生把它分割成两个直角三角形或补成一个梯形，由于缺少必要的条件不能解决这个问题。针对这种情况，我适时画了长颈鹿、松鼠的简笔画，当学生看到长颈鹿的脖子和松鼠的尾巴，就猜出了这两种动物。于是学生们受到了启发，预见这个图形是等腰直角三角形的一部分，问题迎刃而解。

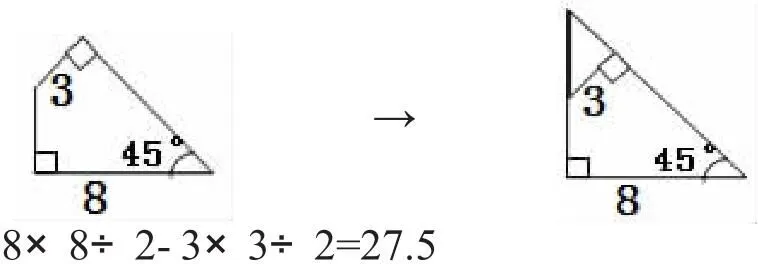
由此可见，整体意识就是站在最高点观察问题的全貌，不拘于小节。从结构特征入手，全面考虑问题，培养总工程师的理念。整体意识不但是学生永远追求的目标，也是我们教师追求的境界。

四、开放意识

开放意识主要培养学生的发散思维，学生通过多角度、多标准观察同一个问题，而得出不同的结论，培养学生全面、具体地解决问题。它不同于一题多解，不同的视角会得出不同的结果。

如一个等腰三角形，盖住两个角，露出一个大于40°而小于50°的角。这个三角形按角分是什么类型的三角形？

解决这个问题要分两种情况：

如果露出的这个锐角是等腰三角形的顶角，两个底角的和小于140°大于130°，每个底角小于70°大于65°，所以这个三角形一定是锐角三角形。

如果露出的这个锐角是等腰三角形的底角：

①这个锐角大于40°而小于45°时，那么三角形的顶角将大于90°，所以这个三角形一定是钝角三角形。

②当这个锐角等于45°时，那么三角形的顶角将等于90°，所以这个三角形一定是直角三角形。

③当这个锐角大于45°而小于50°时，那么三角形的顶角将小于90°，所以这个三角形一定是锐角三角形。

由此可见，强化开放意识，有利于培养学生良好的思维品质，能有效地激发学生敢于从多角度去观察、分析和解决问题，在采用不同的标准得出不同结论的过程中，培养学生的求异思维和发散思维。在主动参与知识建构的过程中，培养学生思维的广阔性、灵活性和独创性。

除上述四种常见的数学意识外，还有许多数学意识需要在数学学习中建立并强化出来。要达到运筹帷幄、决胜千里的境界，需要教师把强化数学意识，提升数学素养作为教学工作的核心任务。

我推荐的书

☉《寻找教育的支点》，茅晓辉、陈可伟著，光明日报出版社

☉《心与教育的对话》，武宏伟著，北京师范大学出版社

☉《教育科研与教师成长》，陈大伟著，华东师范大学出版社