基于云计算的最大频繁项集挖掘算法

孙鹤旭，孙泽贤，林　涛

(河北工业大学 控制科学与工程学院，天津 300130)



基于云计算的最大频繁项集挖掘算法

孙鹤旭，孙泽贤*，林涛

(河北工业大学 控制科学与工程学院，天津 300130)

针对目前海量数据挖掘过程中存在着频繁项集挖掘效率低、冗余项集繁多的问题，提出了改进的频繁模式树和遗传算法(FPGA),该算法鉴于异构数据的差异性特征，采用改进的频繁模式树和基于MapReduce的并行遗传算法搜索最大频繁项集，缩小了搜索范围，提高了挖掘效率.实验结果表明：该算法在时间复杂度方面有了很大提高，与传统的FP_Growth算法相比，具有更好的加速比以及更高的执行效率.

遗传算法；云计算；FP_Growth算法；最大频繁项集

近年来，不同结构类型的数据呈现几何、爆炸式的增长，海量异构数据在日常的应用中扮演着关键角色，传统的数据管理系统已经很难适应目前的发展形势.挖掘异构数据的研究主要分为分类挖掘、关联规则挖掘、聚类挖掘等，其中关联规则挖掘是重要问题之一.关联规则挖掘和频繁项集挖掘有着紧密的联系，频繁项集挖掘是关联规则挖掘的先决条件.由于在频繁项集挖掘的过程中，往往存在着结果项集数量十分庞大，挖掘效率较差的问题，影响了挖掘结果的应用与理解.为了解决上述问题，文献[1]通过构造支持度函数、关键字筛选技术，减小了内存消耗，去除了用户不关心的冗余信息，但仍然采用的是传统的串行计算方法.文献[2]、[5-7]、[9]利用了MapReduce的并行计算优势，但并没有对挖掘算法进行改进，只是单纯的提高了挖掘效率，依然存在挖掘结果数量庞大、冗余信息多的缺点.文献[3]提出了UFPGA算法，利用缩小变异空间的遗传算法搜索频繁项集，但没有考虑到算法的性能问题.文献[4]结合模糊集理论和Apriori算法，提出了模糊加权关联规则挖掘算法，提高了算法的挖掘效率，但却依然存在冗余的规则.文献[8]基于DCI-Closed-Index闭项集挖掘算法引入了全新的剪枝策略，设计了一个元项集的挖掘策略，挖掘效果得到了很大提高.

针对以上问题，本文提出了基于遗传算法和FP_Growth挖掘算法的组合思想，有效地减少了检测数据的数量，降低了搜索空间.而且，有效地减少了挖掘过程中的迭代次数，得到更加准确的条件模式基；另外，结合MapReduce并行计算模式，对遗传算法、FP_Growth算法的各个步骤并行化，不仅提高了挖掘效率，消除了冗余结果，而且可减少内存消耗，解决了内存不足的问题.

1　最大频繁项集挖掘方法

1.1构建原频繁模式树

在构建原频繁模式树时，针对FP-Growth算法扫描原始事务数据库时，受制于单机计算能力、网络带宽能力的缺陷，在挖掘大数据集的过程中需要大量的I/O开销；因此，本文结合MapReduce框架进行并行计算，提高计算效率，并将原始事务数据库转换为布尔矩阵，减少对事务数据库的扫描次数.即FPMP算法(FP-Growth结合MapReduce)，给定一个原始事务数据库TD(如表1所示)以及最小支持度min_sup,FPMP算法利用两次MapReduce来构建原频繁模式树，FPMP算法具体流程如图1所示.

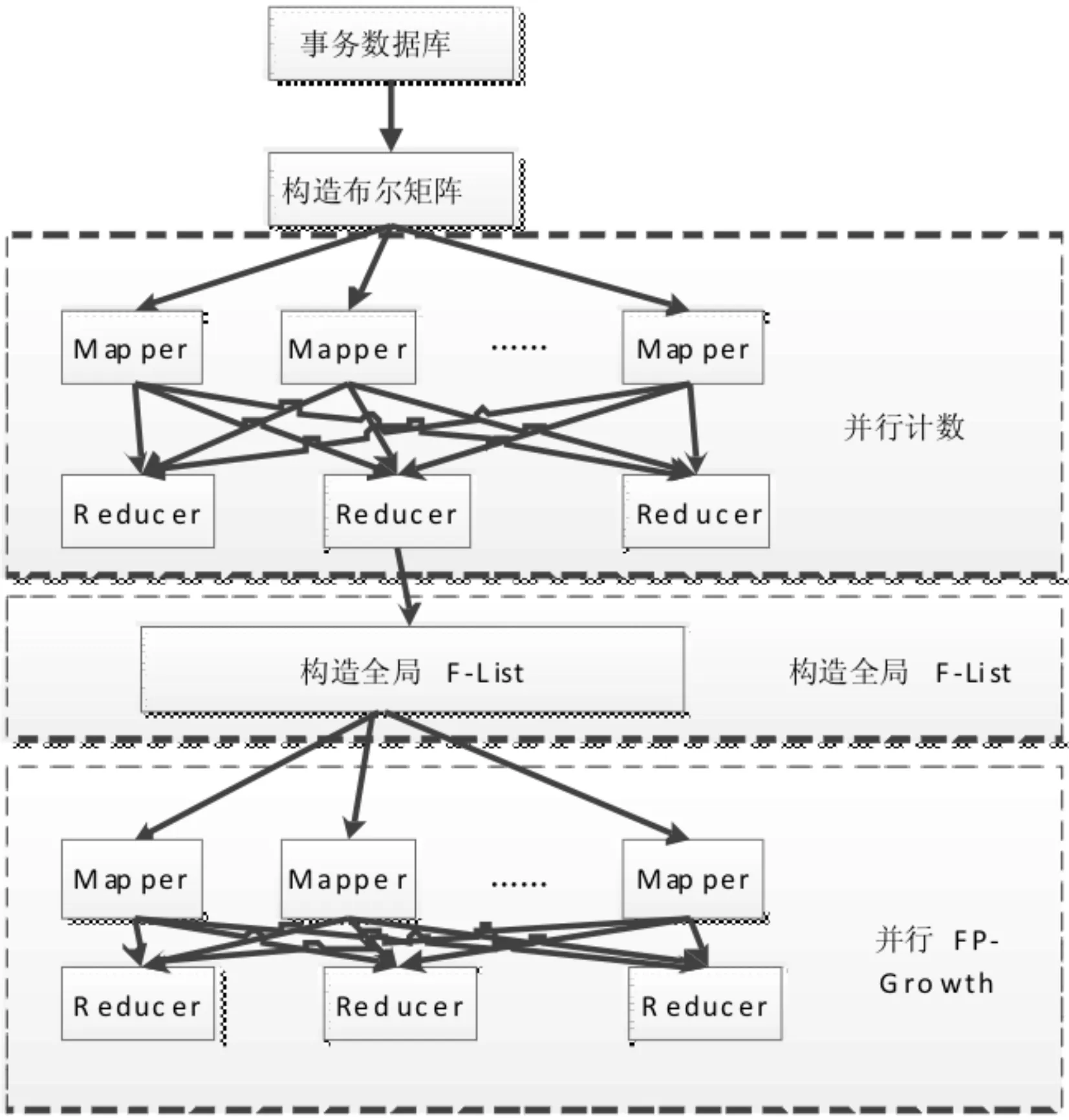
图1　构建原频繁模式树算法流程图Fig.1　Flow chart of the FPMP

其算法步骤如下.

(1) 构建布尔矩阵：将原始事务数据库TD(m个事务，n个项)转换为布尔矩阵A=(aij)m×n，aij代表TD中的项，若项存在，则aij=1，否则为0.

(2) 分片：根据MapReduce中从节点的个数，将矩阵A垂直划分为s个子矩阵(A1,A2，As),前s-1个分块的数据大小相等，即子矩阵的列数均为

ceil(n/s)，最后一个子矩阵的列数为n-(s-1)×ceil(n/s).

(3) 并行计数：并行扫描原始事务数据库，记录每一项的支持度.

(4) 构造全局F-List：传统算法在构建全局F-List的过程中，需要从第一项开始遍历，查找对应的项名称以及支持度，即只能进行顺序查找，随着项集数量的增加，遍历时间也会增加，严重影响算法执行效率.

本文通过设定一个地址函数f(In)，实现项名称In与存储地址f(In)的映射，并将支持度存入该地址中.在查找某项的支持度时，通过地址函数计算得出项地址，进而直接获得支持度，而无需从第一项开始遍历，时间复杂度由n提高到1.

例如，对表1的事务数据库，其传统的存储结构如表2所示，本算法的存储结构如表3所示.

表1　事务数据库

表2　传统算法存储结构

表3　改进的存储结构

对比频繁项列表F-List的存储结构表2、3可知，本算法效率的提高主要体现在：第2次扫描原始事务数据库时，删除非频繁项，并按照F-List的顺序降序排列.如果存在多个项的支持度计数相等时，改进算法只需比较地址函数的值，便可以判定项的顺序.

(5) 并行FP-Growth：在Map阶段，依据第(4)步得到的F-List，构造每个项的条件模式基.在Reduce阶段，根据条件模式基构建原频繁模式树.

1.2构建有序频繁模式树

定义1在事务数据库TD中，挖掘的结果项集X是频繁项集，如果不存在频繁项集Y，满足X⊂Y，|Y|=|X|+1，则X为最大频繁项集.

有序频繁模式树(OFPT)将TD中的项压缩到原频繁模式树(FPT)中，利用支持度计算频繁模式树上的高支持度集，使得树节点代表计算的项集，以此构建树结构.

在构建OFPT时，首先构建FPT.对于表1的事务数据库，设定其最小支持度阈值为3，1-项集集合为{(B：14)，(C：13)，(A：12)，(D：10)，(E：3)}，构建的FPT如图2所示.

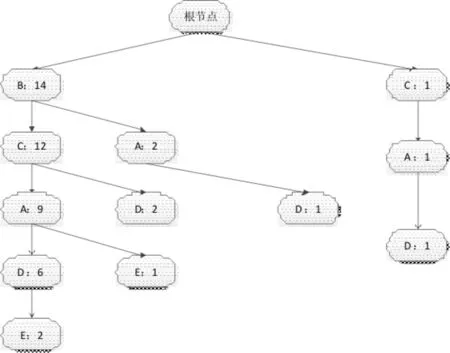
图2　原频繁模式树Fig.2　Original frequent pattern tree

之后，复制FPT作为OFPT的树干，遍历FPT的第一层的项{(B：14)、(C：1)}，统计下层的分支链为{(C：12-A：9-D：6-E:2)，(A：2-D：1)，(C：0-D：2)，(C：0-A：0-E：1)，(A：1-D：1)}，将分支链看做对应的事务压缩到OFPT中，同时，节点的支持度计数也要累加到投影点上.然后在下一层的项{(C：12)、(A：2)、(C：1)}继续投影，直到最后一层{(E：2)}投影完成，最终OFPT如图3所示.

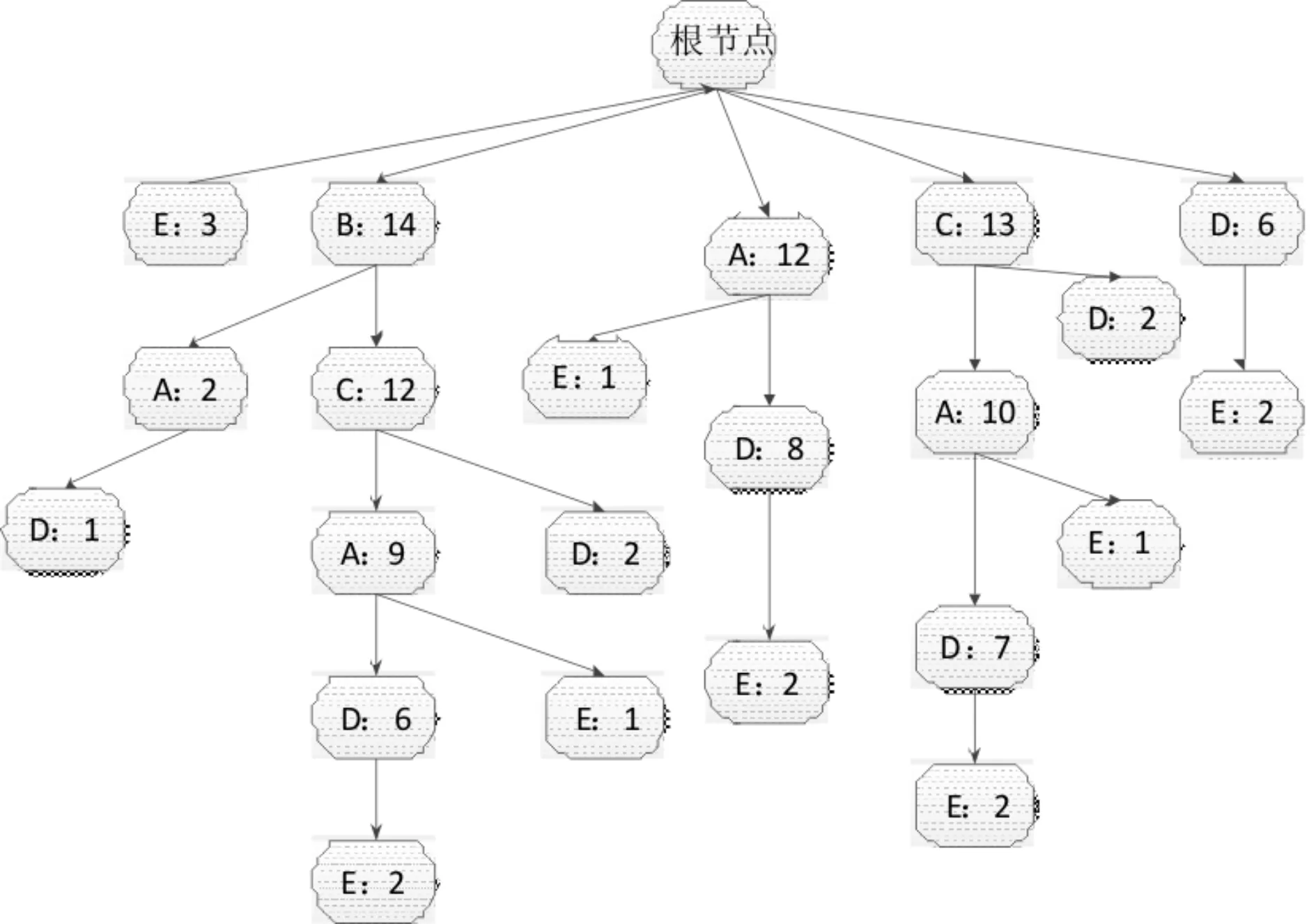
图3　最终的有序频繁模式树Fig.3　Ordered frequent pattern tree

根据定义1可知，在OFPT中如果存在一个节点r对应的项集为频繁项集，而下一层节点r+1对应的项集不是频繁项集，那么节点r即为所在分支链的最大频繁项集.依据此规律，采用基于MapReduce的并行遗传算法，利用其全局搜索性、随机性、并行性计算的特点，搜索各分支链的最大频繁项集.

1.3基于并行遗传算法的最大频繁项集挖掘

对于传统的遗传算法，在搜索最大频繁项集的过程中，具有搜索不完全、迭代次数过多的缺陷.因此，本算法结合MapReduce并行计算模型，改进了变异运算，提高了搜索准确性.算法具体描述如下.

(1) 编码：算法采用十进制编码规则.首先，统计OFPT中分支链的数量作为染色体的长度，每条分支链对应一个基因位，每条分支链上的节点代表该基因位有几种基因值，基因z取值范围为[1,zmax]，zmax为OFPT中根节点到叶子节点的节点数(不包括根节点).

(2) 初始化种群：将整个种群分为n个子种群，每一个子种群由一个MapReduce任务负责.

(3) 适应度函数：为了保证基因值对应的是最大频繁项集，采用如下的对应函数：

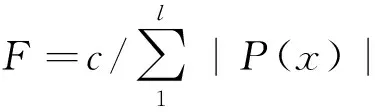
(1)

其中，c为比例参数，取值为10的倍数，取决于初始化种群大小，这样能够保证复制到下一代的个体为优秀个体.l为OFPT分支链数量，即染色体长度.在Map阶段计算子种群中个体的适应度值，在根据子种群数量以及Reduce数量，将各子群分配到Reduce任务中，首先暂存各子群，之后再在Reduce阶段执行选择、交叉、变异操作.

(4) 选择和交叉：本算法采用轮盘赌法，基于适用度比例选择优秀个体；交叉操作采用均匀交叉对种群个体进行随机配对.

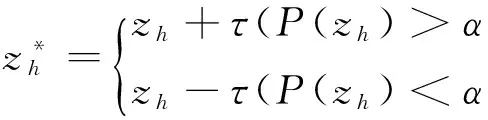
(2)

并行遗传算法流程图如图4所示，由上述过程可知，这里仅需计算少量频繁项集.然后按照定义1搜索最大频繁项集，并且将MapReduce并行计算模式和遗传算法一起应用到FP_Growth算法上，提高了算法的整体性能.

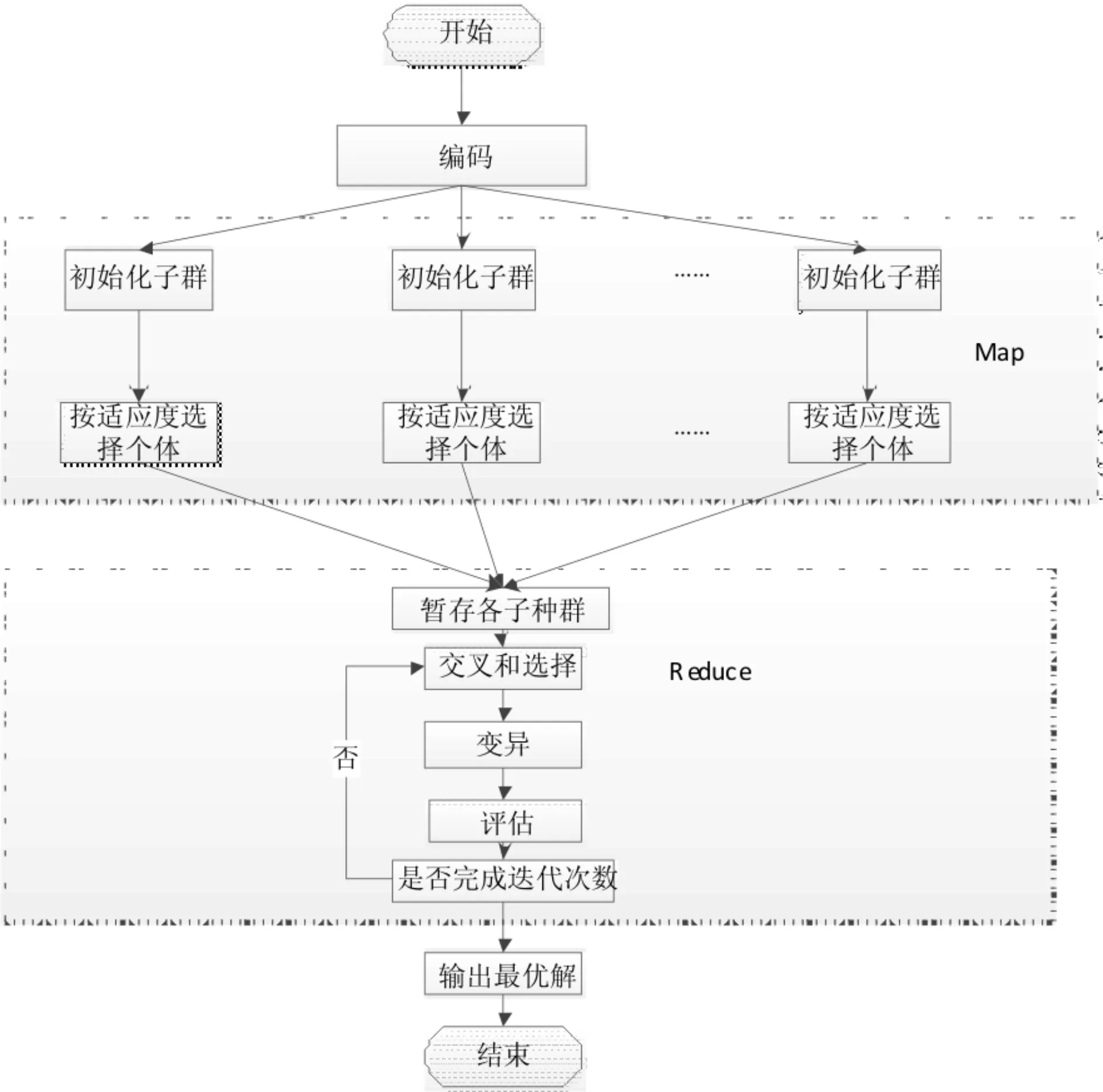
图4　并行遗传算法流程图Fig.4　Flowchart of the Parallel genetic algorithm

1.4FPGA算法流程

FPGA算法描述如下.

输入：原始事务数据库TD，最小支持度，概率阈值.

输出：最大频繁项集.

a. 构建FPT：利用MapReduce的并行计算模式，结合地址函数有效地提高了算法的时间复杂度.

b. 构建OFPT：将FPT中每一层节点投影到OFPT中，直到最后一层结束.

c. 修减OFPT：将每条支链中支持度小于ω的节点去掉.

d. 编码：遍历OFPT，统计分支链条数L和最大节点个数，将染色体的每一个基因位赋值，并进行十进制编码.

e. 随机初始化子种群：每一个子种群由一个MapReduce任务负责，在Map阶段进行适应度选择，并将各子群分配到对应的Reduce任务中.

f. 按照公式(1)计算各适应度，并以此进行选择、交叉、变异操作.

g. 重复f操作，直到流程结束，输出挖掘的频繁项集.

综上所述，FPGA算法采用地址函数、MapReduce并行计算模型、遗传算法优化了FP_Growth算法，具有更好的加速比、更好的执行效率，节省了内存资源.

2　实验结果及分析

本文实验平台的基本配置如表4所示，1个NameNode，3个DataNode，操作系统为CentOS release 5.6，Mapper和Reducer的最大负载都配置为2，其他配置都采用Hadoop的默认配置.

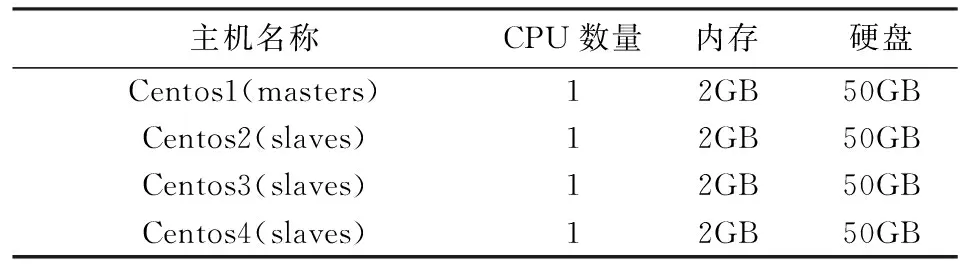
表4　实验平台基本配置

设定最小支持度为10%、20%、30%、40%、50%，采用某公司货物供应商数据集进行试验，总计有12790431条事务，事务数据库涉及3210个项.文献[9]在分析了传统的FP_Growth算法的基础上，针对单路径和多路径的不同挖掘算法，提出了Pruned FP-tree算法，结合MapReduce计算模式，实现了算法流程的并行化，提高了对海量数据的处理能力；然而，它并没有对FP_Growth算法进行改进，算法依旧需要对数据库进行重复扫描.因此，在构建原频繁模式树时，FPGA算法借鉴文献[9]的思想，利用MapReduce的并行计算的优势，结合地址函数的思想，有效地减小了时间开销，FPGA算法与Pruned FP-tree算法的性能比较如图5所示.

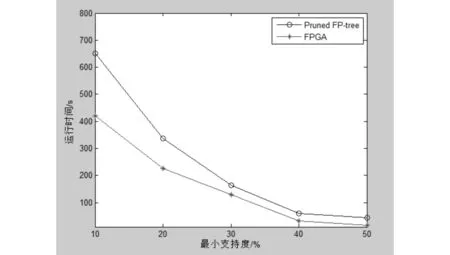
图5　FPGA与FP_Growth性能比较Fig.5　The comparison between the FPGA and FP_Growth

定义2加速比即为在Hadoop框架下单节点算法执行时间t1和多节点算法执行时间tp之比.如公式(3)所示：

Sp=t1/tp.

(3)

本文通过加速比来评估FPGA算法在挖掘最大频繁项集中的整体性能.在同义事务数据库的前提下，通过对比不同最小支持度、不同工作节点数的加速比，证明了FPGA算法的优越性.

如图6 所示，不同最小支持度的加速比是不一致的，加速比在最初阶段会随着节点数的增加而变大，但由于节点数量增加会造成通信负载的增大，使得加速比的增长趋于稳定.由图6可知，在最小支持度变大时，频繁项集的数量会减少，并行遗传算法搜索的项集也就会减少，因此加速比的增长也就开始降低.

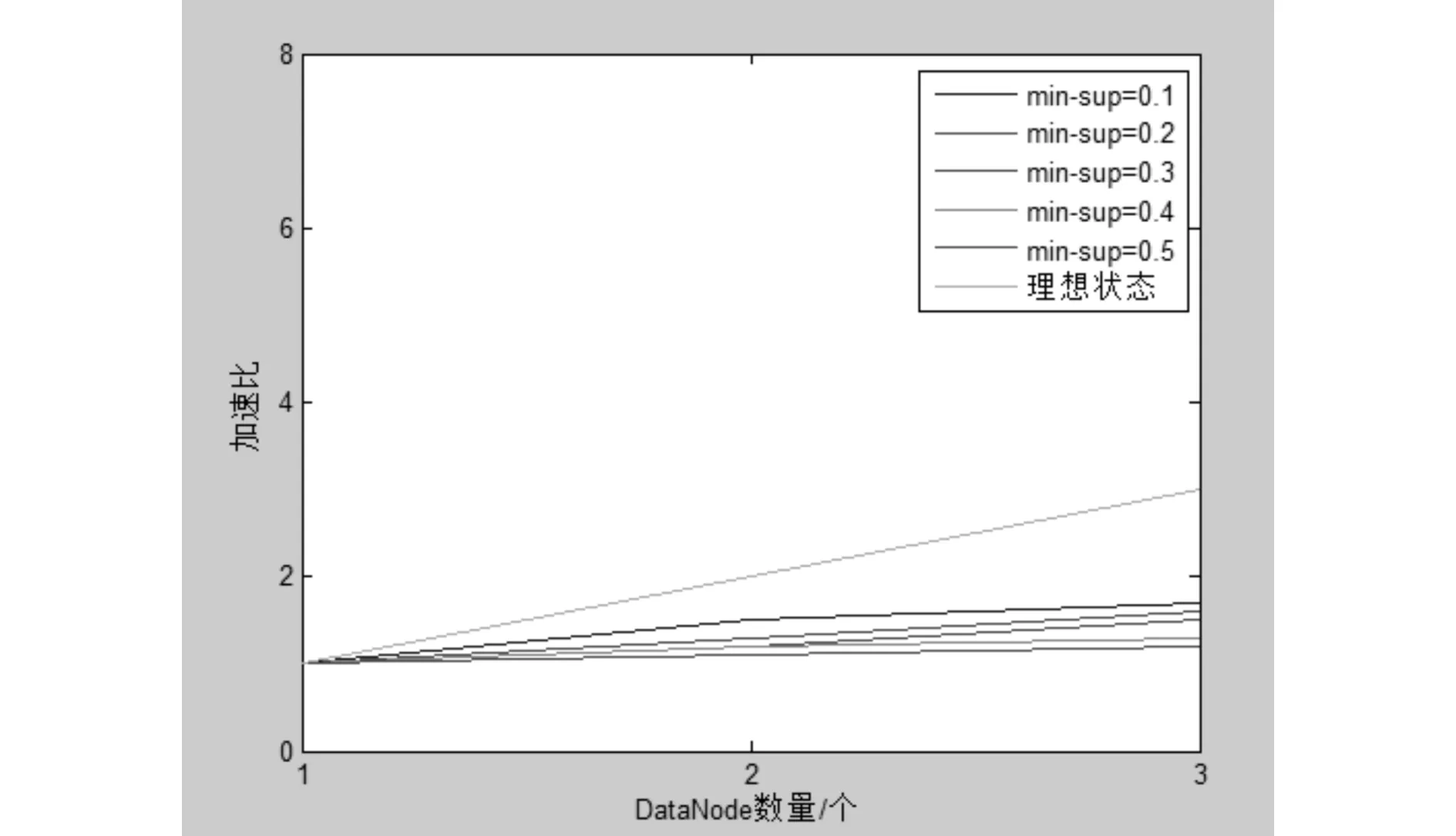
图6　FPGA算法的加速比Fig.6 The speed-up raios of the FPGA

3　结束语

本文提出一种基于Hadoop的，将FP_Growth算法和遗传算法相结合的最大频繁项集挖掘算法.该算法主要由6步组成：构建原频繁模式树，构建有序频繁模式树，修减有序频繁模式树，编码，随机初始化子种群，选择、交叉、变异，最终挖掘出最大频繁项集.实验表明该算法是十分有效的，本文的主要创新

点是：将FP_Growth算法并行化，结合地址函数，快速构建原频繁模式树；在挖掘最大频繁项集的过程中，利用遗传函数的全局搜索性、随机性，再结合MapReduce的并行计算模型，提高了整体挖掘效率.但本文也有一定的不足之处，如果数据集较小，采用MapReduce则会降低算法执行效率，则没有并行化的必要，这是以后仍需改进的地方.

[1]李宏光,夏丽君. 改进的FP-growth算法及其在TE过程故障诊断中的应用[J]. 北京工业大学学报,2016(05):697-706.

[2]周国军,龚榆桐. 基于MapReduce和矩阵的频繁项集挖掘算法[J]. 微电子学与计算机,2016(5):119-123.

[3]唐向红,杨全纬,郑 阳. 挖掘不确定数据的最大频繁项集[J]. 华中科技大学学报(自然科学版),2015(9):29-34.

[4]王佳,李宏光. 工业报警序列的模糊关联规则挖掘方法[J]. 化工学报,2015(12):4922-4928.

[5]陈兴蜀,张帅,童浩,等. 基于布尔矩阵和MapReduce的FP-Growth算法[J]. 华南理工大学学报(自然科学版),2014(1):135-141.

[6]何波. 基于频繁模式树的分布式关联规则挖掘算法[J]. 控制与决策,2012(4):618-622.

[7]陈光鹏,杨育彬,高阳,等. 一种基于MapReduce的频繁闭项集挖掘算法[J]. 模式识别与人工智能,2012,25(2):220-224.

[8]宋威,李晋宏,徐章艳,等. 一种新的频繁项集精简表示方法及其挖掘算法的研究[J]. 计算机研究与发展,2010,47(2):277-285.

[9]杨勇,王伟. 一种基于MapReduce的并行FP-growth算法[J]. 重庆邮电大学学报(自然科学版),2013,25(5):651-657+670.

Mining Maximal Frequent Itemsets Based on Cloud Computing

SunHexu,SunZexian,LinTao

(Institute of Control Science and Engineering , Hebei University of Technology , Tianjin 300130, China)

Since efficiency and accuracy of mining frequent itemsets is not very high in mass data,an improved FPGA algorithm was proposed for mining them.According to the feactures of the mass data,the improved FP_Growth mines frequent itemsets and the parallel genetic algorithm was employed to search for the largest frequent patterns.FPGA althorithm sharnk the scope to improve the efficiency of the mining results.Experiments show that the FPGA althorithm is superior to the original one due to the high efficiency and speedup.

genetic althorithm;cloud computing;FP_Growth althorithm;maximal frequent itemsets

2016-06-30*通讯作者孙泽贤，研究方向：数据挖掘、云计算， E-mail：1249226957@qq.com

孙鹤旭(1956-)，男，教授，博士生导师，研究方向：自动化,E-mail：shx13682168380@sina.com

天津市科技支撑资助项目(14ZCDZGX00818)

TP3

A

1672-4321(2016)03-0102-05