基于MPSP的次优滑模制导律
李帅, 李新国
(1.西北工业大学 航天学院, 陕西 西安 710072;2.西北工业大学 航天飞行动力学技术国家重点实验室, 陕西 西安710072)
基于MPSP的次优滑模制导律
李帅1,2, 李新国1,2
(1.西北工业大学 航天学院, 陕西 西安 710072;2.西北工业大学 航天飞行动力学技术国家重点实验室, 陕西 西安710072)
针对导弹拦截机动目标的问题,提出了一种能满足多终端约束的次优滑模制导律(Sub-OSMG)。该算法将模型预测静态规划(MPSP)与滑模控制(SMC)相结合,解决了MPSP在系统模型不精确时由于依赖模型预测而导致的控制量发散问题;基于三自由度相对运动方程建立所提出的制导律,其鲁棒性通过Lyapunov稳定性理论进行了证明;在滑模控制的设计中引入一种较为新颖的滑模面,巧妙地继承了两种方法的优点,其区别于传统扩展比例导引(APN),在仅知机动幅值的情况下,能精确地击中目标。仿真结果表明,所提出的Sub-OSMG能够有效地抵消外部扰动,具有更高的精度、更好的鲁棒性、更小的控制代价。
制导; 最优控制; 多终端约束; 滑模控制; 模型预测静态规划; 鲁棒性
0 引言
到目前为止,由于在求解两点边值问题和高维系统上依赖梯度法或打靶法等,最优控制理论在制导方面的应用中需要大量的计算,一般仅应用于离线计算,作为指令存储在计算机中。而能够在线应用的最优制导律大部分都基于线性二次最优控制理论,获得反馈形式的控制量修正。然而,该方法一般需要参考轨迹,这在有些情况下并不可取。文献[1]提出了针对时变速度的一种闭环最优制导律,文献[2]将加速度指令与时间不确定项联系起来设计了最优制导律。而基于状态黎卡提方程(SDRE)的制导算法[3],需要在线反复求解黎卡提方程,系统维数较高时求解就变得很费力,甚至不可解。一个较为高效的方法即动态规划,类似SDRE需要求解HJB方程[4],然而HJB方程是一个非线性的偏微分方程组,求解亦是一个难点。
针对上述求解费力、耗时等问题,文献[5]将模型预测控制(Model Perdictive Control,MPC)与近似动态规划(Approximate Dynamic Programming,ADP)技术相结合,提出了模型预测静态规划 (Model Predictive Static Programming,MPSP)算法,该算法兼顾了计算效率与求解的难易程度,将传统的动态规划转化为静态规划问题求解,成功地将最优控制理论引入制导体系。在求解两点边值问题时,通过递归求解协状态变量以更新控制量,滚动修正误差。这样大大提高了计算效率,降低了计算复杂度。
然而,该最优制导算法(MPSP)需要精确的模型信息完成预测环节,若系统存在未知扰动或建模不确定项,预测部分将不能提供准确的反馈值,导致误差会随着系统运行积累,相当多的情况下便会发散。针对这一问题,很多学者利用滑模控制(Sliding Mode Control,SMC)对外部扰动的不敏感性,将最优控制与SMC相结合,提出了制导律。如文献[6]基于此,根据视线角变化率推导出了最优鲁棒制导律;文献[7]针对机动目标提出了一种最优滑模制导律;之后文献[8]进一步提出了有速度及终端约束的制导律;文献[9]在前人研究的基础上,利用SDRE获得最优解,通过设计滑模面进而获得另一种形式的制导律。
但是,上述方法依然存在计算复杂度过高、在线求解困难等问题。本文将MPSP与SMC相结合,充分利用MPSP的效率优势和SMC的抗干扰特性,设计了一种新颖的制导律,其在结构上兼顾了最优性与鲁棒性,将其应用于拦截机动目标制导中,验证了算法的有效性。
1 相对运动数学模型
图1给出了追踪问题弹目相对运动几何关系。以导弹初始位置建立惯性坐标系(x,y,z),根据相对关系建立弹目视线坐标系(r,θ,φ)。其中,r为导弹与目标的相对距离;θ和φ分别为视线方向角和高低角。

图1 三维相对运动几何关系Fig.1 3-D relative motion geometry

(1)
对上式两端再求导并整理,可得到3个方向的动力学方程:
(2)

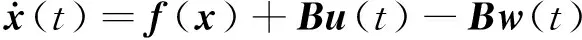
(3)
式中:f(x)为状态函数;B为控制矩阵;u,w 分别为导弹和目标的加速度,具体定义如下:
式中:视目标加速度w为系统扰动项。
2 控制量u的设计
2.1MPSP算法简述
考虑一非线性系统,离散化如下:
(4)

(5)
式中:dUk为控制量增量;Rk为加权矩阵。根据MPSP理论[5],控制增量为:
(6)

2.2带补偿项的MPSP算法
在MPSP算法基础上,设计补偿项结构。考虑一带扰动的仿射非线性系统:
(7)


(8)

(9)
假设初始控制量猜测值为up,du 为控制增量,末端约束为xd,性能指标为:
(10)
将其离散化,按照上一节MPSP算法可得控制量为:
(11)
为了补偿系统的不确定或外部扰动,将控制量设计为如下形式:
(12)
式中:后一项为补偿项,选择形式等价于SMC中等效控制ueq与udis。前者保证系统在滑动面上时满足约束并使能量最省;后者使系统对扰动保持不敏感。下文将基于SMC对ucomp进行设计。
3 次优滑模制导律
基于前文的设计,对式(3)设计如下的滑模面:
(13)
式中:G(x)∈Rm×n为系数矩阵,其保证G(x)B(x)非奇异。
由上式可知,在t=0时,s=0,即初始状态在滑模面上。对上式两边求导并结合式(3),可得:
(14)

(15)

(16)
式中:DL,DU为扰动上下界且已知。结合式(13)得补偿项为:
ucomp=-(GB)-1[ks+εsgn(s)]-Dc
(17)
其中:
根据Lyapunov稳定性理论,考虑如下李亚普诺夫函数:
(18)
(19)
(20)


(21)
式中:δ为很小的正常数。由此便可得到一种能满足多终端约束的次优滑模制导律:
(22)
4 仿真结果及分析
首先将本文的算法应用于一线性受扰系统,完成受扰动时的状态转移,其次将该方法应用于制导问题,视目标机动为系统扰动,假设按正弦曲线机动,在仅已知机动幅值情况下完成仿真,说明本文算法的有效性。
4.1考虑带扰动线性系统
系统方程如下:
(23)
式中:I3为三维单位矩阵;ν为控制量(标量);d为扰动项,假设d=Asinωt,其中A=5为幅值,ω=1 s-1为频率。初始状态x0=[1,1,1]T,终端约束xf=[0,-1,2]T,仿真时间t=10 s,初始控制量ν=0,仿真结果如图2、图3及表1所示。表1中,∞表示相对误差不存在(真值为0)。

图2 状态量曲线Fig.2 State variables

图3 控制量曲线Fig.3 Control variables

终端值x1x2x3MPSP末端-0.015-1.1151.278Sub-OSMG末端-0.003-1.0011.993期望值0-12MPSP相对误差/%∞11.536Sub-OSM相对误差/%∞0.10.35
可以看出,Sub-OSMG由于有补偿项,其状态量幅值较MPSP小很多,且MPSP在有未知扰动时未能满足终端约束。表1表明:其终端误差在受扰动时较后者大;控制量上,Sub-OSMG除初始时刻由于滑模的切换作用有抖振外,其值保持稳定,而MPSP控制量振幅逐渐在增大。
4.2考虑拦截机动目标问题

(24)
式中:χ为正常数;ξi=e-rkβ(i=1,2,3;β为正常数)。仿真结果如图4~图10所示。

图4 相对距离Fig.4 Relative distance
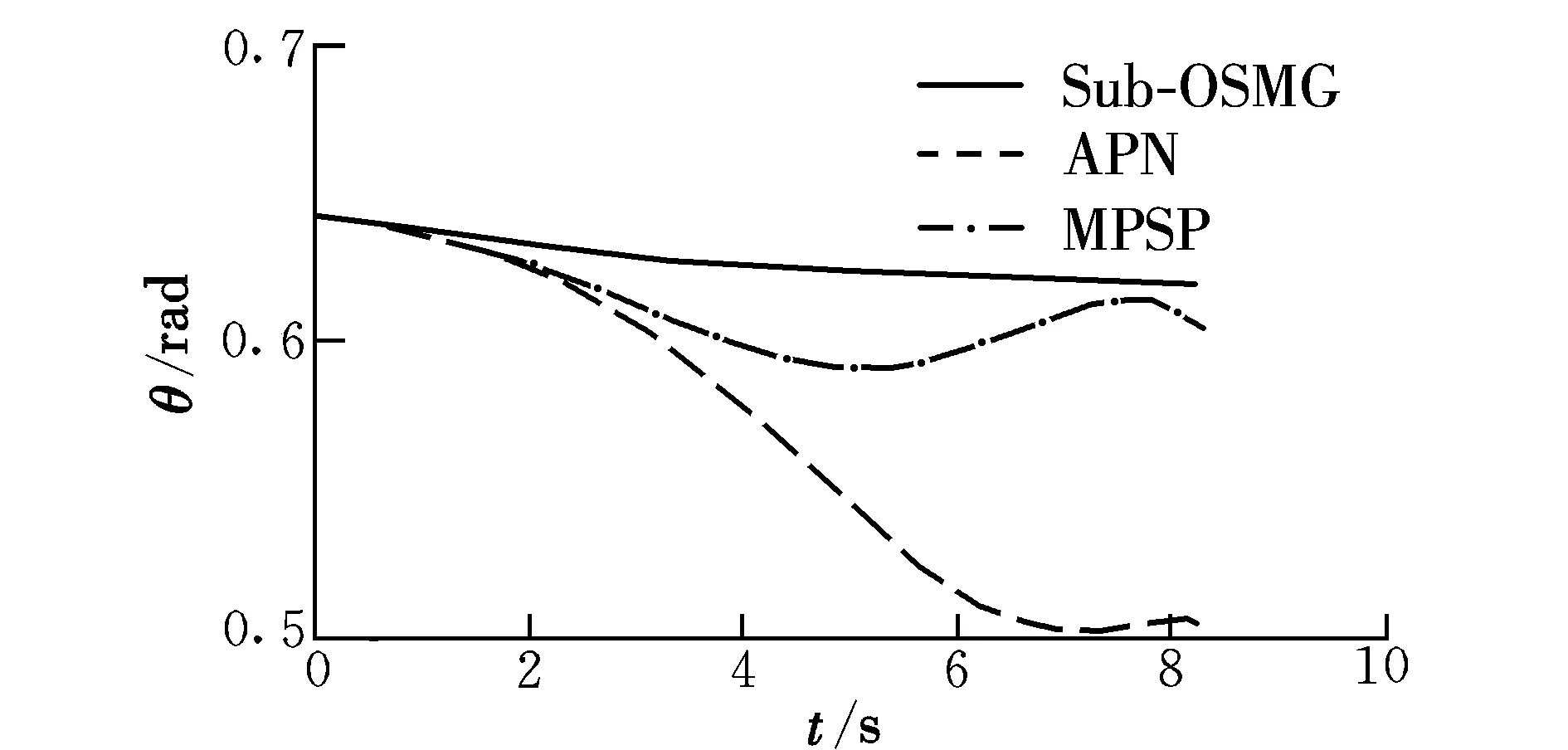
图5 方向角Fig.5 Azimuth angle

图6 高低角Fig.6 Angular altitude
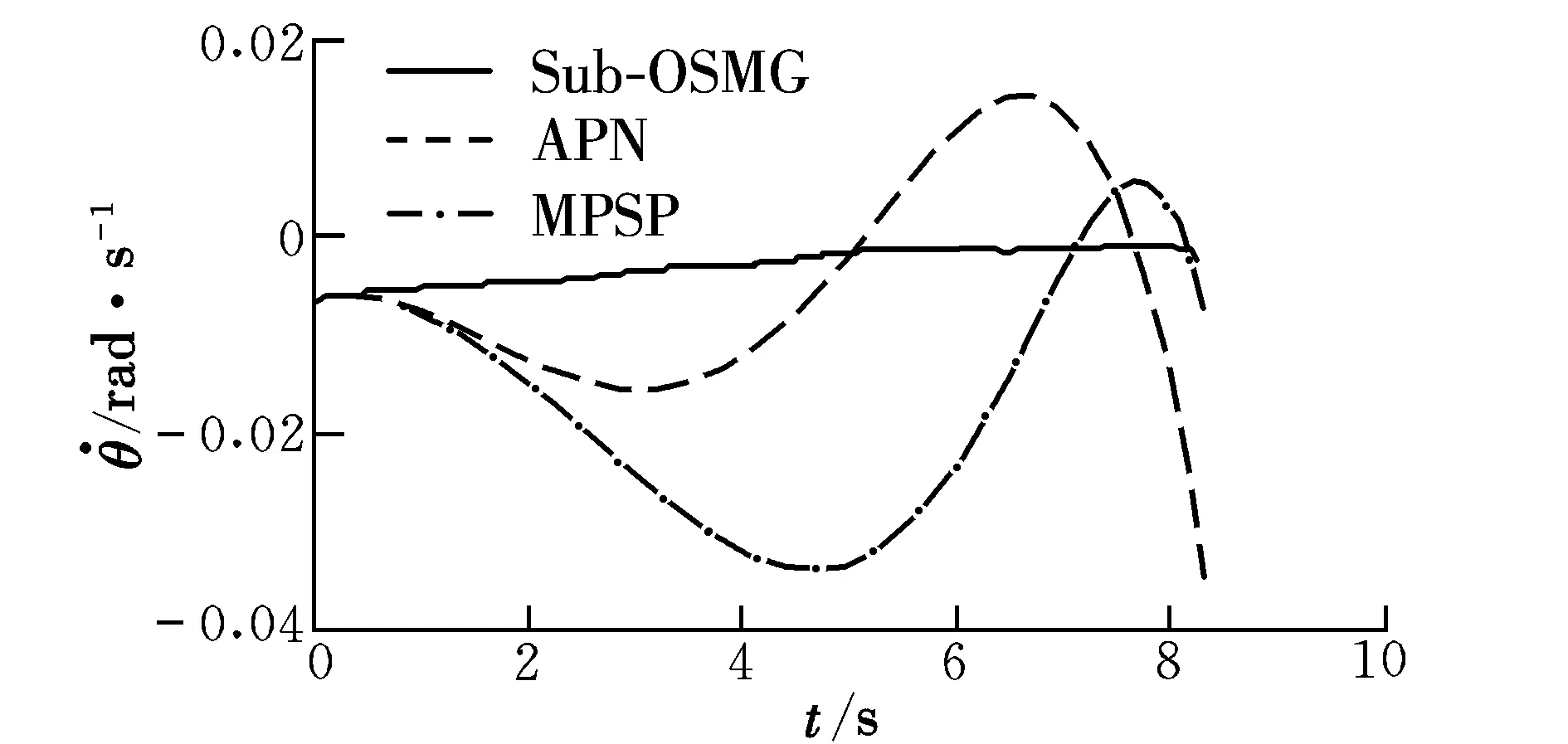
图7 方向角变化率Fig.7 Variation rate of azimuth angle

图8 高低角变化率Fig.8 Variation rate of angular altitude

图9 控制量uθFig.9 Control variable uθ

图10 控制量uφ Fig.10 Control variable uφ
从图4~图6中可以看出:三种算法并非均满足多终端距离及角度约束,APN本身无满足约束的能力;MPSP算法由于预测误差累计,最终未能击中目标;所提出的Sub-OSMG能够有效地抵抗外部干扰,实现了较高的精度。由图7和图8可知,除所提出的算法外,APN和MPSP角度变化率逐渐在增大,MPSP末端发散。由图9和图10可知,Sub-OSMG算法的控制量幅值最小,且较为平滑,在末端时均接近0。
5 结束语
本文在综合分析MPSP及SMC基本理论的基础上,将两者结合提出了一种较为新颖的次优制导算法。经仿真验证表明:该算法对系统不确定性或存在干扰时具有鲁棒性,且保持了MPSP的解析性及次优性的优点,能满足多终端约束,制导精度较高,并且具有一般性,对两点边值问题或状态转移问题同样适用。综合分析表明,所提出的制导律是一种较为有效的算法。
[1]Cho H,Ryoo C K,Tahk M J.Closed-form optimal guidance law for missiles of time-varying velocity[J].Journal of Guidance,Control,and Dynamics,1996,19(5):1017-1023.
[2]Yaesh I,Ben-Asher J Z.Optimal guidance with a single uncertain time lag[J].Journal of Guidance,Control,and Dynamics,1995,18(5):981-988.
[3]Mracek C P,Cloutier J R.Control designs for the nonlinear benchmark problem via state-dependent Riccati equation method[J].International Journal of Robust and Nonlinear Control,1998,8(4/5):401-433.
[4]Bryson J A E,Ho Y C.Applied optimal control: optimization,estimation and control[M].USA:N J,New York Press,1975:128-147,177-211.
[5]Padhi R,Kothari M.Model predictive static programming:a computationally efficient technique for suboptimal control design[J].International Journal of Innovative Computing,Information,and Control,2009,5(2):399-411.
[6]Zhou D,Mu C,Ling Q,et al.Optimal sliding-mode guidance of homing-missile[C]//Proceedings of the 38th IEEE Conference Decision and Control.Phoenix,AZ,1999:5131-5136.
[7]Bahrami M,Ebrahimi B,Roshanian J.Optimal sliding-mode guidance law for fixed-interval propulsive maneuvers[C]//Proceedings of IEEE Conference on Control Application.Munich,Germany,2006:1014-1018.
[8]Ebrahimi B,Bahrami M,Roshanian J.Optimal sliding mode guidance with terminal velocity constraint for fixed interval propulsive maneuvers[J].Acta Astronautica,2008,62(10):556-562.
[9]Seyyed Sajjad Moosapour,Ghasem Alizadeh,Sohrab Khanmohammadi,et al.A novel nonlinear robust guidance law design based on sdre technique[J].Journal of Aeronautical and Space Sciences,2012,13(3):369-376.
(编辑:姚妙慧)
Sub-optimal sliding mode guidance law based on MPSP
LI Shuai1,2, LI Xin-guo1,2
(1.School of Astronautics, NWPU, Xi’an 710072, China;2.National Key Laboratory of Aerospace Flight Dynamics, NWPU, Xi’an 710072, China)
A sub-optimal sliding mode guidance law(Sub-OSMG) which can satisfy the multiple terminal constraints is proposed for missile to intercept maneuvering target. By combining sliding-mode control(SMC) and model predictive static programming(MPSP), the results divergence problem of MPSP due to excessive dependence on model prediction when system model is inaccuracy can be solved successfully. The guidance law is established based on three degree of freedom motion equation and its robustness against disturbance is proved by Lyapunov theory. In sliding mode control a new sliding surface is introduced, so the proposed guidance law can inherit the merits of the two methods, it is therefore different from the conventional guidance law like APN and can accurately hit the target with only the maneuvering amplitude. Simulation results show that the Sub-OSMG is of higher accuracy, better robustness and lower control cost, and could effectively counteract the external disturbance.
guidance; optimal control; multiple terminal constraints; sliding-mode control; model predictive static programming; robustness
2015-11-19;
2016-03-30; 网络出版时间:2016-04-22 09:52
李帅(1989-),男,陕西西安人,博士研究生,研究方向为飞行器制导与控制。
TJ765.3
A
1002-0853(2016)05-0054-05

