区间二型不确定随机模糊系统的控制设计
陈玉平,周绍生
(1.杭州电子科技大学理学院,浙江 杭州 310018;2.杭州电子科技大学自动化学院,浙江 杭州 310018)
区间二型不确定随机模糊系统的控制设计
陈玉平1,周绍生2
(1.杭州电子科技大学理学院,浙江 杭州 310018;2.杭州电子科技大学自动化学院,浙江 杭州 310018)
研究了一类含有多Wiener过程的区间二型不确定It随机模糊系统的控制设计的问题.利用随机Lyapunov方法和不等式的放缩技巧,给出了闭环系统随机渐近稳定的充分条件;采用矩阵分解的方法,有效地处理了系统中的参数不确定性.最后通过仿真实验验证了闭环系统的随机稳定性.
区间二型模糊系统;随机系统;不确定
0 引 言
为了弥补一型模糊集合在描述不确定方面的缺陷,文献[1]在1975年提出了二型模糊集合理论.文献[2]提出了二型模糊集合的代数形式,解决了二型糊集合运算复杂的问题;并进一步提出了区间二型模糊集合的次隶属函数为1的概念,使运算的复杂性降低.区间二型模糊集能够处理一型模糊集合隶属函数存在的不确定性问题,采用三维的隶属函数表征多重不确定性来处理变量取值不精确、不确定的情形,相比一型模糊集合,能更好地表述系统的不确定信息,故近年来受到国内外学者的青睐,基于T-S模型的区间二型模糊系统的稳定性分析和控制器设计已有很多成果[3-4].此外,在过去的几十年中,随机系统已经引起了许多学者的广泛关注[5-6],也取得了不少成果.但是,目前在区间二型随机模糊系统方面的理论成果还不多,仍待继续研究.本文主要研究基于T-S模型的区间二型不确定随机模糊系统的镇定问题.带有多Wiener过程的随机扰动和参数不确定增加了研究系统镇定问题的难度.利用平行分布补偿方法设计反馈控制器,引入Kronecker积,采用不等式放缩方法及Schur补引理,建立了标称系统随机渐近稳定的充分条件.利用Kronecker积的性质以及矩阵分解的技巧[7],解决参数不确定性的问题,建立系统随机渐近稳定的充分条件.
1 系统描述
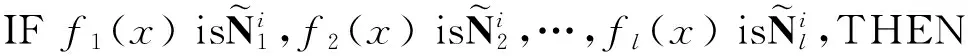

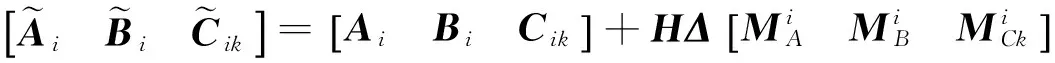
(2)
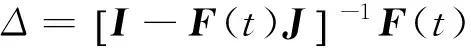
(3)
F(t)F(t)T≤I,
(4)
I-JJT>0.
(5)
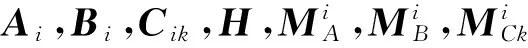

区间二型不确定随机模糊系统(1)可以表述为:

(6)

利用平行分布补偿法设计状态反馈控制器,其模糊规则描述如下:
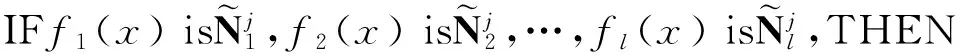
u=Kjx.
(7)


(8)
由式(6)和式(8)所确定的闭环模糊系统描述如下:

(9)

引理2[7]假设Δ满足式(2)-(5)并且矩阵M=MT,S和N具有适当维数,对于所有的式(4),不等式
M+SΔN+NTΔTST<0
(10)
成立,当且仅当对某一ε>0,都有
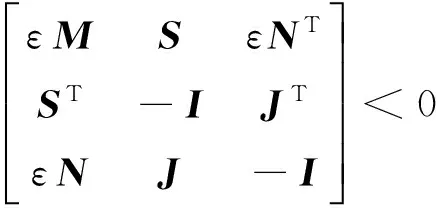
(11)
当Δ=0时,由闭环系统(9)可得到如下标称系统:

(12)
利用文献[8]中的类似方法,可得到如下引理:

(13)
需要说明的是,本文在引理3中,采取了与文献[8]稍不同的方法对LV(x)估计.
2 主要结果

(14)
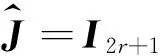
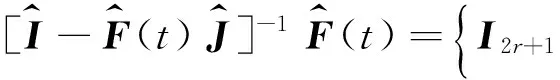
由式(14)可得:
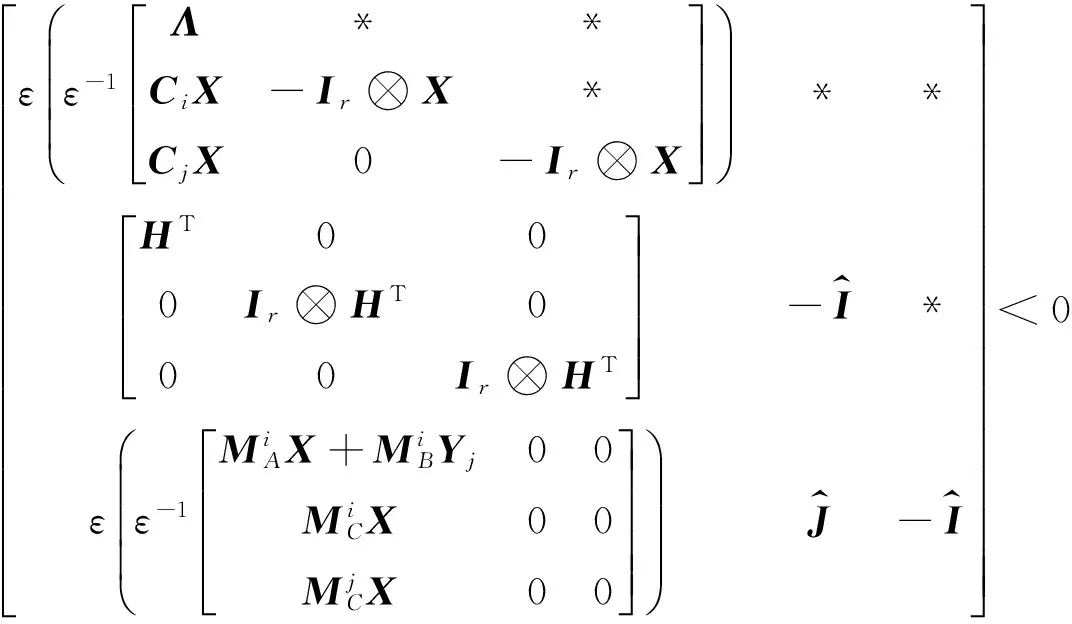
(15)
由式(15)及引理2可得:
(16)
通过计算式(16)可得

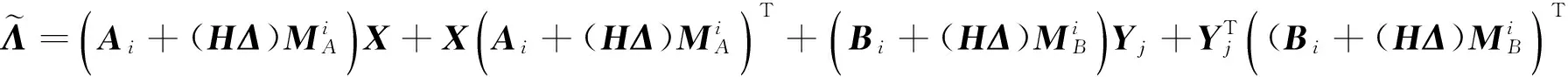
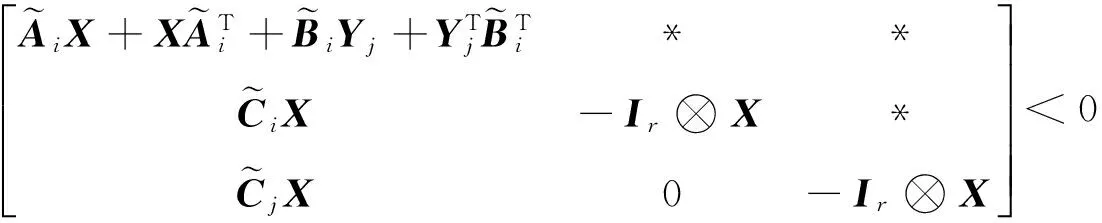
(17)
由式(17)和引理3可得闭环系统(9)是随机渐近稳定的.

3 数值实例




利用蒙特卡洛仿真思想,采用离散化方法[9]验证定理的结果.考虑一些仿真的初始参数:x1(0)=3,x2(0)=-2,仿真区间t∈[0,T],T=6.扰动变量δt=T/N,N=27,步长Δt=Rδt,R=2.图1和图2是系统分别沿着20条和50条Wiener过程路径的响应曲线,以及它们沿这些路径的均值,由图1和图2可知,闭环系统(9)是随机渐近稳定的.
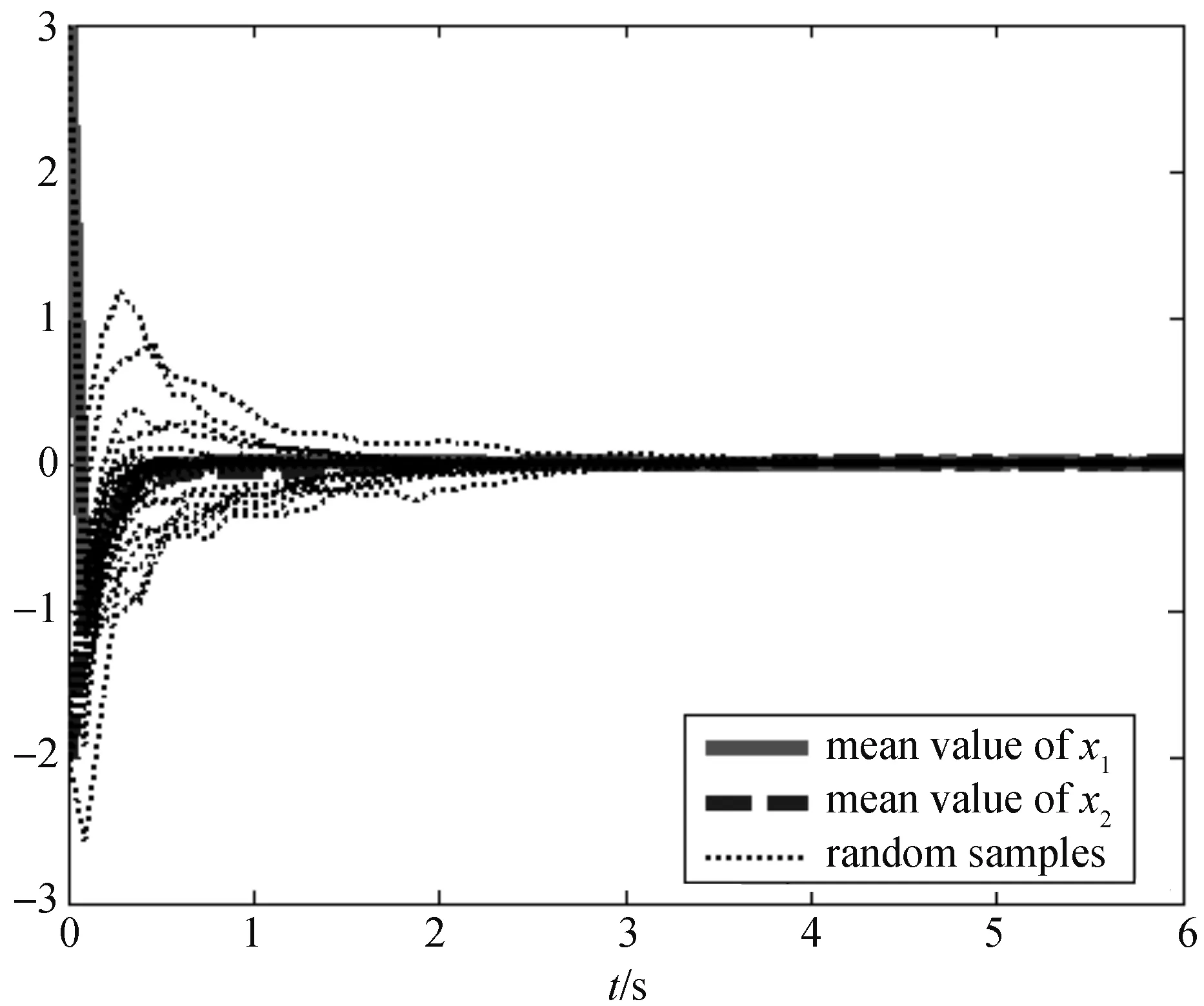
图1 x1和x2沿着20条Wiener过程的状态响应
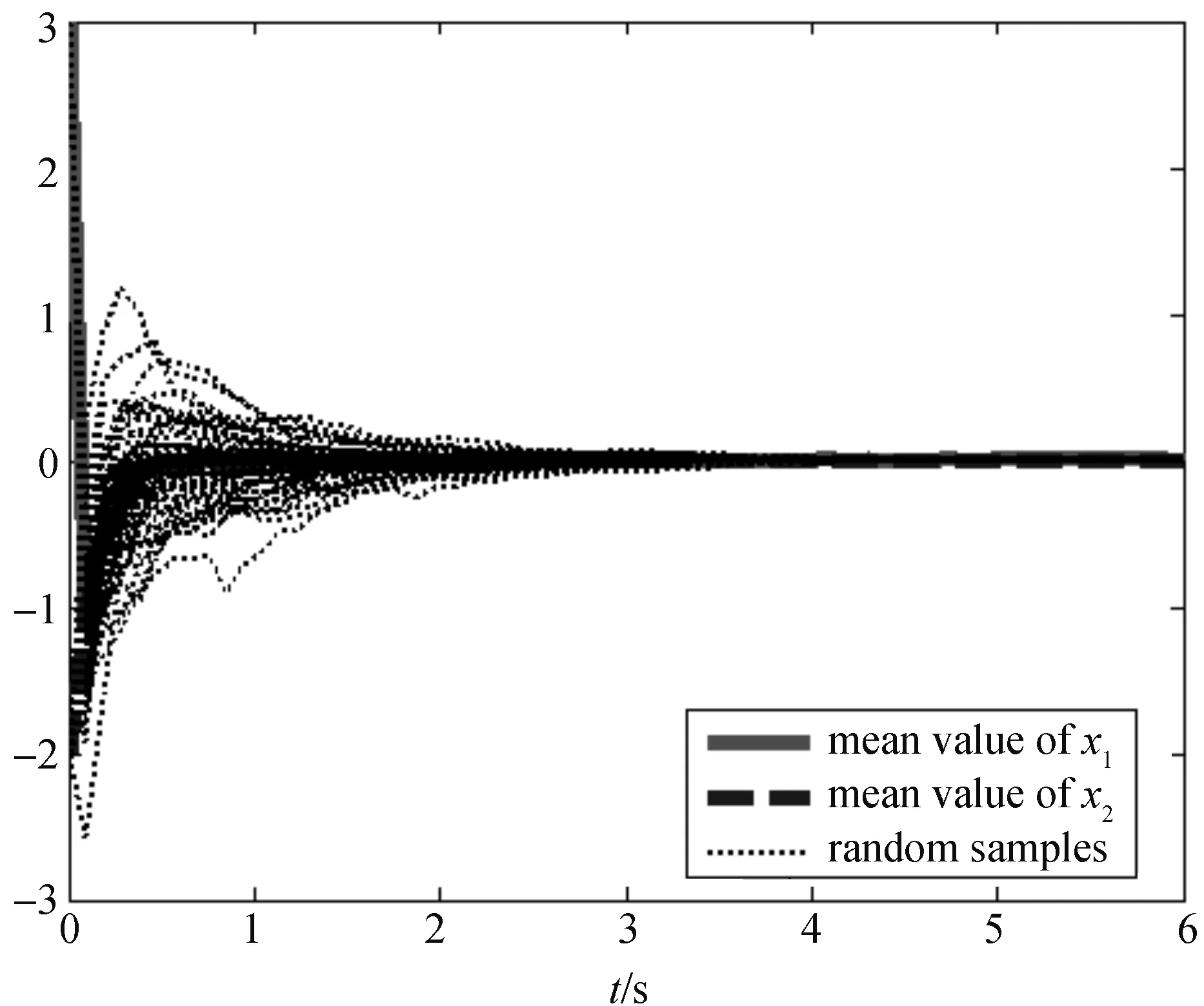
图2 x1和x2沿着50条Wiener过程的状态响应
4 结束语
本文针对区间二型带有多Wiener过程的参数不确定的系统,设计了使系统随机渐近稳定的状态反馈控制器.通过引入Kronecker积以及矩阵不等式的分解技巧,解决了多Wiener过程的随机扰动和具有线性分式结构的参数不确定的难题.最后给出仿真实例验证所设计方法的可行性.
[1]ZADEHLA.TheconceptofalinguisticvariableanditsapplicationtoapproximateReasoning-I[J].InformationSciences,1975,8(3):199-249.
[2]MENDELJM,JOHNRIB.Type-2fuzzysetsmadesimple[J].FuzzySystems,IEEETransactionson,2002,10(2):117-127.
[3]LAMHK,LIHY,DETERSC,etal.Controldesignforintervaltype-2fuzzysystemsunderimperfectpremisematching[J].IndustrialElectronics,IEEETransactionson, 2014,61(2):956-968.
[4]ZHAOT,XIAOJ.Anewintervaltype-2fuzzycontrollerforstabilizationofintervaltype-2T-Sfuzzysystems[J].JournaloftheFranklinInstitute,2015,352(4):1627-1648.
[5]ZHOUSS,RENWY,LAMJ.StabilizationforT-Smodelbaseduncertainstochasticsystems[J].InformationSciences,2011,181(4):779-791.
[6]ZHANGLL,ZHOUSS.StabilizationforaclassofstochasticT-Sfuzzysystemswithdifferentpremises[C]//第25届中国控制与决策会议论文集.沈阳:控制与决策,2013:2483-2486.
[7]ZHOUSS,FENGG,LAMJ,etal.RobustH∞controlfordiscrete-timefuzzysystemsviabasis-dependentLyapunovfunctions[J].InformationSciences,2005,174(3):197-217.
[8]张彪,周绍生.区间二型随机模糊系统的控制设计[J].杭州电子科技大学学报,2015,35(2): 70-74.
[9]HIGHAMDJ.AnalgorithmicintroductiontoNumericalsimulationofstochasticdifferentialequations[J].SiamReview,2001,43(3):525-546.
Control Design for Interval Type-2 Uncertain Stochastic Fuzzy Systems
CHEN Yuping1, ZHOU Shaosheng2
(1.SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China;2.SchoolofAutomation,HangzhouDianziUniversity,HangzhouZhejiang310018,China)
This paper is considered with the controller design problem for interval type-2 uncertain Itstochastic fuzzy systems driven by a multidimensional Wiener process. By employing a stochastic Lyapunov approach and inequality techniques, a sufficiency conditions for stochastic stability of the close-loop systems are given. A matrix decomposition technique based is effective in dealing with parameter uncertainties. Finally, the stochastic stability of the resulting closed-loop system is illustrated via a simulation example.
interval type-2 fuzzy system; stochastic system; uncertain
10.13954/j.cnki.hdu.2016.05.009
2016-01-15
国家自然科学基金资助项目(61273093);浙江省自然科学基金重点资助项目(LZ12F03001)
陈玉平(1992-),女,河南周口人,硕士研究生,先进控制理论.通信作者:周绍生教授,E-mail:sszhou@hdu.edu.cn.
TP273
A
1001-9146(2016)05-0047-05

