抛物线的变换

□刘顿

抛物线的变换

□刘顿

二次函数是中考重要而常见的考点，且大多出现在综合题和压轴题中，其中有关抛物线的变换更是频频亮相，现归类说明，供参考！

一、抛物线的旋转

例1（2016·菏泽）如图1，一段抛物线：y=-x（x-2）（0≤x≤2）记为C1，它与x轴交于两点O、A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；……如此进行下去，直至得到C6.若点P（11，m）在第6段抛物线C6上，则m=________.

图1

分析：将抛物线C1通过配方法求出顶点坐标并求出抛物线与x轴的交点坐标，由旋转的性质可以知道C1与C2的顶点到x轴的距离相等，且OA1=A1A2，照此类推可以知道点P（11，m）为抛物线C6的顶点，从而得到结果.

解：∵y=-x（x-2）（0≤x≤2），

∴配方，得y=-（x-1）2+1（0≤x≤2），

∴顶点坐标为（1，1），

∴A1坐标为（2，0），

∵C2由C1旋转得到，

∴OA1=A1A2，

即C2顶点坐标为（3，-1），A2（4，0）；照此类推可知，C3顶点坐标为（5，1），A3（6，0）；C4顶点坐标为（7，-1），A4（8，0）；C5顶点坐标为（9，1），A5（10，0）；C6顶点坐标为（11，-1），A6（12，0），∴m=-1.

点评：解题的关键是求出抛物线的顶点坐标.

二、抛物线的平移

例2（2016·金华）在平面直角坐标系中，点O为原点，平行于x轴的直线与抛物线L：y=ax2相交于A、B两点（点B在第一象限），点D在AB的延长线上.

（1）已知a=1，点B的纵坐标为2.

①如图2，向右平移抛物线L使该抛物线过点B，与AB的延长线交于点C，求AC的长.

图2

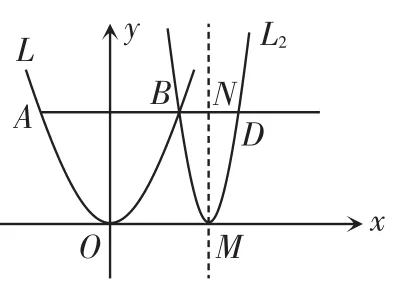
图3

（2）如图4，若BD=AB，过O、B、D三点的抛物线L3，顶点为P，对应函数的二次项系数为a3，过点P作PE∥x轴，交抛物线L于E、F两点，求的值，并直接写出的值.

图4

分析：（1）①根据函数解析式求出点A、B的坐标，进而求出AC的长；②作抛物线L2的对称轴与AD相交于点N，根据抛物线的轴对称性求出OM，利用待定系数法求出抛物线的函数表达式.

（2）过点B作BK⊥x轴于点K，设OK=t，得到OG=4t，利用待定系数法求出抛物线的函数表达式，根据抛物线过点B（t，at2），求出的值，根据抛物线上点的坐标特征求出的值.

解：（1）①二次函数y=ax2，

当y=2时，2=x2，

∵平移得到的抛物线L1经过点

②作抛物线L2的对称轴与AD相交于点N，如图3，根据抛物线的轴对称性，得

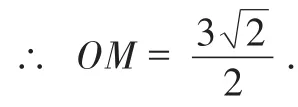
设抛物线L2的函数表达式为

解得a=4.

∴抛物线L2的函数表达式为

（2）如图4，抛物线L3与x轴交于点G，其对称轴与x轴交于点Q，过点B作BK⊥x轴于点K.

设OK=t，则AB=BD=2t，点B的坐标为（t，at2），根据抛物线的轴对称性，得OQ=2t，OG=2OQ=4t.

设抛物线L3的函数表达式为y=a3x（x-4t），

∵该抛物线过点B（t，at2），

∴at2=a3t（t-4t），

由题意得，点P的坐标为（2t，-4a3t2），则-4a3t2=ax2，

点评：灵活运用待定系数法求

出函数解析式，掌握抛物线的对称性、正确理解抛物线上点的坐标特征是解题的关键.

三、抛物线的翻折

例3（2016·宜宾）如图5，已知二次函数y1=ax2+bx过（-2，4）、（-4，4）两点.

图5

（1）求二次函数y1的解析式.

（2）将y1沿x轴翻折，再向右平移2个单位，得到抛物线y2，直线y= m（m＞0）交y2于M、N两点，求线段MN的长度（用含m的代数式表示）.

（3）在（2）的条件下，y1、y2交于A、B两点，如果直线y=m与y1、y2的图象形成的封闭曲线交于C、D两点（C在左侧），直线y=-m与y1、y2的图象形成的封闭曲线交于E、F两点（E在左侧），求证：四边形CEFD是平行四边形.

分析：（1）根据待定系数法即可解决问题.

（2）利用图形翻折的原理，先求出抛物线y2的顶点坐标，再求出其解析式，利用方程组以及根与系数关系即可求出MN.

（3）用类似（2）的方法分别求出CD、EF，即可解决问题.

解：（1）∵二次函数y1=ax2+ bx过（-2，4）、（-4，4）两点，

∴二次函数y1的解析式为

∵将y1沿x轴翻折，再向右平移2个单位，得到抛物线y2，则抛物线y2的顶点坐标是

∴抛物线y2为

消去y并整理得

x2+2x-8-2m=0，

设x1、x2是它的两个根，

则x1+x2=-2，x1x2=-8-2m，

设其两个根为x1，x2，

则CD=|x1-x2|

设其两个根为x1，x2，

则EF=|x1-x2|

即EF=CD，又EF∥CD，

故四边形CEFD是平行四边形.

点评：本题涉及二次函数、根与系数关系、平行四边形的判定等知识，解题的关键是灵活应用这些知识解决问题，记住公式|x1-x2|=属于中考压轴题.