导管架海洋平台失效路径分析及连续倒塌机制

林 红，陈国明，朱本瑞，刘红兵，张 禹，李 萍

（1.中国石油大学海洋油气装备与安全技术研究中心，山东青岛266580；2.中国石油大学储运与建筑工程学院，山东青岛266580；3.天津大学建筑工程学院，天津300072）

导管架海洋平台失效路径分析及连续倒塌机制

林 红1，2，陈国明1，朱本瑞3，刘红兵1，张 禹2，李 萍2

（1.中国石油大学海洋油气装备与安全技术研究中心，山东青岛266580；2.中国石油大学储运与建筑工程学院，山东青岛266580；3.天津大学建筑工程学院，天津300072）

针对突发事件下导管架平台“局部破坏”可能引发的连续倒塌现象，建立一种针对导管架平台结构的失效路径搜索及概率评估流程，采用逐步施加增量载荷的方法，并结合广义承力比准则，充分考虑失效过程中单元内应力的变化及候选失效单元的不确定性和外部载荷的随机性，并通过模拟示例获得平台可能发生的事故树，从而确定最可能发生的失效顺序。针对具体失效路径，引入备用荷载路径方法（ALP方法），研究倒塌过程中平台结构的力学分布特性和状态变化规律，分析构件失效后的平台剩余系统的动力效应和内力重分布规律，从而揭示平台结构的连续倒塌机制。结果表明：某桩腿单元突发失效后，失效单元上方的水平撑杆通过塑性铰机制成为新的竖向传力路径；相邻桩腿由于严重的内力重分布现象成为薄弱环节，易发生屈曲失效。

导管架平台；失效路径；连续倒塌；内力重分布；备用荷载路径方法

在长期复杂的服役环境中，海洋平台结构会面临各种突发事件［1］，如构件断裂、局部火灾爆炸、船舶撞击、重物坠落等，由于突发事件造成海洋石油平台严重事故多有发生［2-4］。针对各种突发灾害后平台结构的损伤及承载能力分析，研究者开展了广泛的研究［5-7］。然而，上述研究大都局限于平台在失效之前的响应分析，并未考虑可能引发的连续倒塌［8］现象，无法描述连续倒塌过程中平台结构的力学分布特性和状态变化。美国GSA［9］和DoD［10］规范中推荐采用备用荷载路径方法（alternative load path method），即ALP方法，分析由于局部破坏引发的蔓延过程。然而，目前该方法主要用于建筑类结构，鲜有文献采用ALP方法对海洋平台倒塌过程进行具体分析。另一方面，由于载荷的复杂性及导管架平台结构的高度冗余性，平台有可能出现多种倒塌失效模式，且每个失效模式又有不同的失效路径。若能识别出平台的失效路径，则有可能避免倒塌，或者可以选择某种合理的倒塌顺序，从而减少人员生命和财产损失。对于导管架平台失效路径分析而言，研究的难点集中在失效构件的识别及路径失效概率计算两方面。目前，海洋平台失效路径搜寻的常用方法有增量载荷法、分支限界法和β-解链法，其中增量载荷法［11］的优点是计算量较小，且可以利用已有的结构分析软件如ANSYS等，这决定了它具有广泛的实用价值。基于此，笔者提出一种针对导管架平台结构的失效路径搜索及概率评估流程，结合广义承力比与增量载荷方法，搜索平台结构的可能失效路径；进而引入备用荷载路径（ALP）方法，揭示平台结构的连续倒塌机制，从而为抗倒塌设计及现役平台的重评估提供理论依据。

1 平台连续倒塌失效路径搜索与概率评估方法

1.1 失效路径搜索的广义承力比准则

由n个单元r1，r2，…，rn构成的结构体系中，依次施加增量载荷s1，…，sj-1，导致r1，r2，…，rj-1共j-1个单元已相继失效。继续施加增量载荷sj，在失效历程的第j阶段，对于结构单元ri，有ri∈（r1，r2，…，rn）且ri∉（r1，r2，…，rj-1），其广义承力比定义为

式中，Ri为单元ri的承载强度；为对由（n+1-j）个残余单元组成的结构系统在外载荷作用处施加单位广义载荷而求得的单元ri的内应力。

1.2 基于增量载荷法的失效路径概率评估

对于导管架海洋平台这种高冗余度空间结构，根据上述承力比准则将有可能搜索出非常多条失效路径，还需要对每条失效路径的发生概率进行评估，从而确定出最有可能发生的失效路径，即主要失效路径。对于n个元件组成的系统，若有m个元件失效，并记aij=a（j）i，根据增量加载理论，结构系统的加载过程可以表示为

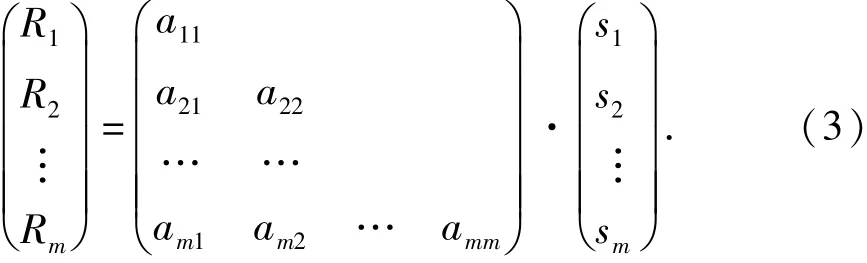
式中，aij表示随机变量sj为单位载荷时单元ri所分配的内力。

由方程（3）可反解出载荷：

式中，am为由（n+1-m）个残余单元组成的结构系统在外载Ti作用处施加单位广义载荷而求得m单元的内应力；q为外载总数。其中外载S随工况的不同而异。

从而平台系统的安全余量方程为

则对于第i条失效路径来说，其可靠度可表示为

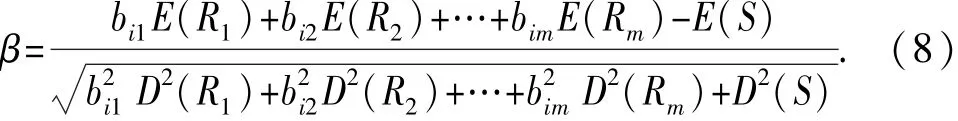
式中，E（.）和D（.）分别表示括号里内容的期望和标准差。

bi1，…，bim可由式（6）得到，则该条失效路径对应的失效概率为

可通过一次可靠度（FORM）或二次可靠度（SORM）方法［14］进行计算。

图1给出了导管架平台失效路径搜索及失效概率计算的流程。

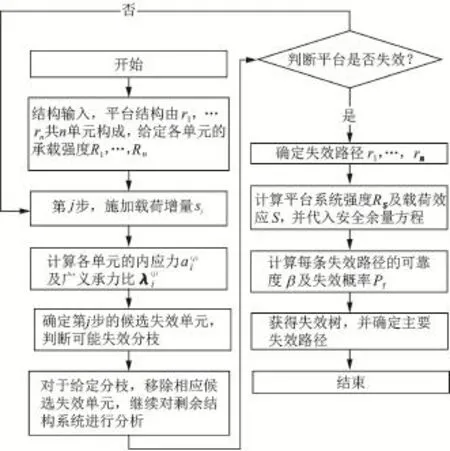
图1 失效路径搜索及失效概率计算流程Fig.1 Flow diagram of failure path identification and failure probability calculation

2 导管架有限元模型与倒塌失效路径评估结果

2.1 导管架平台模型及环境参数

以四桩腿型导管架模型为研究对象，导管架共分4层。采用ANSYS软件建立导管架的有限元模型，模型、桩腿编号及单元编号如图2所示。设平台导管架在泥面以下6倍桩径处固定，结构承受自重及上部甲板重力，且在水平面处受到沿X方向的冰载荷作用，其中静冰力的计算采用K-A公式［15］：

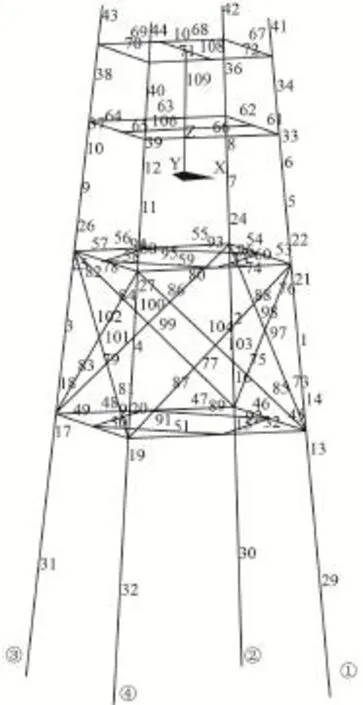
图2 导管架有限元模型及单元编号、桩腿编号Fig.2 FE model of jacket platform and element number，leg number

其中，形状系数m取0.9，接触系数K取0.25，局部挤压系数I取2.5，桩腿直径D取1.35 m，海冰抗压强度σc取2.13 MPa。约界参数取0.95。

2.2 导管架平台失效路径计算结果

考虑到桩腿构件是导管架结构中的关键部位，在选择第一步失效单元时，假定①号桩腿上的6号单元（该单元位于静水线上）被冰载荷撞击而发生破坏，即认为导管架平台为含有初始损伤的结构。根据1.1节的失效路径分析过程，获得该平台的失效树如图3所示。该失效树有2个大分支，共含有6条失效路径，且各条路径均含有9个失效单元。

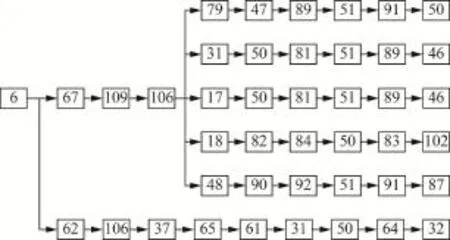
图3 导管架平台结构的失效树Fig.3 Failure tree of jacket platform

计算出上述各条失效路径的失效概率分别为1.98×10-2、4.5×10-2、4.6×10-12、9.36×10-21、2.17× 10-25、1.27×10-11。可见，第1和第2条失效路径为主要失效路径；第3和第6条路径为次要失效路径；而第4和第5条路径的失效概率非常小，可视为无效路径。由第2条失效路径可知，该导管架结构最可能发生的失效顺序是：第2、3层间的桩腿单元初始破坏→上方相邻的第1、2层水平撑杆破坏→最底层的桩腿单元破坏→最下层横撑和斜撑杆破坏→平台整体失效。

约界参数的不同将会对计算结果产生一定影响，重新选取其值为0.98、0.90、0.85进行计算。结果表明，约界参数的影响主要体现在两方面：在结构失效树生成方面，减小约界参数会极大地增加失效路径；而在失效概率方面，由于失效路径大大增加，开始出现较多的无效失效路径。对于本算例约界参数取0.95是合适的，且上述最可能发生的失效路径与工程实际相符合。

3 导管架平台连续倒塌机制

对于上述最有可能发生的具体失效路径来说，其失效过程是由于初始构件的突然失效，引起周围构件的动态应力超出了其承载能力，致使周围构件失效，从而导致额外的动态内部力的传递，直到剩余结构重新稳定或倒塌［16］。实质上，平台结构的重要构件发生初始破坏后，将造成平台整体结构发生突变而振动，从而产生惯性力，因此结构连续倒塌是一个动力过程［17］。有必要研究构件初始失效后引起的动力效应，并进一步分析平台剩余系统的内力重分布规律，从而揭示平台结构的连续倒塌机制。

3.1 导管架连续倒塌动态效应分析

在ALP分析过程中，利用瞬时加载法［18］进行构件破坏后剩余平台系统的动力分析。首先对移除单元后的导管架结构进行模态分析，提取模态计算的结果，计算结构的质量阻尼系数α和刚度阻尼系数β为

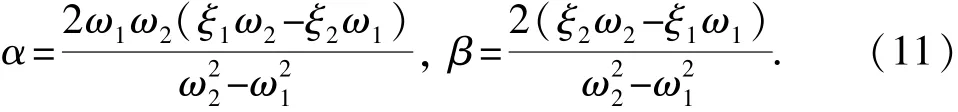
式中，ω1、ω2为结构的一阶、二阶固有频率；ξ1、ξ2为其相应的结构振型阻尼比，海上导管架平台阻尼比一般为0.02～0.05，故可取ξ1=ξ2=0.03［17］。

计算出本结构的质量阻尼与刚度阻尼分别为0.86834和0.0010345。在模拟单元失效过程中，失效时间tf是一个关键因素，为了分析失效时间对动态分析结果的影响，将失效时间tf分别取为tf=T/ 10=0.0219 s，tf=T/2=0.109 s和tf=T=0.219 s。

对于①号桩腿上6号单元突然失效后平台的振动过程进行了分析。图4给出了各种失效时间下失效节点的竖向位移时程曲线。可见，失效时间越短，产生的振动效应越明显，振动幅值越大，且最大位移响应越大。当失效时间为0.0219 s时，产生的最大竖向位移为-28.7 cm，而失效时间为0.21 9 s时最大竖向位移仅为-18.5 cm，变化幅度达到55.1%。同时随着失效时间增大，出现最大竖向位移的时间逐渐向后推迟，由0.109 s至0.198、0.274 s。构件失效的响应时间越短，将对剩余结构产生越不利的影响。

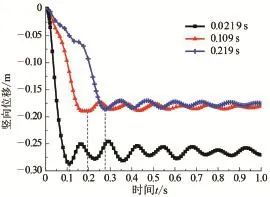
图4 失效端弯矩及竖向位移时程曲线Fig.4 Vertical displacements of failure node with different response time

3.2 竖向传力机制及传力路径形成

对平台承受的载荷进行简化处理，仅考虑导管架承受的竖向载荷，包括导管架及上方甲板部分的自重载荷及可能发生的甲板上浪载荷，并将竖向载荷均匀作用在导管架顶端的4个桩腿单元上。假定①号桩腿上6号单元失效，图5为完好平台结构以及剩余导管架结构的轴力，表1为各桩腿单元轴力变化。

①号桩腿上与6号单元直接相连的33号和5号桩腿单元的轴力几乎降为0，且6号单元下方的其他桩腿单元轴力也大幅减少，而只有最顶层处41号桩腿单元受影响较小。由此可知，移除桩腿上某个单元后，与其直接相连及其下方的桩腿单元几乎失去支撑作用。这表明，由于桩腿上某个构件的失效，切断了该条桩腿的竖向传力路径，因此为保证剩余结构稳定，必然要重新寻求新的传力路径。

为寻求新的传力路径，进一步分析②号与④号桩腿上各单元的轴力变化。由于对称性，②号与④号桩腿上轴力分布及变化情况大致相同，列出②号桩腿上轴力变化情况见表1。可见，当①号桩腿上6号单元移除后，②号与④号这两个桩腿上各单元的轴力大幅增加，且这两个桩腿上与移除单元的高度越接近的单元其内力的增幅越大，几乎增至原来的2倍；正是由于这些桩腿单元受压过大，剩余平台结构易于在此处发生屈曲失效，因此必须引起重视。

相反，③号桩腿上各单元所受压力则不同程度下降，最大降幅降为约为原来的37%，见表1。上述结果表明，当①号桩腿上6号单元移除后，原来应该由①号桩腿上单元承担的竖向载荷传递至距离较近的②号与④号桩腿单元，降低了距离较远的③号桩腿的承压作用。

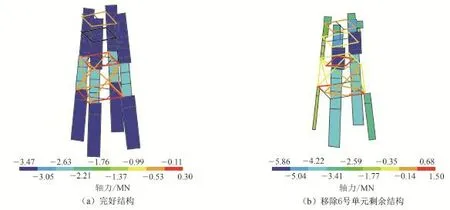
图5 完好结构轴力及移除6号单元剩余结构轴力Fig.5 Axial force distributions of intact structure and after removing element 6

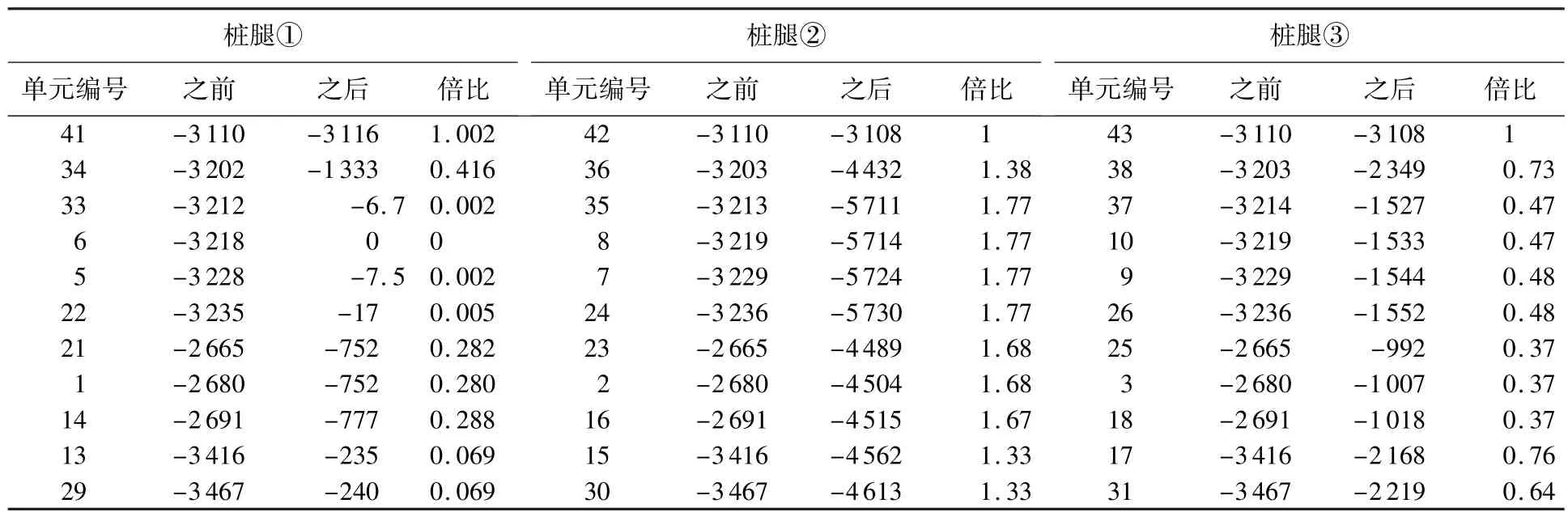
表1 移除6号单元前后桩腿①，②及③上各单元轴力变化Table 1 Axial forces of elements in pile legs①，②and③before and after removing element 6　kN

3.3 横向构件的承力梁机制

进一步分析各层横撑单元轴力的变化，见表2。移除①号桩腿上6号单元后，其上方紧邻的第二层内各横撑单元的轴力发生了显著变化，除了与6号单元距离较远的63、64、65号单元仅在数值上发生较小变化外，其他各紧密相连单元的轴力不仅数值显著变大，且均由受拉状态转变为受压状态，其倍比分别达到了8.07倍至33.8倍，这些轴力突变的横撑杆件成为剩余结构的薄弱环节。这表明，①号桩腿上6号单元移除后，位于失效单元上方的横撑单元将成为新的传力路径中的一个重要环节，这个结论与2.2节分析的失效顺序相吻合。

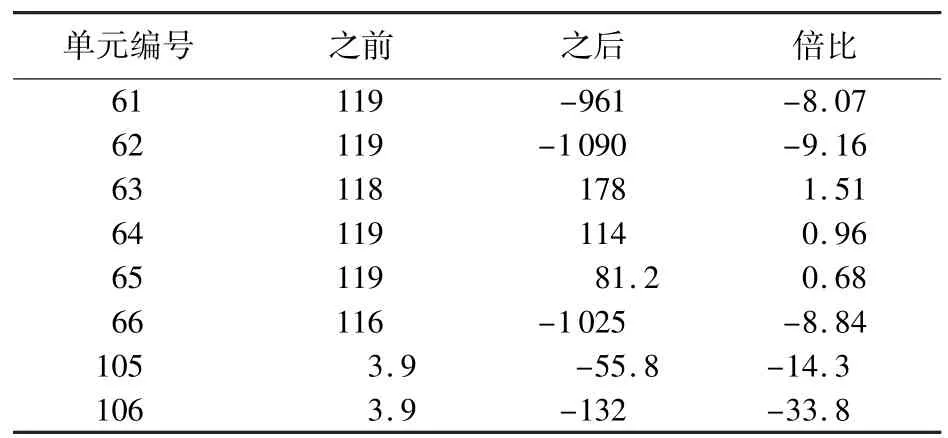
表2 移除6号单元前后第2层各横撑单元轴力变化Table 2 Axial forces of horizontal elements at the second layer before and after removing element 6　kN

当桩腿上单元移除后剩余结构的弯矩也将出现重分布现象，见图6。移除①号桩腿上6号单元后，位于该单元上方第一和第二层内各水平撑杆的端部弯矩大幅增加，形成承力梁机制，以承担相应的竖向载荷。这里仅列出其中变化幅值较大的两个单元（66号和67号横撑单元）的弯矩值变化情况，见表3。同时发现，在水平撑杆的两端点弯矩数值分别呈现出一正一负的现象，即弯矩在撑杆中间位置发生变号，这说明移除桩腿单元上方的水平撑杆在局部区域弯矩变化非常剧烈，成为剩余结构的受力薄弱部位。

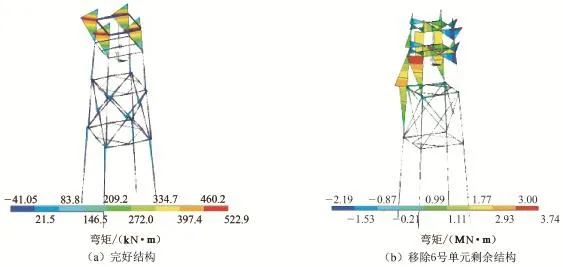
图6 完好结构弯矩和移除6号单元剩余结构弯矩Fig.6 Bending moment distributions of intact structure and after removing element 6

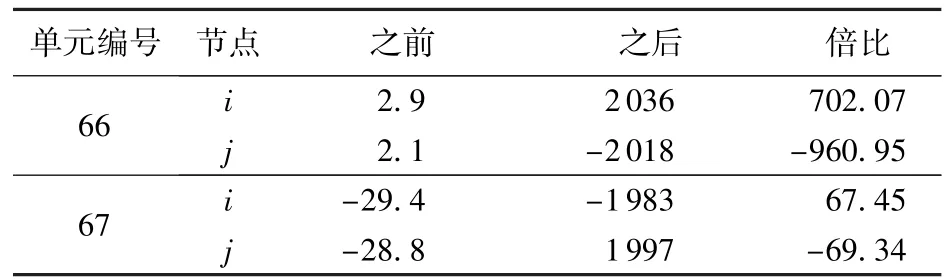
表3 移除6号单元前后第3层横撑单元弯矩变化Table 3 Bending moments of horizontal members in the third layer before and after removing element 6 kN.m

为进一步揭示承力梁机制的形成过程，绘制了6号单元移除后66号横撑杆单元左端i节点的弯矩及节点竖向位移的局部时程曲线，见图7。

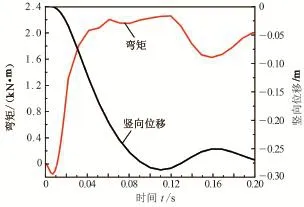
图7失效节点弯矩及竖向位移时程曲线Fig.7 Vertical displacement and bending moment of failure node

由图7可见，在0.04 s之前，随着i节点位移的增大弯矩也快速增大；在0.04～0.11 s之间，随着i节点位移的进一步增大而弯矩几乎不再发生增长，弯矩数值一直保持在2200 kN.m，这个现象表明在该横撑单元左端形成了塑性铰；随后，节点位移方向发生反向，即当结构开始转为向上振动时，该处弯矩开始减小；这一振动过程逐渐衰弱，并最终趋于稳定。

3.4 构件局部破坏位置影响

大量有限元算例表明，移除水平撑杆、斜撑杆单元对平台内力的影响非常小，移除后剩余平台系统的内力重分布现象并不明显，这表明仅在竖向载荷作用下上述类型的撑杆不是引起导管架平台发生连续倒塌的关键构件。

移除不同高度的桩腿单元，剩余平台的内力重分布规律基本一致，均表现出相邻桩腿构件受压增大及上方相邻撑杆形成塑性铰的传力机制；且移除桩腿单元的位置越低，内力重分布现象越显著。这表明仅在竖向载荷作用下最底层的桩腿单元是引起导管架平台发生连续倒塌的最关键单元，在进行平台结构倒塌预防与控制时，可采用灌浆或卡箍等措施对该弱点进行加固。

4 结 论

（1）采用逐步施加增量载荷的方法及广义承力比准则，并充分考虑失效过程中单元内应力的变化及候选失效单元的不确定性和外部载荷的随机性，得到导管架平台的失效路径搜寻与失效概率的计算流程。最可能的失效顺序为第2、3层间的桩腿单元初始破坏→上方相邻的第1、2层水平撑杆破坏→最底层的桩腿单元破坏→最下层横撑和斜撑杆破坏→平台整体失效。

（2）构件的失效时间越短，产生的振动效应越明显，振动幅值越大，且最大位移响应越大。即构件失效响应时间越短，将对剩余结构产生越不利的影响。

（3）仅在竖向载荷作用下桩腿单元突然失效后，相邻桩腿上同一高度的单元容易发生屈曲失效，水平撑杆通过塑性铰机制成为竖向传力路径；而水平撑杆、斜撑杆单元失效后，剩余平台系统的内力重分布现象并不明显，这些构件的失效不容易引发平台的连续倒塌。

［1］ GERHARD E.Assessment of existing offshore structures for life extension［D］.Norway：University of Stavanger，2005.

［2］ WOAD.Worldwide offshore accident databank［R］.Oslo：Det Norske Veritas，1996.

［3］ AMDAHL J.Structural response to accidental loads［R］. Trondheim：Norwegian University of Science and Technology，1999.

［4］ Det Norske Veritas.Accident statistics for fixed offshore units on the UK continental shelf 1980—2005［R］.Hovik：Health and Safety Executive，2007.

［5］ 朱本瑞，陈国明，林红，等.极端波浪载荷下导管架平台抗倒塌性能评估［J］.中国石油大学学报（自然科学版），2014，38（3）：135-141. ZHU Benrui，CHEN Guoming，LIN Hong，et al.Anticollapse performance assessment of jacket offshore platforms in extreme storm waves［J］.Journal of China University of Petroleum（Edition of Natural Science），2014，38（3）：135-141.

［6］ 鲍莹斌，李润培，顾永宁.船舶与海洋平台碰撞的动塑性分析［J］.上海交通大学学报，1997，31（7）：40-44. BAO Yingbin，LI Runpei，GU Yongning.Dynamic plastic analysis of ship-platform collision［J］.Journal of Shanghai Jiaotong University，1997，31（7）：40-44.

［7］ 宋剑，金伟良，何勇，等.火灾作用下海洋平台结构响应分析［J］.海洋工程，2006，24（2）：21-28. SONG Jian，JIN Weiliang，HE Yong，et al.Structural response analysis of offshore platform subjected to fire［J］.The Ocean Engineering，2006，24（2）：21-28.

［8］ 胡晓斌，钱稼茹.结构连续倒塌分析与设计方法综述［J］.建筑结构，2006，36（s1）：79-83. HU Xiaobin，QIAN Jiaru.Overview of analysis and design approaches for progressive collapse of structures［J］. Building Structure，2006，36（s1）：79-83.

［9］ General Service Administration.Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects：GSA2003［S］. Washington D C：US General Services Administration，2003.

［10］ Department of Defense.Design of structures to resist progressive collapse：DoD2005（UFC 4-023-03）［S］. Washington D C：Department of Defense，2010.

［11］ 杨国安，盖会明.海洋平台水下结构累积损伤失效路径的动态搜寻方法［J］.中国海洋平台，2006，21（6）：12-17. YANG Guoan，GAI Huiming.The methods for dynamically selecting main invalid routes of the undersea part of offshore platforms that is being caused by accumulating damage［J］.China Offshore Platform，2006，21（6）：12-17.

［12］ 徐格宁，杨瑞刚.约界参数CAP对大型钢结构系统可靠性分析的影响［J］.中国机械工程学报，2005，41（12）：130-134. XU Gening，YANG Ruigang.Influence of control ambit parameter CAP for reliability analysis of large type steel structures system［J］.Chinese Journal of Mechanical Engineering，2005，41（12）：130-134.

［13］ FRED M.Problems and prospects of reliability-based optimization［J］.Engineering Structures，1997，19（4）：293-301.

［14］ 贡金鑫.工程结构可靠度计算方法［M］.大连：大连理工大学出版社，2003.

［15］ 欧进萍，段忠东，肖仪清.海洋平台结构安全评定—理论、方法与应用［M］.北京：科学出版社，2003.

［16］ 吕大刚，李雁军，陈志恒.钢筋混凝土框架结构连续倒塌的竖向非线性动力分析［J］.土木建筑与环境工程，2012，34（s1）：49-53. LÜ Dagang，LI Yanjun，CHEN Zhiheng.Progressive collapse analysis of RC frame using vertical nonlinear dynamic analysis［J］.Journal of Civil，Architectural& Environmental Engineering，2012，34（s1）：49-53.

［17］ 杨冬平，陈国明.海洋平台结构连续倒塌非线性动力响应分析［J］.西安建筑科技大学学报（自然科学版），2010，42（2）：267-271. YANG Dongping，CHEN Guoming.Nonlinear dynamic response analysis of progressive collapse in offshore platform structure［J］.Journal of Xi΄an University of Architecture&Technology（Natural Science Edition），2010，42（2）：267-271.

［18］ 王铁成，刘传卿.钢框架结构动力连续倒塌分析［J］.建筑结构，2010，40（4）：5-8. WANG Tiecheng，LIU Chuanqing.Dynamic progressive collapse analysis of steel frame structure［J］.Building Structure，2010，40（4）：5-8.

（编辑 沈玉英）

Failure paths identification and progressive collapse mechanism analysis of offshore jacket platforms

LIN Hong1，2，CHEN Guoming1，ZHU Benrui3，LIU Hongbing1，ZHANG Yu2，LI Ping2
（1.Center for Offshore Engineering and Safety Technology，China University of Petroleum，Qingdao 266580，China；2.College of Pipeline and Civil Engineering in China University of Petroleum，Qingdao 266580，China；3.School of Civil Engineering，Tianjin University，Tianjin 300072，China）

In order to analyze the progressive collapse problem of jacket platforms resulted from"local failure"，a failure path searching method was presented，and a failure probability calculating process was developed by using incremental loading method，in which the uncertainty of candidate failure components and the stochasticity of external loads were considered. Through simulation，all possible failure paths were sought out，and the most likely failure sequence was identified.Then，considering a specific failure spreading path，the dynamic effects of damaged platform and the rule of internal force redistribution were studied using alternative load path（ALP）method，and the progressive collapse mechanism was revealed.The analysis results indicate that：when a leg member fails，the above horizontal brace will become the new vertical load path through the plastic hinge mechanism，and then the adjacent leg member will become a weak point due to severe internal force redistribution phenomenon，therefore the platforms are prone to buckling failure.

offshore jacket platform；failure paths；progressive collapse；internal force redistribution；alternative load path（ALP）method

TE 951

A

1673-5005（2016）01-0121-07 doi：10.3969/j.issn.1673-5005.2016.01.017

2015-05-22

国家自然科学基金项目（51209218，51579246，51509184）；青岛市应用基础研究计划项目（青年专项）（14-2-4-58-jch）；中央高校基本科研业务费专项（15CX05003A）

林红（1980-），女，副教授，博士，硕士生导师，研究方向为海洋石油工程结构力学及可靠性。E-mail：linhong_ly@126.com。

引用格式：林红，陈国明，朱本瑞，等.导管架海洋平台失效路径分析及连续倒塌机制［J］.中国石油大学学报（自然科学版），2016，40（1）：121-127.

LIN Hong，CHEN Guoming，ZHU Benrui，et al.Failure paths identification and progressive collapse mechanism analysis of offshore jacket platforms［J］.Journal of China University of Petroleum（Edition of Natural Science），2016，40（1）：121-127.