某型燃气轮机枞树形榫接结构多齿形参数优化分析

宗洪明，陶海亮，高　庆，谭春青

（1.中国科学院工程热物理研究所，北京100190；2.中国科学院大学，北京100049）

某型燃气轮机枞树形榫接结构多齿形参数优化分析

宗洪明1，2，陶海亮1，高庆1，谭春青1

（1.中国科学院工程热物理研究所，北京100190；2.中国科学院大学，北京100049）

在某型燃气轮机改型设计中发现，涡轮采用的3齿枞树形榫接结构应力集中严重，为避免榫齿出现裂纹、榫头断裂等故障，并降低峰值应力，延长使用寿命，对其形状进行优化设计。分析发现，相同的齿形参数无法获得满意的优化结果，因此，对每对榫齿采用不同的齿形参数进行2维参数化建模。通过试验设计方法，选取对最大当量应力影响较大的参数作为设计变量并进行优化。在满足约束的条件下，获得优化设计结果。结果表明：优化使最大当量应力降低19.93%，各齿应力分布更加均匀。该设计方法确实能提升榫接结构的优化潜力，对其设计与优化具有一定参考价值。

枞树形榫接结构；接触应力；优化设计；涡轮；燃气轮机

0　引言

在对某型燃气轮机进行改型设计时发现，涡轮采用的3齿枞树形榫接结构所处工况恶劣，齿间圆角半径较小，齿底圆弧应力集中严重。因此，为避免榫齿裂纹、榫头断裂等故障的发生［1］，有必要对其形状进行优化设计，降低应力水平，延长运行周期。

对于榫接结构的设计及优化，国内外展开的研究很多。Meguid等［2］利用ANSYS软件研究了形状参数及摩擦系数对榫槽应力分布的影响，发现结构参数对应力分布影响极大，而摩擦系数的影响较小；Song等［3-5］以ICAD为建模工具对典型榫接结构进行优化设计，并采用样条曲线对榫齿进行局部造型，取得了较好效果；赵海［6］利用UG软件对榫接结构进行参数化建模并分析了主要设计参数对榫接结构强度的影响；申秀丽等［7-9］对一梯形齿榫接结构进行优化设计，通过灵敏度分析选取设计变量，并利用光弹性试验证明了其优化设计的可靠性；杨敏超、孙苏亚［10］结合UG、ANSYS及Isight软件对3齿枞树形榫接结构进行了优化设计，并实现了优化流程自动化。

上述国内外学者的研究大多建立在调整单一变量而保证其他参数不变的基础上，而未考虑各参数间相互影响，得到的结果不够准确。此外，目前榫接结构的设计和优化一般建立在各对榫齿载荷均一的基础上，未考虑在实际工况下不同榫齿所受载荷不一致的特点。

针对上述2点，本文建立榫接结构参数化模型，利用试验设计方法评估各参数对峰值应力的影响，以此筛选设计变量，通过采用不同的齿形参数建模，提升优化潜力。

1　计算模型及初始设计分析

1.1参数化模型

对榫接结构进行优化，需频繁改变其几何形状，必须依靠参数化建模技术。选择一定数量且相互独立的参数，使其能够完全约束结构的形状，利用参数值改变榫接结构形状，获得不同几何形状下的应力分布，从而得到结构参数与应力之间的关系。

某型燃气轮机所采用的3齿枞树形榫接结构如图1、2所示。图中从上至下为第1、2、3齿，其特征参数包括基本参数和齿形参数，该榫接结构采用圆弧形齿的设计形式以减少应力集中，3对齿的齿形参数一致。

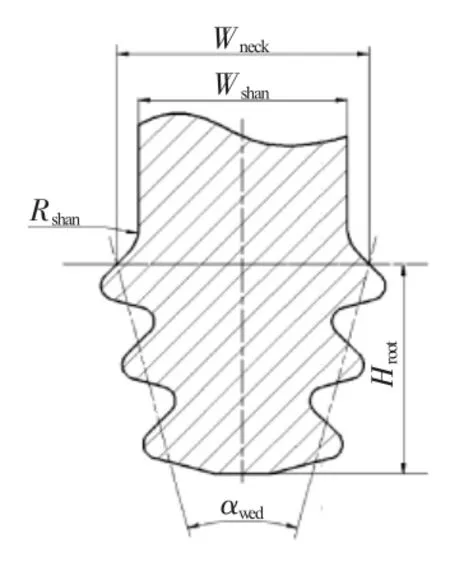
图1　枞树形榫头几何参数

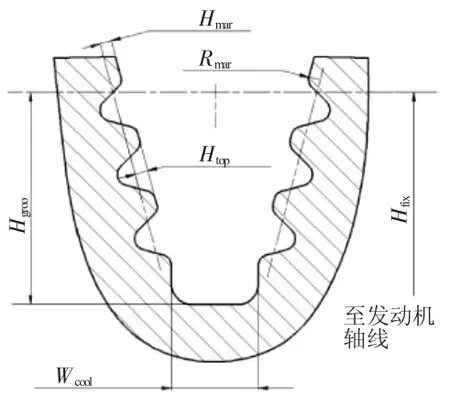
图2　枞树形榫槽几何参数

为保证优化效果，采用不同的齿形参数对每对榫齿进行造型。由于每对榫齿具有几何相似性，这里仅对1对齿的位置约束关系进行分析，如图3所示。图中A～L为每对榫齿的关键点，通过这些关键点位置使每对榫齿满足以下几何约束：（1）确定A点位置，并由此绘制榫齿上侧面，以保证榫头与榫槽始终啮合；（2）榫头和榫槽的齿厚之和小于齿距，以保证二者间具有一定的间隙；（3）对圆角处B、F及K、E关键点的位置进行约束，避免榫头与榫槽间发生干涉；（4）对榫齿自身的关键点进行约束，如I点应在J点之上，避免榫齿形状畸形。以上4点可以保证绘制出合理的榫接结构。文中所涉及各结构参数的含义见表1。

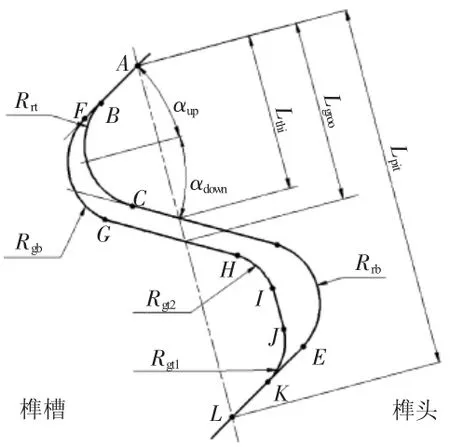
图3　榫齿几何参数

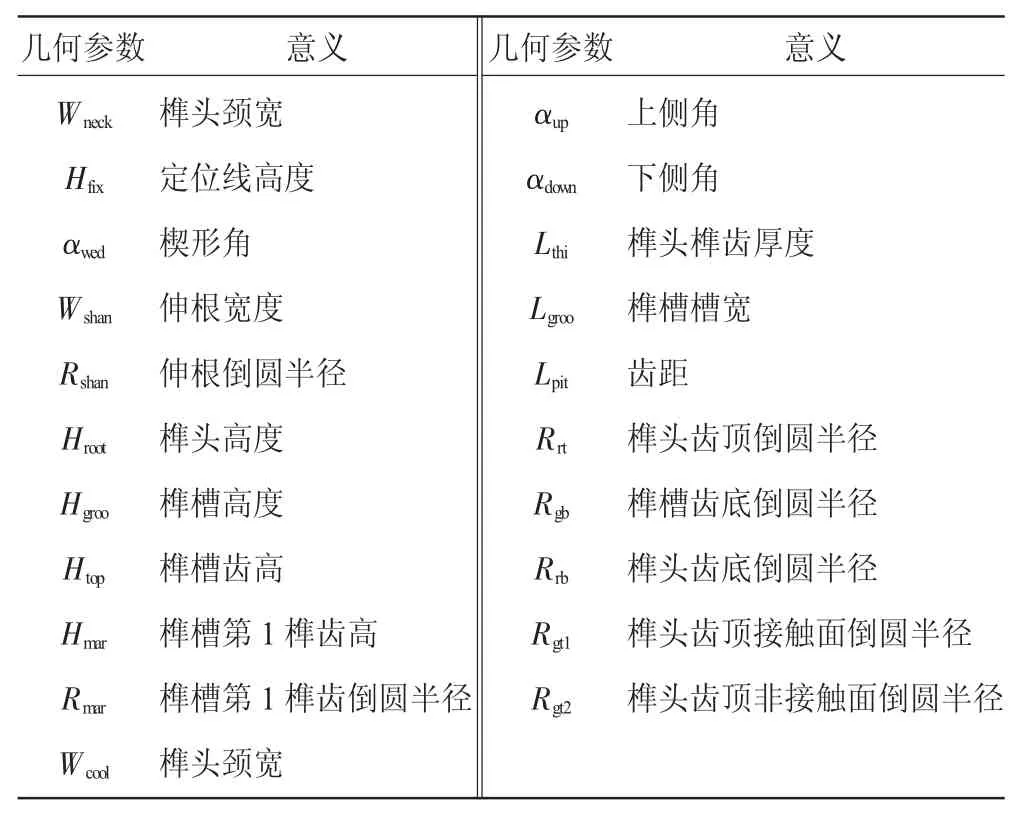
表1　榫接结构几何参数及意义

1.2有限元模型

由于榫接结构的应力求解涉及接触的非线性问题［11-12］，难以得到解析解，通常采用光弹性实验法［13］和有限元方法［14］获得接触应力分布。相较于光弹性实验法，有限元方法更易于实现，且随着该方法的不断完善，利用其进行应力分析也越发准确和普遍。因此，本文利用ANSYS软件获得榫接结构内部的应力分布，分析各结构参数的影响并进行优化设计。

在高温燃气中的榫接结构，温度载荷对应力影响很大。Ali等［15］利用MARC软件对2维榫接结构在机械-热耦合载荷下1个工作周期内的应力状况进行了研究。结果表明：当考虑温度载荷时，最大应力增大了15%但位置不变，说明主要载荷为离心力，因此本文仅考虑离心力载荷进行优化设计。

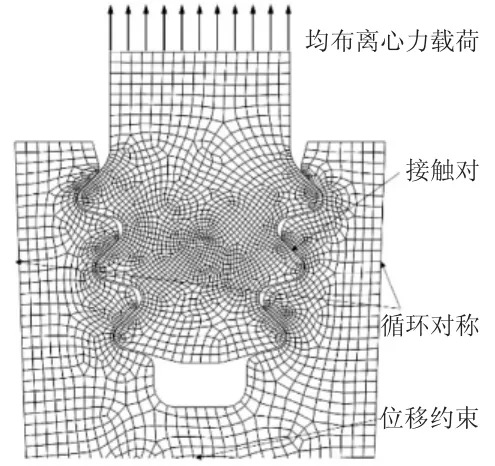
图4　2维模型网格划分、接触设置及边界条件

在叶片离心力作用下，由于榫接结构的轴向变形较小，可等效为2维平面应变模型［8］。其网格划分、加载情况及约束条件如图4所示。采用Plane183平面应变单元进行网格划分；在图示齿面位置设置接触条件，为保证接触压力计算的精度，对接触面进行网格加密处理，采用扩增拉格朗日法进行接触面非线性计算；为减小计算量，截取1/92模型进行分析，在两侧施加循环对称条件；在伸根处施加均布拉应力模拟叶片的离心力作用。叶片及轮盘材料性能见表2。

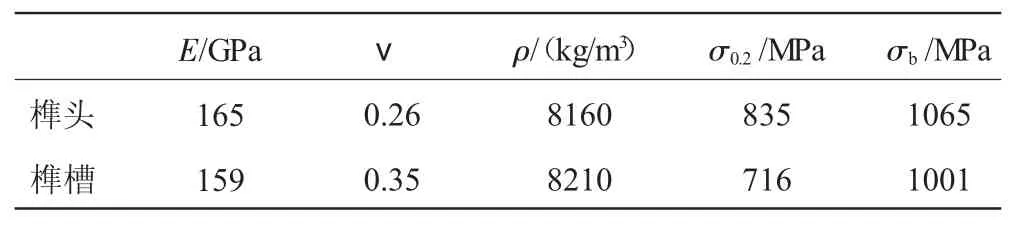
表2　榫头/榫槽材料性质

1.3初始设计分析

榫接结构通过接触将叶片离心力传递给轮盘，因此接触压力的分布对榫头、榫槽的应力分布影响很大。初始设计接触压力分布如图5所示。从图中可见，最大接触压力出现在第1齿靠近伸根处，这是由于在初始设计中，该处的接触长度较第2、3齿的都短，使得接触压力较大。

Von Mises当量应力分布如图6所示。从图中可见，榫接结构内的应力分布是极不均匀的，接触区域附近应力水平明显高于其它区域的，最大当量应力出现在榫槽第3齿底转接圆弧处。

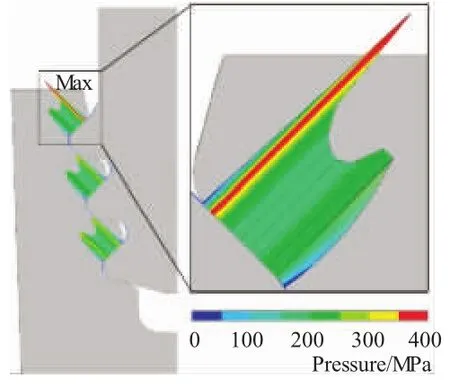
图5　初始设计接触压力分布

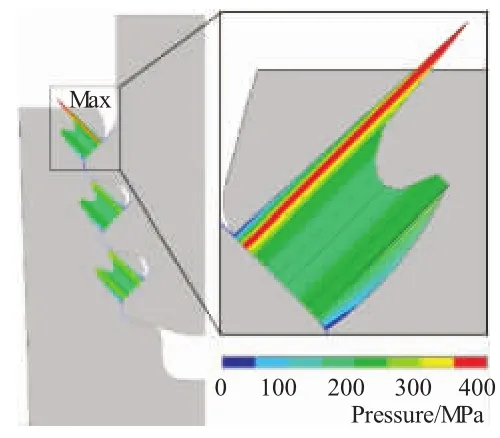
图6　初始设计当量应力

对榫槽各齿的应力情况进行进一步分析，提取榫槽各齿转接圆弧及接触区域的当量应力，如图7所示。从图中可见，无量纲长度在0～0.45内为转接圆弧，每对齿的最大当量应力均出现在这一区域，但其应力水平差别较大，第3齿的应力较其它齿高近25%；无量纲长度在0.45～1内包括了整个接触区域，在接触区域的中心应力水平较低，而边缘处出现了应力极值。

从上述分析可知，接触压力峰值出现在第1齿而当量应力峰值出现在第3齿，表明榫接结构各齿间的应力分布是不均匀的，如优化时3对齿仍采用一致的齿形参数，将不能获得较好的结果。因此，每对榫齿均采用相互独立的齿形参数，以提升优化空间。

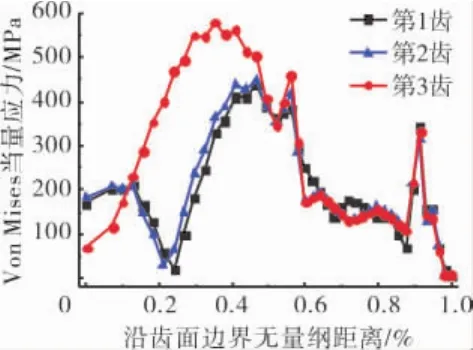
图7　初始设计中当量应力沿榫槽各齿边界分布

2　优化设计

2.1设计变量选取

若将每对榫齿的齿形参数都独立作为变量，虽然可以提高优化的潜力，但同时也带来设计变量过多的问题，需要近40个参数才能将该榫接结构的形状约束住，使得优化效率大大降低。因此采用试验设计的方法对参数进行筛选，提取影响较大的参数作为设计变量。

试验设计的主要内容是讨论如何合理地安排试验、获取数据，然后进行综合而科学的分析。相较单一变量改变法，该方法能够考虑各因素间的交互效应，因而能够更加准确地评价各因素的影响。本文基于Isight平台的优化拉丁方方法进行试验设计。

优化拉丁方试验设计方法采用正交性较好的初始解，综合考虑拉丁方矩阵的正交性和均匀性，保证设计点能够均匀地散布在整个设计空间，使仿真方案具有较好的典型性和代表性［16］。试验设计流程如图8所示。

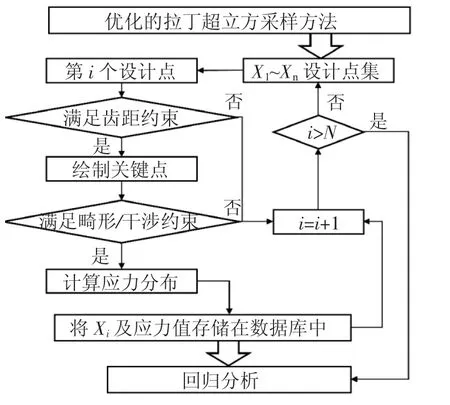
图8　试验设计流程

在分析过程中，为保证榫接结构形状合理，避免有限元方法无法收敛，需要对优化拉丁方方法给出的仿真点进行筛选。如前文所述，筛选分为齿距、畸形、干涉3部分。通过筛选，既保证了计算结果的可靠性，也提高了计算效率。

每一参数在初始设计±10%的范围内变化，得到结果后，进行线性回归分析，各参数对榫槽、榫头最大当量应力的影响因子如图9、10所示。

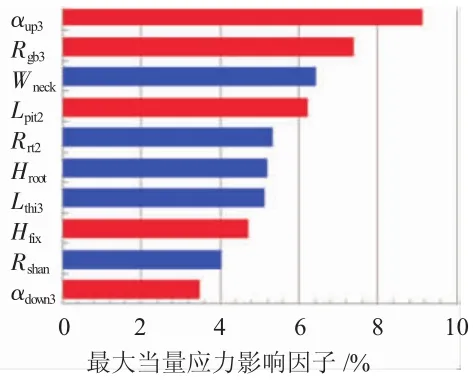
图9　几何参数对榫槽最大当量应力影响因子

图10　几何参数对榫头最大当量应力影响因子

图中红色为负效应，蓝色为正效应。表现为负效应的参数，随着参数的增大，结果有减小的趋势，负效应越大，其减小的趋势越明显；正效应则相反。

如前文所述，榫槽最大当量应力出现在第3齿底转接圆弧处。在这10项影响因子中，前4项均是涉及该处的参数，分别是：（1）第3齿上侧角。随其增大，会使接触长度增加，齿底变厚，榫槽第3齿的抗弯刚度增大。如将榫齿等效成悬臂梁进行定性分析［17］，齿底当量应力将减小，表现为负效应；（2）榫槽第3齿底转接圆弧半径。随其增大，应力过渡将更均匀，应力集中削弱，表现为负效应；（3）颈宽。随其增加，榫槽各截面长度减小，拉应力增大，表现为正效应；（4）第2齿距。随其增大，榫槽第3齿面积增大，抗弯刚度增大，表现为负效应。

对榫头而言，最大当量应力仍出现在第3齿的齿底转接圆弧处，影响最显著的前3项影响因子均与该处结构相关：（1）榫头高度。直接影响第3齿齿底厚度，增大榫头高度，齿底厚度增大，抗弯刚度增大，表现为负效应；（2）第3齿上侧角。表现为负效应，与榫槽第3齿一致；（3）定位线高度。与榫头高度相反，随其增大，在榫头高度不变的情况下，榫头第3齿底厚度将减小，表现为正效应。

除用于分析各参数的影响因子外，试验设计还可为下一步的优化设计提供初始参数。在试验设计的结果中选取1项改善设计，将其值赋予各结构参数，在此基础上，选取榫槽最大当量应力影响因子在5%以上的参数作为设计变量，在保证优化效果的同时提高优化效率。

2.2目标函数及优化流程

取目标函数为榫头、榫槽最大当量应力的加权值。

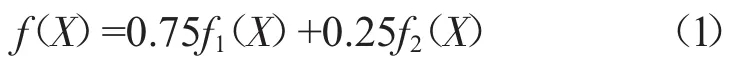
式中：f1（X）、f2（X）分别为榫槽、榫头最大当量应力。由于榫槽最大当量应力更大，因此其权重更大。

本文基于Isight平台的多岛遗传算法寻找优化结果，流程如图11所示。利用APDL条件语句在点线面逐步建模过程中提取各关键点坐标信息，判断是否符合几何约束。在每次ANSYS计算完成后，提取计算结果中的最大当量、接触、拉伸及弯曲应力值，其中当量应力作为目标函数，对于其它应力则判断是否超出许用应力，以作为性能约束。为保证遗传算法能够正常寻优，对不满足约束的设计点赋予较大的当量应力值，通过这种措施提高优化效率。

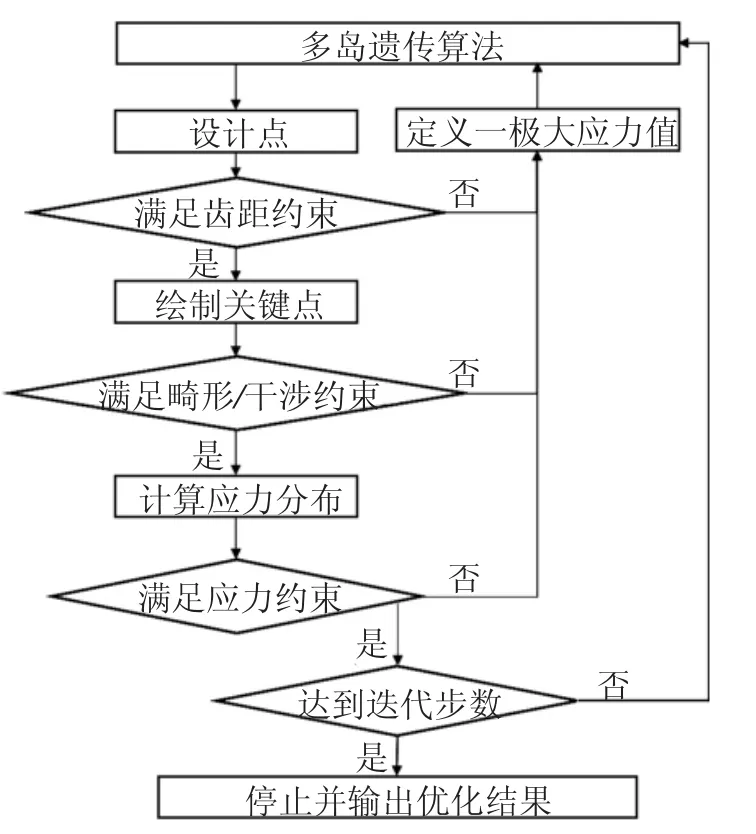
图11　基于多岛遗传算法的优化流程

3　结果分析

设计变量初始值与优化后值及结果对比见表3、4。从表中可见，榫槽最大当量应力降低了19.93%。

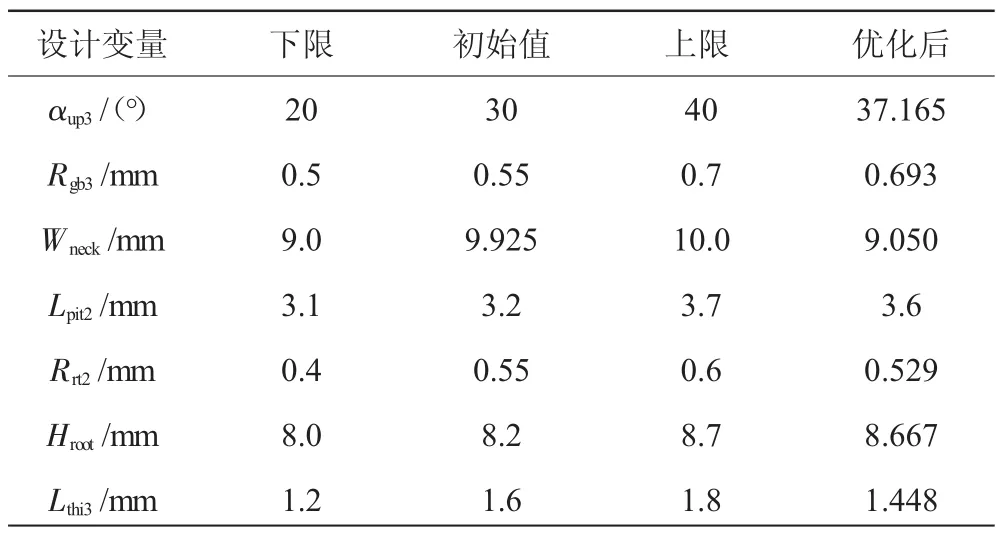
表3　设计变量优化结果

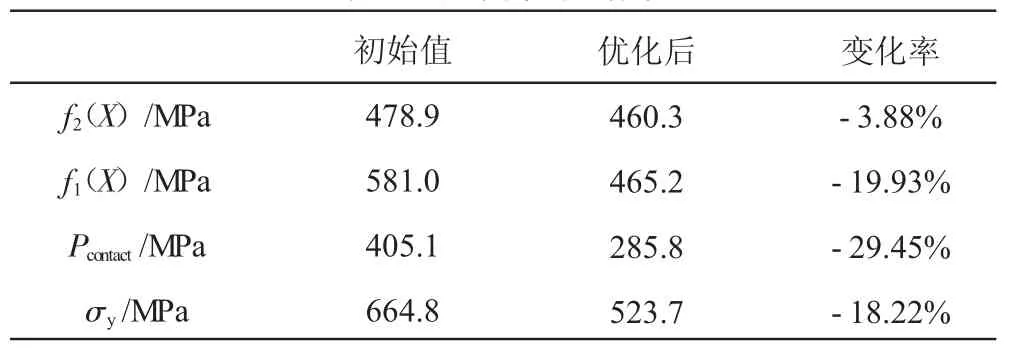
表4　应力优化结果

非设计变量采用试验设计结果中的改善设计，均有一定变化，榫接结构初始设计与优化设计形状对比如图12所示。

初始设计与优化后榫接结构当量应力对比如图13所示。从图中可见，与初始设计相比，最大当量应力由榫槽第3齿底转接圆弧处移至第1齿底转接圆弧处。

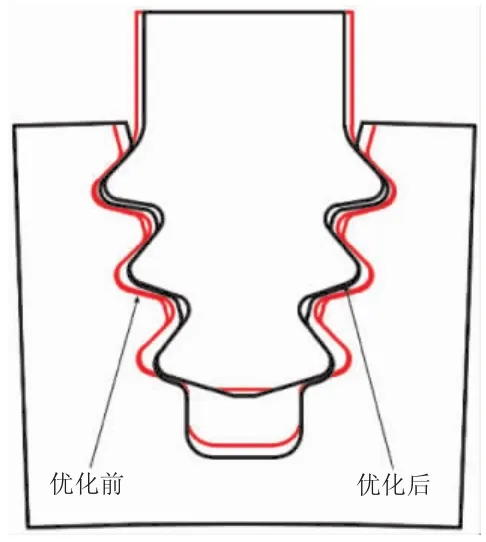
图12　优化前后榫接结构形状对比

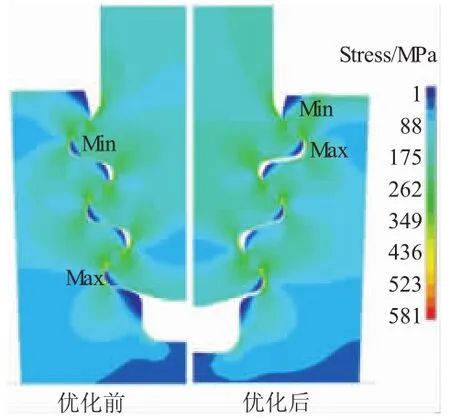
图13　优化前后榫接结构当量应力对比

优化前后榫槽第3齿的应力分布如图14所示。从图中可见，榫槽第3齿齿面的当量应力分布趋势未发生变化，但齿底转接圆弧处的应力集中状况得到明显改善。

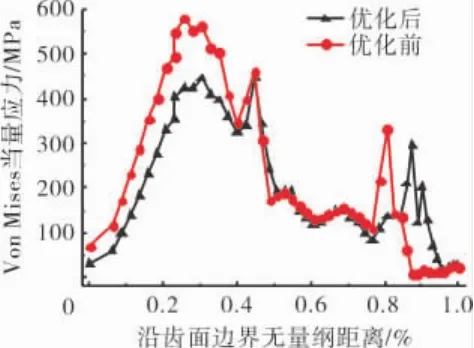
图14　优化前后当量应力沿榫槽第3齿分布对比

优化后榫槽各齿沿齿面的当量应力分布如图15所示。从图中可见，相较于初始设计，由于第3齿齿底转接圆弧处的应力峰值已经消失，各齿的受力状况变得一致。虽然最大当量应力移至第1齿齿底处，但各齿的应力水平一致，这将对榫接结构的寿命带来积极的影响。

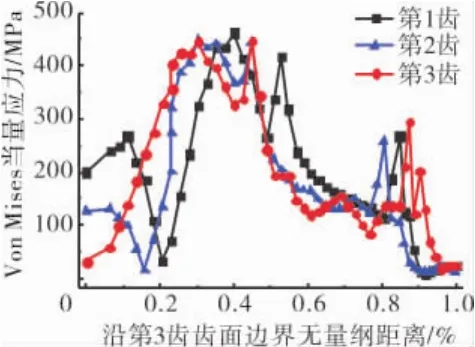
图15　优化后当量应力沿榫槽各齿边界分布

此外，榫头处的应力分布也变得更加均匀，优化前后榫头最窄截面处的拉应力分布情况如图16所示。从图中可见，虽然榫头中部的应力水平在优化后有所提高，但仍处于较低水平；同时，两侧的最大拉应力有所降低，榫头内部的拉应力分布变得更加均匀。

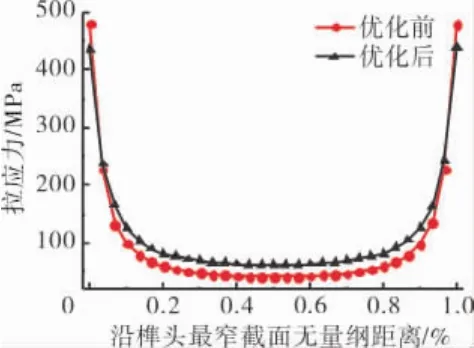
图16　优化前后拉应力沿榫头最窄截面分布对比

优化前后榫头第1齿接触压力分布情况如图17所示。从图中可见，接触压力在优化后峰值消失，分布更加均匀，最大弯曲应力由第3齿齿根移至第1齿齿根处。优化前后2处的弯曲应力分布如图18所示。从图中可见，弯曲应力极值在优化后减小，分布平缓。

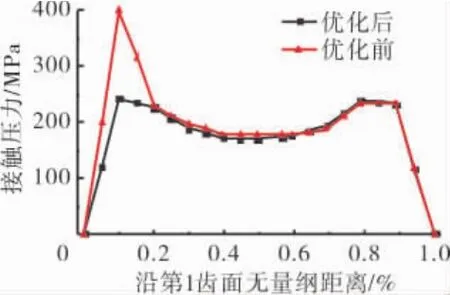
图17　优化前后接触压力沿第1齿面分布对比

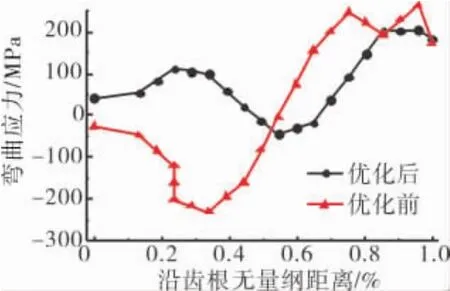
图18　优化前后最大弯曲应力沿齿根分布对比

综上，该榫接结构的各方面性能在优化之后都得到改善，也达到了优化设计的初衷。

4　结束语

本文分析了燃气轮机涡轮枞树形榫接结构应力情况，发现3对榫齿应力分布极不均匀，采用相同的齿形参数无法获得满意的优化结果。为此，对各榫齿采用不同的齿形参数进行参数化建模并优化。在优化之后，榫槽第3齿最大当量应力明显降低，各齿应力分布趋于一致，拉应力、接触压力及弯曲应力分布更加均匀，该设计方法确实能提升榫接结构的优化潜力，对其设计与优化具有一定参考价值。

［1］郑旭东，蔚夺魁，王兆丰，等.某型航空发动机涡轮叶片和轮盘榫齿裂纹故障力学分析［J］.航空发动机，2005，31（3）：35-38. ZHENG Xudong，YU Duokui，WANG Zhaofeng，etal.Mechanical analysis of crack failures in turbine blade and disk serration of an aeroengine［J］.Aeroengine，2005，31（3）：35-38.（in Chinese）

［2］Meguid S A，Kanth P S，Czekanski A.Finite element analysis of fir-tree region in turbine discs［J］.Finite Elements in Analysis andDesign，2000，35（4）：305-317.

［3］Song W，Keane A J，Rees J，et al.Local shape optimisation of turbine disc fir-tree using NURBS［C］//9th AIAA/SSMO Symposium on Multidisciplinary Analysis and Optimization.Atlanta：American Institute of Aeronautics and Astronautics，2002：1-11.

［4］Song W，Keane A J.An efficient evolutionary optimisation framework applied to turbine blade fir-tree root local profiles［J］.Structural and Multidisciplinary Optimization，2005，29（5）：382-390.

［5］Song W B，Keane A，Rees J，et al.Turbine blade fir-tree root design optimisation using intelligent CAD and finite element analysis［J］.Computers&Structures，2002，80（24）：1853-1867.

［6］赵海.涡轮榫头/榫槽结构设计方法研究［D］.南京：南京航空航天大学，2005. ZHAO Hai.Research on design method of turbine tenon/mortise［D］. Nanjing：Nanjing University of Aeronautics and Astronautics，2005.（in Chinese）

［7］申秀丽，齐晓东，王荣桥，等.航空发动机涡轮榫接结构齿形基本参数研究［J］.航空动力学报，2011，26（4）：735-744. SHEN Xiuli，QI Xiaodong，WANG Rongqiao，et al.Research on the dentiform basic parameters of aero-engine turbine joint structure［J］. Journal of Aerospace Power，2011，26（4）：735-744.（in Chinese）

［8］申秀丽，齐晓东，王荣桥，等.航空发动机枞树形榫头/榫槽结构形状优化［J］.工程力学，2011，28（12）：231-237. SHEN Xiuli，QI Xiaodong，WANG Rongqiao，et al.Shape optimization of aero engine fir-tree tenon/mortise structure［J］.Engineering Mechanics，2011，28（12）：231-237.（in Chinese）

［9］申秀丽，周莹舻.圆弧齿榫接结构应力的数值计算与分析［J］.航空动力学报，2012，27（3）：610-616. SHEN Xiuli，ZHOU Yinglu.Numerical calculation and analysis of arc tooth tenon joint［J］.Journal of Aerospace Power，2012，27（3）：610-616.（in Chinese）

［10］杨敏超，孙苏亚.涡轮榫头/榫槽的结构优化设计［J］.航空动力学报，2010，25（8）：1876-1882. YANGMinchao，SUNSuya.Structuraloptimizationofturbine tenon/mortise［J］.JournalofAerospacePower，2010，25（8）：1876-1882.（in Chinese）

［11］Zboinski G.Physical and geometrical nonlinearities in contact problems of elastic turbine blade attachments［J］.Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science，1995，209（4）：273-286.

［12］Sinclair G B，Cormier N G.Contact stresses in dovetail attachments：physical modeling［J］.Journal of Engineering for Gas Turbines and Power-Transactions of the ASME，2002，124（2）：325-331.

［13］Uchino K，Kamiyama T.Three-dimensional photoelastic analysis of aeroengine rotary parts［C］//Proceedings International Symposiumon Photoelasiticy.New York：Springer，1986：209-214.

［14］Sinclair G B，Cormier N G.Contact stresses in dovetail attachments：finite element modeling［J］.Journal of Engineering for Gas Turbines and Power-Transactions of the ASME，2002，124：182-189.

［15］Ali A A.Structural evaluation of a space shuttle main engine（SSME）high pressure turo pump turbine blade［R］.NASA-CR-1996-198428，.

［16］刘晓路，陈英武，荆显荣，等.优化拉丁方试验设计方法及其应用［J］.国防科技大学学报，2011，33（5）：73-77. LIU Xiaolu，CHEN Yingwu，JING Xianrong，et al.Optimized latin hypercube sampling method and its application［J］.Journal of National University of Defense Technology，2011，33（5）：73-77.（in Chinese）

［17］魏大盛，王延荣.榫连结构几何参数对接触应力的影响［J］.推进技术，2010，31（4）：473-477. WEI Dasheng，WANG Yanrong.Effects of geometrical parameters on distribution of contact stress in a tenon jointing［J］.Journal of Propulsion Technology，2010，31（4）：473-477.（in Chinese）

（编辑：栗枢）

Structural Analysis and Optimization of Gas Turbine Fir-Tree Attachment with Various Tooth Profile Parameters

ZONG Hong-ming1，2，TAO Hai-liang1，GAO Qing1，TAN Chun-qing1
（1.Institute of Engineering Thermophysics，Chinese Academy of Sciences，Beijing 100190，China；2.University of Chinese Academy of Sciences，Beijing 100049，China）

In the redesign of a gas turbine，stress concentration was seriously found in the three teeth fir-tree attachment，which may cause initiate crack.In order to decrease stress level and prolong service life，shape optimization was applied.Based on feature-based modelling method，2-D parametric model was established.When analyzing the original design，the same tooth profile parameters in design lacked improvement potential，so each tooth was modelled with various tooth profile parameters.The Optimized Latin Hypercube method was adopted to extract design variables from a large number of geometry parameters and the Multi-Island Genetic Algorithm was used to explore optimized design under constraints.The result indicates that the maximum Von Mises stress decreases by 19.93%and stress distribution becomes more uniform，various tooth profile parameters in design improves the optimization potential and provides a kind of reference to the design of fir-tree attachment.

a fir-tree attachment；contact stress；optimization design；turbine；gas turbine

V 231.91

A

10.13477/j.cnki.aeroengine.2016.04.013

2015-12-06基金项目：中国科学院基金（CXJJ-14-S119）资助

宗洪明（1991），男，在读硕士研究生，研究方向为燃气轮机结构强度分析与优化；E-mail：zonghongming@iet.cn。

引用格式：宗洪明，陶海亮，高庆，等.某型燃气轮机枞树形榫接结构多齿形参数优化分析［J］.航空发动机，2016，42（4）：64-69.ZONGHongming，TAO Hailiang，GAOQing，etal.Structuralanalysisandoptimizationofgasturbinefir-treeattachmentwithvarioustoothprofileparameters［J］.Aeroenging，2016，42（4）：64-69.