拉格朗日中值定理反问题存在性及存在不可导点的相关结论探讨
熊骏
(长江大学信息与数学学院,湖北 荆州 434023)
拉格朗日中值定理反问题存在性及存在不可导点的相关结论探讨
熊骏
(长江大学信息与数学学院,湖北 荆州 434023)
从几何意义出发研究拉格朗日中值定理的反问题,得到了拉格朗日中值定理反问题的2个存在性结论。此外,还探讨了函数有不可导点情形下拉格朗日中值定理的相关结论,丰富了拉格朗日中值定理的结果。
拉格朗日中值定理;反问题;不可导点
拉格朗日中值定理[1~5]是微分中值定理的核心,在数学分析的理论及应用中有很重要的作用。拉格朗日中值定理具体表述如下:
若函数f(x)在[a,b]上连续,在(a,b)内可导,则存在ξ∈(a,b),使得:
其几何意义是在曲线L:y=f(x)上存在点P(ξ,f(ξ)),曲线在该点的切线的斜率等于曲线上两点A(a,f(a)),B(b,f(b))确定直线AB的斜率。
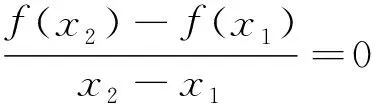
为此,笔者考虑增强函数f(x)的条件,使得上述拉格朗日中值定理反问题的存在性成立。另外,还考虑了若函数f(x)在[a,b]上连续,在(a,b)有不可导点的情形下拉格朗日中值定理的相关结论。
1 拉格朗日中值定理反问题的2个存在性结论
定理1设函数f(x)在[a,b]上二次可导,且f″(x)≠0(x∈[a,b]),则对任意的ξ∈(a,b),存在c∈[a,b],使得:
或
证明因f″(x)≠0(x∈[a,b]),由导数的介值定理可知,f″(x)(x∈[a,b])不可能变号,不妨设f″(x)>0(x∈[a,b]),于是f′(x)在[a,b]上严格单调递增。因此,对任意的ξ∈(a,b),有:
f′(a) 由定理1的证明中,二阶导数的作用可以适当减弱条件为f′(x)在[a,b]上严格单调,从而得到如下推论。 推论1设函数f′(x)在[a,b]上严格单调,则对∀ξ∈(a,b)存在c∈[a,b],使得; 或: 定理2设函数f(x)在[a,b]上二次可导,则对∀ξ∈(a,b),若f″(ξ)≠0,存在x1,x2∈(a,b),使得x1<ξ 证明不妨设f″(ξ)>0,由极限的局部保号性知,存在ξ的某邻域,在该邻域内f′(x)单调递增。即存在δ>0,当x∈(ξ-δ,ξ)时,f′(x) 分析f″(ξ)≠0在证明中的作用,由定理2可以得到如下推论。 推论2设函数f(x)在[a,b]上连续,在在(a,b)内可导,则对任意的ξ∈(a,b),若ξ不是f′(x)的极值点,则存在x1,x2∈(a,b),使得x1<ξ 证明不妨设a f(c1)-f(a)=f′(ξ1)(c1-a),ξ1∈(a,c1) f(c2)-f(c1)=f′(ξ2)(c2-c1),ξ1∈(c1,c2) ⋮ f(b)-f(cN)=f′(ξN+1)(b-cN),ξN+1∈(cN,b) 以上各式2边除以b-a再相加得到: 定理3中, N=1即为拉格朗日中值定理。 f(b)-f(c1)=f′(ξ1)(b-c1),ξ1∈(c1,b) f(c1)-f(c2)=f′(ξ2)(c1-c2),ξ1∈(c2,c1) ⋮ f(cn-1)-f(cn)=f′(ξn)(cn-1-cn),ξn∈(cn,cn-1) 以上各式两边除以b-a再相加,再取极限n→∞,得到: 拉格朗日中值定理的几何意义为思考某些问题提供了思路,加强函数的条件可以得到一些拉格朗日中值定理反问题的存在性结果。在今后的研究中,还可以通过加强函数的条件考虑拉格朗日中值定理中点的存在个数问题。 [1]华东师范大学数学系.数学分析(上册) [M]. 第3版.北京:高等教育出版社,2005. [2]刘三阳,于力,李广民.数学分析选讲[M].北京:科学出版社,2006. [3]同济大学数学系.高等数学(上册)[M]. 第6版.北京:高等教育出版社,2006. [4]四川大学数学系.高等数学(第一册)[M]. 第2版.北京:高等教育出版社,1989. [5]冉兆平.微积分[M]. 第2版.上海:上海财经大学出版社,2008. [编辑]张涛 2016-04-20 熊骏(1967-),男,硕士,副教授,现主要从事基础数学方面的教学与研究工作;E-mail:cjdxxj@163.com。 O172.1 A 1673-1409(2016)22-0060-04 [引著格式]熊骏.拉格朗日中值定理反问题存在性及存在不可导点的相关结论探讨[J].长江大学学报(自科版),2016,13(22):60~63.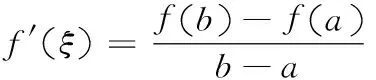
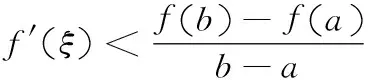
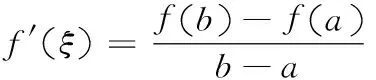
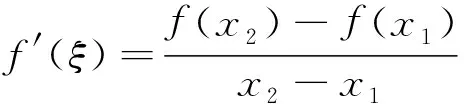
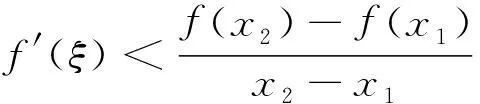
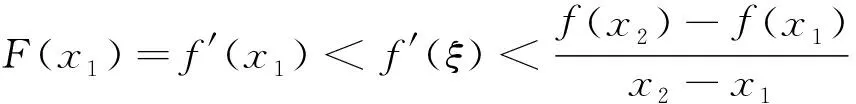
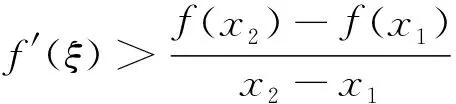
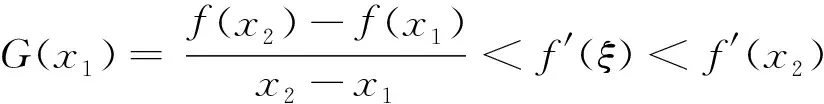
2 存在不可导点情形下拉格朗日中值定理的相关结论
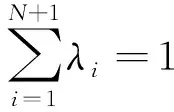
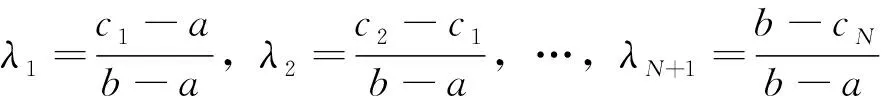
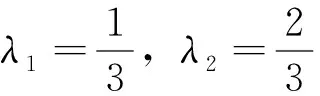
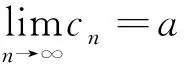
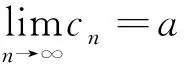
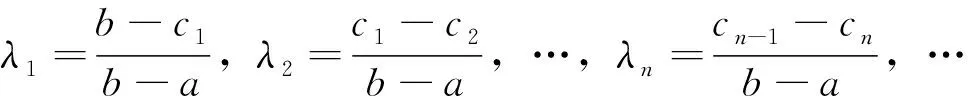
3 结语

