基于方向导数的多元函数极值的判定

马烁

(荆州理工职业学院基础课部， 湖北 荆州 434000)

梁向

(荆州市沙市第一中学， 湖北 荆州 434000)



基于方向导数的多元函数极值的判定

马烁

(荆州理工职业学院基础课部， 湖北 荆州 434000)

梁向

(荆州市沙市第一中学， 湖北 荆州 434000)

首先给出一阶方向导数和二阶方向导数的定义及其与偏导数的关系，然后利用方向导数给出了判断二元函数在驻点或偏导数不存在的点处是否取得极值的2个充分条件。实例分析结果表明，利用方向导数来判断驻点或不可导是否为极值点是有效的。

方向导数；二元函数；极值；判别法

函数的极值不仅是函数性态的重要特征，而且在实际中有广泛应用。一般的教材[1,2]上都是利用二阶连续偏导数来判断驻点是否为多元数的极值，但是对于多元函数的不可导点，这一方法就失效了。文献[3～8]利用高阶偏导数或实二次型的理论求解多元函数的极值，但比较繁琐。下面，笔者利用方向导数给出判断多元函数的驻点或不可导点处是否为极值的条件及求法。

1　方向导数及其与偏导数的关系

定义1[1]设函数z=f(x,y)在点P(x0,y0)的某个邻域内有定义，l是从P(x0,y0)出发沿方向el=(cosα,cosβ)的一条射线,在l上任取一点P(x,y)，有x=x0+tcosα，y=y0+tcosβ(t≥0),如果极限：

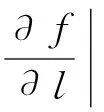
定理1[2]如果函数z=f(x,y)在点P(x,y)可微分,那么函数在该点沿任一方向l(cosα,cosβ)的方向导数都存在,且有：

(1)

式(1)表示为(x,y)的一个函数，称为方向导函数，简称方向导数。

对于方向导函数式(1)，可以求关于方向l(cosα,cosβ)的方向导数。

定义2设函数z=f(x,y)在点P(x,y)的某个邻域内沿l(cosα,cosβ)的方向导数存在，对于l(cosα,cosβ)，如果极限：

存在，则称该极限为函数z=f(x,y)在点P(x,y)沿l(cosα,cosβ)的二阶方向导数。

定理2如果函数z=f(x,y)在点P(x,y)二阶可微，则在点P(x,y)沿方向l(cosα,cosβ)的二阶方向导数存在，且有：

定理2由二阶方向导数的定义可以证明。

2　多元函数极值的判定方法

二元函数的极值可能在驻点处取得，也可能在偏导数不存在的点处取得，下面给出利用方向导数判断二元函数在驻点或偏导数不存在的点处是否取得极值的判别方法。

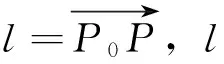
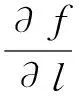
同理可证(2)、(3)。

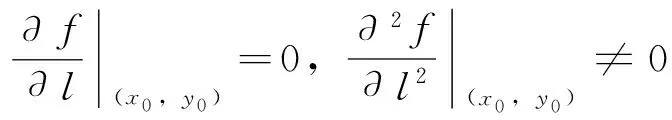
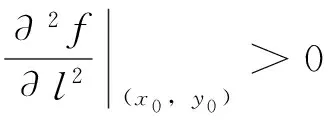
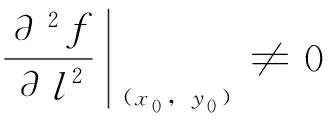
3　实例分析

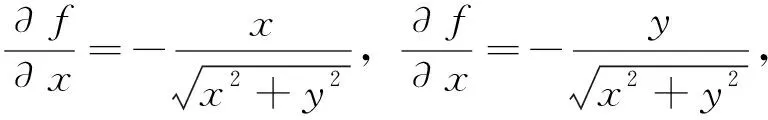
则：

例2讨论函数f(x,y)=x2-y2在点(0，0)处的极值情况。

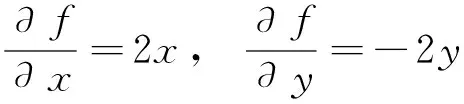
则：

f(x,y)=x2-y2在点O(0,0)的去心邻域内方向导数既有大于零的又有小于零的，符号不确定，于是由定理3知函数f(x,y)=x2-y2在O(0,0)处不取极值。

例3讨论函数f(x,y)=x3+y3-3xy在点(1,1)处的极值情况。

解由于：

=6xcos2α-3cosαcosβ-3cosβcosα+6ycos2β

所以对于任意方向l(cosα,cosβ)，有：

故由定理4知函数f(x,y)在(1,1)处取得极小值。

4　结语

利用方向导数给出了判断二元函数在驻点或偏导数不存在的点处是否取得极值的2个充分条件。通过实例分析，结果表明利用方向导数来判断驻点或不可导是否为极值点是有效的。 这种判别方法可以推广到三元及三元以上的函数。

[1]同济大学应用数学系.高等数学(下册)[M].第5版，北京：高等教出版社，2002:52～55.

[2] 王安平，杨波，周云才.高等数学(下册)[M].长沙：湖南教育出版社，2013:89～92.

[3] 叶淼林.关于多元函数的极值[J].安庆师范学院学报(自然科学版),1995,1(4)：71～73.

[4] 吴崇剑，李伟.二元函数极值的高阶判别法[J]. 工科数学,1995,1(11)：104～107.

[5] 李玲.关于多元函数极值问题的讨论[J].重庆职业技术学院学报,2006,15(2)：163～165.

[6] 董丽华.实用二次型理论解多元函数的极值问题[J].淮北煤炭师范学院学报,2006,27(2)：28～30.

[7] 王敏芝.关于多元函数的极值的判别准则[J].浙江理工大学学报,2007,24(5)：592～596.

[8] 朱用文，王燕，候汝臣.正定矩阵在函数极值中的应用[J].数学的实践与认识,2010,40(21)：249～250.

[编辑]洪云飞

2016-04-25

湖北省教育科学“十二五”规划2012年度立项课题(2012B310)。

马烁(1981-),女，硕士，讲师，现主要从事最优化理论与算法方面的教学与研究工作；E-mail:mashuo050@163.com。

O171.2

A

1673-1409(2016)22-0064-04

[引著格式]马烁,梁向.基于方向导数的多元函数极值的判定[J].长江大学学报(自科版)，2016,13(22)：64～67.