基于遗传思想的改进粒子群优化算法

佘晓鑫，许波

(广东石油化工学院计算机与电子信息学院，广东 茂名 525000)



基于遗传思想的改进粒子群优化算法

佘晓鑫，许波

(广东石油化工学院计算机与电子信息学院，广东 茂名 525000)

传统的粒子群优化算法(Particle Swarm Optimization, PSO)在解决有关离散优化的问题时，容易发生早熟收敛，陷入局部最优等现象，从而得不到最优解。为了克服这种现象，提出了一种基于遗传思想的改进PSO算法：利用繁殖法更好的搜索粒子的空间，经过繁殖后的粒子可以更好的从局部最优逃离,并对经典的测试函数进行了测试。测试结果表明, 与传统的PSO算法相比, 改进算法的寻优效果较好，不仅能加快收敛速度，而且能找到同样甚至更好的解。

粒子群算法；局部最优；群体智能；算法设计；遗传算法；

粒子群算法(Particle Swarm Optimization, PSO)由美国电气工程师Eberhart和社会心理学家Kennedy于1995年正式提出[1]，其源于对鸟群捕食行为的研究，模拟鸟群飞行觅食的行为，通过鸟之间的集体协作使群体找到最优[2]。假设一群鸟在一个空间里随机地寻找食物，并且在这个空间里只有一份食物，同时所有的鸟都不知道食物在哪里，但是它们能判断自己的位置距离要找的食物还有多远。如果要找到食物的话，最简单有效的方法就是搜索食物的附近的鸟，然后查找鸟的周围的区域，利用在搜索的时候鸟的经验和自身的经验就可以很快的找出食物在哪里了。PSO 算法就从这种生物种群行为特性中得到启发并用于求解优化问题[3]。如果将鸟的这种捕食行为与粒子群优化搜索最优解的方法相对应, 那么每个问题的解对应着搜索空间中的一只鸟，将这只鸟想象为一个只有位置和速度的“粒子”,每个粒子的适应值由一个给定的函数计算得出，粒子的飞行方向和飞行的距离由一个速度量决定。假设粒子知道它到目前为止发现的最好的位置即最优解的位置[4]。不仅如此，每一个粒子自己知道到目前为止，所搜索过的群体中最好的位置在哪里。由此看来求解最优解的过程就可以看成鸟类协作寻找食物的过程，最优解的位置就是食物的位置。

PSO算法具有算法简洁，易于实现，需要调整的参数少，而且不需要梯度信息等优点，是解决非线性连续优化问题、组合优化问题和混合整数非线性优化问题的有效工具[5,6]。但该算法的全局搜索能力弱，经常发生早熟收敛的现象，容易陷入局部最优从而得不到最优解的情况。为此，笔者提出了一种基于遗传思想的改进PSO算法。

1　基本粒子群算法

在粒子群算法中，每个个体称为一个“粒子”同时对应着一个潜在的解[7]。PSO初始的时候随机产生一群粒子(随机解)，通过迭代的方式利用2个最优解来更新自己，一个是粒子个体到目前为止找到的局部最优解pbest，另一个是整个粒子群体到目前找到的全局最优解gbest。根据这2个最优解，粒子用式(1)和式(2)来更新自己的飞行速度和位置：

(1)

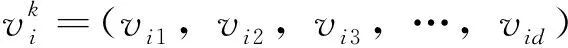
基本PSO算法的流程[8,9]如下：

1) 初始化。一开始设定粒子的各类参数：搜索范围，种群规模，学习因子，算法的最大迭代数还有收敛度，粒子速度的范围。从个体极值中找出最优的作为全局极值，并记录下来。

2) 检测粒子适应值。通过所给函数可以计算得出粒子的适应值，当结果比目前粒子本身经历过的最优值pbest还要好，则更新pbest。比目前粒子群经历的位置还好时更新gbest。

3) 迭代寻优。通过式(1)和式(2)对粒子的速度和位置进行更新。

4) 检验结果。如果当前迭代次数达到了预设定的最大次数或群体迄今为止搜索到的最优位置满足预定的最小的适应阈值，则停止迭代，得出最优解。否则执行步骤2。

基本的PSO算法在单峰函数中较容易找到极值，因为其函数就只有一个解，所以找到的这个局部极值可以认为是全局最优解，但是多峰函数不同，局部的极值不一定是全局最优解，算法容易把局部最优解当作全局最优解得出结论，从而得不到所需要的最优解[10]。

2　算法改进思想

在基本粒子群算法的粒子速度公式基础上，增加惯性权值w，位置更新公式不变。当w 较大时全局搜索能力强，局部搜索能力弱，有利于开拓；当w 较小时候全局搜索能力弱，局部搜索能力强，有利于收敛。所以一般把w的值设置为一个随时间减少的函数。根据改进速度更新公式计算新粒子的速度：

(3)

(4)

式中，wmax、wmin分别为最大、最小惯性权值；nk表示此时的迭代次数；nmax为当前最大的迭代次数。

但是在解决一些问题的时候，改进算法还是不能有效的得出最优解，如多峰函数求解最优值的问题，因为多峰函数有多个局部最优值的“误导”,使得函数还没有找到最优解就陷入了局部最优中，即把局部最优解当成全局最优解来看待了，造成了算法的停滞。故笔者在上述改进的基础上再做如下的改进，即当目前粒子的解等于粒子个体历史所搜寻到的最优解pbest，或当粒子目前寻找到的解等于粒子群经历过的历史最优解gbest时，可以认为算法出现了上述的停滞状态，这时将这个粒子与处于历史局部最优的粒子进行杂交，利用式(5)、(6)和式(7)、(8)对粒子的位置和速度进行更新：

child1(xi)=piparent1(xi)+(1-pi)parent2(xi)

(5)

child2(xi)=piparent2(xi)+(1-pi)parent1(xi)

(6)

(7)

(8)

式中，pi是[0,1]之间的随机数(经验值为0.2)。

这种方法可以很好的搜索到整个粒子群的空间，快速的搜索到所有的解，当粒子陷入了局部最优时，容易跌入快速下降的陷阱，但经过迭代繁殖后粒子很容易脱离局部最优的束缚，同时产生同样数目的子代，粒子的种群数目不变，保证了种群多样性，这种方法的好处在于可以使粒子脱离局部最优的约束，避免了算法的停滞，加快收敛速度，而且找到了同样甚至更好的解。

具体实现思路如下:计算粒子的适应度时，如果当前粒子的适应度等于历史个体粒子的最优解pbest，或者当前粒子的适应度等于历史全局最优解gbest时，将这个粒子与处于历史局部最优的粒子进行杂交，利用式(5)、(6)和式(7)、(8)对粒子的位置和速度进行更新。如果粒子的个体极值pbest优于全局极值gbest，则将个体极值取代原来的全局极值，即更新gbest。

3　算法步骤

1)初始化。设定粒子的各类参数：搜索范围，种群规模，惯性权值w的上下限，学习因子，算法的最大迭代数还有收敛度，粒子速度的范围。从个体极值中找出最优的作为全局极值，并记录下来。

2)按照所给函数计算粒子的适应值。

3)按照式(4)计算惯性权值w的值。

4)根据原公式对粒子更新位置，并对粒子进行位置限幅处理。

5)根据所给函数重新评价各粒子的适应值。

6)计算粒子的适应度，如果当前粒子的适应度等于粒子个体历史所搜寻到的的最优解pbest，或者当前粒子的适应度等于粒子群经历过的历史最优解gbest时，将这个粒子与处于历史局部最优的粒子进行杂交，利用式(5)、(6)和式(7)、(8)对粒子的位置和速度进行更新。

7)如果粒子的个体极值优于全局极值，则将个体极值取代原来的全局极值成为新的全局极值。

8)检验是否满足结束的条件。如果当前迭代次数达到了预设定的最大次数或群体迄今为止搜索到的最优位置满足预定的最小的适应阈值，则停止迭代，输出最优解。否则返回步骤2)。

4　测试结果与分析

采用Matlab工具实现PSO算法，通过对基本粒子群算法和改进粒子群算法的函数测试曲线分析得出结论，采用函数为基本测试函数。

测试函数1(Ackley函数)：

这是一个无约束优化问题，函数为连续、旋转、不可分离的多峰函数。主要通过一个余弦波形来调整指数函数,该函数特征是由余弦波调制而成的“峰”，使得该函数变得起伏不平。其全局最优解在边缘上，如果算法的初始值在边缘上，那么很快就可以解决问题，但在这里的形式更加普遍，维数可调整。其拓扑结构特征是：函数的周围边缘的部分平坦，在中间出现一个突出来的峰值，从而函数的图形变得起伏不平。该多峰函数具有大量的局部最优点。测试结果如图1所示。

图1　Ackley函数测试结果

测试函数2(Rastrigin 函数)：

这个函数基于Sphere函数的基础，运用了余弦函数产生了许多局部最优解，是一个比较复杂的多峰函数处理问题，该函数很容易陷入局部最优解，将局部最优作为最终结果，从而得不到全局最优解，全局最优解f(x)=0在点x=(0,…,0)处。测试结果如图2所示。

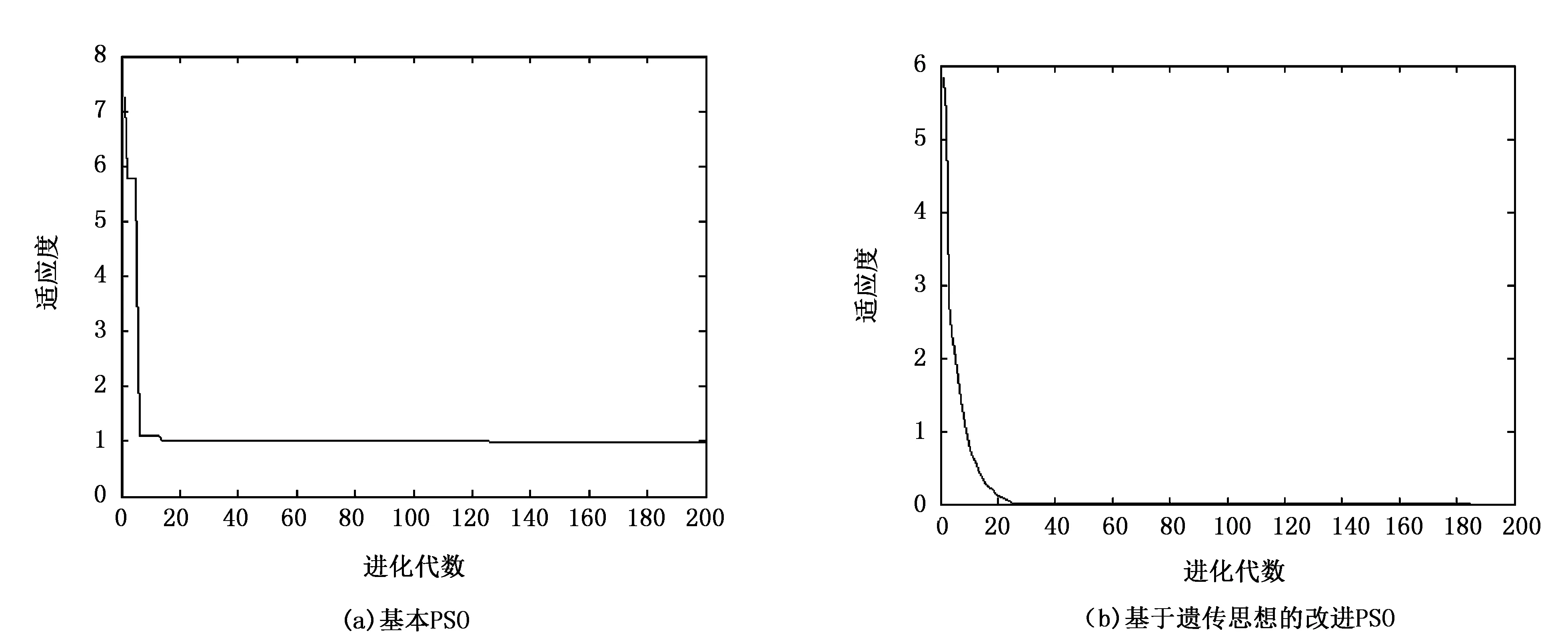
图2　Sphere函数测试结果

测试函数3(Shaffer函数):

该函数是一个多峰函数，有无数个极小值点，一般很难找到全局最优解，其中只有一个最小值的点，就是当函数在(0，0)的时候，函数有最小值为0。测试结果如图3所示。

图3　Shaffer函数测试结果

从测试结果图1～图3来看，基本粒子群算法在解决多峰函数的问题的时候容易陷入局部最优值，跌入快速下降的陷阱，得到的全局最优解往往偏差较大，而改进的粒子群算法在陷入局部最优的时候能较好的跳出局部最优解，继续寻找，避免了算法停滞，最终得到的解往往比基本粒子群算法更好。

5　结语

提出了一种基于遗传思想的改进PSO算法，并对经典的测试函数进行了测试，试验结果表明，与传统的PSO算法相比，改进的算法的寻优效果较好，不仅能加快收敛速度，而且能找到同样甚至更好的解。

[1]纪震，廖惠连，吴青华. 粒子群算法及应用[M] .北京：科学出版社，2009：58～64.

[2]Xu Bo, Guan Qing , Chen Ke. Multi-agent Coalition Formation Based on Quantum-behaved Particle Swarm Optimization [J].Journal of Information and Computational Science, 2010,7(5):1059～1064.

[3]温涛, 盛国军, 郭权, 等. 基于改进粒子群算法的 Web 服务组合[J]. 计算机学报, 2013, 36(5): 1031～1046.

[4]范成礼, 邢清华, 范海雄, 等. 带审敛因子的变邻域粒子群算法[J]. 控制与决策, 2014, 29(4): 696～700.

[5]Mandal D, Kar R, Ghoshal S P. Digital FIR filter design using fitness based hybrid adaptive differential evolution with particle swarm optimization [J]. Natural Computing, 2014, 13(1): 55～64.

[6]Palafox L, Noman N, Iba H. Reverse engineering of gene regulatory networks using dissipative particle swarm optimization [J]. Evolutionary Computation, IEEE Transactions on, 2013, 17(4): 577～587.

[7]周新宇, 吴志健, 王晖, 等. 一种精英反向学习的粒子群优化算法[J]. 电子学报, 2013, 41(8): 1647～1652.

[8]温雅, 李国, 徐晨. 一种带交叉因子的双向寻优粒子群优化算法[J]. 计算机应用研究, 2013, 30(1): 82～85.

[9]朱兆杰, 贾振红, 覃锡忠,等. 基于改进的粒子群算法的移动互联网扩散预测[J]. 计算机应用与软件, 2015, 32(7):126～128.

[10]Xu Bo, Yang Zhaofeng, Ge Yu, et al. Coalition formation in multi-agent systems based on improved particle swarm optimization algorithm [J]. International Journal of Hybrid Information Technology，2015, 8(3)：1～8.

[编辑]洪云飞

2016-04-27

国家自然科学基金项目 (61272382), 广东省云机器人(石油化工)工程技术研究中心项目 ( 2015B090903084)；广东省教育厅青年创新人才类项目(自然科学类)(2015KQNCX099)。

许波(1982-), 男, 博士，副教授，现主要从事计算智能方面的教学与研究工作；E-mail:xubo807127940@163.com 。

TP18

A

1673-1409(2016)22-0004-05

[引著格式]佘晓鑫，许波.基于遗传思想的改进粒子群优化算法[J].长江大学学报(自科版)，2016,13(22)：4～8.