应变能最小的保正有理三次样条插值曲线
赵前进, 张澜
(安徽理工大学理学院,安徽 淮南 232001)
应变能最小的保正有理三次样条插值曲线
赵前进, 张澜
(安徽理工大学理学院,安徽 淮南 232001)
构造了一种有理三次样条插值函数,该插值函数含有参数,具有较好的可约束性,并简述了插值曲线保正的充要条件和插值曲线的应变能。为构造应变能最小的保正有理三次样条插值曲线,以形状参数和节点处的导数为决策变量,以插值曲线应变能最小为目标函数,以形状参数大于零以及插值函数保正为约束条件,建立了一个优化模型,求解获得应变能最小的保正有理三次样条插值曲线。数值例子验证了该方法的可行性。
有理三次样条插值;保正;应变能;最优化
利用有理样条进行保正插值是几何造型领域中的研究热点之一 。文献[5]介绍的保正有理样条插值函数中的形状参数和节点处导数的选取过程主要根据插值函数保正的约束条件不断地尝试选取适当的形状参数,计算量过大。在此基础上为了构造应变能最小的保正有理三次样条插值曲线,笔者给出插值算法是以形状参数和节点处的导数为决策变量,以插值曲线应变能最小为目标函数,以形状参数大于零以及插值函数保正作为约束条件,建立优化模型,求解获得应变能最小的保正有理三次样条插值曲线。
1 插值函数的构造
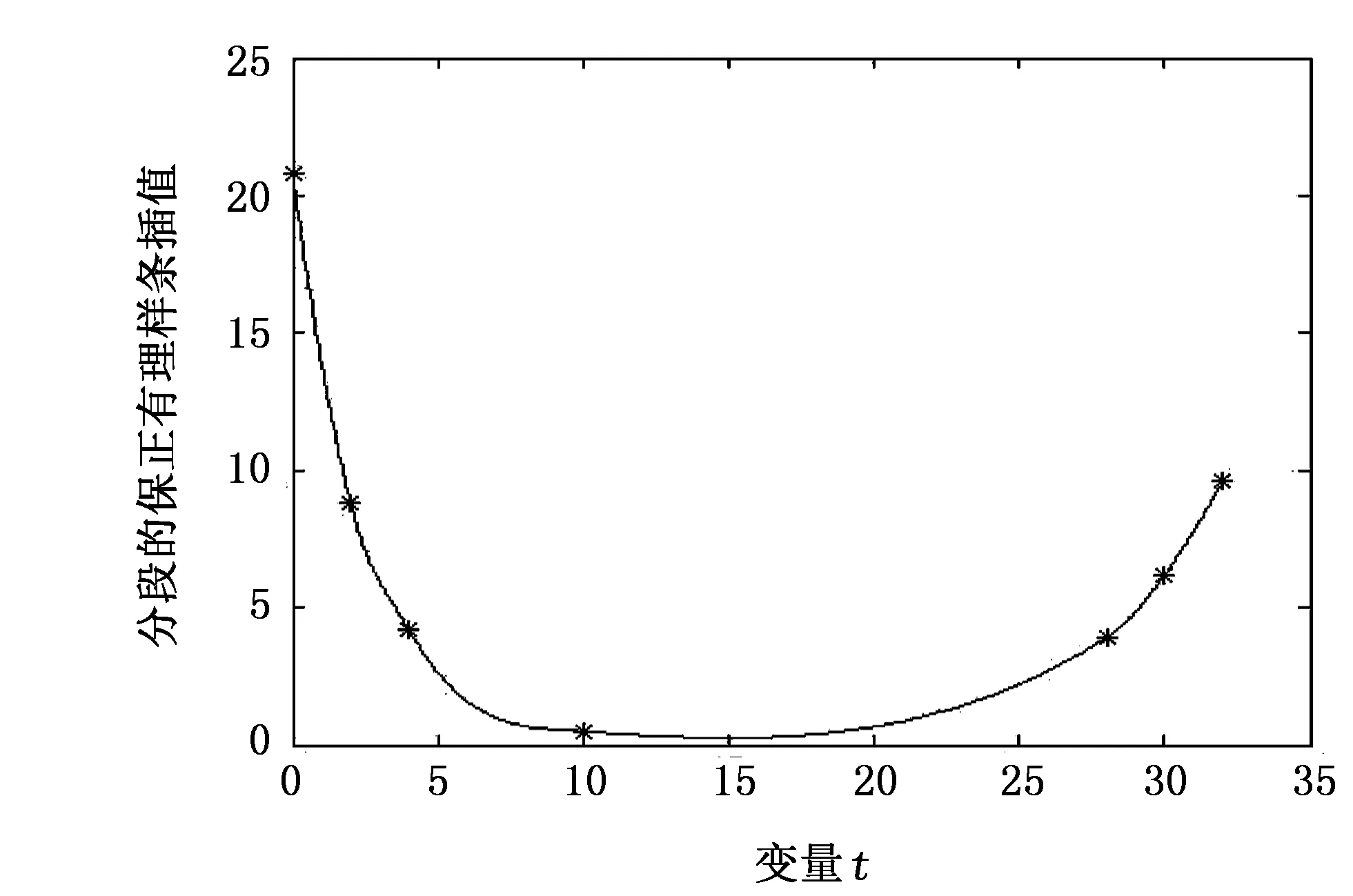
给定的一组数据{(ti,fi),i=0,1,…,n},对区间[a,b]进行划分:a=t0 (1) pi(t)=αifi(1-θ)3+ui(1-θ)2θ+vi(1-θ)θ2+βifi+1θ3qi(t)=αi(1-θ)+βiθ (2) ui=(2αi+βi)fi+αihidivi=(αi+2βi)fi+1-βihidi+1 (3) 式中, αi和βi被称为形状参数,αi>0,βi>0;di是插值函数P(t)在节点ti处的导数值。 由式(2)和式(3)易知,有理样条插值P(t)满足下列插值性质: P(ti)=fii=0,1,…,n (4) 取一组正数据{(ti,fi),i=0,1,…,n},其中: t0 (5) 由于已经假设形状控制参数αi>0,βi>0,故分母qi(t)在t∈[ti,ti+1]上恒大于零,再分析分子pi(t),由于pi(t)>0的充要条件为αi>0,βi>0,ui>0,vi>0,从而得出P(t)在区间[ti,ti+1]上的保正充要条件为: (6) 定理1给出一组满足式(4)的正数据,有理三次样条插值函数表达式(1)中的参数αi、βi和节点处的导数di满足条件(6),即可得到保正的插值曲线。 插值曲线P(t)在区间[t0,tn]上C2—连续曲线的应变能[8~10]定义如下: (7) 积分化简得: (8) 其中: 为构造应变能最小的保正有理三次样条插值曲线,以形状控制参数αi、 βi和节点处的导数值di为决策变量,以插值曲线应变能最小为目标函数,以形状参数大于零以及插值函数保正为约束条件,建立优化模型: (9) 求解此优化模型得最优参数αi、 βi和di,从而得到应变能最小的保正有理三次样条插值线。 由文献[11]可知,保正有理三次样条插值函数的误差有以下结论。 定理2设f(t)∈C1[a,b],P(t)是f(t)如式(1)所定义的分母为线性的有理样条插值,对给定的αi、βi,当t∈[ti,ti+1],i=0,1,…,n-1时有: |R[f]|=‖f′(t)-P(t)‖≤‖f′(t)‖hicii=0,1,…,n 其中: 定理3对任意αi>0,βi>0,定理2中的误差参数ci是有界的,且: 给出一组单调递增的数据:t0=0,t1=2,t2=4,t3=10,t4=28,t5=30,t6=32,f(t0)=20.8,f(t1)=8.8,f(t2)=4.2,f(t3)=0.5,f(t4)=3.9,f(t5)=6.2,f(t6)=9.6。由上述方法建立模型求解得表1所示结果。 图1 数值例子的插值曲线 保正有理三次样条插值曲线图形如图1所示。 表1 参数αi,βi和di 的值 笔者构造的分母为线性的有理三次样条插值函数,因表达式中具有参数,给控制插值曲线的形状带来了方便。为确定参数的值,笔者给出的求解形状控制参数和节点处的导数值的方法比以往的算法改进很多。计算速度有所提高,计算过程精简很多,通过建立优化模型求解应变能最小时保正的有理三次样条插值曲线。但也存在一些不足,该方法具有局限性,只能用于分母为线性的有理三次样条插值函数,其分母为二次或三次函数的有理三次插值样条插值函数以及有理四次样条插值函数还有待下一步研究。 [1]Hussain M Z, Sarfraz M. Positivity-preserving interpolation of positive data by rational cubics[J]. Journal of Computational & Applied Mathematics, 2008, 218(2):446~458. [2] Schmidt J W, Heβ W. Positive interpolation with rational quadratic splines[J]. Computing, 1987, 38(3):261~267. [3] Schmidt J W, Heβ W. Positivity of cubic polynomials on intervals and positive spline interpolation[J]. BIT Numerical Mathematics, 1988, 28(2):340~352. [4] 田萌. 一类保正的有理三次插值样条[J]. 山东理工大学学报:自然科学版, 2006, 20(3):16~18. [5] Sarfraz M. Visualization of positive and convex data by a rational cubic spline interpolation[J]. Information Sciences, 2002, 146(1-4):239~254. [6] Sarfraz M, Hussain M Z, Shaikh T S. Visualization of Positive Data by Rational Cubic Spline Interpolant[J].Internation Conference on Information Visualisation,2010, 132(11):564~569. [7] 段奇, 刘爱奎, 曹建胜,等. 一种三次约束有理插值样条及其逼近性质[J]. 中国石油大学学报:自然科学版, 2001, 25(6):95~98. [8] Duan Q, Bao F, Du S, et al. Local control of interpolating rational cubic spline curves[J].Computer-Aided Design, 2009, 41(11):825~829. [9 ]Zhang C, Zhang P, Cheng F. Fairing spline curves and surfaces by minimizing energy[J]. Computer-Aided Design, 2001, 33(13):913~923. [10] Bao F, Sun Q, Pan J, et al. A blending interpolator with value control and minimal strain energy[J]. Computers & Graphics, 2010, 34(2):119~124. [11] Tian M, Geng H. Error analysis of a rational interpolation spline[J]. International Journal of Mathematical Analysis, 2011, 5(25):1287~1294. [编辑]洪云飞 2016-04-19 国家自然科学基金项目(60973050 );安徽省教育厅自然科学基金项目(KJ2009A50)。 赵前进(1967-),男,博士,教授,现主要从事有理插值与逼近、数字图像处理方面的教学与研究工作;通信作者:张澜,15137696003@163.com。 O241.3 A 1673-1409(2016)22-0001-03 [引著格式]赵前进, 张澜.应变能最小的保正有理三次样条插值曲线[J].长江大学学报(自科版),2016,13(22):1~3.2 保正分析
3 优化模型的建立
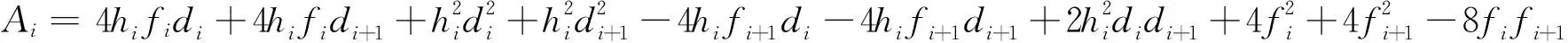
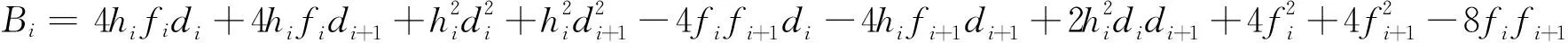
4 数值分析

5 结语

