教学《优化——烙饼》的分歧

谢洪明　李晓燕

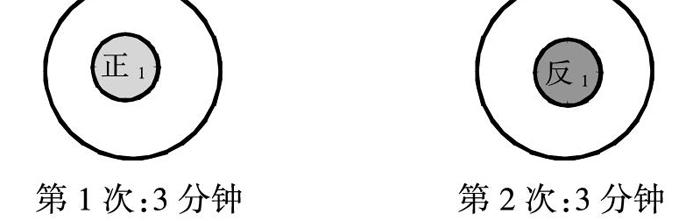
笔者在教学《优化——烙饼》（小学四年级上册数学），与教研员产生了分歧，笔者个人观点陈述如下，供大家商榷和指正。相关内容具体情况如下：

一、课程主要环节

1.烙1张饼（分析推理—实践操作—画图记录）

每张饼2面，每次烙1个面3分钟，烙2个面就是2个3分钟，一共6分钟，操作和画图印证，图示如下：

第1次：3分钟 第2次：3分钟

2.烙2张饼（分析推理—实践操作—画图记录）

（1）猜测与操作：猜测2张饼烙4次12分钟（轮流），2张饼子同时烙2次6分钟（时间最少）

（2）比较与说明：烙饼1张和2张时间都是6分钟，同时烙2张饼（锅没闲）节省时间。

（3）推理与证明： 2张饼同时烙2次（2个3分钟）是6分钟，

（4）发现规律：同时烙饼，2张饼一共4面，每次烙2面，要烙2次，次数等于张数；“1张饼烙1次（1个3分钟）最少3分钟”（归一法推理得出）；

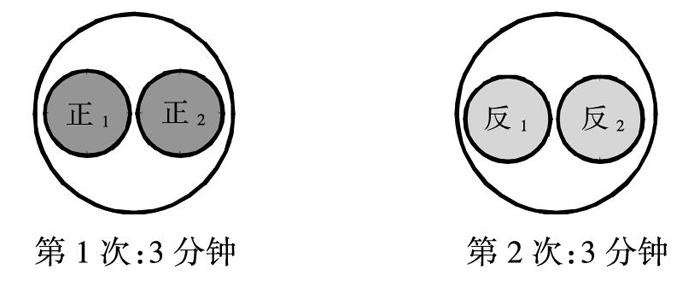
【争议的环节】操作印证规律，操作下图：

第1次：3分鐘 第2次：3分钟

正1=正2=0.5张 （半张）饼子 反1=反2=0.5张（半张）饼子

正1+正2=1张饼子 反1+反2=1张饼子

总之，1张饼2个面，亦即2个面相当于1张饼，每次同时烙饼2张（实质是2面），2面就是2个半张饼，相当于每次1张饼最少3分钟。

3.烙3张饼（分析推理—实践操作—画图记录）

（1）猜测与操作：学生认为有18分钟、12分钟，都有锅空情况，不是最少时间，最少时间应为多少？

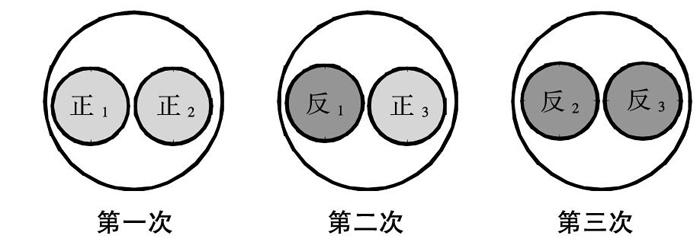
（2）推理与操作：师提示规律：次数等于张数，“1张饼烙1次（1个3分钟）最少3分钟”，学生：3张饼有6个面，每次烙2个面，需要3次，次数等于张数，“3张饼烙3次（3个3分钟）最少9分钟”，操作图示如下：

4.烙多张饼（应用规律）

重点是两个：A.一是烙饼需要的最少时间；B.二是最省时的烙饼过程与方式。

烙饼4张：

学生先推理：按照规律，4张饼烙4次，4个3分钟是12分钟；或4张一共烙8面，每次烙2面，烙饼4次。烙饼的过程与方法：2张2张烙，2个2张，2个6分钟也是12分钟。

烙饼2-4张小结：

通过列表印证规律：

A.次数等于张数，“1张饼烙1次（1个3分钟）最少3分钟”。

B.还发现：总时间是张数的3倍，所以，烙饼最少时间=张数×烙一个面的时间

（1）烙饼5张：应用规律得知需要5次，5个3分钟是15分钟。（过程与方法略）

（2）烙饼6张：应用规律得知需要6次，6个3分钟是18分钟。（过程与方法略）

（3）烙饼7张：应用规律得知需要5次，7个3分钟是21分钟。（过程与方法略）

（4）烙饼8张、9张、10张……学生很容易推理计算和叙述烙饼的过程与方法。

烙饼很多张饼，应用规律来解答，无须重视烙饼的过程与方法，操作也不必。例如：

烙20张最少20次，20个3分钟60分钟； 烙100张最少100次，100个3分钟300分钟：烙200张最少200次，200个3分钟600分钟......

二、分歧

1.与众不同

这部分教学内容，我听课多次，有名师的课，有竞赛的优质课等等；也学习过很多人的教学设计；这课我也教学过或上过示范课。但是都没有像我这次这样新的尝试：融合了“规律”这个元素，或者说“规律”贯穿着课程的始终，而且伴随着分析推理。

2.教研员不赞同

教研员在评课时指出“没有必要找出规律来解决问题”，其余听课者也众说纷纭，争论不下，也就没了最终的结论。

三、我的观点

教后反思，笔者就数学里的规律问题做了一定研究，笔者以为：

1.规律是数学的灵魂

数学教学中，规律无处不在，无时不在，数学离不开规律。只不过有些规律是隐性规律，有些是显性规律，有些是按规律解决问题，有些规律需要去发现并强化。在这里，多数人认为不必找寻发现规律，更不必强调规律，而我认为有必要发现规律，强调规律，是显性规律。

2.规律是思维的路径

规律和数量关系也是一种逻辑关系，符合逻辑的思维才是真正的思维，思维必须要符合逻辑，有时必须找到规律或数量关系，思维才能进行下去。不思考规律或不按照规律去思考，就会失去思考的方向，思维就无从入手。

3.规律是计算的依据

有一组相关联的数据，也就有规律存在，即存在等量关系，也就是有了计算的依据。学生结合先前时间操作，烙饼1张和2张分别都是6分钟，烙饼一共3张，时间一共12分钟，学生也明白烙饼1张浪费了时间，不是优化；1张1张的烙饼，烙饼3张一共18分钟，也不是优化；有没有更少的时间完成烙饼3张，学生很难得到需要多少分钟，即便想到9分钟，也仅仅是猜测，没有理论依据；如果是按照规律：烙饼每张3分钟，学生有了理论依据，就不难算出3张饼一共应该是9分钟。

4.规律是实践的目标

按照规律，算出3张饼一共应该是9分钟，实践操作就要去证明理论计算是正确的，操作实践就有了目标方向。学生操作实践证明有一定的难度，但是，如果提示了规律，学生很容易想到：3张饼6个面，每次2个面，需要3次，得到次数等于张数，每次的2个面只需要轮换即可。

因此，我认为：操作伴随着规律的思考是最有效的操作，是理论与实践完美的结合。纯粹的理论不能判定结论正确与否；纯粹的实践就会失去目标与方向，而且操作很难奏效。操作伴随着规律的思考，操作实践证明了理论思考的正确性，理论思考反过来证明操作实践也是正确的，两者结合，是学习数学的有效途径。

5.规律是年级的特点

从四年级开始，规律现象更加突出，更加凸显，这是一种教学方向，也是一种教学的趋势。本教材内容是四年级最后章节，这应该是运用规律来解决问题的时候了。

根据以上的阐释，我认为本节内容有必要应用规律来解决问题。

编辑 谢尾合