深空探测器模块化结构动力学研究

于登云，张玉花，褚英志，李昊，王建炜，杜冬

（1. 中国航天科技集团公司，北京 100048；2. 上海航天技术研究院，上海 201109；3. 上海卫星工程研究所，上海 200240）

深空探测器模块化结构动力学研究

于登云1，张玉花2，褚英志2，李昊3，王建炜3，杜冬3

（1. 中国航天科技集团公司，北京 100048；2. 上海航天技术研究院，上海 201109；3. 上海卫星工程研究所，上海 200240）

随着深空探测器技术的不断发展，深空探测器设计逐渐转向模块化和标准化。串联结构是模块化深空探测器常见并较为合理的结构形式，而如何将运载对探测器整体模态频率的指标要求合理转化为对探测器各个模块结构的设计要求是当前工作中的一项挑战。根据子结构综合模态法并基于固定边界法和悬臂梁理论，提出了探测器子结构模块动力学模态指标的分配方法。采用3种子结构模块极限处理方法，用全解析方式推导了子结构模块的基频表达式，并分析了子结构模块的动力学特性与探测器整体结构动力学特性之间的关系。提出的子结构模块的动力学指标分解方法操作简单，精度较高，可为串联式模块化深空探测器的设计提供关键性的指导。

深空探测器；模块化；子结构；动力学；指标分解

引用格式：于登云，张玉花，褚英志，等. 深空探测器模块化结构动力学研究［J］. 深空探测学报，2016，3（3）：268-274.

Reference format: Yu D Y，Zhang Y H，Chu Y Z，et al. Structure dynamics analysis of modularized deep space detector［J］. Journal of Deep Space Exploration，2016，3（3）：268-274.

0　引　言

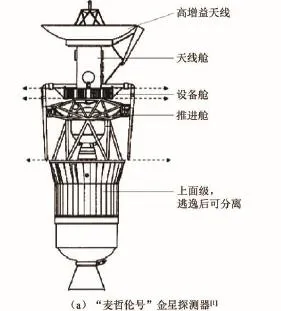
随着航天技术的不断发展，航天器结构设计逐渐转向模块化、标准化。在深空探测领域，执行深空探测任务往往需要同时具备轨道转移功能、轨道进入功能和科学试验功能，所以通常设置不同独立模块完成相应功能。受运载包络空间的限制，模块化串联结构成为深空探测航天器的典型形式。例如1989年美国发射的“麦哲伦号”金星探测器，俄罗斯与中国联合研制的“福布斯”与“萤火1号”火星探测器组合体，以及拟于2022年发射的金星气候探测器都是典型的模块化串联结构，如图1所示。

航天器结构动力学的基本任务是分析研究航天器结构的固有特性（包括模态频率和模态振型），以及在外载激励下的动力学响应，包括结构模态分析、动静强度计算、刚度分析、响应分析与结构优化等。航天器结构动力学分析的目的是：1）为航天器结构与机构优化设计与试验提供预示和设计依据。2）为运载火箭提供星箭模态综合与试验的全星结构动力学特性。3）为全星与结构振动有关的各类耦合动力学分析提供附件级乃至全星级结构模态参数等［2］。

航天对结构设计各方面的要求都极为苛刻，其中模态参数等是航天器设计极为关键的参数，这些参数的精确性与可靠性决定了航天器控制系统是否能正常工作，这些参数的错误会造成控制的错误，使航天器因无法正常飞行而失败。因此航天器结构动力学的研究具有重要意义。在工程应用中，对于复杂的航天器结构，通常可以分解成若干个比较简单的子结构。复杂结构的子结构分析法通过对各个子结构的动态特性进行综合，并利用子结构间的边界条件，最终得到整个结构的动态特性。

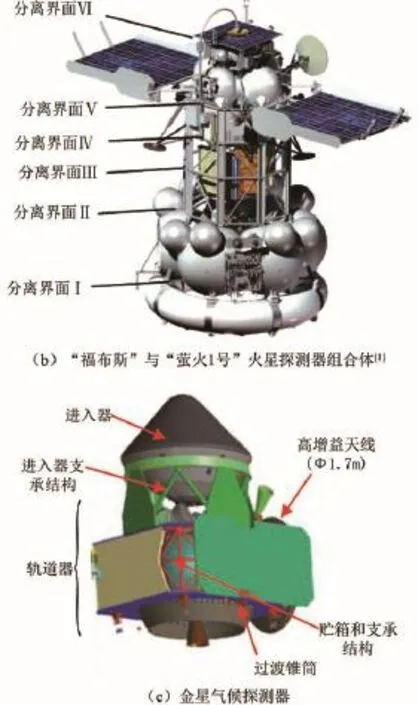
图1　模块化串联结构深空探测器Fig.1　Modularized series-connected deep space detectors

1　航天器结构动力学子结构模态分析方法

自20世纪60年代初Hurty（1960）［3］和Gladwell（1964）［4］奠定模态综合技术以来，子结构方法［5-7］已广泛应用于航天航空和各种大型工程领域，这是一种复杂结构建模与分析的有效方法。采用这种方法通过模态坐标变换可以把结构动力学问题化为缩聚自由度的问题，从而大大简化计算，提高分析效率。动态子结构方法［8-9］以瑞利-李兹法（Rayleigh-Ritz）为理论基础，并在20世纪60年代由Hurty和Gladwell等人提出模态综合技术后蓬勃发展，经Craig和Bampton等学者改进完善后，目前已广泛用于航空航天等工程领域。

动态子结构方法的基本思想是按照工程的观点或结构的几何轮廓，在遵循某些原则要求的基础上，把完整的大型复杂结构人为地抽象成若干个子结构，首先对各子结构进行凝聚得到其主要模态信息，然后再综合得到总体结构的动态特性。动态子结构法在大大降低结构自由度的基础上，保留了结构的动态特性信息。一方面，能够以较少的时间和资源成本解决大型结构系统的动力学计算问题；另一方面，在模态坐标下给出有限元模型的动态特性信息，能够屏蔽结构设计参数等技术秘密，便于企业间和国际间合作的开展。

动态子结构模态综合法按照对界面的处理方法，分为自由界面法、固定界面法和混合和综合界面法。自由界面法将子结构的界面自由度完全放松，利用子结构的模态来构造变换，通过界面协调条件来得到整体结构的缩聚系统。自由界面法由于综合方程不包含界面自由度，所以自产生之初一直备受关注。Hou（1969）［10］和Goldman（1969）［11］于1969年分别提出了自由界面法。由于子结构的低阶主模态只对总体结构的低阶模态有较大影响，因此Hou和Goldman只采用低阶主模态为基础来描述子结构的运动。初始的基于低阶模态的子结构法由于未考虑高阶模态，计算精度较差。在自由界面法的后续发展中，Macneal（1971）［12］、Rubin（1975）等［13］考虑了高阶模态的影响，大大提高了自由界面法的计算精度。固定界面法通过在子结构的连接面上施加固定约束，以此结构的主模态和约束模态构造整体结构的综合模态。Hurty（1960）［14］首先提出了模态坐标和模态综合法的概念，奠定了固定界面法的基础。Craig和Bampton对Hurty的方法进行改进，认为应将复杂结构的模态分为主模态和约束模态两部分。改进的方法拥有综合精度高和编制程序方便的优点，因此被广泛使用［15］。Craig和Chang（1977）［16］针对固定界面法自由度较多的缺点，提出了3种自由度减缩方法，分别是主模态坐标减缩、Guyan减缩和Ritz减缩。混合界面法介于自由界面法和固定界面法之间，兼具两种方法的特点，可施加约束或解除约束来生成彼此独立的子结构，并分别予以综合。Benfield和Hruda（1971）［15］提出综合界面法。该方法按照某一界面固定而对应的另一界面自由的原则，将一个复杂结构分离成若干主从结构和从子结构。

随着航天器研制过程中部门间、企业间乃至国际间合作的增多，航天器各部件有限元模型的交互日益频繁。但考虑到保护其自身技术的需要，企业常常不愿将反映大量结构设计信息的有限元模型直接提供给合作方。迫切需要将有限元物理模型进行适当技术处理，在保留模型力学特性的情况下，屏蔽具体的设计信息。动态子结构分析方法的出现，能较好地解决上述问题。

2　基于子结构模态法的航天器模块模态指标设计

随着航天领域内的合作与分工日益复杂化，模块化航天器各个模块又往往分属于不同研制单位，如果能够将整器模态要求合理分配成各个模块的结构设计指标，则对于任务的分解和总体集成极富应用价值。因此，模块化航天器的设计过程中，需首先确定不同模块的各自模态频率与航天整体结构模态频率之间的定量化关系。在运载限定整器模态频率下限的情况下，合理分配各自的设计指标对于各个模块的结构设计具有重要意义。

悬臂梁结构与串联模块化探测器的发射状态极为相似，本研究基于悬臂梁假设，探索串联结构基频的快速估算方法，可为总体指标分解与集成提供有益的技术支持。目前，航天领域内对于深空探测器结构动力学设计的惯用做法是由各个研制单位提供各自负责模块的有限元模型，经总体复核整器模态特性后作为实物研制的参考依据。这种设计方法的缺点是，以有限元模型作为参考依据可操作性较差，尤其难于通过各个模块单独的力学试验考核设计的合理性，研制任务书中无法提炼出关键性的技术指标，实际上也就造成了盲目设计，一旦出现整器模态频率不达标，往往不能明确划分各方的责任界限。

2.1串联结构理论建模

针对串联型结构，为简化分析，得到更为普适的解析解，将串联结构的基础模块和附加模块假设为串联的两段悬臂梁，如图2所示。

图2中，梁Ⅰ代表基础模块，梁Ⅱ代表附加模块。两段梁的线密度分别为ρ1和ρ2，抗弯刚度分别为E1I1和E2I2，长度分别为a和b。悬臂梁总长度为l，根据图中所示应有

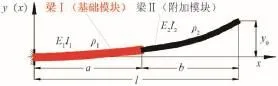
图2　悬臂梁模型示意图Fig.2　Sketch map of cantilever model

按照经典分析方法，可假定悬臂梁基频振型与悬臂梁受惯性过载产生的静变形曲线完全一致。设悬臂梁的末端位移为y0。不难计算悬臂梁的静变形曲线为（推导过程较为复杂，限于篇幅，此处仅列出结果）

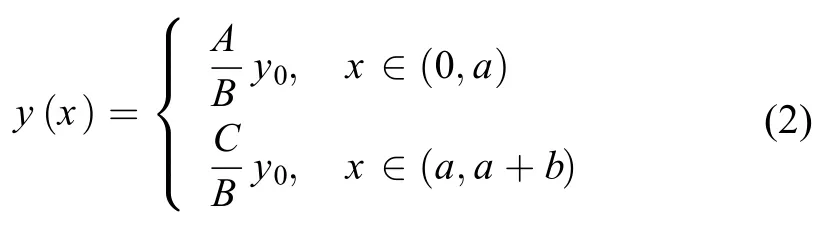
其中

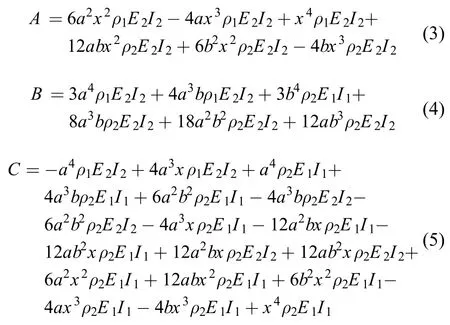
根据简单梁假设，悬臂梁最大弹性势能为

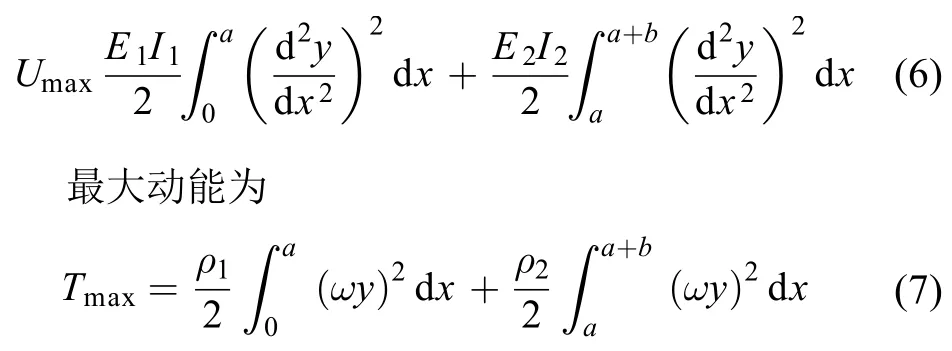
将式（2）～（5）代入式（6）、（7），并利用瑞利原理，令

式（9）、（10）代表了一般情况下串联结构基频的解析解。为检验解析解的正确性，取一种最简单的情况，即两端悬臂梁的抗弯刚度和线密度完全相同，此时

将式（15）代入式（11）、（12）和式（9），最终得到

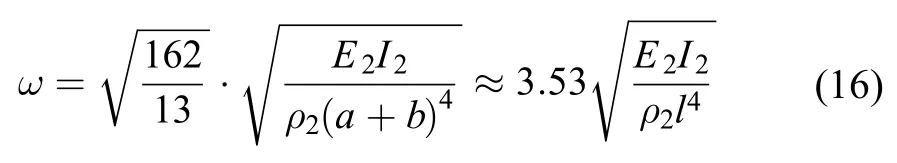
或者，令梁Ⅰ的抗弯刚度E1I1无穷大，则悬臂梁退化为梁Ⅱ，此时

将式（17）代入式（9），可得

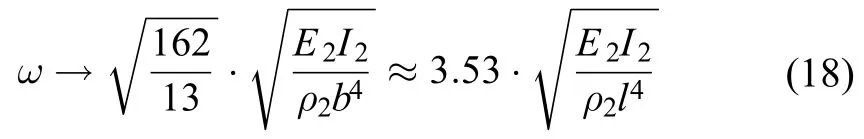
长度为L，抗弯刚度为EI，线密度为ρ的悬臂梁基频之精确解为

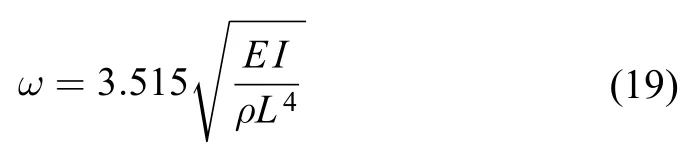
式（16）、（18）和式（19）的误差在0.43%之内，可见上述利用假设振型并通过瑞利原理计算基频的近似方法精度是相当高的。

2.2模型研究

从力学角度作定性考虑，图2所示串联式悬臂结构的一弯模态中，梁Ⅰ作为基础模块大体上是以刚度单元参与作用的，梁Ⅱ作为附加模块大体上以质量单元参与作用。为便于比较，将模型作3种极限处理。

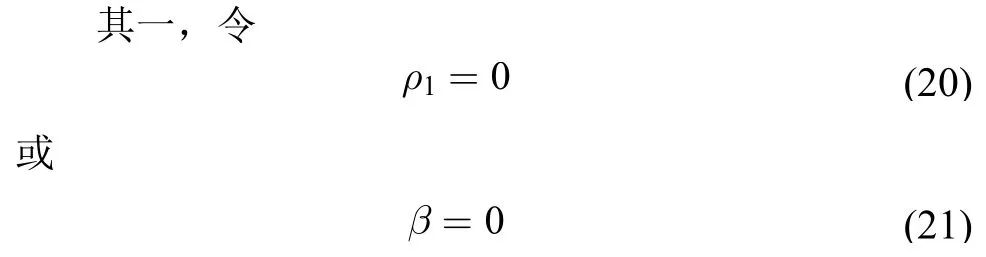
将式（21）代入式（11）、（12）和式（10），最终得到

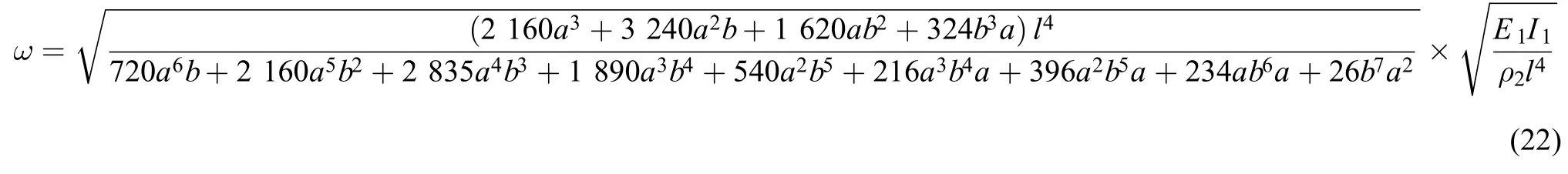
此时梁Ⅰ（基础模块）仅具有刚度特性（既有线刚度，又有角刚度）。

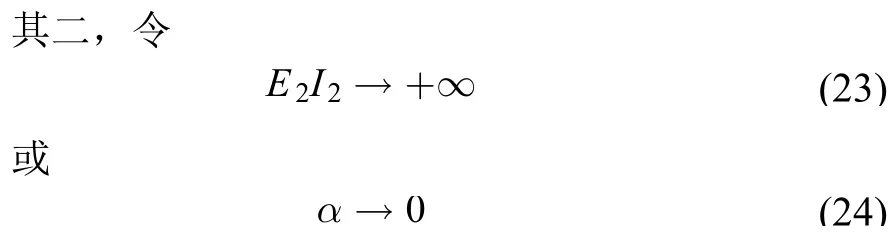
将式（24）代入式（11）、（12）和式（10），最终得到

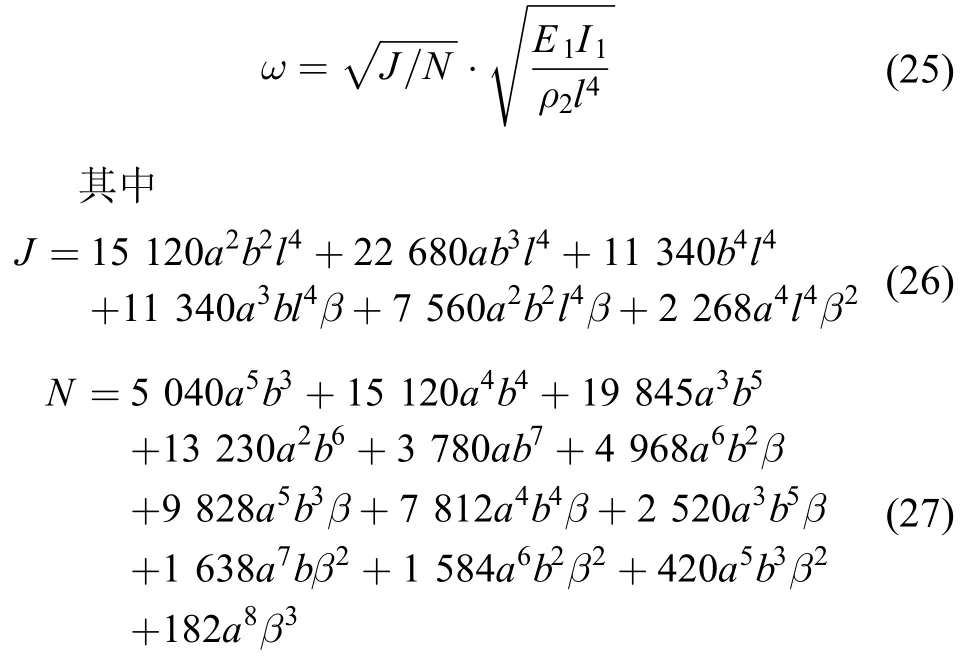
此时梁Ⅱ（附加模块）仅具有质量特性（包括质量、质心以及惯量3个特性）。

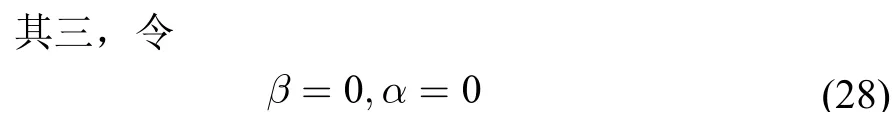
将式（28）代入式（11）、（12）和式（10），最终得到

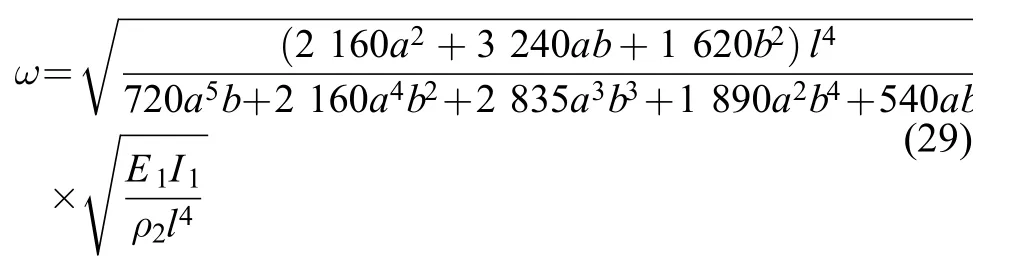
此时梁Ⅰ（基础模块）仅具有刚度特性，梁Ⅱ（附加模块）仅具有质量特性。

2.3比较与分析

为显示真实情况（见式（10））与3种极限处理方法（见式（22）、（25）、（29））之间的差异，取4个频率解析式中无量纲部分，即

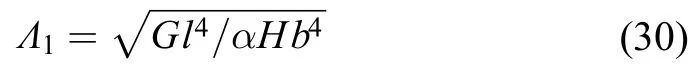
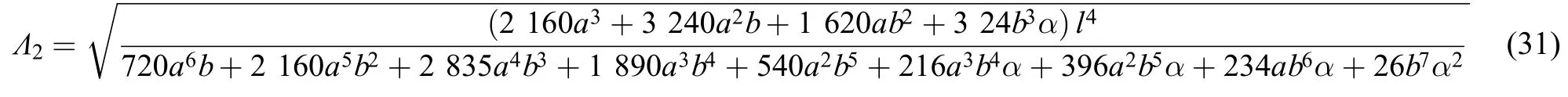
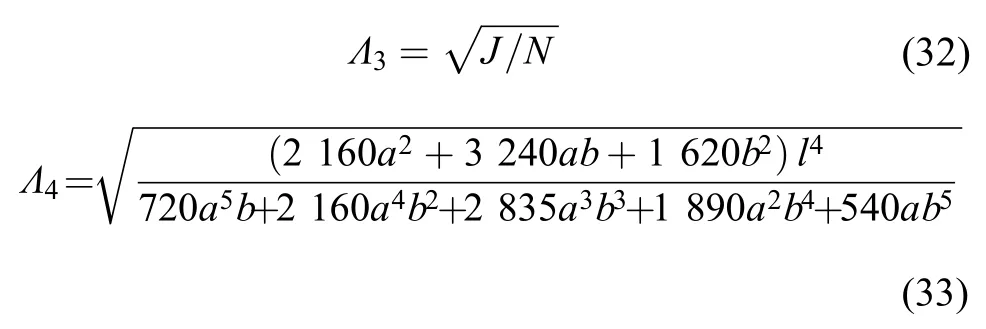
并考虑基础模块（梁Ⅰ）与附加模块（梁Ⅱ）刚度、质量密度的差异（即不同的α、β），列于图3中。横轴为，即基础模块高度所占的比例。考虑到工程中可能的情况，分别列举了α取10、1、0.1和β取10、1、0.1的组合，总计9种状态。

对图3分析如下。

1）图3（a）～（h）显示，仅考虑基础模块（梁Ⅰ，下同）的刚度特性，忽略质量特性，同时仅考虑附加模块（梁Ⅱ，下同）的质量特性，忽略刚度特性，这种处理方法与真实情况误差最大，不推荐作为串联结构基频估算方法。不过图3（i）表明，当且仅当基础模块刚度较大，同时附加模块质量较大时，该方法计算误差较小。还应当看到，这种估算方法得到的无量纲曲线具有平坦的“谷底”，相对而言，该区域与真实情况接近——在对模块更详细的模态信息无从知晓的情况下，不妨将“谷底”区域作为初步的近似计算手段。

2）仅考虑基础模块的刚度特性，忽略其质量特性，如果基础模块高度占整体结构高度比例不太大，该方法与真实情况误差较小，见图3（d）～（f）。如果基础模块刚度较附加模块大很多，则即便基础模块高度比例偏大，该方法也可能有效，见图3（a）～（c）。

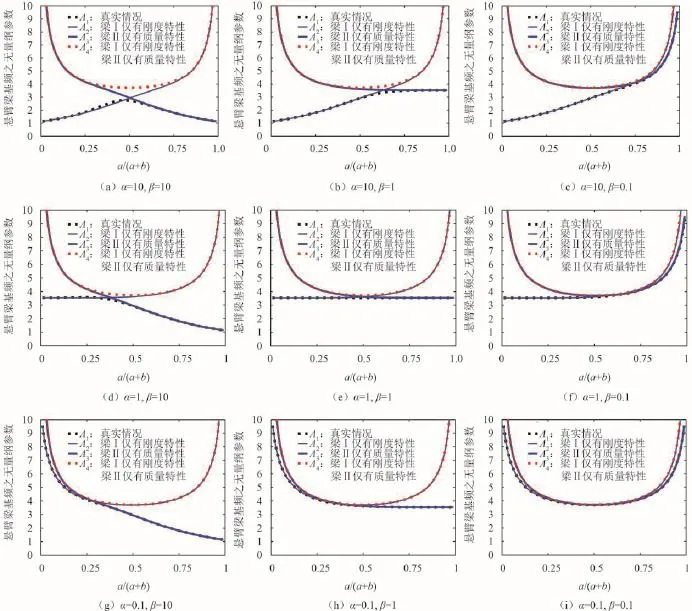
图3　串联式结构模态频率计算方法比较Fig.3　Comparison of model frequency prediction using different method

3）仅考虑附加模块的质量特性，忽略其刚度特性，如果附加模块高度占整体结构高度比例不太大，该方法与真实情况误差较小，见图3（a）、（b）、（d）、（e）、（g）、（h）。如果基础模块质量较附加模块大，那么即便附加模块高度比例偏大，该方法也可能有效，见图3（g）～（i）。

4）从图3中总结得到

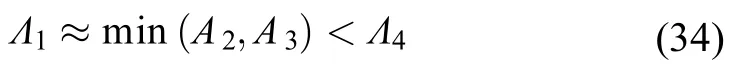
也就是说，可以将考虑基础模块的刚度特性并忽略其质量特性的极限情况、考虑附加模块的质量特性并忽略其刚度特性的极限情况作为串联结构模态频率的简单估算方法。真实频率就是两种极限处理方法的最小下界，其误差不超过5%。

上述分析的第4条可作为串联式结构模态频率总体指标分解的重要依据，具体操作方法如下。

首先，在对运载提出的模态频率指标分解之前，应该估算附加模块的质量特性（质量、质心和惯量）以及整星外形基本尺寸，利用单自由度弹簧振子原理，根据质量特性和运载模态频率要求估算基础模块与附加模块连接界面的刚度矩阵，此刚度矩阵为基础模块整体的静刚度参数，包含线刚度、角刚度以及耦合刚度。估算的附加模块质量特性与基础模块刚度矩阵是对研制方的输入内容；然后，对研制方提出要求。

对基础模块结构研制方的要求如下。

1）基础模块在顶部连接了质量特性与附加模块完全相同的刚体之后，基频应高于运载要求。

2）基础模块结构与附加模块连接界面处的静刚度矩阵元素绝对值必须大于估算的静刚度矩阵。

对附加模块结构研制方的要求如下。

1）附加模块在底部连接了刚度矩阵与估算刚度矩阵相同的弹性单元（无质量）之后，基频应高于运载要求。

2）附加模块的质量、质心、惯量等数据与估算质量特性之间的误差不得大于5%。

如果基础模块结构研制方能够满足总体要求，则Λ3满足基频要求。如果附加模块研制方能够满足总体要求，则Λ2也满足基频要求。根据式（34），Λ必然也满足运载要求，其误差在5%以内。为保证指标可靠性，总体部门在实际下达频率指标要求时可适当留有一定余量。

针对具有多个模块的串联结构，该方法也可采用递归方式予以推广。以三模块串联（即上、中、下模块串联）为例，可先定义上部模块为附加模块，中、下部模块整体作为基础模块，完成双串联结构频率指标分配后，将得到的基础模块频率指标作为中下部模块的总体指标，进行再分配，得到中下部两模块各自的频率指标。必须指出，多次递归式的误差可能将增加。

3　结　论

本文对模块化航天器设计中的子结构动力学分析方法进行研究，并基于子结构模态综合法，提出了一种对两模块串联航天器结构各个模块指标进行分配的设计方法，即利用两种极限情况拟合真实结构的模态频率，其误差在5%以内。该方法可以为总体分配探测器两个模块结构设计指标，或者分配星体结构与大型有效载荷结构设计指标提供关键性支持。

［1］张伟，方宝东，成玫，等. 空间飞行器分离式构型设计［J］. 上海航天，2013，30（1）：1-7. Zhang W，Fang B D，Cheng M，et al. Design of separation configuration for spacecraft［J］. Aerospace Shanghai，2013，30（1）：1-7.

［2］黄文虎，曹登庆，韩增尧. 航天器动力学与控制的研究进展与展望［J］. 力学进展，42（4）：68-76. Huang W H，Cao D Q，Han Z Y. Advances and trends in dynamics and control of spacecrafts［J］. Advances in Mechanics，42（4）：68-76.

［3］Hurty W C. Vibrations of structural systems by component mode synthesis［J］. Journal of the Engineering Mechanics Division，ASCE，1960，86（4）：51-70.

［4］Gladwell G M L. Branch mode analysis of vibrating systems［J］. Journal of Sound and Vibration，1964，1（1）：41-59.

［5］王文亮，杜作润. 结构振动与动态子结构方法［M］. 上海：复旦大学出版社，1985. Wang W L，Du Z R. Structural vibration and dynamic substructure method［M］. Shanghai：Fudan University Press，1985.

［6］殷学刚，陈淮，塞开林. 结构振动分析的子结构方法［M］. 北京：中国铁道出版社，1991. Yin X G，Chen H，Sai K L. Substructure method for structural vibration analysis［M］. Beijing：China Railway Publishing House，1991.

［7］郑兆昌. 复杂结构振动研究的模态综合技术［J］. 振动与冲击，1982（1）：28-36. Zheng Z C. The study on vibration of complex structure systems by component mode synthesis techniques［J］. Journal of Vibration and Shock，1982 （1）：28-36.

［8］宋景涛，方明霞. 模态综合法在ANSYS中的应用［J］. 计算机辅助工程，2007，16（3）：145-148. Song J T，Fang M X. Application of component mode synthesis in ansys［J］. Computer Aided Engineering，2007，16（3）：145-148.

［9］王永岩.动态子结构方法理论及应用［M］. 北京：科学出版社，1999. Wang Y Y. Theory and application of dynamic substructure method［M］. Beijing：Science Press，1999.

［10］Hou S N. Review of modal synthesis techniques and a newapproach［J］. Shock Vib. bull ，1969，40（4）：25-39.

［11］Goldman R L. Vibration analysis by dynamic partitioning［J］. AIAA J，1969，7（6）：1152-1154.

［12］MacNeal R H. A hybrid method of component mode synthesis［J］. Computers Structures，1971，1（4）：581-601.

［13］Rubin S. Improved component-mode representation for structure dynamic analysis［J］. AIAA J，1975，13（8）：995-1006.

［14］Hurty W C. Vibration of structure by component mode synthesis［J］. J. Engr. Div.，ASCE，1960，86：51-59.

［15］杜飞平，谭永华，陈建华，等. 航天器子结构模态综合法研究现状及进展［J］. 力学进展，2010，36（3）：39-62. Du F P，Tan Y H，Chen J H，et al. Status and progress on substructural modal synthesis techniques for space vehicls［J］ Advances in Mechanics，2010，36（3）：39-62.

［16］Craig R R，Chang C J. On the use of attachment modes in substructure coupling for dynamic analysis［C］. AIAA/ASME 18th Struct. Dyn. and Materials. Conf.，SanDiego，CA：1977.

通信地址：北京市海淀区阜成路16号航天科技大厦（100048）

电话：（010）68370292

E-mail：yudyun@sina.com

Structure Dynamics Analysis of Modularized Deep Space Detector

YU Dengyun1，ZHANG Yuhua2，CHU Yingzhi2，LI Hao3，WANG Jianwei3，DU Dong3
（1. China Aerospace Science And Technology Corporation，Beijing 100048，China；2. Shanghai Academy Of Spaceflight Technology，Shanghai 201109，China；3. Shanghai Institute Of Satellite Engineering，Shanghai 200240，China）

Modularized and standardized concepts of deeps pace detectors are increasing along with the development of deep space exploration technique. Series connection between different sub-modules of deep space detectors are reasonable and popular，and it is a challenge to propose a reasonable dynamic response index for a single sub-module according to the dynamic response index of the overall series-connected structure. Based on the substructure modal synthesis method and the cantilever beam theory， It proposes a method for assigning design index of dynamic response for sub-modules of series-connected structures. The equation of fundamental frequencies of sub-modules are derived analytically based on three consumptions，and the relation between the dynamics of sub-modules and that of overall series-connected structure are discussed. The proposed dynamics index assignment method shows high accuracy and can provide critical instructions for the design of series-connected modularized deep space detectors.

deep space detector；modularize；sub-structure；dynamics；index assignment

V476

A

2095-7777（2016）03-0268-7

10.15982/j.issn.2095-7777.2016.03.011

于登云（1961- ），男，研究员，博士生导师，中国航天科技集团公司科技委副主任，中国探月工程副总设计师，主要研究方向：航天器动力学与总体设计技术。

［责任编辑：杨晓燕］

2016-04-20；

2016-05-21