深空探测光学导航敏感器在轨几何定标方法

程宇峰，润一，王密

（武汉大学　测绘遥感信息工程国家重点实验室，武汉 430079）

深空探测光学导航敏感器在轨几何定标方法

程宇峰，润一，王密

（武汉大学测绘遥感信息工程国家重点实验室，武汉 430079）

光学导航敏感器是光学自主导航的一个核心器件，它所获得的导航目标源的光线指向的精度将直接影响自主导航的精度。设计了一个分步式的光学导航敏感器在轨几何定标方法，该方法先求解外定标参数，然后在外定标所确定的广义相机坐标系下求解内定标参数，从而完成对内外定标参数的标定。为了在星上计算资源与能力有限的环境下，利用更多的参考星图实现对定标参数的高精度估计，利用逐行法化最小二乘方法估计定标参数。实验表明，通过高精度的在轨几何定标，可以有效提高光学导航敏感器的指向量测精度，使其满足光学自主导航的需求。

导航敏感器；几何定标；逐行法化；最小二乘

引用格式：程宇峰，润一，王密. 深空探测光学导航敏感器在轨几何定标方法［J］. 深空探测学报，2016，3（3）：228-236.

Reference format: Cheng Y F，Run Y，Wang M. On-orbit calibration approach for optical navigation sensor in deep space exploration ［J］. Journal of Deep Space Exploration，2016，3（3）：228-236.

0　引　言

光学天文导航是一种有效的深空自主导航方式，主要解决由于飞行器与地球距离过远造成的地面控制指令通信延迟或者中断问题［1］。光学天文导航主要利用光学导航图像来获取导航信息。通常情况下，探测器利用光学导航敏感器对轨道附近的目标天体如行星、彗星、卫星、小行星或其他飞行器等进行拍摄成像，通过图像处理的方法提取导航图像中的目标源，利用目标源先验的轨道信息与图像坐标，计算出飞行器到目标源在惯性坐标系中的光线矢量，将其作为导航定位的重要输入，与其他姿控观测量进行组合滤波，最终实现飞行器的自主导航定位［2-3］。

飞行器到导航目标源的光线矢量是自主导航中最重要的观测输入，它的精度主要由光学导航敏感器的精度决定，并直接决定最终导航定位的精度［4］。当光学导航敏感器进行拍摄成像时，姿控系统输出系统相对于惯性系的姿态，通过导航敏感器与姿控系统的刚性安装关系（如图1所示），可以将量测于相机坐标系下的光线矢量转化到惯性系中，最终输入到制导、导航、控制系统中［5］。虽然导航敏感器在地面上已经进行了严格的标定［6］，包括相机的内部畸变标定与相机的安装关系标定，但是由于发射过程中的震动以及运行过程中环境的变化，地面的标定参数通常会发生变化，因此，为了确保导航的精度，光学导航敏感器的在轨几何定标具有重要的意义［7］。然而，国内外却鲜有这方面的研究报道。

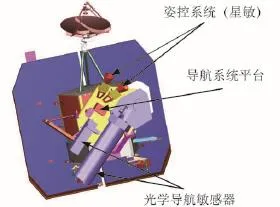
图1　深度撞击探测器导航系统平台设计示意图Fig.1　The design sketch of the deep impact spacecraft navigation system platform

本文提出了一种分步式光学导航敏感器在轨几何定标方法，先估计外部安装参数，然后在外部参数的基础上估计内部畸变参数。导航图像中的背景恒星可以通过星图识别的方法进行识别，获取其赤经赤纬信息，并作为解算几何定标参数的控制点。为了克服严格模型存在的过度参数化、强相关性以及低显著性问题，本文提出了一种二维指向角模型；同时为了克服星上计算存储能力有限的问题，提出了采用逐行法化最小二乘的方法进行参数解算。经过在轨定标，导航敏感器的每个像素都可以获得由姿控系统传递而来的精确的惯性指向，这样不仅可以确保光线矢量的量测精度，同时可以为导航图像中目标源的检测与识别提供先验的几何约束信息，从而大大减小图像处理与星图识别的难度。

1　光学导航敏感器的量测模型

光学导航敏感器的成像模型可以被视为小孔成像模型［8-9］，即拍摄目标的每一点放射的光线与焦平面上的各像素一一对应，如图2所示。

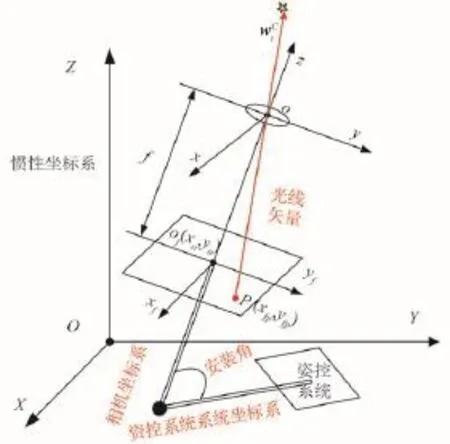
图2　光学导航敏感器的理想量测模型Fig.2　The ideal measuring model of optical navigation sensor

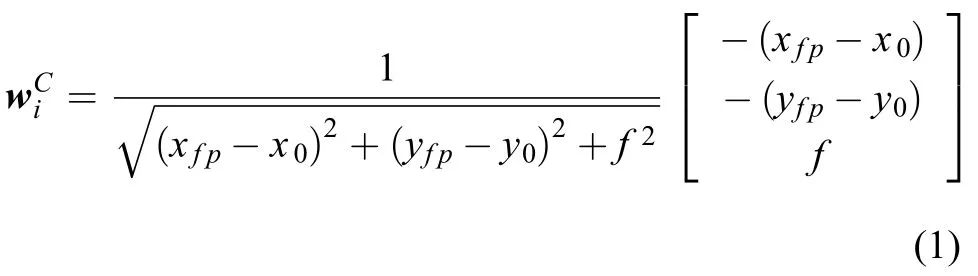
相机坐标系下的光线矢量可以根据姿控系统提供的姿态信息，结合安装关系转换到惯性坐标系中

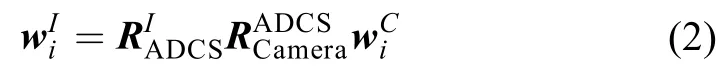
通常，导航敏感器在发射前已经在地面的高精度实验室中进行了精密的标定，但是器件的任何改变以及太空中环境的变化都会改变原有的相机参数，从而引入3种主要相机内部误差源：1）CCD焦面的平移、旋转、缩放；2）镜头光学畸变的改变；3）焦距的改变［10］。为了将导航目标源在相机坐标系下的量测坐标转换为实际坐标，这些误差必须要进行标定补偿。

1）CCD焦面的平移、旋转、缩放补偿

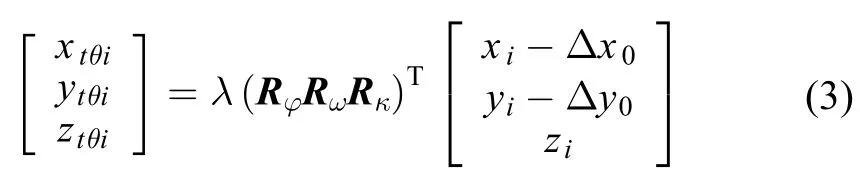
其中：Δx0与Δy0表示CCD的平移量，表示绕相机的y轴、x轴及z轴的旋转矩阵，表示缩放系数。

2）镜头的光学畸变补偿

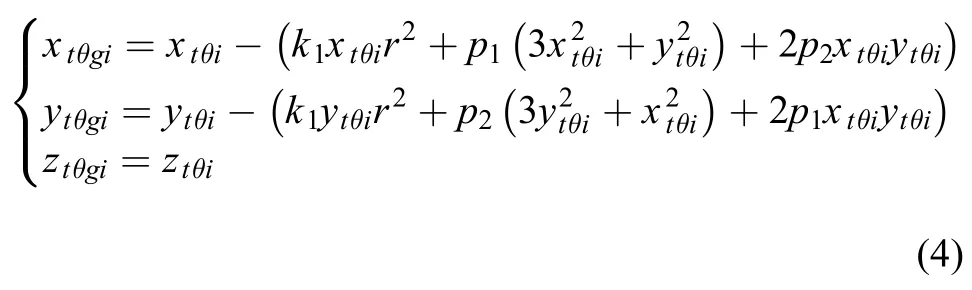
其中：k1表示径向畸变系数；p1、p2是切向畸变系数。3）焦距的补偿

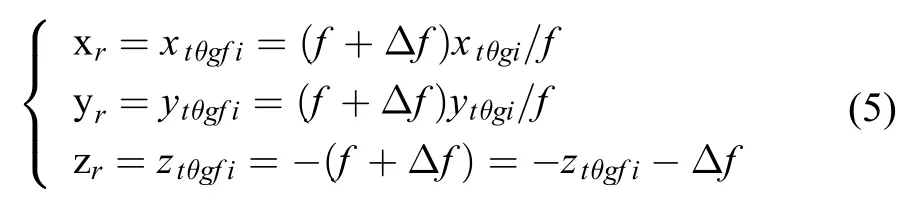
其中：Δf表示焦距的变化量。

式（3）～（5）可作为导航相机内部的严格物理成像模型。由于缺乏有效的温控方法，在轨运行过程中，相机的安装角相对于相机内部畸变更易受到环境变化的影响。假设相机安装角的地面标定值为（pitch，roll，yaw），（Δpitch，Δroll，Δyaw）为安装角的变化量，则真实的光线矢量由式（6）求得。

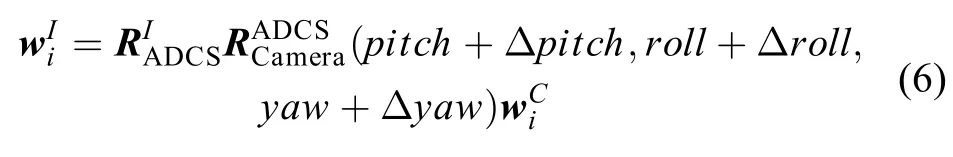
2　在轨几何定标模型

2.1几何定标模型

为了获得真实的导航量测模型，确保惯性系下光线矢量的指向精度，就必须对相机的安装角及内部畸变进行在轨定标。在轨定标可由以下两个步骤完成。

1）对相机安装角进行在轨定标。

2）在已定标的外部安装角的基础上，对相机内部畸变进行在轨定标。

导航图像中的背景恒星可以作为在轨定标的控制点信息。

2.1.1外定标模型

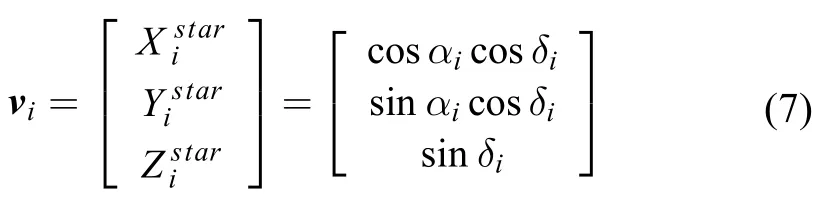
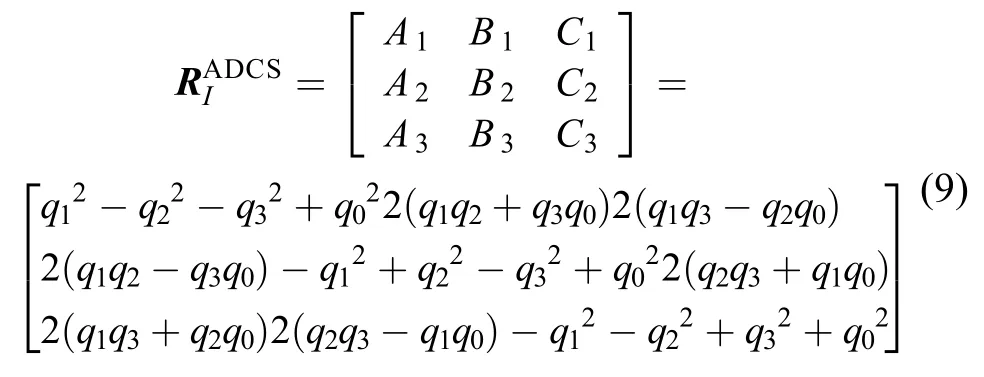
根据导航图像中识别的背景恒星，可以求解外定标参数XE（pitch，roll，yaw）。经过外定标，相机坐标系在惯性坐标系中的姿态可以由表 ?示，从而为内定标提供参考坐标系。

2.1.2内定标模型

尽管式（3）～（5）中的相机严格物理量测模型理论上考虑了大部分的内部畸变，但是由于其过度参数化，部分参数存在强相关关系，并且部分参数在图像定位精度方面存在低显著性等问题，如果直接将其作为内定标模型解算定标系数，会导致方程的病态问题，从而影响定标的精度。因此，严格物理量测模型虽然理论上具有严密性，但是其并不能直接作为在轨内定标模型。

为了克服这个问题，本文采用二维指向角模型［11］，如图3所示。通过检校每个像素在由外定标确定的参考坐标系下指向角的正切值，来恢复每个像素在惯性坐标系下的精确的光线指向。

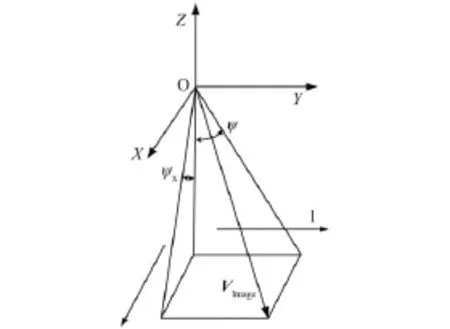
图3　相机二维指向角模型Fig.3　The two-dimension direction model of camera

多项式模型可以用来描述各指向角的正切值。由于导航敏感器的视场角较小，因此，具有高正交性与低相关性的三次多项式模型，可以作为导航敏感器的内定标模型。

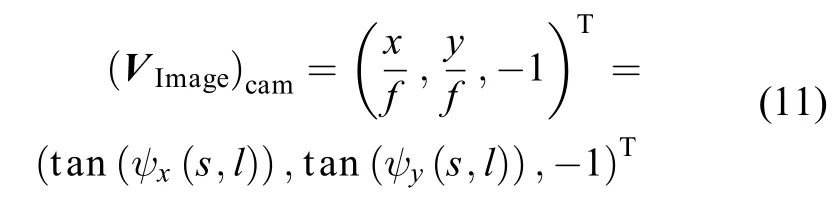
其中

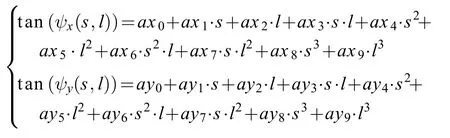
其中：（s，l）是像平面坐标系；ax0， ax1， ax2， ax3， ax4，ax5， ax6， ax7， ax8， ax9和ay0， ay1， ay2， ay3， ay4， ay5， ay6， ay7，ay8， ay9是内定标参数YI。

式（8）可以转换为

根据识别的背景恒星，内定标参数可以在外定标确定的安装矩阵的基础上进行解算。

2.1.3讨 论

如表1所示，外定标参数中的pitch角误差和内定标参数中的x0误差都会引起影像上的星点沿x轴平移；因此，pitch角和x0引起的误差具有相似性，二者具有强相关性；同理，roll角和y0，焦距f和径向畸变系数k1同样具有强相关性。由于内外定标参数具有强相关性，因此同时解算会导致法方程病态；因此，本文采用分步定标的方法解算内外定标参数。

在分步定标中，由于部分内部误差会引入到外定标的结果中，因此，通过外定标获得的参考坐标系并不是真正意义上的相机真实坐标系。但是，由于内定标参数具有高度的灵活性，且内定标参数与外定标参数之间存在高度的相关性，因此，并不会影响内定标的精度。同时，内定标参数还可以很好地补偿外定标过程中的残差，因此这也降低了对于外定标精度的要求。通过外定标参数与内定标参数的联合修正，可以高精度地恢复各个像素在惯性坐标系下的光线矢量。

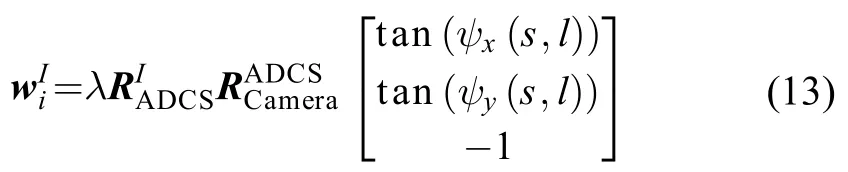
一旦内定标精确标定以后，由于其相对稳定的内部状态及需要较为复杂的计算量，因此不必经常更新。然而，外定标参数更加容易受到环境影响而变化，因此应尽量在每次拍摄导航目标源之前重新进行标定。

2.2定标参数解算方法

通过星图识别［12-13］方法，可以获得背景恒星的赤经、赤纬信息，从而获得其在惯性坐标系下的单位向量，背景恒星的像平面坐标可以通过质心提取［14-15］算法获得。这些正确识别的恒星可以作为定标参数解算的控制点。其中姿控系统输出姿态的偶然误差以及星点质心提取的误差是主要的随机误差源，需要尽可能地在解算的过程中进行消除。本文采用逐行法化最小二乘的方法，在不增加计算内存负担的前提下，使得更多的星图参与定标参数的估计，从而有效滤除噪声的影响。

实际上，首先通过逐行法化最小二乘的方法计算出外定标参数；然后基于外定标确定的参考系精确估计出内定标参数。在必要的时候，可基于内定标参数对外定标参数进行更新。

根据式（8）～（10）可推导出估计外定标参数的公式（14）：

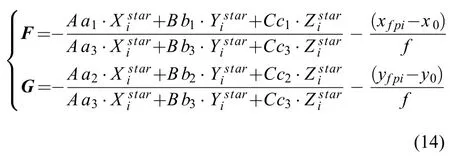
其中：F是相机坐标系下x方向的残差矢量；G是相机坐标系下y方向的残差矢量。

当内定标参数是待定参数时，式（12）是线性方程。因此，根据式（9）、（10）和式（12）可推导出估计内定标参数的式（15）。

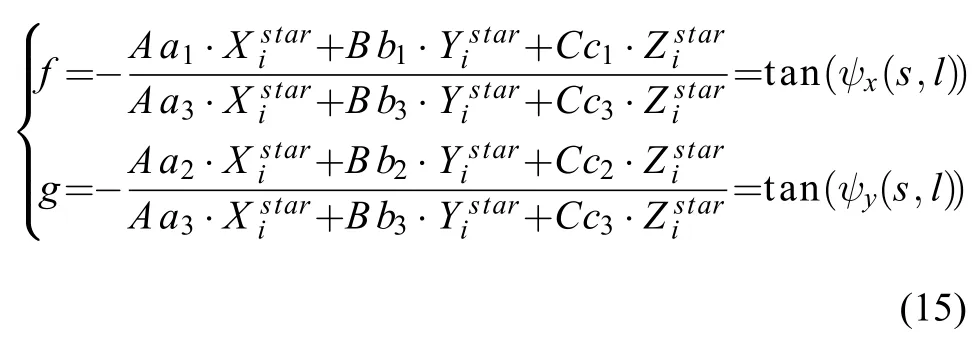
其中

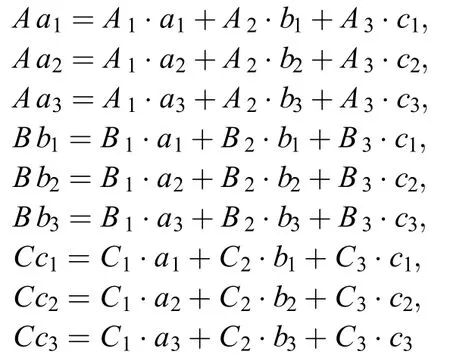
外定标参数为XE（pitch，roll，yaw），内定标参数为YI（ax0，…，ax9，ay0，…，ay9）。

2.2.1用逐行法化最小二乘的方法进行外定标

为了确定外定标参数，假设初始的内定标参数是“真值”。我们用地面定标初始值YI0和XE0作为内、外定标参数的初值。在外定标参数估计中，定义k为迭代次数，NE为每次迭代中参考恒星的数目。由于一幅影像中参考恒星的数目有限，我们选取连续拍摄的多张影像中的参考恒星来进行外定标参数估计。为了在增加参考恒星的数目的同时不增加计算内存的负担，本文采用逐行法化最小二乘的方法估计外定标参数。

将内、外定标参数的初始值（XE0，YI0）带入公式（14）并进行线性化，得到第k次迭代的公式（16）。

其中

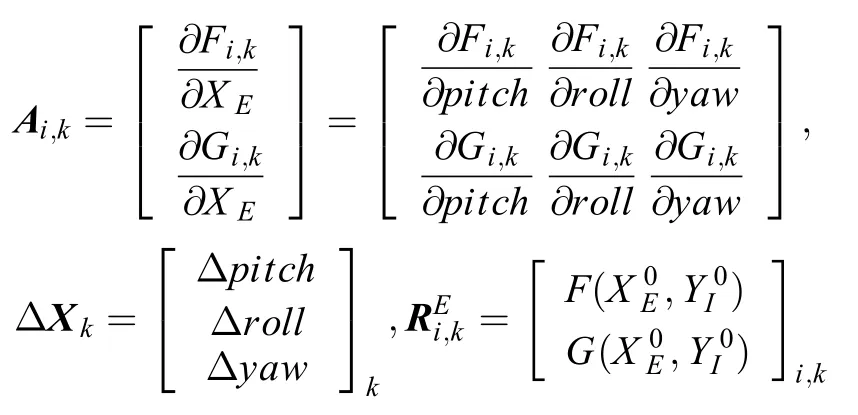
ΔXk是第k次迭代获得的外定标参数的改正数；Ri，kE是第k次迭代中根据当前的（XE0，YI0）计算出来的第i颗参考恒星的残差矢量，其中i = 1， 2， ···， NE。用最小二乘法可计算出

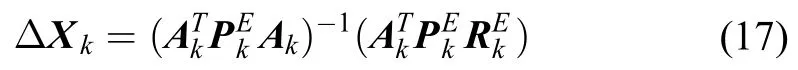
为了在增加参考恒星的数目的同时不增加计算内存的负担，本文采用逐行法化最小二乘的方法进行外定标。假设，，则有

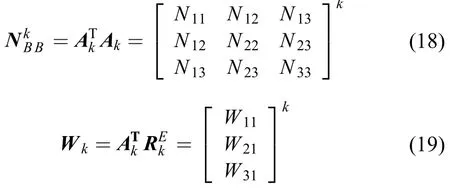
其中

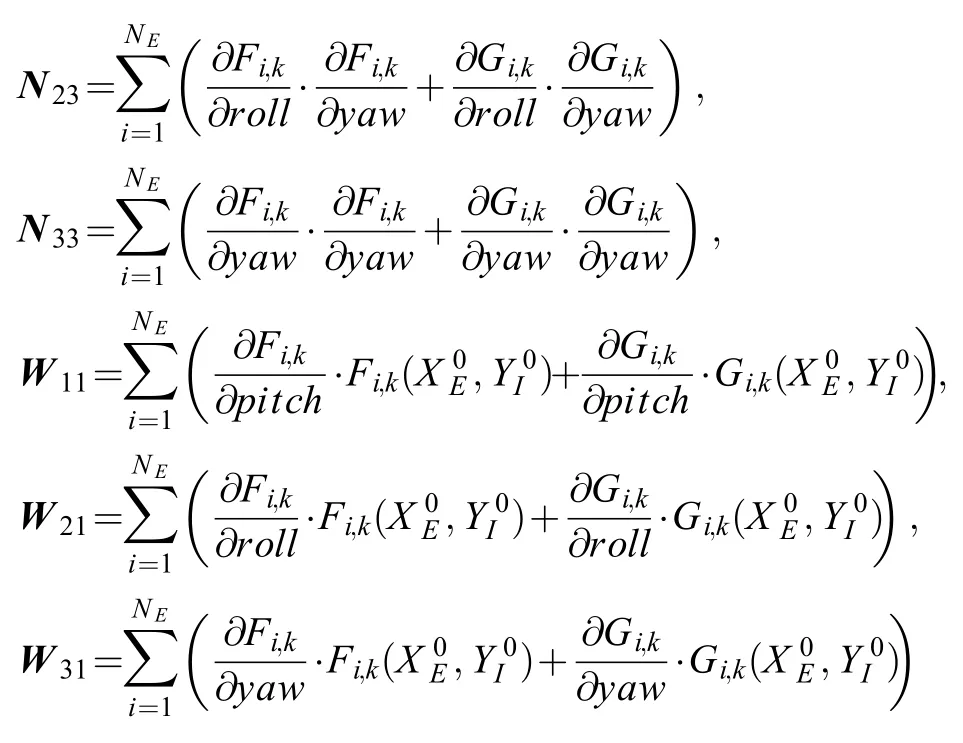
于是，式（17）可改写为

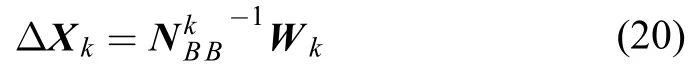
根据式（18）～（20）可知，采用逐行法化最小二乘的方法，每次迭代中只需计算共9个参数的值，分别开辟3 × 3和3 × 1的数组，即可计算出第k次迭代获得的外定标参数的改正数ΔXk。

每次迭代后，将外定标参数的初始值XE0加上计算出的改正数ΔXk，作为下一次迭代的初始值，如式（21）所示。重复此迭代过程，直至，为给定的阈值。

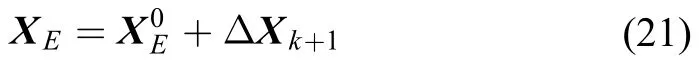
2.2.2用逐行法化最小二乘的方法进行内定标

在外定标之后，我们假设更新的外定标参数XE是真值，来对内定标参数YI进行定标。在内定标中，我们假设NI是每次迭代中参考恒星的数目。

把更新的XE带入公式（15），得到

其中

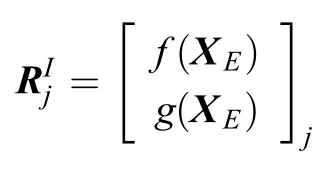
Y是待估计的内定标参数，RjI是根据当前的外定标参数XE计算出来的相机坐标系下第j颗参考恒星的矢量。

由于公式（22）为线性方程，可以用最小二乘法直接计算出Y。

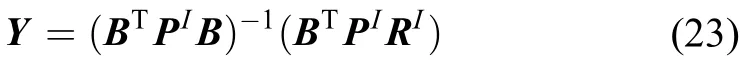
为了在增加参考恒星的数目的同时不增加计算内存的负担，同样采用逐行法化最小二乘的方法进行内定标。假设NBB=BTB，W=BTRI，则有

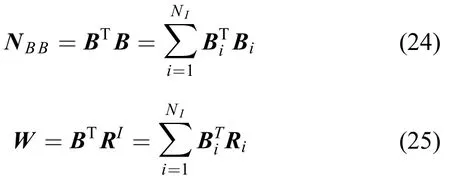
同样，采用逐行法化最小二乘的方法，只需分别开辟20 × 20和20 × 1的数组，即可计算出内定标参数的值。

2.3精度评价

由内外定标参数计算得到参考恒星的惯性矢量的精度，可以用于估计导航敏感器在轨几何定标的精度。因此，计算得到的参考恒星惯性矢量与真实矢量之间的偏差统计量可以作为导航敏感器在轨几何定标精度的评价指标。

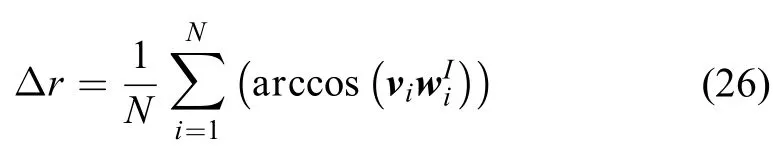
其中：N是参考恒星的数量；vi是由式（7）计算得到的真实的惯性矢量，wiI是由式（13）计算的惯性矢量。

3　实验分析

为了验证本文方法的有效性，本文设计了两个仿真实验。实验一用于测试所提方法流程的整体性能与指向角模型在描述与补偿导航敏感器内部畸变方面的有效性；实验二用于测试在拍摄导航目标源之前，基于已经精确标定的内定标参数，对易变的外定标参数进行重新标定的性能。

由于目前真实的导航敏感器在轨成像的图像尚未能获得，因此本文利用式（3）～（6）模拟导航敏感器的成像模型与成像误差，真实的相机参数与初始的相机参数如表2所示。导航敏感器的内部参数根据深度撞击号任务的中分辨率导航敏感器设置，其视场角约为10 mrad，焦平面大小为512 × 512，像素大小是21 × 21 μm。因此，一个像素的角分辨率约为4′。我们采用式（3）～（5）中的严格物理模型来仿真内部畸变以及评价定标精度，利用式（11）中的指向角模型来检校内部畸变。利用第谷2星表［16］中视星等高于12的约250万颗恒星作为定标的参考恒星数据库。利用真实的相机参数、安装角和恒星数据库，参考恒星在导航敏感器视场中的位置可以根据确定的姿态指向而进行仿真。

表2　初始的与真实的内外相机参数Table 2　The initial and true camera parameters

星点质心提取与姿态量测的噪声是主要的随机误差源，在模拟仿真的时候应该进行考虑。因此在用于定标解算的参考恒星坐标中加入均值为0、标准差为0.3个像素的随机误差；在姿控系统模拟测量姿态时，加入均值为0、标准差为3′的随机误差。为了评价定标的精度，本文模拟了另外100张没有星点提取与姿态量测随机误差的星图，利用定标解算的内部与外部参数计算参考恒星的惯性矢量的偏差。

3.1试验一

由于初始的相机参数与真实的相机参数存在一定的偏差，因此，相同的像素通过内部与外部参数的计算会得到完全不同的惯性指向。因此，需要通过在轨定标，使得各个像素获得高精度的惯性指向。本文通过设置初始的姿态以及固定的指向变换角速率，来模拟参考恒星在焦平面中的像平面坐标。为了保证各星图中的参考恒星尽量均匀地分布在像平面内，设置的角速率尽量不要太小，从而使姿态指向有着明显的改变。

为了评价本文提出的二维指向角模型在补偿相机内部畸变的有效性，本文假设外定标参数是已知的真实值，仅存在内部畸变需要标定，如图4所示。图4（b）显示，通过内定标，焦平面中各像素中最大的指向偏差在0.2′以内，也就是说，通过高精度的内定标，各像素的指向精度可以保证在0.05 pix以内。图4（c）显示，利于本文提出的逐行法化最小二乘估计定标参数，其精度随着参与解算的星图的数量增加而显著提高。

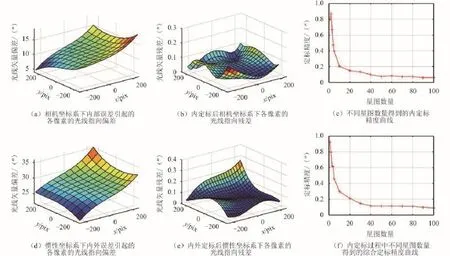
图4　实验一结果图Fig.4　The result map of experiment 1

为了验证本文所提出的先外定标，然后内定标的定标方法的整体效果，假设外定标参数与内定标参数都为待定参数，对导航敏感器进行外定标与内定标，所求的定标系数如表3所示。在外定标过程中，可见定标结果与真实值之间存在明显的偏差，这是由于外定标参数补偿了部分内部畸变，从而使其所确定的并不是真实的相机坐标系，而是广义的相机坐标系。基于广义坐标系所确定的内定标参数的精度随着参与估计的星图数量的增加而增加，如图4（f）所示。同时通过外定标与内定标之后的各像素的最大矢量偏差为0.3′，及0.075 pix，如图4（e）所示。因此，本文提出的定标方法可以通过对外定标参数与内定标参数的组合，实现导航敏感器的高精度的定标。

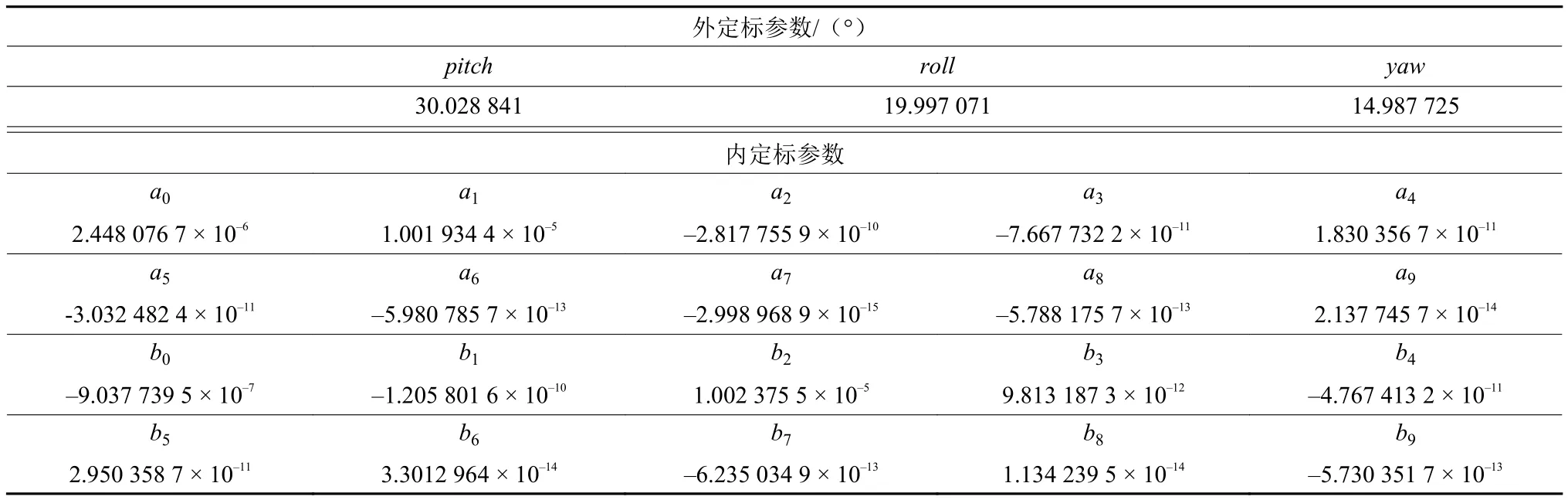
表3　内外定标参数解算结果Table 3　The resolving results of internal and external calibration parameters

3.2实验二

由于外定标参数相对于内定标参数而言更容易受到环境的影响，因此需要相对频繁地进行标定。并且由于外定标参数的变化往往比较剧烈，从而对整体精度的影响就更大，因此，理论上在每次拍摄导航目标源之前，都需要进行外定标参数的重新标定。为了验证基于精确内定标参数的重新外定标方法的有效性，本文设计了真实与初始的外定标参数，如表4所示。内定标参数与初始的外定标参数由实验一中的结果所得。

表4　实验二中外定标参数设置Table 4　The setting of external calibration parameters in experiment 2

如图5（b）所示，所估计的安装矩阵的精度会随着参与解算的星图的数量的增加而增加，尽管会有少量的波动存在。当有100张星图参与解算后，真实的外定标参数与估计的外定标参数之间虽然存在着明显的偏差（如表3所示），但是它们由式（10）决定的安装矩阵同样可以达到很高的精度，如图5（a）所示。由此可见，一个高精度的安装矩阵的精度，并不要求其各个旋转角都要尽可能与真实值接近。图5（a）显示的光线指向的残差曲面与实验一中所得到的残差曲面十分类似，这说明再次的外定标以及消除了绝大部分的外部误差，所剩的残差是由于实验一中的内定标过程中剩余的残差部分。

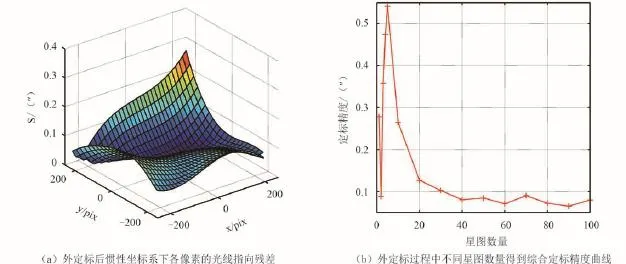
图5　实验二结果图Fig.5　The result map in experiment 2

4　结　论

本文提出了一种分步式导航敏感器在轨几何定标方法，该方法先估计导航敏感器的外部安装参数，然后在外部安装参数决定的广义坐标系下求解内部参数。利用基于逐行法化最小二乘的解算方法，可以有效降低其对星上解算能力的要求，并且可以通过观测更多的星图来提高解算的精度。通过实验可知，导航敏感器焦平面上各个像素的指向可以通过内外定标参数以及姿控系统而高精度恢复。因此，本文所提出的导航敏感器在轨定标方法在精度、有效性、稳定性上都有着优秀的表现，解决了深空探测光学导航中的一项关键问题。

［1］Owen Jr V M. Methods of optical navigation［J］. Spaceflight Mechanics，2011，140：1635-1654.

［2］Rebordão J M. Space optical navigation techniques：an overview［C］// 8th Ibero American Optics Meeting/11th Latin American Meeting on Optics，Lasers，and Applications. ［S. l.］：International Society for Optics and Photonics，2013.

［3］Li S，Lu R K，Zhang L，et al. Image processing algorithms for deepspace autonomous optical navigation［J］. Journal of Navigation，2013，66（04）：605-623.

［4］Christian J A，Lightsey G E. Onboard image-processing algorithm for a spacecraft optical navigation sensor system［J］. Journal of Spacecraft and Rockets，2012，49（2）：337-352.

［5］Kawaguchi J I，Hashimoto T，Misu T，et al. An autonomous optical guidance and navigation around asteroids［J］. Acta Astronautic，1999，44（5）：267-280.

［6］Oberst J，Brinkmann B，Giese B. Geometric calibration of the MICAS CCD sensor on the DS1（Deep Space One）spacecraft：laboratory vs. in-flight data analysis［C］//International Archives of Photogrammetry and Remote Sensing 33.B1；PART 1：221-230（2000）.

［7］Samaan M A，Griffith T，Singla P，et al. Autonomous on-orbit calibration of star trackers［C］// Core Technologies for Space Systems Conference（Communication and Navigation Session），2001.

［8］Hong Y Z，Ren G Q，Liu E H，Non-iterative method for camera calibration［J］. Opt. Express，2015，23（18）：23992-24003.

［9］Lin P D，Sung C K. Comparing two new camera calibration methods with traditional pinhole calibrations［J］. Opt Express，2007，15（6），3012-3022.

［10］Sun T，Xing F，You Z. Optical system error analysis and calibration method of high-accuracy star trackers［J］. Sensors，2013，13（4）：4598-4623.

［11］Wang M，Yang B，Hu F. On-orbit geometric calibration model and its applications for high-resolution optical satellite imagery［J］. Remote Sensing，2014，6（5）：4391-4408.

［12］Wei Q，Liang X，Jiancheng F. A new star identification algorithm based on improved hausdorff distance for star sensors［J］. Aerospace and Electronic Systems，IEEE Transactions on，2013，49（3）：2101-2109.

［13］Zhang P，Zhao Q，Liu J，et al. A brightness-referenced star identification algorithm for aps star trackers［J］. Sensors，2014，14（10）：18498-18514.

［14］Zhou F，Zhao J，Ye T，et al. Fast star centroid extraction algorithm with sub-pixel accuracy based on FPGA［J］. Journal of Real-Time Image Processing，2014（1）：1-10.

［15］Luo L，Xu L，Zhang H. Improved centroid extraction algorithm for autonomous star sensor［J］. Image Processing，IET. 2015，9（10）：901-907.

［16］HEASARC.TYCHO2［EB/OL］.［2015-05-26］. http://heasarc.nasa. gov/W3Browse/all/tycho2.html.

On-orbit Calibration Approach for Optical Navigation Sensor in Deep Space Exploration

CHENG Yufeng，RUN Yi，WANG Mi
（State Key Laboratory of Information Engineering in Surveying，Mapping and Remote Sensing，Wuhan University，Wuhan，430079，China）

Optical navigation sensor is a core instrument in optical autonomous navigation，the accuracy of the direction of light of the navigantion target it acquired will affect the accuracy of autonomous navigation directly. In this paper，a stepwise onorbit geometric calibration approach for optical navigation sensor is designed. Firstly，the external calibration parameters are solved. Then，the internal calibration parameters are sovled in the general camera coordinate system determined by external calibration. Because the computation source and ability is limited in the satellite，in order to using more star images to achieve estimation of calibration parameters with high accuracy，a line-by-line orthogonalization method based on least square is adopted in calibration parameter estimation. The experiments demonstrates that the on-orbit calibration approach proposed in this paper can improve the pointing accuracy of optical navigation sensor，and make it meet the requirements of optical autonomous navigation.

optical navigation sensor；geometric calibration；line-by-line orthogonalization method；least square

V249.32+3

A

2095-7777（2016）03-0228-9

10.15982/j.issn.2095-7777.2016.03.006

程宇峰 （1990- ），男，博士生，主要研究方向：光学卫星数据几何处理。

通信地址：武汉大学测绘遥感信息工程国家重点实验室（430079）E-mail：cyf_whu@126.com

［责任编辑：杨晓燕］

2016-05-26；

2016-07-01

国家重点基础研究发展计划（2014CB744201）