有限推力变轨的月球探测器发射轨道设计

陈新民，周天帅，朱冬阁，王建明

（1. 中国运载火箭技术研究院，北京 100076；2. 北京宇航系统工程研究所，北京 100076）

有限推力变轨的月球探测器发射轨道设计

陈新民1，周天帅2，朱冬阁2，王建明2

（1. 中国运载火箭技术研究院，北京 100076；2. 北京宇航系统工程研究所，北京 100076）

月球探测器的发射是一个多体问题，也是严格的轨道交会问题。发射轨道方案从理论上有很多种形式，但在工程应用中，受到火箭能力、发射场和测控条件等多种因素制约，方案选择限制非常严格。利用现有火箭，采用有限推力从停泊轨道转移发射是最常用的一种发射方式。本文以某典型火箭为例，对采用有限推力变轨方案的奔月轨道设计流程、发射方案、轨道设计方法、精度分析、发射窗口设计进行了详细分析和研究。

有限推力；月球探测；发射轨道设计

引用格式：陈新民，周天帅，朱冬阁，等. 有限推力变轨的月球探测器发射轨道设计［J］. 深空探测学报，2016，3（3）：253-261.

Reference format: Chen X M， Zhou T S，Zhu D G， et al. Launch trajectory design for lunar probes with finite thrust maneuver ［J］. Journal of Deep Space Exploration，2016， 3（3）：253-261.

0　前　言

月球探测器的发射是严格的轨道交会问题，从轨道动力学上讲，是一个多体运动问题。发射月球卫星的轨道方案从理论上有很多种形式，单纯从最优发射轨道设计来讲，采用小推力连续变轨是最为有效的，但从实际工程实施来看，采用有限推力从地球和月球的停泊轨道上转移也是一种经济合理的方式［1］。

连续小推力轨道机动对空间推进装置、远距离、长时间测控控制技术、卫星自主GNC等技术提出了较高的要求，国外已经在这一领域进行了相关的试验，并取得成功。受制于大功率、高比冲、高总冲的空间电推进装置水平限制，国内在连续小推力轨道机动方面尚未应用，空间机动主要采用有限推力变轨方式。本文结合某典型火箭的实际情况，对从圆形过渡轨道进入奔月轨道的有限推力变轨、接近月球的再次机动进入环月轨道的发射轨道设计方法进行了系统研究。该发射轨道设计方法论证的火箭方案参与了我国月球探测工程一期、二期工程论证，相关成果也支撑了后续的月球探测工程论证。

1　转移轨道的设计参数和设计约束

奔月轨道，可以是双曲线轨道、也可以是椭圆轨道，取决于加速段提供进入奔月轨道速度。奔月轨道设计的基本几何关系如图1～图4所示。图1和图2给出了整个奔月轨道相对地球赤道面和月球白道面的关系；由图3可以看出，奔月轨道的升交点赤经、轨道倾角决定了探测器与月交会的空间位置，当飞行器和月球同时到达奔月轨道与白道的交点（赤经和赤纬）时，可以实现飞行器与月球的交会；由图4可以看出，奔月轨道的轨道形状和近地点幅角，决定了从近地点到与月球交会的飞行时间。

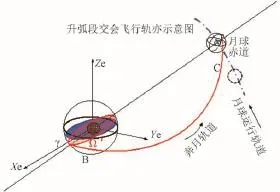
图1　近地变轨进入奔月轨道的方式的飞行轨迹示意图Fig.1　Sketch map of changing orbit from the perigee to earth-lunar transfer trajectory

1.1设计参数

根据以上分析，奔月轨道的主要设计参数为：

1）奔月轨道的升交点赤经；

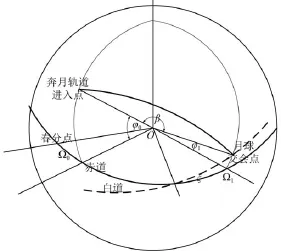
图2　奔月轨道的几何关系示意图Fig.2　Sketch map of earth-lunar transfer trajectory geometry relation

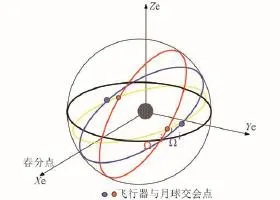
图3　不同的轨道倾角和升交点经度决定了奔月轨道与白道的交点Fig.3　Different Inclination and Longitude of ascending node decide node of earth-lunar transfer trajectory and Moon's orbit

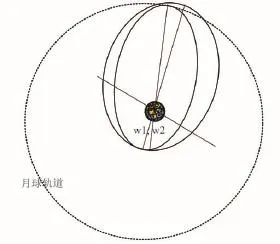
图4　调整轨道形状和近地点幅角可以调整从近地点出发至与月球交会时间Fig.4　Adjusting trajectory shape and perigee argument change transfer time

2）奔月轨道轨道倾角；

3）奔月轨道的轨道形状（半长轴和偏心率）和近地点幅角。

要实现飞行器与月球的交会，轨道设计是非常严格的。在轨道倾角确定的情况下，升交点赤经由进入奔月轨道的时间决定，可以通过调整加速段的起始工作时间来实现。

奔月轨道设计流程图如图5所示。

轨道设计的相对位置关系和设计约束确定后，可以采用迭代制导的轨道设计方法，通过基于单纯形的牛顿迭代法求解。

图5　奔月轨道设计流程图Fig.5　Design flow chart of earth-lunar transfer trajectory

1.2设计约束

1）运载火箭上升段约束

运载火箭上升段约束具体包括运载能力、滑行时间、射向（以及末级偏航程度）。具体表现为星箭分离点轨道倾角、近地点幅角、升交点经度、真近点角等分布在一个相对固定的区间。

2） 国内测控台站约束

为保证国内测控台站对飞行器轨道机动弧段进行测控，需要对飞行器从起飞到月球的飞行时间加以限制，大致为一天半、两天半、三天半、四天半、五天半……，此时可保证飞行器轨道机动弧段测量设备有必要的测量时间和测量仰角要求。从飞行可靠性、能源消耗、测量、控制角度出发，希望尽量缩短飞行时间。但是，从地球停泊轨道到月球轨道的最佳转移（霍曼转移）轨道飞行时间在5天左右，飞行时间过短，将对火箭的运载能力和轨道机动能力提出过高的要求。

3）交会时月球运动方向

在月球围绕地球运行一周的时间内，奔月飞行器与月球实现交会，可以有两个发射期，降交发射期和升交发射期。

4）交会时飞行器所处轨道弧段

为了调整飞行器到达月球的时间，可以选择飞行器在到达远地点前的升弧段到达月球，实现与月球交会，也可以选择飞行器在经过远地点后的降弧段到达月球，实现与月球交会。相应的轨道分别称为升弧段交会轨道和降弧段交会轨道。

5）近月点所处位置

发射月球极轨卫星，奔月轨道可以瞄准月球北极上空，也可以瞄准月球南极上空。当地面测控站位于北半球时，北极近月点奔月轨道测控条件（仰角、斜距、遮蔽角）略优于南极近月点奔月轨道。但由于月球直径仅为地月距离的1%左右，所以两者差别并不大。

1.3转移轨道的基本类型

入轨点约束通常选为近月点，即近月点高度、近月轨道倾角。

在近地点高度、射向和滑行时间给定后，在DX-II坐标系下的轨道倾角、升交点经度、近点幅角、星箭分离点的真近点角也基本随之确定。

对给定的星箭分离点历元、转移时间、近地点高度、近地点轨道倾角、星箭分离点的真近点角以及近月点高度和轨道倾角，存在4条不同的发射轨道［2］。这4条轨道对应着探测器位于近地端和近月端变轨时刻不同的升降轨情况，可以用z方向速度的方向（+为升轨，-为降轨）作为判断依据，也可以由探测器在转移轨道入轨时刻或者环月轨道入轨时刻速度与所在位置子午圈的夹角，即速度射向角AZ来判断，其中AZ＞90°、AZ＜90°分别对应的是降轨和升轨的情况。

设计计算过程中，轨道型号Ⅰ～Ⅳ分别对应降降、降升、升降、升升4种类型，前者对应近地端转移轨道入轨时刻的情况，后者对应近月端环月轨道入轨时刻的情况，如图6所示。在本项目中，由于射向角大于90°，因此近地端是降轨出发，对应Ⅰ型和Ⅱ型发射轨道。

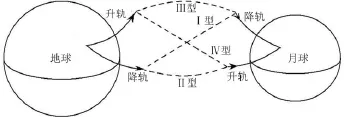
图6　4种类型的转移轨道示意图Fig.6　Sketch map of four styles transfer trajectory

2　地月转移轨道设计［3-5］

微分改正算法是轨道设计中常用的算法。即通过不断的数值迭代来改进轨道初始值，从而将本来不满足约束条件的轨道逐渐改进为满足约束条件的轨道。描述月球探测器的运动方程为

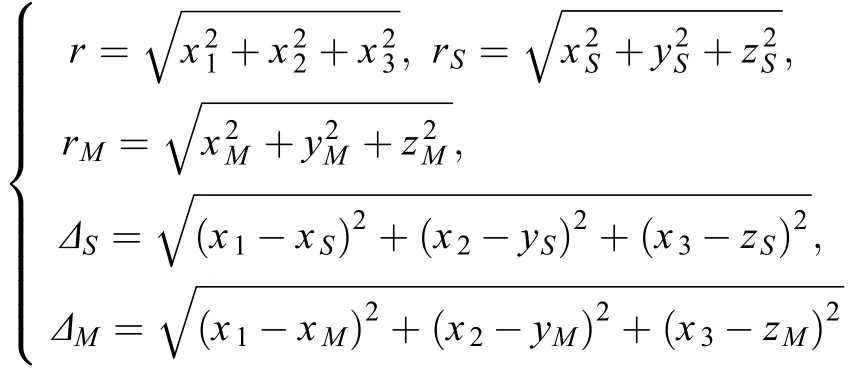
式（1）决定了t0时刻从初始状态量X0出发的一条轨道，记为

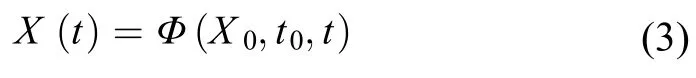
如果对初始状态量X0有约束，记约束的个数为m2，则约束可记为

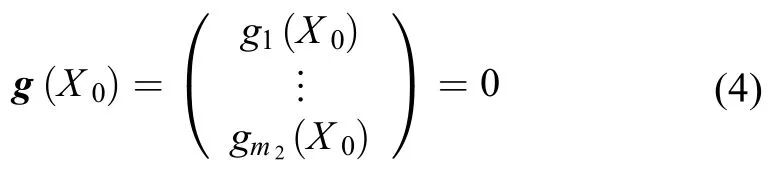
对本项目所需研究的问题，由于研究对象为发射轨道，因此初始状态量为星箭分离点的状态量（即地心天球坐标系下的位置和速度），终了点为近月点。初始状态量的约束可记为（即式（4）的具体形式）

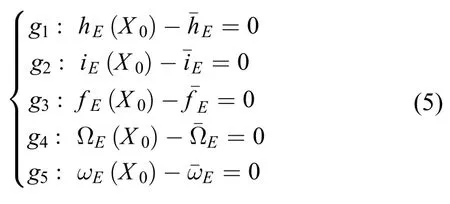
式（5）中每式的第一项表示这些量作为状态量X0的函数，可由二体问题的星历计算得到，而第二项表示预先设定的值。事实上，由于预先设定的值是在DX-Ⅱ坐标系中给出，因此星历计算应在DX-Ⅱ坐标系中给出，记DX-Ⅱ坐标系中星箭分离点的状态量为Y0，则如下转换关系成立

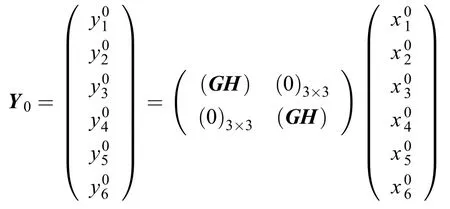
其中：（GH）为地心天球坐标系下的矢量转为DX-Ⅱ坐标系下的矢量的转换矩阵。

假设对终了状态量X有约束，记约束的个数为m1，则约束可记为

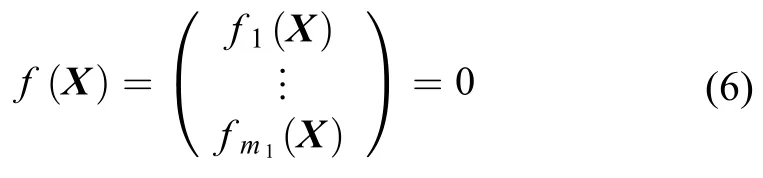
式（6）的具体形式，即终了状态量的约束为

由于X实际是X0的函数，因此式（7）实际是关于X0的方程。需要注意的是，实际计算时用到的不是地心天球坐标系下的状态量X，而是月心J2000平赤道坐标系下的状态量Z，两者间的转换关系为

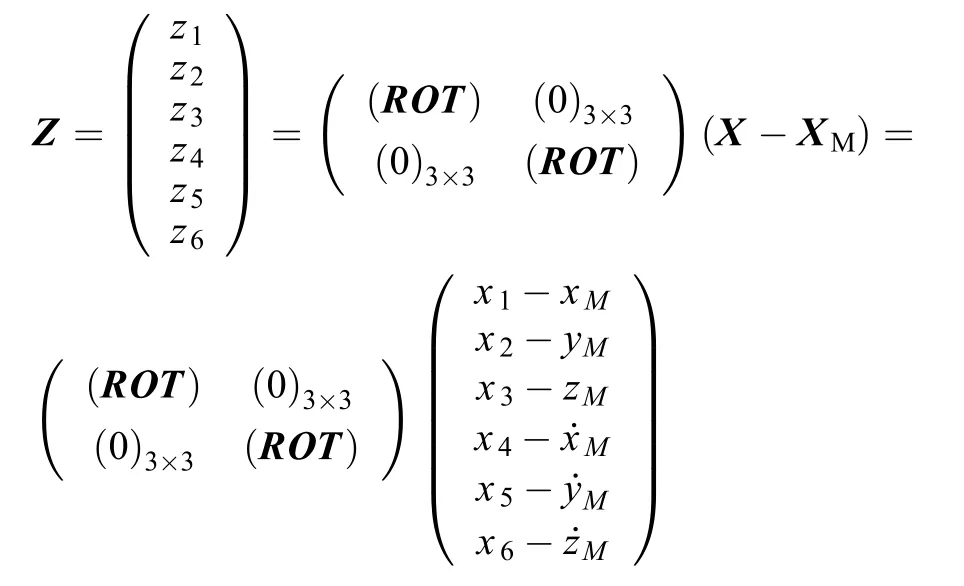
其中：XM为月球在地心天球坐标系下的位置和速度矢量。矩阵（ROT）为月心天球坐标系到J2000月心平赤道坐标系的转换矩阵。

对固定的星箭分离点历元及转移时间而言，实际的可调变量仅有X06个分量，而约束条件却达8个，因此通常情况下此问题不可解。我们解决此问题的方案是选取式（5）的前三式和式（7）作为约束条件，而通过调整不同历元（实际上也可调整转移时间）来同时达到式（5）后两式的要求。这样寻找出来的历元即为发射窗口。

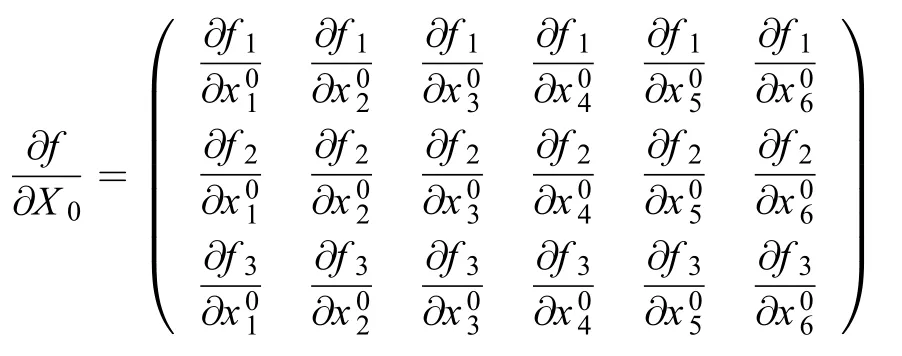
以第一列元素的计算为例

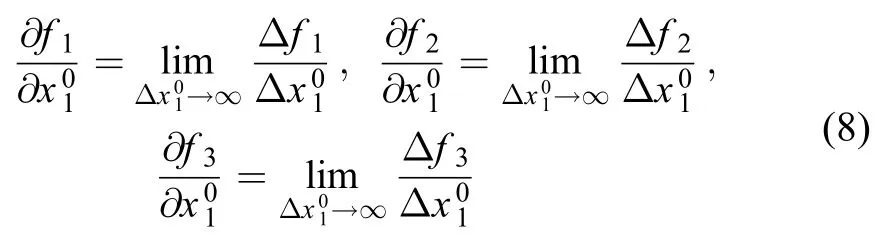
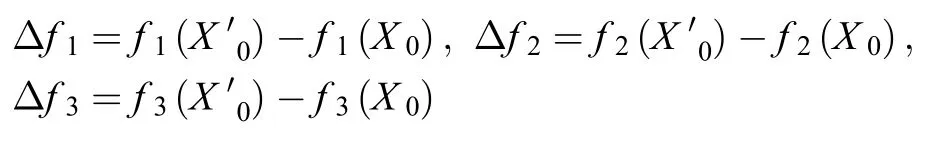
将之代入到式（8）即可得到第一列元素，其他列元素的计算相同。显然，应尽可能小，但不可以太小，无量纲时通常选为10-6～10-7较为合适。

3　某三级火箭+上面级地月转移轨道发射方案

3.1基本思路

本方案基本思路如图7所示。

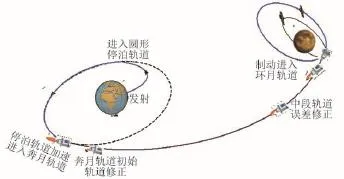
图7　某三级火箭发射月球卫星的轨道方案Fig.7　Trajectory project of three-stage Rocket launching lunar probe

某三级分离前的工作与发射GTO轨道的飞行情况基本一致，火箭一、二、三级一次工作进入200 km的圆形过渡轨道，滑行一定的时间后，三级二次工作将上面级和卫星组合体送入奔月轨道。

采用霍曼变轨，奔月轨道的近地点高度在200 km左右，通过调节三级二次的工作时间来调节远地点高度，通过调节滑行时间和三级二次工作的俯仰程序角，调节奔月轨道的近地点幅角。

3.2典型轨道

3.2.1奔月轨道的初步分析

奔月轨道的近地点高度固定为200 km，奔月轨道的设计主要通过调整奔月轨道的轨道倾角、近地点幅角、远地点高度、进入奔月轨道的时间等来实现。

火箭三级具有侧向机动能力，通过调整侧向偏航程序来调整奔月轨道的轨道倾角，根据运载能力需求调整轨道倾角变化。奔月轨道的近地点幅角变化范围在147.40～199.19°之间，远地点高度通过调整奔月轨道的速度实现。

下面给出典型的飞行轨道来说明情况。

3.2.2奔月轨道

根据第2部分地月转移轨道设计方法，式（5）初始约束取值

式（7）近月点约束取值

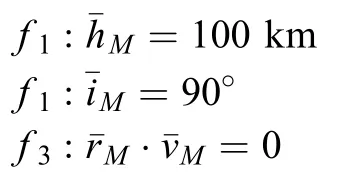
经微分修正法计算，获得典型地月转移轨道数据如表1所示。

发射时间：（北京时间）2003年4月11日08时23分32.7秒，4天半奔月轨道；

发射场：西昌发射中心，104°射向；

各级箭体落区与发射GTO保持一致。

主要特征点参数如表2、3所示，飞行时序如图8所示，测站情况如图9所示，星下轨迹如图10所示。

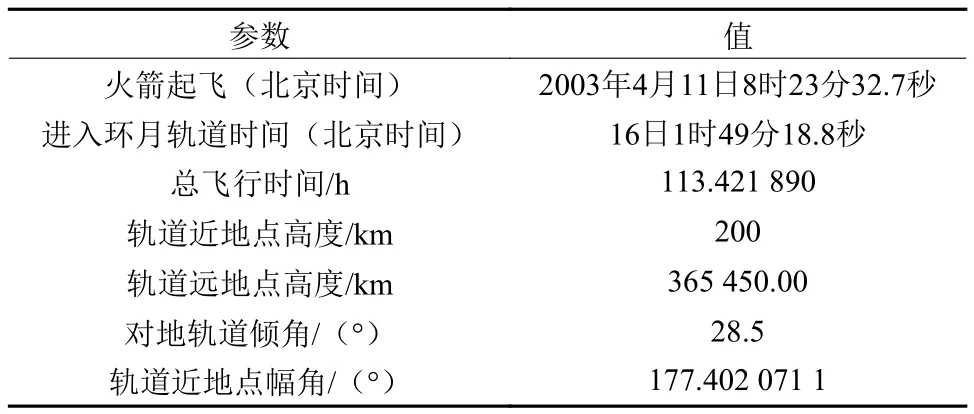
表1　典型地月转移轨道Table 1　Characteristic Earth-Moon transfer trajectory parameters

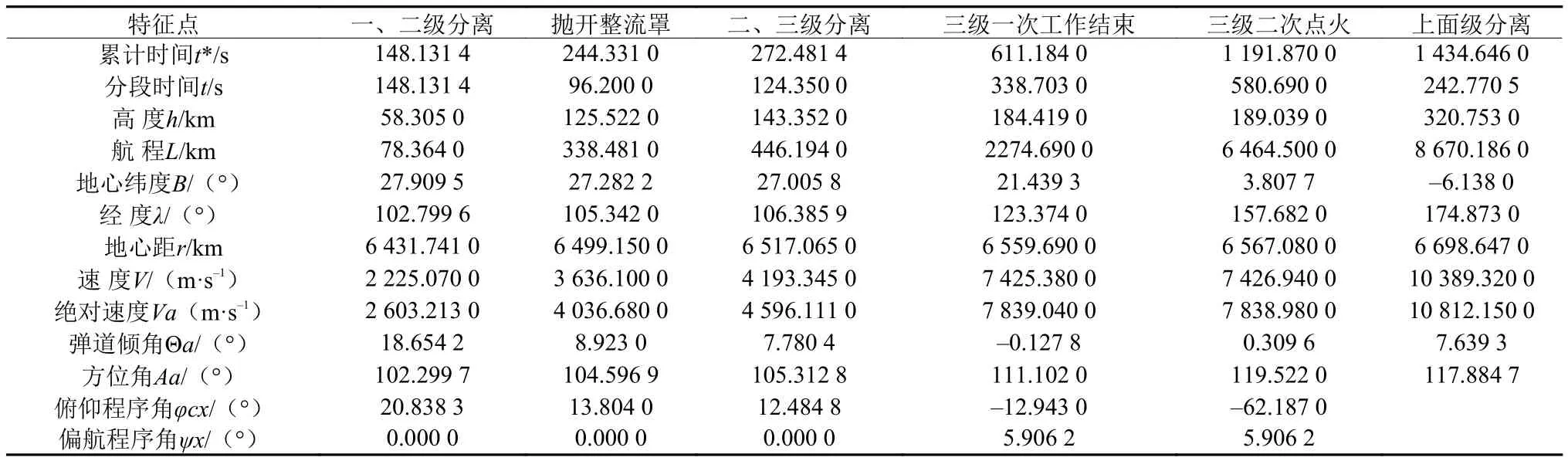
表2　火箭发射轨道主要特征点参数Table 2　Characteristic trajectory parameters of rocket

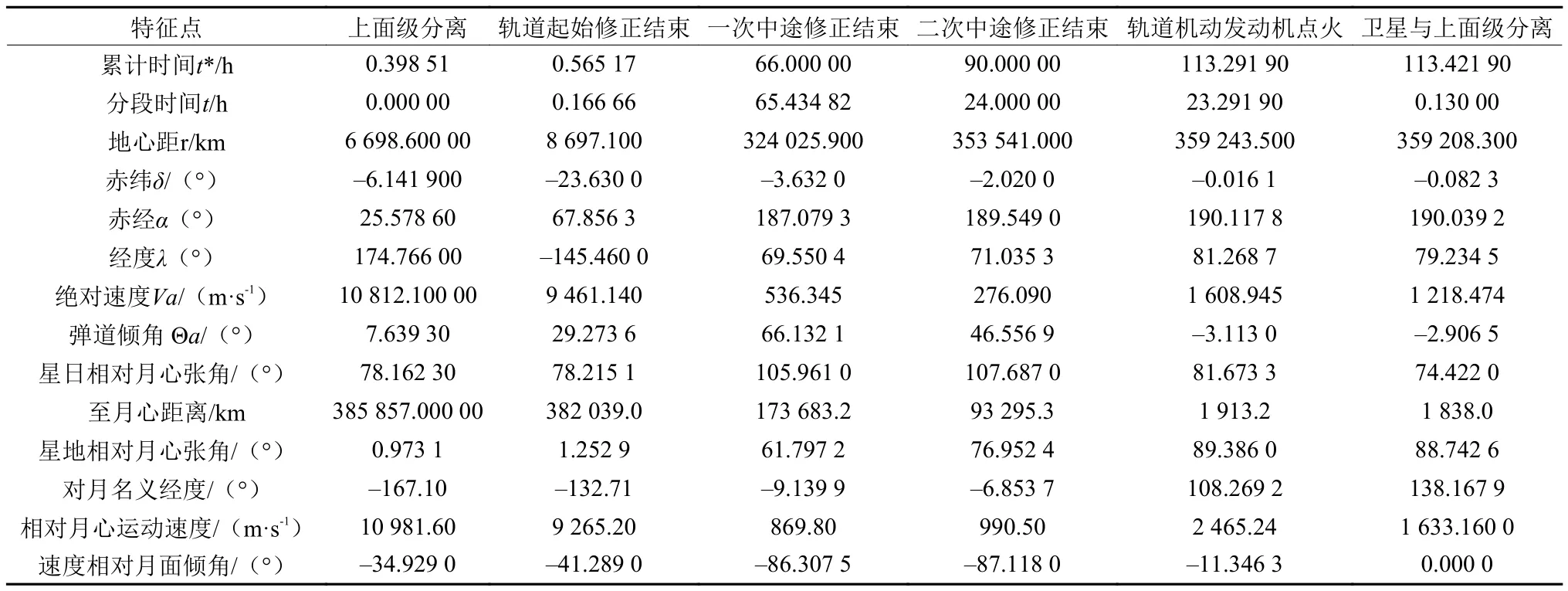
表3　上面级分离后奔月轨道主要特征点参数Table 3　Characteristic trajectory parameter safter upper-stage separation

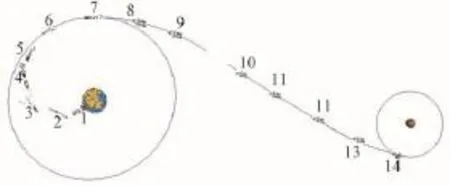
图8　四天半奔月轨道发射的典型时序Fig.8　Typical flight sequence of four and a half days trajectory

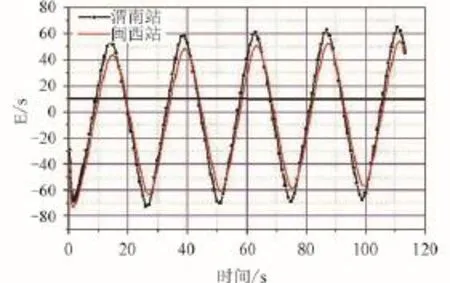
图9　国内两个典型测控站的测量情况Fig.9　Measure case of two typical measure station

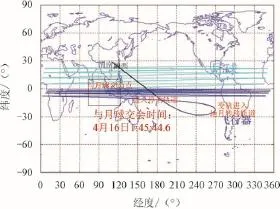
图10　星下点轨迹Fig.10　Track of satellite point subtrack

3.3精度分析

3.3.1关于卫星入轨精度要求

以100 km的极轨为基础，入轨精度偏差为±30 km，轨道倾角为±5°作为分析的依据和对测控的设计要求。当入轨精度要求放宽时，可以放宽相应的测量和控制的精度要求。

3.3.2典型轨道的精度分析

上面的4.5天轨道除进入奔月轨道和进入环月轨道的时刻位于中国上空外，还有4次经过中国上空的机会。精度分配针对进入奔月轨道和中途4次经过中国上空的时段进行分析。主要精度特征点于图11所示。

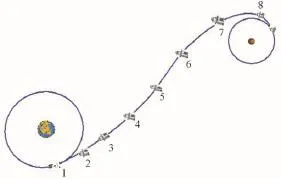
图11　精度分析特征节点Fig.11　Typical events of precision analyse

以下分析基于上面级全自主制导控制方案，以GPS测定上面级运动参数为基础，由上面级自主进行。假设修正结束后的3个方向的速度、位置误差都为0.1 m/s，坐标三分量误差都为200 m。各段的测量和控制精度，对入轨误差的影响分析如下。

1）2段的精度

2段根据GPS的测量信息进行的初始轨道修正，测量信息精度为0.05 m/s，坐标最大误差为30 m，控制精度为速度0.1 m/s，位置200 m，从分析来看，如果不进行中途修正，它引起的环月轨道误差如下：

◆ 轨道倾角误差 8°；

◆ 靠近入轨点的拱点高度误差150 km；

◆ 另一个拱点高度误差30 km。

2）3段的精度

3段仅进行测量，飞行器速度最大误差为0.05 m/s，坐标最大误差为30 m，采用地面注入的数据对飞行器轨道进行中途修正和末端机动控制，除了GPS测量外，不再对飞行器的运动参数（包括对月运动参数）进行任何测量。根据初步计算，卫星进入环月轨道的最大误差如下：

◆ 靠近月球入轨点的拱点高度误差55 km；

◆ 另一个拱点高度误差12 km；

◆ 轨道倾角误差3°。

3）其他各段的精度

如果还需要提高精度，必须依靠地面更高精度的测量信息，如果要将最终卫星的轨道高度控制在30 km的量级，对于4.5 d的奔月轨道，不同时间中途修正，允许的最终修正结束后的速度和位置误差和测量精度要求如下：

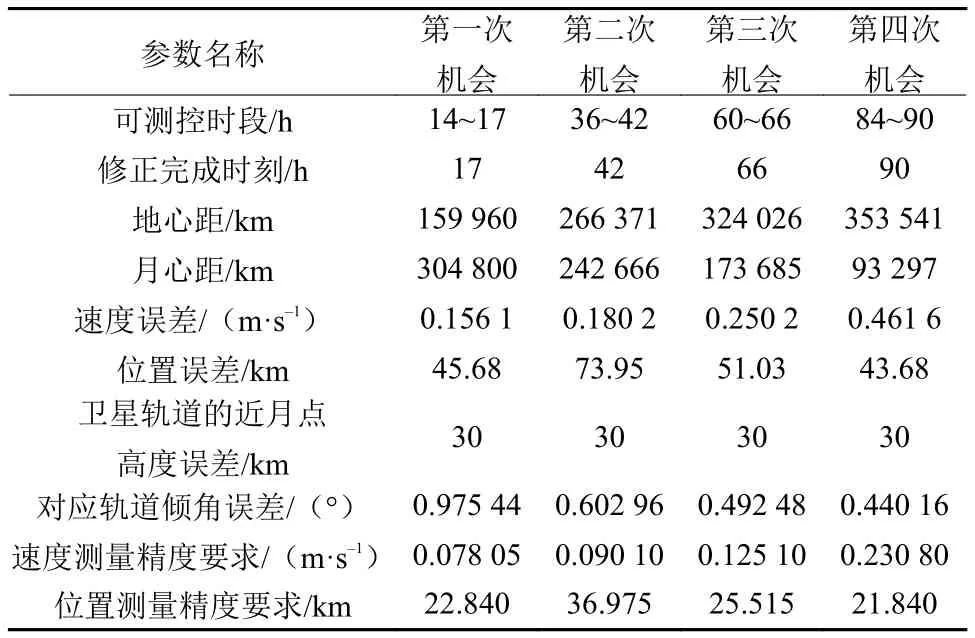
表4　允许修正后的速度和位置误差和测量精度要求Table 4　Velocity and position error and measure precision requirement after correction

3.4发射窗口分析［6］

严格的发射窗口受到航区、测控、太阳光照、月球遮挡等多种约束限制，发射窗口的选择是一个复杂系统的综合决策问题，在任务要求和基本的约束明确后，可以用系统工程的方法分析各种约束条件的合理性，协调相互矛盾的因素，建立有关条件与发射时间之间的数学关系，进行发射窗口的计算。

这里仅基于运载火箭的性能，对轨道约束决定的从停泊轨道向奔月轨道变轨转移的时间段，即火箭允许发射的基本时间段进行分析。

月球围绕地球运动的轨道接近圆形轨道，轨道相对地球赤道的倾角以18.6年为周期在18°19′～28°35′之间变化，对于每个月而言，轨道倾角范围变化很小，可以认为基本是确定的。月球轨道在地球上星下点轨迹的变化如图12所示。

图12　月球轨道在地球上星下点轨迹的变化范围Fig.12　Change range of moon's orbit point subtrack

月球轨道的轨道倾角决定了月球相对地球的视赤纬的最大范围A，随着月球绕地球的周期运转，月球相对地球的视赤纬在这个范围内变化（-A～+A）。

要与月球交会，奔月轨道远地点所能到达的纬度范围必须在月球轨道运行的纬度范围内。奔月轨道的轨道倾角和奔月轨道近地点幅角来调整奔月轨道远地点纬度。在圆形过渡轨道上，可以通过调节滑行时间（来调整进入奔月轨道的时间），来保证奔月轨道的远地点视经度与月球视赤经一致。只要奔月轨道远地点的纬度范围小于月球相对地球的视赤纬的范围，则每天都有一次发射机会。

对于每天的发射来说，可以通过调整进入奔月轨道的远地点高度、奔月轨道的近地点幅角和轨道倾角设计几种奔月轨道，调整能力取决于运载火箭的运载能力和停泊轨道上滑行时间的调节范围。

当奔月轨道的远地点纬度调节范围在当月月球轨道倾角范围以内，则发射机会受到限制。某三级火箭发射奔月轨道的运载能力及轨道调节范围如表5所示。

考虑月球轨道倾角周期性变化，最小为18.5°左右，最大为28.5°左右，月球每27.3天左右运行一周，其纬度变化范围在轨道倾角的范围以内。

以奔月轨道倾角36°为例，根据月球一个运行周期内不同月球轨道倾角下星下点轨迹纬度变化范围与奔月轨道远地点纬度关系，确定发射窗口，如图13和图14所示。两条水平线范围内为可实现发射窗口。根据两个图形可以看出，月球轨道倾角小时，每个月可以发射的机会要多一些，根据火箭奔月轨道远地点纬度调节范围情况可以看出，当月球轨道倾角为18.5°时，每个月有15天左右的发射机会，当月球轨道倾角为28.5°时，每个月有10天左右的发射机会。

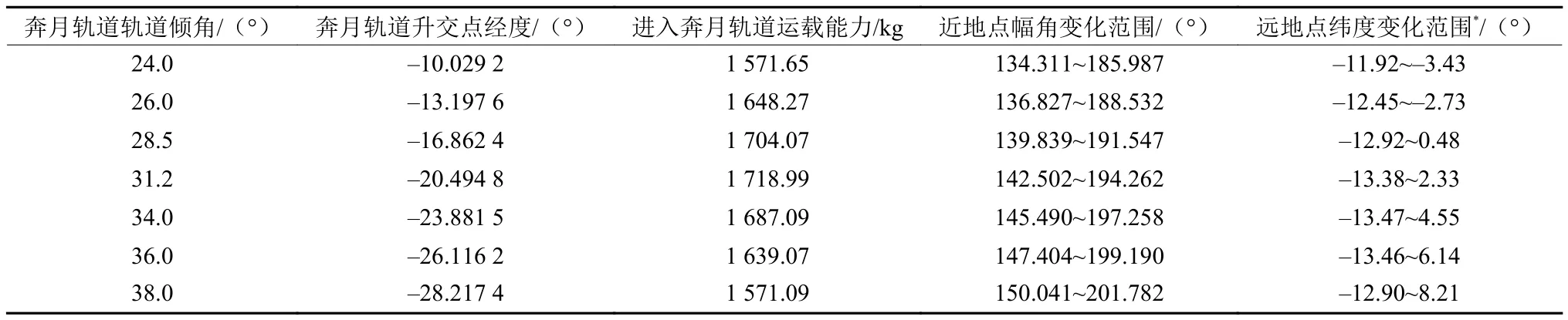
表5　某三级火箭火箭发射奔月轨道运载能力及主要轨道参数Table 5　Earth-Moon transfer trajectory capcity and mostly trajectory parameters of three-stage rocket

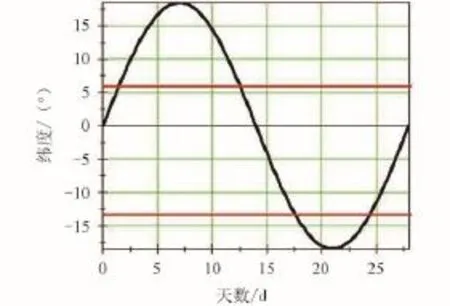
图13　月球轨道倾角18°时发射窗口Fig.13　Launch windows when 18° moon's orbit Inclination

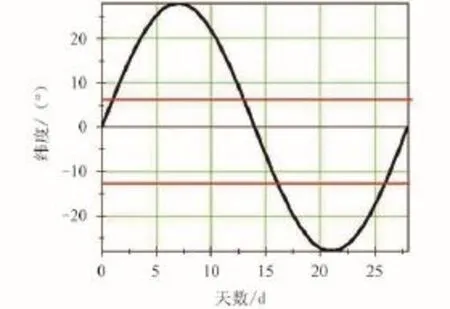
图14　月球轨道倾角28°时发射窗口Fig.14　Launch windows when 28° moon's orbit Inclination

4　结束语

奔月轨道的设计需要考虑运载能力、精度、测控等各方面的设计约束条件，是一个复杂的多体动力学问题。本文通过典型轨道的设计，对采用有限推力变轨方案的奔月轨道设计流程、发射方案、轨道设计方法、精度分析、发射窗口设计等进行了详细介绍，为相关的研究提供参考。

［1］郗晓宁，王威，高玉东. 近地航天器轨道基础［M］. 北京：国防科技大学出版社，2003：268-313. Xi X N，Wang W，Gao Y D. Near-Earth spacecraft orbit foundation［M］. National Defence Science and Technology Press，2003：268-313.

［2］杨维廉. 发射极月卫星的转移轨道研究［J］. 航天器工程，1997，9（3）：23-32. Yang W L. Transfer trajectory research for lunar polar satellite launching［J］. Space Engineering，1997，9（3）：23-32.

［3］崔平远，乔栋，崔祜涛. 深空探测轨道设计与优化［M］. 北京：科学出版社，2014：45-64. Cui P Y，Qiao D，Cui H T. Deep-space exploration orbit design and optimize ［M］. Beijing：Science Press，2014：45-64.

［4］杨嘉墀. 航天器轨道动力学与控制（上） ［M］. 北京：宇航出版社，1995：544-557. Yang J C. Space orbit dynamics and control（up）［M］. Beijing：Space Navigation Press，1995，12：544-557.

［5］褚桂柏，张熇. 月球探测器技术［M］. 北京：中国科学技术出版社，2007：135-149 . Chu G B，Zhang H. Lunar exploration technique［M］. Beijing：China Technology Press，2007：135-149.

［6］黄文德，郗晓宁，王威. 从近地轨道入轨的载人登月发射窗口分析与设计［J］. 天文学进展，2010，9（3）：310-319. Huang W D，Xi X N，Wang W. Launch window analysis and trajectory design for manned landing mission from near-Earth orbit injection to the Moon ［J］. Progress in Astronomy，2010，9（3）：310-319.

通信地址：北京9200信箱1分箱（100076）

电话：（010）88521130

E-mail：chenskyb@sina.com

Launch Trajectory Design for Lunar Probes with Finite Thrust Maneuver

CHEN Xinmin1，ZHOU Tianshuai2，ZHU Dongge2，WANG Jianming2
（1. China Academy of Launch Vehicle Technology，Beijing 100076，China；2. Beijing Institute of Astronautical Systems Engineering，Beijing 100076，China）

To launch a lunar probe is a multi-celestial body problem，and also a strict orbit rendezvous problem. Many launch trajectory plans can be obtained theoretically，but selctions are strictly limited for enginnering applications with many constarints，such as launch capacity，launch site，telemetry and control conditions etc. The most conventional method is to transfer from the parking orbit with finite thrust. This paper takes a typical launch vehicle as an example，the Earth-lunar transfer scheme with constraints are analyzed and studied.

finite thrust；lunar exploration；launch trajectory design

V412.4

A

2095-7777（2016）03-0253-9

10.15982/j.issn.2095-7777.2016.03.009

陈新民（1972- ），男，博士，研究员，主要研究方向：飞行器设计。

［责任编辑：宋宏］

2016-05-18；

2016-06-19