火星探测器捕获段自适应卡尔曼滤波方法

宁晓琳，李卓，黄盼盼，杨雨青，刘刚，房建成

（1. 北京航空航天大学　仪器与光电工程学院，北京 100191；2. 新南威尔士大学　土木与环境工程学院，悉尼 2052）

火星探测器捕获段自适应卡尔曼滤波方法

宁晓琳1，李卓1，黄盼盼2，杨雨青1，刘刚1，房建成1

（1. 北京航空航天大学仪器与光电工程学院，北京 100191；2. 新南威尔士大学土木与环境工程学院，悉尼 2052）

天文导航是一种广泛应用于深空探测任务中的节能、高效的导航方式。基于轨道动力学模型和星光角距的卡尔曼滤波方法已经被成功应用在天文导航系统中。在捕获段由于探测器所处动力学环境复杂，未建模的加速度误差，星历误差等都会造成过程噪声统计特性不完全。针对以上问题，提出一种根据新息和残差序列的变化趋势来调节过程噪声协方差阵的自适应平方根容积卡尔曼的方法（AQSCKF）。该方法先分别利用新息和残差计算调节因子，然后判断新息和残差的变化趋势，当新息和残差的变化趋势一致时，取二者调节因子的均值作为过程噪声方差阵的调节因子，对其进行调节。此外，本文还将该方法与传统的只利用新息或残差在线调节协方差阵的平方根容积卡尔曼滤波（SCKF）方法进行对比，仿真结果表明，在解决由于过程噪声统计特性不能完全已知的问题上，AQSCKF算法不仅能显著提高导航精度，并且具有很好的稳定性。

自适应滤波；天文导航；过程噪声；卡尔曼滤波

引用格式：宁晓琳，李卓，黄盼盼，等. 火星探测器捕获段自适应卡尔曼滤波方法［J］. 深空探测学报，2016，3（3）：237-245.

Reference format: Ning X L，Li Z，Huang P P，et al. An adaptive Kalman filter for Mars spacecraft acquisition phase ［J］. Journal of Deep Space Exploration，2016，3（3）：237-245.

0　引　言

天文导航方法作为一种自主的导航方式，已经被广泛应用在许多深空探测任务中。例如2001年“深空1号”（Deep Space 1）成功飞跃Borrelly彗星［1］，同年“星尘号”成功飞跃wild2彗星［2］，以及2005年“深度撞击号”飞跃Temple1［3］。天文导航的基本原理是利用探测器上安装的天体敏感器观测天体的方位信息，通过星历表获得天体在惯性空间中任意时刻的位置，从而确定探测器在该时刻的位置和姿态信息。在天文导航系统中，由于过程噪声和量测噪声的存在，通常采用最小二乘法［4］或基于轨道动力学方程的卡尔曼滤波方法来减小噪声对导航结果的影响。最小二乘法是天文导航系统常用的一种滤波方法，该方法主要是使得量测量和由状态估计所确定的量测估计的差值的平方和达到最小［2］。卡尔曼滤波算法是一种递推的估计算法，该方法是基于最小方差估计的最优估计方法［5］。在天文导航系统中，由于系统状态和量测方程的非线性特性，经常使用非线性滤波方法来获得较高的导航精度。目前常用的非线性滤波方法主要有扩展卡尔曼滤波（EKF）［6］、无迹卡尔曼滤波（UKF）［7］、容积点卡尔曼滤波（CKF）［8］和平方根容积卡尔曼滤波（SCKF）［9］。其中UKF、CKF以及SCKF是利用采样点来获取状态均值和协方差的滤波方法。与EKF相比，UKF、CKF和SCKF有更好的滤波性能［10-11］。本文采用SCKF来进行仿真分析，与CKF相比，该方法不仅降低了计算复杂度，可以获得更高的滤波效果，并且能有效地避免滤波器的发散，提高滤波的收敛速度和数值稳定性［12］。同EKF、UKF和CKF一样，SCKF依赖于过程噪声和量测噪声的先验信息，但由于捕获段探测器所处的动力学环境复杂，未建模加速度，天体星历误差的存在等都使得无法得到准确的过程噪声统计特性［13］。因此，在初始时刻设置滤波初值时，很难获得准确的过程噪声协方差阵。

针对捕获段探测器天文导航过程噪声统计特性难以精确确定的问题，许多学者已经进行了研究。目前主要是通过自适应滤波的方法来解决该问题，常用的3种自适应滤波方法主要有：在线估计法、多模型估计法（MME）以及在线调节法。在线估计的方法是基于贝叶斯估计、最大似然估计、相关法和协方差匹配等法则直接对过程噪声协方差阵进行估计，该方法虽然计算较为简单，但是滤波精度有限［10-11，13-15］。多模型估计方法是指一些具有不同模型参数的滤波器同时进行滤波，并且通过对每个滤波器的滤波结果进行融合最后得到最优的滤波估计。该方法虽然在导航精度上有了一定的提高，但是由于需要设置多组模型参数逼近真实系统，故其计算较为复杂［16-17］。在线调节的方法引入调节因子在线调节噪声方差阵，其中调节因子的计算方法一般有两种：一种是基于新息的计算方式，另一种是基于残差的计算方式。以上两种方法均是通过计算新息或残差的估计误差方差阵与其对应理论误差方差阵的比值得到。在火星探测器捕获段，由于过程噪声和量测噪声变化是不确定的，而新息受量测噪声的影响较大，残差序列又受到前一时刻的估计值的影响，因此，单独使用新息序列或是残差序列来调节过程噪声方差阵的方法经常会导致过度调节或者是估计精度不高。为了增加噪声方差阵的稳定性，本文提出了一种基于容积卡尔曼滤波算法的新的自适应过程噪声方差阵的滤波方法（AQSCKF）。该方法中，调节因子的值是通过同时判断新息序列和残差序列的变化趋势，进而在二者变化趋势一致时，取二者的均值而得到。此外，本文还通过仿真试验将该算法与传统的SCKF——只利用新息或残差的在线调节方法进行了对比，仿真结果表明AQSCKF可以解决因噪声统计特性不确定所引起的导航精度下降的问题，并且具有很高的稳定性。

1　火星探测器天文导航系统模型

捕获段火星探测器天文导航系统中，系统模型为由轨道动力学模型作为状态模型，恒星星光角距作为量测模型，进而通过滤波算法进行最优估计得到探测器的位置、速度、姿态等信息。

1.1状态模型

当火星探测器处于捕获段时，其轨道动力学模型可以看作圆形限制性四体问题，该方法经常需要考虑在太阳和附近天体中心引力对探测器的作用。则探测器在日心惯性系坐标系下的轨道动力学模型可以表示为

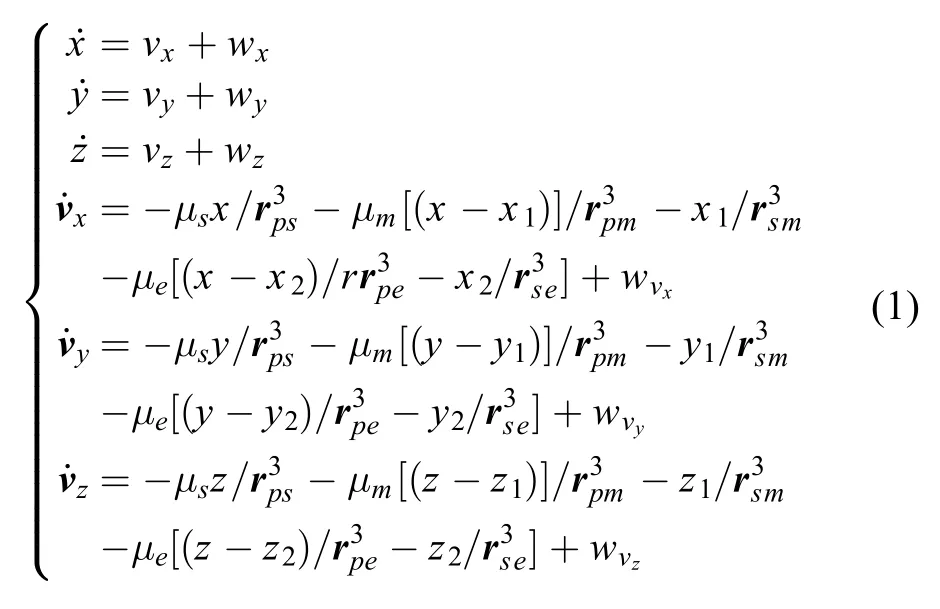
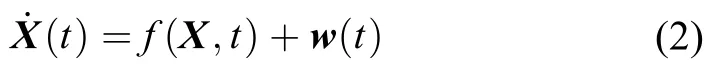
1.2量测模型

火星探测捕获段的天文导航方法通常是以火星及其卫星与恒星之间的星光角距作为量测量。火星、火卫一、火卫二和恒星之间的星光角距的位置关系如图1所示。

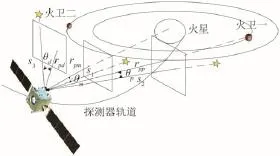
图1　恒星与导航天体间的星光角距Fig.1　Star angles between the stars and the navigation celestial body

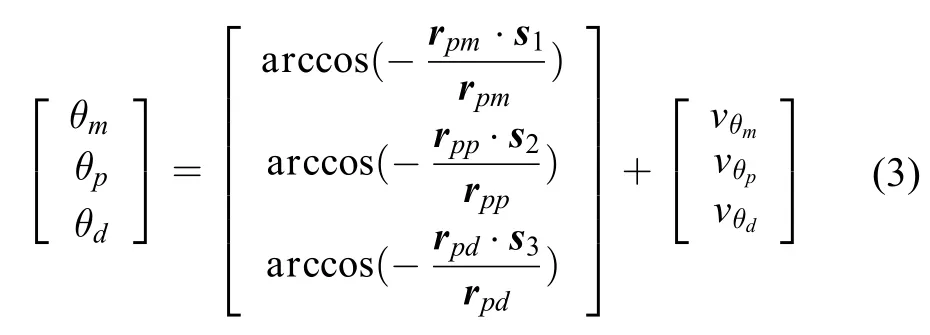
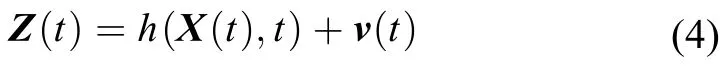
2　AQSCKF算法

本小节中首先给出SCKF算法的简要算法流程，然后给出AQSCKF算法的具体算法流程。

2.1SCKF算法

SCKF是在CKF的基础上，基于平方根滤波的思想提出的一种新的滤波方法。与CKF相比，SCKF不仅降低了计算的复杂度，而且提高了滤波效率，提高了滤波的收敛速度［12］。

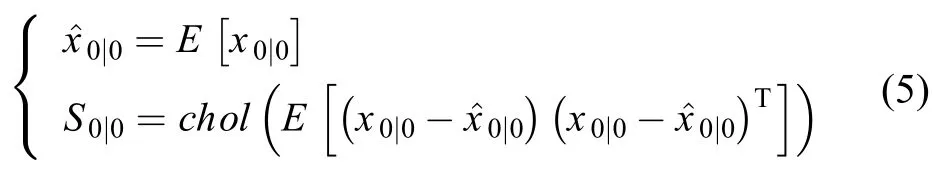
1）时间更新

容积点计算：

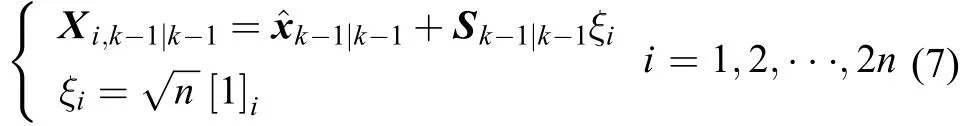
通过非线性状态方程传播的容积点：

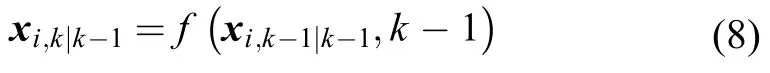
状态估计预测值和一步预测误差方差阵的平方根计算：

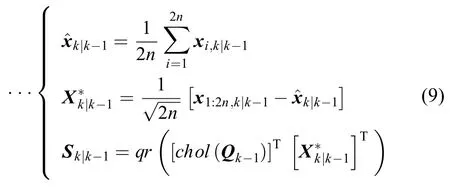
其中：Sk|k-1表示一步预测误差方差阵的平方根；表示矩阵的QR分解。

2）量测更新

容积点计算：

通过非线性量测方程传播后的容积点：

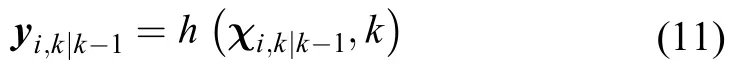
量测预测值，预测误差方差阵平方根和互协方差阵的计算：

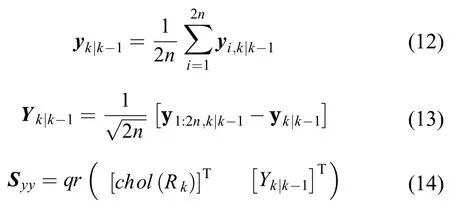
其中：Syy表示预测误差方差阵的平方根；为量测误差方差阵。

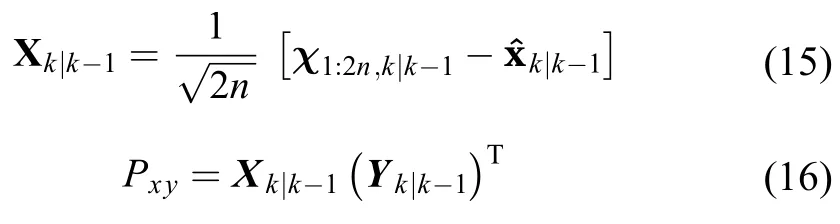
其中：Pxy表示互协方差阵。

增益阵、状态估计值和状态估计误差方差阵的计算

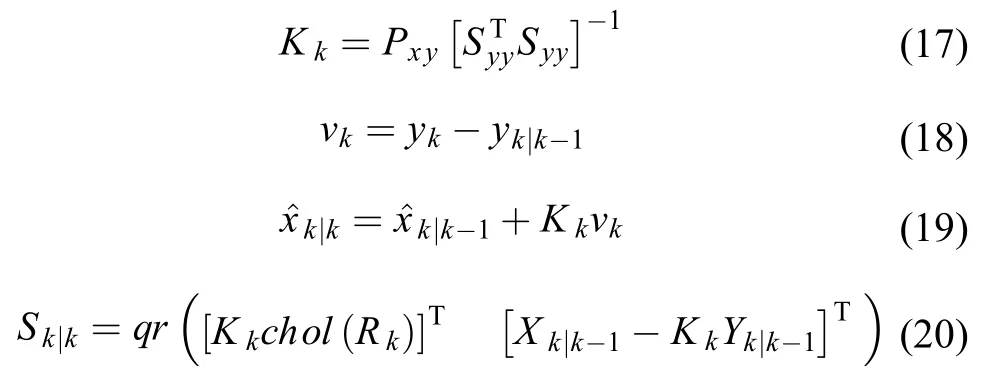
2.2传统调节方法

利用SCKF算法对系统进行滤波时，要求噪声统计特性准确已知，并在滤波过程中保持不变，但在火星探测器捕获段天文导航系统中，过程噪声的统计特性是部分已知，或完全未知的并且随时间变化的。此时，若采用传统的滤波方法将会导致滤波性能变差，甚至发散。故为提高滤波精度和稳定性，并适应过程噪声统计特性时变的特性，应采用自适应Q阵的方法来提高Q阵的稳定性和滤波精度。

通常情况下，自适应调节Q阵是通过引入一个调节因子来对过程噪声统计特性进行在线调节，调节过程如下：

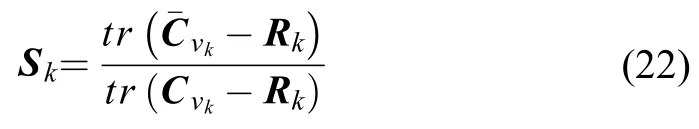
文献［20］给出了另外一种基于残差序列的计算调节因子计算方式，具体过程如下：

2.3AQSCKF

2.3.1自适应调节Q阵的条件

2.3.2调节因子Sk的计算

在AQSCKF算法中，只有在满足调节Q阵的条件下，才对Q阵进行调节，具体调节过程如下：

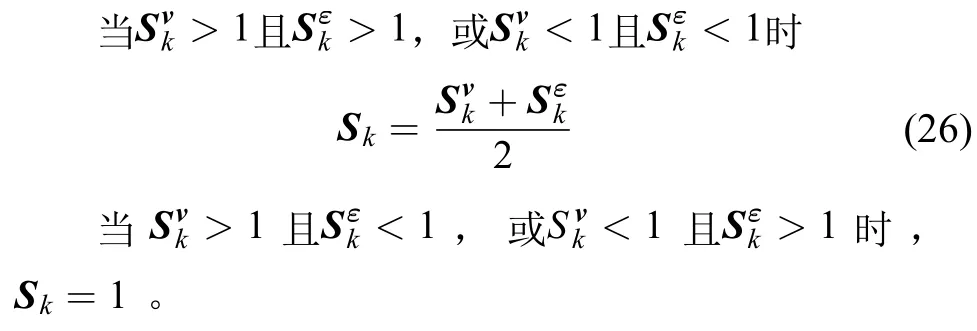
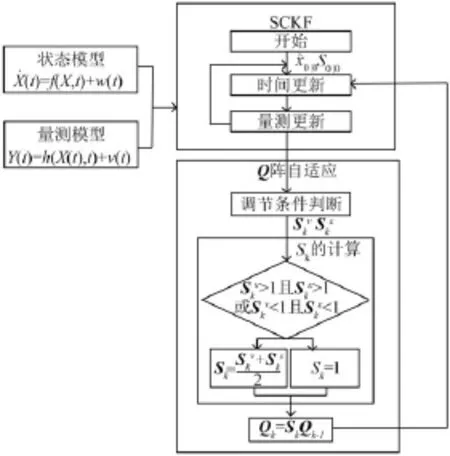
图2　AQSCKF算法计算流程图Fig.2　Diagram of AQSCKF

AQSCKF的具体计算流程如图2所示。

下面给出AQSCKF算法的详细计算过程。

1）时间更新

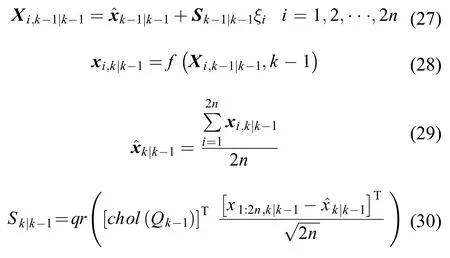
2）量测更新

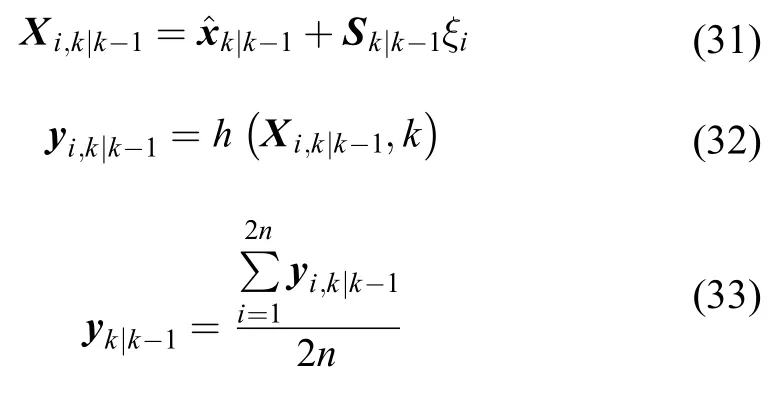
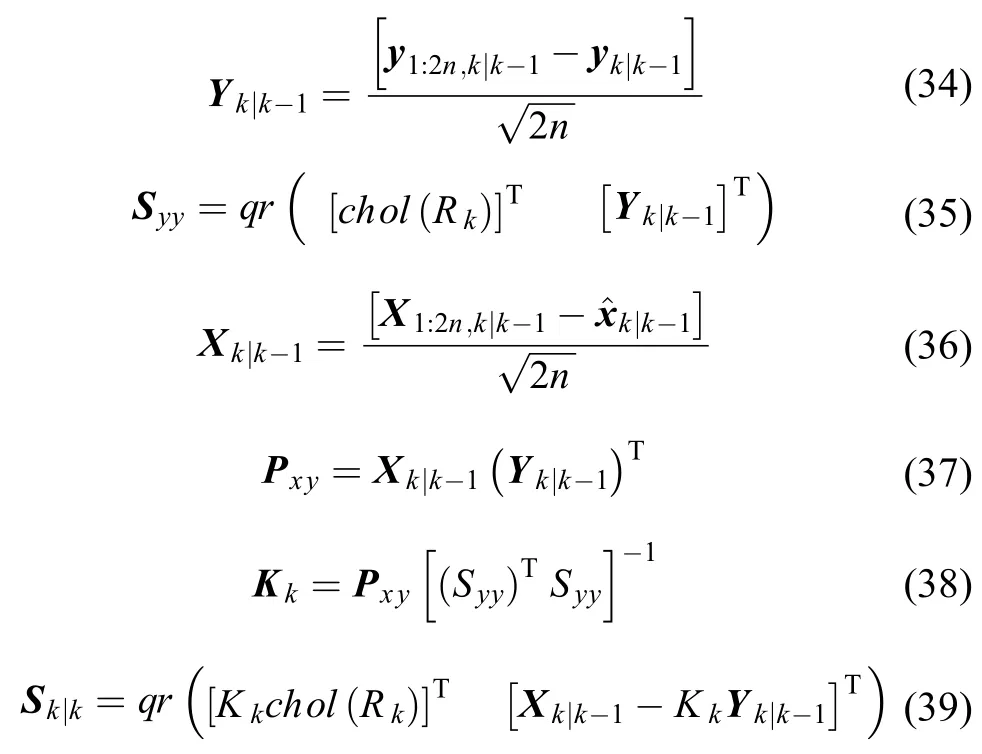
3）自适应Q阵

3　仿真结果及分析

3.1仿真条件

本文所采用的标准轨迹为1997年NASA发射的Pathfinder，其轨道数据由STK直接产生［21］。仿真中所使用探测器的初始轨道参数表1所示。

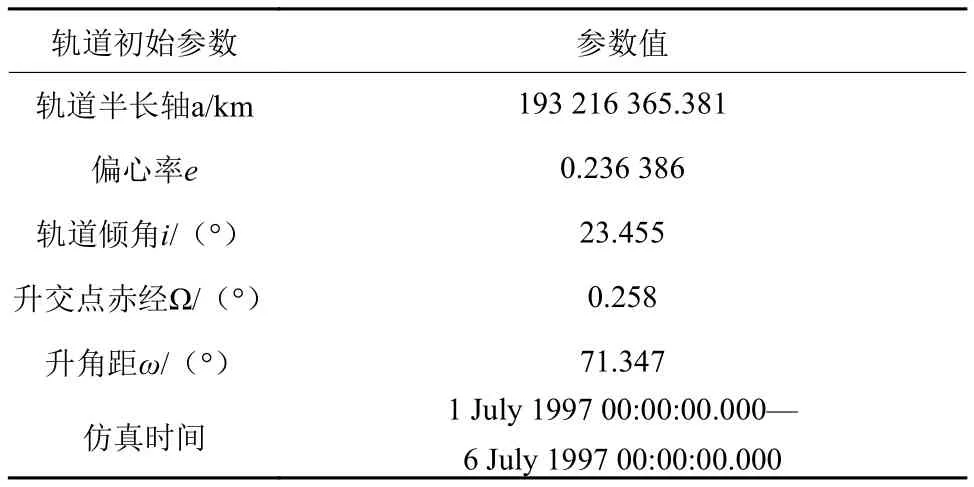
表1　初始时刻轨道参数Table 1　The parameter of initial orbit

仿真中所用探测器，火星、火卫一、火卫二的位置信息也是从STK中利用DE421和SPICE星历产生。火星、火卫一、火卫二在日心黄道惯性坐标系下的轨迹如图3所示。

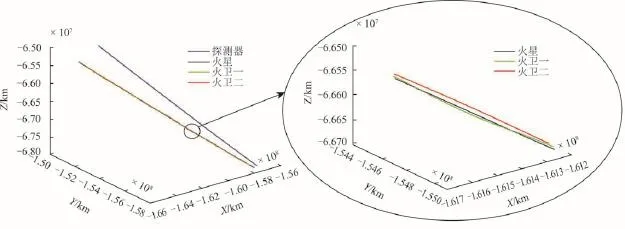
图3　火星，火卫一和火卫二的标准轨迹Fig.3　The ideal trajectories of Mars，Phobos，Deimos and explorer

3.2仿真结果

3.2.1SCKF与AQSCKF的导航结果对比仿真过程中，设过程噪声方差阵Q=q*diag。图4和表2给出了在q分别为0.01，1和100时，SCKF和AQSCKF算法下的导航性能对比。

从仿真结果可以看出，q值大小对于SCKF的滤波结果有很大的影响。当q取值太大时，由于滤波中设置的q值固定，此时认为状态模型精度差，状态估计的精度主要依赖于量测量的精度，从而导致不能有效利用状态模型对状态量进行估计。反之，当q取值太小时，滤波器此时滤波器认为状态模型可靠，从而减小对于量测信息的依赖，进而造成不能有效利用量测信息对状态预测的估计进行修正。导致滤波精度不高，甚至发散。从表2 中的滤波结果可以看出，不论q值如何设定，AQSCKF算法的滤波结果总是稳定在4～6 km的范围内。这是因为不同于SCKF算法，AQSCKF算法同时利用了新息和残差的变化趋势信息在滤波过程中实现了自适应调节Q阵，使得当预设的q值与实际Q阵不符时，该算法能自适应调节Q值大小，直到Q值与实际值相符。

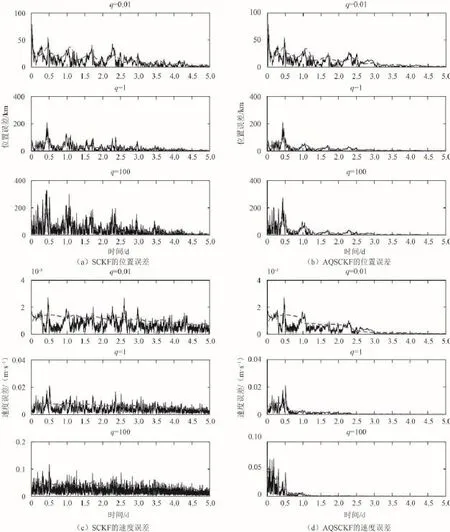
图4　SCKF与AQSCKF导航性能对比Fig.4　The navigation performance of SCKF and AQSCKF

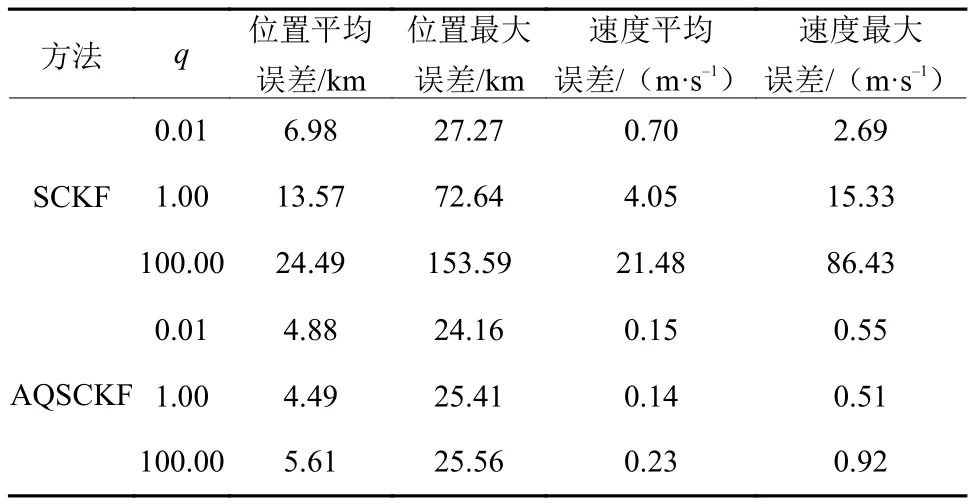
表2　SCKF与AQSCKF导航结果Table 2　Simulation result of SCKF and AQSCKF

3.2.2传统自适应滤波方法与AQSCKF的导航结果对比

传统的自适应调节Q阵是通过引入一个调节因子来对过程噪声统计特性进行再线调节。其中调节因子的计算方法一般分为两种：基于新息序列计算调节因子［19］和基于残差序列计算调节因子［20］。本文中，式（24）给出了基于新息计算调节因子的方式，式（25）给出了基于残差序列计算调节因子的方式。图5和表3给出单独利用基于新息和残差自适应调节Q阵的仿真结果，仿真中，估计窗口值M为200。

图5　基于新息和残差的自适应滤波导航性能Fig.5　The navigation performance of adaptive filter based on innovation and residual

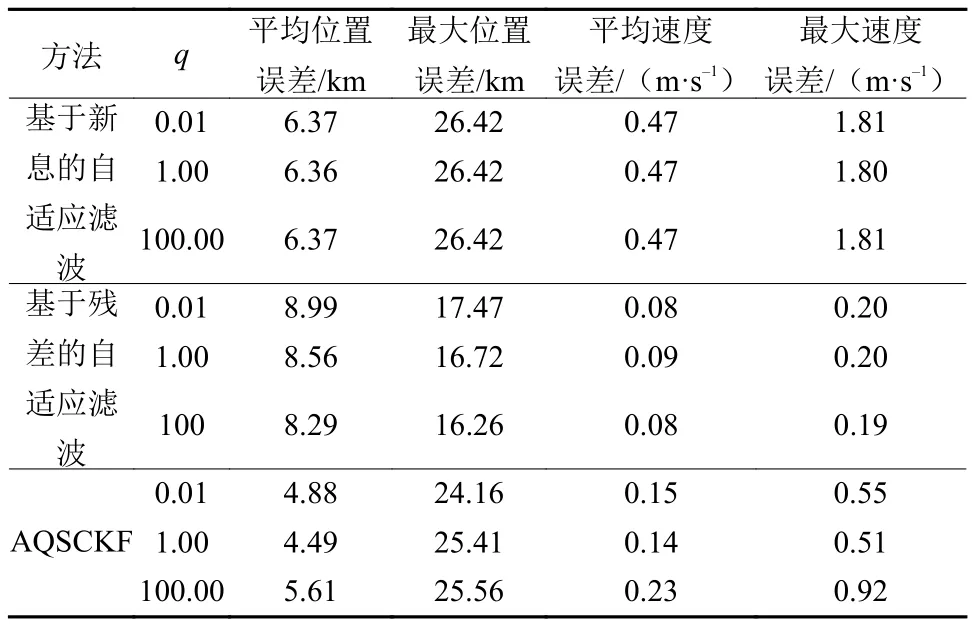
表3　基于新息和残差的自适应滤波与AQSCKF导航结果对比Table 3　The comparison of the adaptive filter based on innovation and residual and AQSCKF

从以上仿真结果可以看出，基于新息计算的调节因子的自适应方法几乎不受q值的影响，且其导航精度相对于传统SCKF滤波算法已经有了一定的提高。与此同时，基于残差计算的调节因子的自适应滤波算法相对于传统的SCKF算法也有了一定的提高。但在导航精度方面，二者虽然在不同程度上提高了导航精度，但提高有限。相比之下，AQSCKF算法在精度提高方面要远优于单独利用基于新息和残差的方法。

4　结　论

传统的利用新息或残差序列计算调节因子进而自适应调节过程噪声方差阵的方法，虽然一定程度上可以提供滤波的精度，但精度提高有限。本文从同时利用新息和残差信息来自适应调节过程噪声方差阵的角度出发，提出了另外一种同时基于新息序列和残差序列的计算的方法，即通过判断新息和残差的变化趋势来判断是否对Q阵进行自适应调节，当新息和残差的变化趋势一致时，调节因子的值为单独利用新息或残差调节时的调节因子的均值，若二者变化趋势不一致，则不对Q阵进行调节。仿真结果证明，本文研究的AQSCKF算法在深空探测器捕获段自主天文导航中，比单独利用新息或残差进行调节所获得的导航精度高。能够满足在深空探测器捕获段的复杂环境下，过程噪声不确定所带来的导航精度下降的问题。

［1］Bhaskaran S. Navigation of the Deep Space 1 spacecraft at Borrelly［Z］. AIAA paper，2002，4815：5-8.

［2］Bhaskaran S. Optical navigation for the stardust wild 2 encounter［C］//18th International Symposium on Space Flight Dynamics. German：［s. n.］，2004.

［3］Frauenholz R B. Deep impact navigation system performance ［J］. Journal of Spacecraft and Rockets，2008，45（1）：39-56.

［4］Bhaskaran S. Orbit determination performance evaluation of the deep space 1 autonomous navigation system［C］//AIAA/AAS Space Flight Mechanics Meeting. Monterey：AIAA，1998.

［5］Christian J A，Lightsey E G. Integrated performance of an autonomous optical navigation system for space exploration ［J］. Navigation，2010，2009：1.

［6］Woodard M. Orbit Determination of spacecraft in Earth-Moon L1 and L2 Libration Point Orbits［C］//AAS/AIAA Astrodynamics Specialist Conference. ［s. l.］: AAS/AIAA，2011

［7］Julier S J，Uhlmann J K. Unscented filtering and nonlinear estimation［J］. Proceedings of the IEEE，2004，92（3）：401-422.

［8］Arasaratnam I，Haykin S. Cubature kalman filters ［J］. Automatic Control，IEEE Transactions on. 2009，54（6）：1254-1269.

［9］Ge Q B，Li W B，Wen C L. SCKF-STF-CN：a universal nonlinear filter for maneuver target tracking［J］. Journal of Zhejiang University SCIENCE C. 2011，12（8）：678-686.

［10］Brunke S，Campbell M. Square root sigma point filtering for realtime，nonlinear estimation ［J］. Journal of Guidance，Control，And Dynamics，2004，27（2）：314-317.

［11］Ning X. Analysis of filtering methods for satellite autonomous orbit determination using celestial and geomagnetic measurement［J］. Mathematical Problems in Engineering，2012，2012：1-6.

［12］Tang X，Wei J，Chen K. Square-root adaptive cubature Kalman filter with application to spacecraft attitude estimation. in Information Fusion（FUSION）［C］//2012 15th International Conference on.［S.l.］：IEEE，2012.

［13］Stastny N B，Geller D K. Autonomous optical navigation at Jupiter：a linear covariance analysis ［J］. Journal of Spacecraft and Rockets，2008，45（2）：290-298.

［14］Lyzhoft J. GPU-Based Optical Navigation and Terminal Guidance Simulation of a Hypervelocity Asteroid Intercept Vehicle［C］//AIAA Cuidance，Navigation and Control（GNC）Conference. Washington DC：AIAA，2013:19-22

［15］Ahn H S，Won C H. Fast alignment using rotation vector and adaptive Kalman filter［J］. IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）：70-83.

［16］Yu M J. INS/GPS integration system using adaptive filter for estimating measurement noise variance ［J］. Aerospace and Electronic Systems，IEEE Transactions on，2012，48（2）：1786-1792.

［17］Hu C. Adaptive Kalman filtering for vehicle navigation ［J］. Positioning，2009，1（04）：0.

［18］Hide C，Moore T，Smith M. Adaptive Kalman filtering for low-cost INS/GPS［J］. The Journal of Navigation，2003，56（01）：143-152.

［19］Ding W. Improving adaptive Kalman estimation in GPS/INS integration ［J］. Journal of Navigation，2007，60（03）：517-529.

［20］Yang Y，Gao W. An optimal adaptive Kalman filter ［J］. Journal of Geodesy，2006，80（4）：177-183.

［21］Kallemeyn P. The Mars pathfinder navigation System ［J］. AIAA Paper，1996：96-3656.

通信地址：北京市海淀区学院路北京航空航天大学仪器科学与光电工程学院17系（100191）

电话：（010）82338820

E-mail：ningxiaolin@buaa.edu.cn

An Adaptive Kalman Filter for Mars Spacecraft Acquisition Phase

NING Xiaolin1，LI Zhuo1，HUANG Panpan2，YANG Yuqing1，LIU Gang1，FANG Jiancheng1
（1. School of Instrumentation Science & Opto-electronics Engineering，BeiHang University （BUAA），Beijing 100191，China；2. School of Civil and Environmental Engineering，University of New South Wales，Sydney 2052，Australia）

Celestial navigation is an energy saving and efficient way of autonomous navigation for deep space probes. Kalman filter has been successfully applied in the Celestial navigation system. During the acquisition phase，due to the complex dynamic environment，unmolded acceleration error and the ephemeris error etc. may cause the statistics of process noise uncertainty. To overcome the problem，a method named AQSCKF based on the trend of the innovation sequences and residual sequences to scale the process noise covariance matrix is proposed in this paper. In the first place，it calculates the scale factor based on the innovation and residual separately. Then，by comparing the trend of the two factors，the scale factor of the new method is set as the average. In addition，the navigation performance of traditional SCKF，the method only using innovation or residual to scale Q and AQSCKF is also compared by simulation. The simulation results show that the new method yields better performance than the traditional methods in solving the problem caused by the uncertainty of the process noise，furthermore it also shows a good stability.

adaptive filter；celestial navigation；process noise；Kalman filter

V249.32+3

A

2095-7777（2016）03-0237-8

10.15982/j.issn.2095-7777.2016.03.007

宁晓琳（1979—），女，副教授，博士生导师。主要研究方向：自适应滤波，航天器自主导航与控制技术，惯性导航，天文导航，视觉导航及组合导航，最优估计与信息融合。

［责任编辑：杨晓燕］

2016-05-26；

2016-06-19

国家重点基础研究发展计划（2014CB744202）