关于切割规则的可容许性定理的一个注释*

余 军 成，刘 明 元

关于切割规则的可容许性定理的一个注释*

余 军 成，刘 明 元

在《结构证明论》*Sara Negri & Jan von Plato. Structural Proof Theory[M]. Cambridge: Cambridge University Press, 2008.中，切割规则可容许性定理的证明在经典命题逻辑矢列演算中有四个问题：切割高度计算存在错误；“切割公式仅在左前提中是主公式”与“切割公式不是左前提的主公式”自相矛盾；收缩规则指代含混；“切割规则的任何一个前提不是逻辑公理”的表述不准确。文章分析这些问题并提出相关的解决方法，给出切割规则的可容许性定理一个详细而完整的证明，进一步论述经典命题逻辑矢列演算的子公式性质、一致性和可判定性。这些工作有助于提高学习和研究证明论的能力。

经典命题逻辑矢列演算；切割规则的可容许性定理；子公式性质；一致性；可判定性

作者余军成，男，汉族，重庆忠县人，贵州工程应用技术学院副教授，西南大学逻辑与智能研究中心博士研究生(毕节 551700)；刘明元，男，土家族，重庆酉阳人，西南大学逻辑与智能研究中心博士研究生(北碚 400715)。

一、引言

矢列演算(sequent calculus)是关于结论及其所依赖的假设之间的可推导关系的一种形式理论[1]P85。它广泛应用于证明论、数理逻辑、计算机科学、语言学、哲学，尤其是应用于自动化证明搜索系统(systems of automatic proof search)、逻辑编程(logic programming)中。根岑(Gerhard Gentzen)于1934～1935年最早提出矢列演算系统——经典谓词逻辑演算(根岑将该系统简称为“LK”)和直觉主义谓词逻辑演算(简称为“LJ”)[2], [3]。在LK 和LJ中，“主定理”(the Hauptsatz)”即切割消去定理(the cut-elimination theorem)保证任何一个LK 或LJ推导能够转换为另一个具有相同的末矢列但没有切割(Cut)推理图模式(即切割规则)出现的LK 或LJ推导[4]P298。它是矢列演算的核心结论，显示了建立矢列演算系统的重要性，对包括一致性等元理论成果具有深远的影响。因此，根岑给出了该定理的完整证明过程[5]P298-306。在LK 和LJ推导中，一方面，切割消去定理保证能够根据子公式性质(the subformula property)从根部(root)出发向上进行证明搜索；另一方面，正如布洛斯(George Boolos)所言，应用切割规则会极大地减少推导的长度[6]。

根岑的学生凯托宁[7](Oiva Ketonen)、克莱尼[8]P453(Stephen Cole Kleene)、柯里[9]P208-213(Haskell Brooks Curry)、内格里(Sara Negri)和柏拉图(Jan von Plato)[10]P25-60等在LK 和LJ的基础上，提出经典逻辑和直觉主义逻辑的矢列演算的各种变形系统。他们所提出的各种变形系统的逻辑规则与根岑提出的矢列演算系统的逻辑规则有很大的不同：在LK 和LJ中，并非所有的逻辑规则都是可逆的(invertible)。在经典命题逻辑矢列演算中，这些变形系统既有一个共同点：所有逻辑规则是可逆的并且都具有子公式性质；也有一个不同点：从有结构规则向没有结构规则转变。在有切割规则的变形系统中需要证明切割消去定理；在没有切割规则的变形系统中需要证明切割规则是可容许的(admissible)，即切割规则的可容许性定理。因此，有切割规则的矢列演算与没有切割规则的矢列演算如果两者是等价的，那么切割消去定理与切割规则的可容许性定理两者的作用是相同的。然而，在经典命题逻辑矢列演算变形系统中，凯托宁、克莱尼、柯里，内格里和柏拉图仅仅给出切割消去定理或切割规则的可容许性定理的部分证明，其中，内格里和柏拉图的证明较为详尽而易于接受[11]P54-57。在内格里和柏拉图的基础上，我们指出经典命题逻辑矢列演算系统(简称“G3cp*“G”是“甘岑系统”的缩写，“3”表示“没有结构规则”，“cp”是“经典命题逻辑”的缩写，“ip”是“直觉主义命题逻辑”的缩写。”)[12]P60中切割规则的可容许性定理证明有四个问题，我们分析了这些问题且提出相关的解决方法，给出切割规则的可容许性定理一个完整而详尽的证明，进一步论述了G3cp的子公式性质、一致性和可判定性。

二、G3cp系统

经典命题逻辑的语言L定义如下：

通过P, Q, R, … 表示的原子公式是公式，以及通过⊥表示的恒假是公式；如果A和B是公式，那么A∧B, A∨B, A⊃B是公式，此外，A=def(A⊃⊥)并且A⊃⊂B=def(A⊃B)∧(B⊃A)。

在G3cp中，矢列式的形式为Γ⟹Δ，其中，Γ和Δ是有穷的甚至可能为空的公式的多重集合(multisets)；其逻辑公理和逻辑规则如下所示[13]P49。

逻辑公理：

P,Γ⟹Δ,P

逻辑规则：

定义1*本文中加粗的“定义”、“定理”和“推论”采用顺序表示法，特此说明。：一个公式A的权重(weight)(简称“w(A)”)通过如下方式归纳定义，w(⊥)=0；对于原子公式P，w(P)=1；w(A∧B)=w(A∨B)=w(A⊃B)=w(A)+w(B)+1。

定义2：在G3cp系统中，一个推导或者是一个逻辑公理，或者是L⊥的一个实例(结论)，或者是一个逻辑规则应用到包含它的前提的推导；一个推导的高度是连续应用逻辑规则的最大数目，其中，逻辑公理和L⊥的推导高度为0。

说明：在G3cp系统中，对于任意的公式A、多重集合Γ和Δ，矢列式A,Γ⟹Δ,A是可推导的[14]P30-31；“nΓ⟹Δ”表示在推导高度至多为n时，矢列式Γ⟹Δ是可推导的；弱化规则和收缩规则是导出规则，都是保持高度可推导的[15]P53-54。

三、切割规则的可容许性定理证明存在的问题

在G3cp系统中没有结构规则，自然就没有切割规则，因而不需要证明切割消去定理。一个自然而然的问题：在G3cp系统中，为什么我们需要证明切割规则是可容许的呢？因为在我们的推理中，经常采用合成的证明，其中我们使用辅助的结论，它有助于我们缩短证明的过程。切割规则只不过是这种利用辅助结论的正式的对应物，它允许我们以正规的方式继续使用辅助引理[16]P24，从而极大地降低推导的高度。切割规则在G3cp系统中表现形式：

因此，需要证明该规则在G3cp系统中是可容许的；而且，我们发现内格里和柏拉图关于切割规则的可容许性定理证明存在以下四个问题：

(一)切割高度*在一个推导中切割规则的一个实例的切割高度(Cut-height)是该切割规则的两个前提的推导高度之和。计算存在错误

在“切割公式D在两个前提中是主公式”的两种子情况的证明过程中，出现了切割高度计算存在错误的问题。因为“与转换前的切割推导相比，转换后有较低切割高度的两个切割推导”[17]P56-57与“在其中切割公式在切割的两个前提中不是主公式的所有情况下，切割高度是减少的”以及“向上的切割排列不是一直减少切割高度而是可以增加它”[18]P35显然前后自相矛盾。如果详细计算切割高度，我们将会发现：转换后上面的一个切割的切割高度比转换前的切割高度减少；转换后下面的一个切割的切割高度与转换前的切割高度则无法精确比较究竟是减少还是增加。因而，证实了切割高度计算存在错误的问题。

(二)“切割公式仅在左前提中是主公式”与“切割公式不是左前提的主公式”自相矛盾

当“切割公式D仅在左前提中是主公式”时，我们需要考虑的是如何减少右前提D,Γ′⟹Δ′的推导高度。已知切割公式D不是右前提的主公式，因而，右前提的主公式要么在Γ′中，要么在Δ′中。“关于Δ=A⊃B,Δ′的L⊃”和“关于Δ=A∨B,Δ″的R∨”[19]P56显然指的是“左前提Γ⟹Δ,D的主公式在Δ中”(如果主公式在Δ中，则Δ=A⊃B,Δ′的L⊃规则显然是有问题的，因为Δ是左前提的后件，不可能是L⊃规则，而且Δ′与右前提的后件相互混淆。如果主公式在Γ中，那么有L⊃规则，但是，矢列式“Δ=A⊃B,Δ′”应改写为“Γ=A⊃B,Γ″”。因此，无论如何，“关于Δ=A⊃B,Δ′的L⊃”，要么规则运用有误，要么矢列式写法有误。此处，先撇开这两个错误)，即“切割公式D不是左前提的主公式”，显然与“切割公式D仅在左前提中是主公式”自相矛盾。

(三)收缩规则指代含混

在“切割公式D在两个前提中是主公式”的两种子情况*如果内格里和柏拉图呈现第一种子情况的证明，同样会出现收缩规则指代含混的问题。的证明过程中，还出现了收缩规则(简称“Ctr”)指代含混的问题。因为，Ctr规则是直觉主义命题逻辑矢列演算(简称“G3ip”)的导出规则：

在G3cp中，导出的收缩规则为：

收缩规则在G3ip和G3cp中显然是不同的，不能混用。因此，在G3cp中，关于“这两种子情况的证明过程”不可能会应用到G3ip导出的收缩规则“Ctr”，我们需要用“LC和RC”替换“Ctr”，否则，混用或者乱用收缩规则的现象将无法避免。

(四)“切割规则的任何一个前提不是逻辑公理”的表述不准确

除“切割规则的任何一个前提(即左前提和右前提)不是逻辑公理”之外，还应该包括“不是L⊥的结论”。因为它是与“切割规则的左前提是一个逻辑公理或L⊥的结论”以及“切割规则的右前提是一个逻辑公理或L⊥的结论”不同的第三种情况，这种情况显然不可能与前面两种情况有重合之处；在第三种情况的证明过程中，需要详细计算切割高度与L⊥的结论的推导高度为0(不需要计算切割高度)相矛盾。基于这两点理由，我们很容易断定内格里、柏拉图关于“切割规则的任何一个前提不是逻辑公理”的表述不准确，遗漏了“不是L⊥的结论”。

四、切割规则的可容许性定理的证明

定理3：切割规则，

在G3cp中是可容许的。它是该系统最重要的定理，因此需要详细考察该定理的证明过程。为了更好地解决以上四个问题，我们将给出一个详细而完整的切割规则的可容许性定理的证明。

证明：假定任给一个推导*假定推导的最上层矢列式从左到右的推导高度分别为n、m、k、…。的最后一步所应用的规则是切割规则，此外该推导中不再包含其他的切割规则，我们可以将该推导转换为一个具有相同结论但不包含切割规则的推导。对切割公式的权重以及子推导切割高度进行归纳。

我们首先要区分两种情况：一是切割规则的前提是逻辑公理或者L⊥的结论。二是切割规则的前提不是逻辑公理或L⊥的结论。然后再分别讨论两种情况的子情况，直至讨论完所有可能的子情况。

(一)切割规则至少有一个前提是一个逻辑公理或者L⊥的结论

1.切割的左前提Γ⟹Δ,D是一个逻辑公理或L⊥的结论

我们区分了三种子情况：一是切割公式D在Γ中。对右前提D,Γ′⟹Δ′运用弱规则(既包括左边的弱规则也包括右边的弱规则)可推导出Γ,Γ′⟹Δ,Δ′。

二是Γ和Δ含有相同的原子公式。那么，Γ,Γ′⟹Δ,Δ′也是一个逻辑公理。

三是⊥在Γ中。那么，Γ,Γ′⟹Δ,Δ′同样是一个L⊥的结论。

2.切割的右前提D,Γ′⟹Δ′是一个逻辑公理或L⊥的结论

二是Γ′和Δ′包括相同的原子公式。那么，Γ,Γ′⟹Δ,Δ′也是一个逻辑公理。

三是⊥在Γ′中。那么，Γ,Γ′⟹Δ,Δ′同样是一个L⊥的结论。

四是D=⊥。我们对左前提又区分了两种情况：(1)Γ⟹Δ,⊥是一个逻辑公理或L⊥的结论。那么，或者Γ和Δ含有相同的原子公式，或者⊥在Γ中，因此，Γ,Γ′⟹Δ,Δ′同样是一个逻辑公理或L⊥的结论。

(2)它是可推导的。⊥不可能是左前提Γ⟹Δ,⊥的主公式，因此，主公式要么在Γ中，要么在Δ中。我们又可以区分六种情况：Γ=A∧B,Γ″；Γ=A∨B,Γ″；Γ=A⊃B,Γ″；Δ=Δ″,A∧B；Δ=Δ″,A∨B；Δ=Δ″,A⊃B。

当Γ=A∧B,Γ″时，推导

A,B,Γ″⟹Δ,⊥L∧

转换为推导

1.发挥资源优势，做强冰雪旅游产业。冰雪旅游业是冰雪产业的主体，发展冰雪产业，首先要做强冰雪旅游业。吉林省应以冰雪资源优势为基础，以长吉都市、长白山、查干湖地区为中心，结合地域特色，实现错位有序发展，建成“一山、两城、三区”的冰雪旅游产业空间发展布局，构建知名冰雪产业品牌。

A,B,Γ″⟹Δ,⊥ ⊥,Γ′⟹Δ′Cut(n)

当Γ=A∨B,Γ″时，推导

A,Γ″⟹Δ,⊥ B,Γ″⟹Δ,⊥L∨

转换为推导

当Γ=A⊃B,Γ″时，推导

Γ″⟹Δ,⊥,A B,Γ″⟹Δ,⊥L⊃

转换为推导

当Δ=Δ″,A∧B时，推导

Γ⟹Δ″,A,⊥Γ⟹Δ″,B,⊥R∧

转换为推导

当Δ=Δ″,A∨B时，推导

Γ⟹Δ″,A,B,⊥R∨

转换为推导

当Δ=Δ″,A⊃B时，推导

A,Γ⟹Δ″,B,⊥R⊃

转换为推导

(二)切割规则没有前提是逻辑公理或者L⊥的结论

1.切割公式D在左前提Γ⟹Δ,D中不是主公式

在这种情况下，左前提的主公式要么在Γ中，要么在Δ中。我们可以区分六种情况：Γ=A∧B,Γ″；Γ=A∨B,Γ″；Γ=A⊃B,Γ″；Δ=Δ″,A∧B；Δ=Δ″,A∨B；Δ=Δ″,A⊃B。

当Γ=A∧B,Γ″时，推导

A,B,Γ″⟹Δ,DL∧

转换为推导

当Γ=A∨B,Γ″时，推导

A,Γ″⟹Δ,D B,Γ″⟹Δ,DL∨

转换为推导

当Γ=A⊃B,Γ″时，推导

Γ″⟹Δ,D,A B,Γ″⟹Δ,DL⊃

转换为推导

当Δ=Δ″,A∧B时，推导

Γ⟹Δ″,A,DΓ⟹Δ″,B,DR∧

转换为推导

当Δ=Δ″,A∨B时，推导

Γ⟹Δ″,A,B,DR∨

转换为推导

当Δ=Δ″,A⊃B时，推导

A,Γ⟹Δ″,B,DR⊃

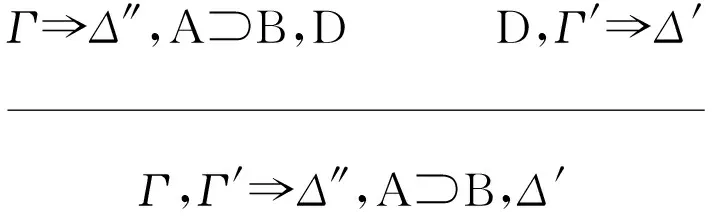
转换为推导

2.切割公式D仅在左前提中是主公式

切割公式D在右前提D,Γ′⟹Δ′中不是主公式，右前提的主公式要么在Γ′中，要么在Δ′中。我们可以区分六种情况：Γ′=A∧B,Γ″；Γ′=A∨B,Γ″；Γ′=A⊃B,Γ″；Δ′=Δ″,A∧B；Δ′=Δ″,A∨B；Δ′=Δ″,A⊃B。

当Γ′=A∨B,Γ″时，推导

D,A,B,Γ″⟹Δ′L∧

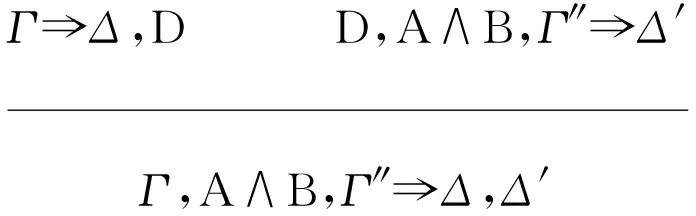
转换为推导

当Γ′=A∨B,Γ″时，推导

D,A,Γ″⟹Δ′ D,B,Γ″⟹Δ′L∨

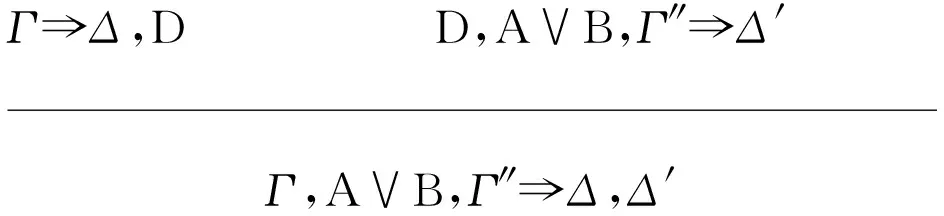
转换为推导

当Γ′=A⊃B,Γ″时，推导

D,Γ″⟹Δ′,A D,B,Γ″⟹Δ′L⊃

转换为推导

当Δ′=Δ″,A∧B时，推导

D,Γ′⟹Δ″,A D,Γ′⟹Δ″,BR∧

转换为推导

当Δ′=Δ″,A∨B时，推导

D,Γ′⟹Δ″,A,BR∨

转换为推导

当Δ′=Δ″,A⊃B时，推导

D,A,Γ′⟹Δ″,BR⊃

转换为推导

3.切割公式D在左前提和右前提中都是主公式

我们区分为三种情况：D=A∧B；D=A∨B；D=A⊃B。

当D=A∧B时，推导

转换为推导

Γ⟹Δ,A A,B,Γ′⟹Δ′Cut(n+k)

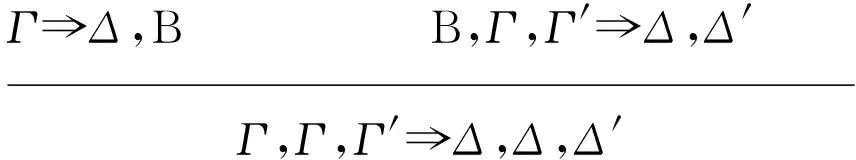
当D=A∨B时，推导

转换为推导

Γ⟹Δ,A,B B,Γ′⟹Δ′Cut(n+k)

当D=A⊃B时，推导

转换为推导

Γ′⟹Δ′,A A,Γ⟹Δ,BCut(m+n)

五、G3cp系统的推论

推论4：在G3cp中，关于矢列式在Γ⟹Δ推导中的所有公式是Γ和Δ的子公式[21]P57。因为G3cp没有结构规则，通过观察它的逻辑公理和逻辑规则，可以立即得出这一推论。

在证明论语义[22]的几种方法中，子公式性质是一种重要性质：如果矢列式Γ⟹Δ是可推导的且有切割消去定理作为保障，那么从根部出发利用逻辑规则向上进行证明搜索，一定存在这样一个推导，它的所有分支的最上层矢列式一定是逻辑公理或者L⊥的结论，而且推导中的所有公式是Γ和Δ的子公式。与有结构规则的经典命题逻辑矢列演算系统相较，G3cp系统一方面更适合自动证明搜索，因为它没有切割规则但同样具有子公式性质；另一方面切割规则的可容许性定理同样不仅可以简化向上证明搜索的步骤，而且针对同一逻辑的不同逻辑系统之间元理论的比较研究有至关重要的作用。

此外，如果一个系统承认关于“⟹”(或者⊥)的一个证明，那么该系统显然不具有一致性。因为，如果该系统有切割消去定理，那么关于“⟹”的证明就可以转化为不使用切割规则的“⟹”的证明，通过观察该系统的逻辑公理、逻辑规则以及不包括切割规则的其他结构规则，将会发现没有任何一个关于“⟹”的证明，这与承认有关于“⟹”的一个证明自相矛盾。在G3cp中，当Γ和Δ为空的多重集合时，“⟹”同样是不可推导的。因为，“⟹”既不是一个逻辑公理，也没有任何逻辑规则可以推导出它，也就是说，G3cp语形上是一致的。而且，关于任意一个矢列式Γ⟹Δ是不是可推导的，在G3cp中是可判定的：在一般的情况下，在G3cp中如果矢列式Γ⟹Δ是不可推导的，那么从根部出发利用逻辑规则向上进行证明搜索，关于它的所有可能的推导，其中，任何一个推导一定存在某个分支的最上层矢列式既不是逻辑公理也不是L⊥的结论；反之，则是可推导的。如果根据引理：在G3cp中，从矢列式Γ⟹Δ到最上层矢列式的分解是唯一的[23]P51，那么，如果它的最上层矢列式是逻辑公理或者L⊥的结论，则是可推导的；如果它的最上层矢列式既不是逻辑公理也不是L⊥的结论，则是不可推导的。因此，与一般情况相较，利用这个引理的优势在于，它可以大大简化如果矢列式Γ⟹Δ是不可推导的判定程序。

六、结语

在G3cp系统中，我们与内格里、柏拉图的不同之处在于：一是指出切割规则的可容许性定理证明存在四个问题；二是分析这些问题并提出相关的解决方法；三是给出切割规则的可容许性定理一个详细而完整的证明；四是进一步论述经典命题逻辑矢列演算的子公式性质、一致性和可判定性。这些工作有助于提高学习和研究证明论的能力。

[1]Sara Negri & Jan von Plato. Proof Analysis: A Contribution to Hilbert’s Last Problem[M]. Cambridge: Cambridge University Press, 2011.

[2]Gerhard Gentzen. Untersuchungen über das logische Schließen. I[J]. Mathematische Zeitschrift,1934,39,(2).

[3]Gerhard Gentzen. Untersuchungen über das logische Schließen. II[J]. Mathematische Zeitschrift,1935,39,(3).

[4][5]Gerhard Gentzen. Investigations into Logical Deduction[J]. American Philosophical Quarterly,1964,1.

[6]George Boolos. Don't Eliminate Cut[J]. Journal of Philosophical Logic, 1984,13,(4).

[7]Oiva Ketonen. Untersuchungen zum Prädikatenkalkül[D]. Helsinki, Annales Academiae Scientiarum Fennicae, Series A, I. Mathematica-physica,1944,23.

[8]Kleene, S. C. Introduction to Metamathematics[M]. Amsterdam: North-Holland Publishing Company, 1952.

[9]Curry, H. B. Foundations of Mathematical Logic[M]. New York: Dover Publications Inc, 1977.

[10][11][13][14][15][17][18][19][21][23]Sara Negri & Jan von Plato. Structural Proof Theory[M]. Cambridge: Cambridge University Press, 2008.

[12]Troelstra, A. S. and H. Schwichtenberg. Basic Proof Theory[M]. Cambridge: Cambridge University Press, 2000.

[16]Francesca Poggiolesi. Gentzen Calculi for Modal Propositional Logic[M]. Berlin: Springer, 2011.

[20]Hodes, H. T. Review[J]. The Philosophical Review,2006,115,(2).

[22]Reinhard Kahle and Peter Schroeder-Heister. Introduction: Proof-Theoretic Semantics[J]. Synthese, 2006.

责任编辑：陈 刚

ANoteontheAdmissibleTheoremoftheCutRule

YU Juncheng,LIU Mingyuan

In Structural Proof Theory, the proof of the admissible theorem of the cut rule in the sequent calculus of classical propositional logic shows four problems. First, there are cut-height calculative errors. Second, it is contradictory to postulate “the cut formula is principal in the left premise only” and “the cut formula is not principal in the left premise”. Third, the referent of the contraction rule is unclear. Fourth, the expression of “none of the cut premises is an axiom” is inaccurate. This paper analyses these problems and puts forward the relevant methods to solve them, gives a detailed and complete proof of the admissible theorem of the cut rule, and further discusses the subformula property, consistency and decidability of the sequent calculus of classical propositional logic. These jobs help to improve the ability of learning and studying proof theory.per

sequent calculus of classical propositional logic; admissible theorem of the cut rule; sub-formula property; consistency; decidability

B81

A

1003-6644(2016)05-0103-15

* 中央高校基本科研业务费专项资金一般项目“达米特直觉主义逻辑演绎思想研究”[项目编号：SWU1609140]；国家社会科学基金西部项目“中西方必然推理比较研究——以《九章算术》刘徽注为对象”[项目编号：11XZX009]。 * 郭美云教授阅读了全文，并指出文章的标题及引言的修改意见，特此致谢。