基于光学偏振试验的量子概念分析

栗　军，许士才，王吉华

(德州学院 物理与电子信息学院，山东 德州　253023)



基于光学偏振试验的量子概念分析

栗军，许士才，王吉华

(德州学院 物理与电子信息学院，山东 德州253023)

量子力学主要描述微小尺度下事物的行为，许多量子现象与人们日常直接经验相悖，因而量子力学的基本概念在教学过程中不容易被学生接受.偏振光实验是一个学生熟知、且实验现象直观的普通物理实验.本文着重从可观测量和测量的角度，通过对光学偏振实验现象的解释来阐述量子概念，使抽象的量子概念落实到对具体实验现象的归纳总结上来，有助于初学者认识和理解量子力学基本原理.

量子力学；量子测量；偏振

量子力学是近代物理学的基础，并且其应用领域已延伸至化学、生物等许多交叉学科当中，这一课程已成为当今大学生物理教学中一个极为重要的组成部分.由于量子力学主要是描述微观世界结构、运动与变化规律的学科，微小尺度下的许多自然现象与人们日常生活经验相距甚远，量子力学的概念有悖于人们的直觉，难以被初学者接受.如果在教学中能够结合具体的物理实验，从现象到本质引导学生思考，就可以使抽象的量子概念落实到对具体实验现象的归纳总结上来.

偏振光实验是一个现象直观而且学生容易操作的普通物理实验，在学生掌握的已有知识基础上，进行新内容的教学，符合初学者的认知规律.利用光的偏振现象来阐述量子力学基本概念已被一些国内外经典教材采纳，如物理学大师狄拉克所著的《量子力学原理》[1]，费因曼所著的《费因曼物理学讲义》[2]，曾谨言教授所著的《量子力学 卷1》[3]，赵凯华、罗蔚茵教授合著的《量子物理》[4]等教材.在本文中，笔者结合自己的教学体验，着重从可观测量和测量的角度来考虑问题，在以上经典教材的基础上，进一步整理和挖掘光子偏振所能体现的量子力学基本概念.从量子力学的角度对偏振实验现象进行分析，使同学们对态空间、量子力学表象、波函数统计解释、态叠加原理等量子力学概念有一个直观形象的认识，领会量子力学若干基本假定的内涵思想.最后，从量子角度分析了一个有趣的偏振光实验，

加深学

生对量子力学基本概念的理解，并展示了量子力学的奇妙特性.

1　偏振光实验的经典解释

如图1(a)所示，沿着光线传播的方向，顺次摆放两个偏振片P1、P2.光束经过P1后变为与其透振方向一致且光强为I0的偏振光.两偏振片P1和P2的透振方向之间夹角为θ，由马吕斯定律可知，透过偏振片P2的光的强度为I0cos2θ.按照经典的光学理论，此现象可理解如下：在一个与光传播方向垂直的平面内选定一个xy平面直角坐标系，这里为了描述问题的方便，选定x轴沿P2的透振方向.如图1(b)所示，透过偏振片P1的光电场矢量E可分解为两个分量：沿x方向振动的电场矢量Ex和沿y方向振动的电场矢量Ey.偏振光照射到P2偏振片时，投影到y方向的电场矢量被吸收，投影到x方向的电场矢量透过，振幅增加了一个常数因子cosθ，因而强度变为原来的cos2θ倍，这正是马吕斯定律所给出的结果.

图1

2　偏振光实验体现的量子力学概念

下面我们由偏振光的实验现象出发，引出量子态、态空间等量子概念，并用量子力学的语言来描述单个光子与偏振片发生相互作用的过程，讨论在多个光子情况下的量子行为与马吕斯定律的一致性.

2.1量子态

从实验得知，当线偏振光用于激发光电子时，激发出的光电子分布有一个优越的方向(与光偏振方向有关)，根据光电效应，每个电子的发射对应吸收一个光子，可见，光的偏振性质是与它的粒子性质紧密联系的，人们必须把线偏振光看成是在同一方向上偏振的许多光子组成，这样我们可以说单个光子处在某个偏振态上.沿x方向偏振的光束里，每个光子处在|x〉偏振态，沿y方向偏振的光束中，每个光子处在|y〉偏振态.假设我们在实验中把光的强度降到足够低，以至于光子是一个一个到达偏振片的.在图1所示的例子中，通过P1偏振片的光子处在沿P1透振方向的偏振态上，如果P2与P1透振方向一致(θ=0)，则此光子完全透过P2，如果P2与P1透振方向正交(θ=π/2)，则被完全吸收.如果P1与P2透振方向之间角度介于两者之间，会是一种什么样的情形，会不会有部分光子被吸收，部分光子透过的情况发生，但是实验上从来没有观察到部分光子的情形，只存在两种可能的情况：光子变到量子态|y〉，被整个吸收；或变到量子态|x〉，完全透过.下面我们用量子力学的语言来描述单个光子与偏振片发生相互作用的过程，引入量子测量、态空间、表象、态叠加原理、波函数统计解释等量子概念.

2.2量子测量、态空间、表象

单个光子与偏振片发生相互作用的过程，可以看成是一个量子测量的过程，偏振片作为一个测量装置，迫使光子的偏振态在透振方向和与其相垂直的方向上作出选择，测量的结果只有两个，透过或被吸收，透过光子的偏振方向与透振方向一致，被吸收光子的偏振方向与透振方向垂直，可见光子经过测量后只可能处在两种偏振状态，这正是量子特性的反应.在量子力学中，针对一个具体的量子体系，对某一力学量进行测量，测量后得到的值是这一力学量的本征值，我们称它为本征结果，相应的量子态坍缩到此本征结果所对应的本征态上，所有可能的本征态则构成一组正交、规一、完备的本征函数系，此本征函数系足以展开这个量子体系的任何一个量子态.很自然，我们在这里把经过偏振片测量后，所得到的两种可能测量结果(透过或吸收)作为本征结果，它们分别对应的两种偏振状态，此两种偏振状态可以作为正交、规一、完备的函数系，组成一个完备的态空间，任何偏振态都可以按照这两种偏振态来展开，展开系数给出一个具体的表示，这就涉及到量子力学表象问题.

在量子力学中，如果要具体描述一个量子态通常要选择一个表象，表象的选取依据某一个力学量(或力学量完备集)的本征值(或各力学量本征值组合)所对应的本征函数系，本征函数系作为正交、规一、完备的基矢组可以用来展开任何一个量子态，展开系数的排列组合给出某一个量子态在具体表象中的表示.结合我们的例子，组成基矢组的两种偏振状态取决于和光子发生相互作用的偏振片，具体说来是由偏振片的透振方向决定.在具体分析问题时，为了处理问题的方便，光子与哪一个偏振片发生相互作用，在数学形式上，就把光子的偏振状态按照此偏振片所决定的基矢组展开，这涉及到怎么合理选择表象的问题.

2.3态叠加原理、波函数统计解释

以上简单的试验也可以作为一个形象的例子来说明量子力学中的态叠加原理.态叠加原理的一种表述为[5]：设系统有一组完备集态函数{φi},i=1,2,...,t，则系统中的任意态|ψ〉，可以由这组态函数线性组合( 叠加) 而成，即

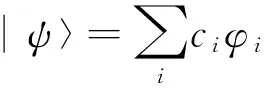
(1)

另一种描述为：如果{φi},i=1,2,...,t是体系可以实现的状态( 波函数)，则它们的任何线性叠加式总是表示体系可以实现的状态.在我们的例子中，任何一个偏振片所对应的透振态和吸收态构成完备集态函数，任何一个偏振态都能够在以此偏振片透振方向所决定的基矢组中展开，参照图1所示，通过偏振片P1的偏振态可以在以偏振片P2透振方向所决定的基矢组{|x〉,[y)}中表示为

|P1〉=cosθ|x〉+sinθ|y〉

(2)

相反， |x〉、|y〉基矢的任意叠加态也都是光子可能实现的偏振态.

量子力学还假定，当物理体系处于叠加态式(1)时，可以认为体系处于φi量子态的概率为|ci|2.从前面的分析我们知道，当用偏振片P2对偏振态|P1〉进行测量时，此状态随机地坍缩到|x〉偏振态或|y〉偏振态，坍缩到|x〉偏振态的概率为cos2θ，也就是单个光子透过偏振片的概率，多次统计的结果恰好与马吕斯定律相对应，这充分体现了波函数的概率统计解释.

3　典型例子

在教学中我们可以引入一个有趣形象的例子，进一步加深对量子力学基本概念的理解.如图2(a)所示，一束光入射到两个顺序排列的偏振片上，偏振片P3的透振方向相对于偏振片P1的透振方向顺时针转过90°角，我们不妨在一个与光传播方向垂直的平面内选定一个xy平面直角坐标系，P1的透振方向沿x轴，P3的透振方向沿y轴.光通过偏振片P1后变成光强为I0的偏振光，偏振方向与偏振片P1透振方向平行，但与P3的透振方向垂直，则光完全被偏振片P3吸收，不能透过.下面我们将看到一个有趣的现象，在偏振片P1和偏振片P3间插入一个偏振片P2，其透振方向在P1和P3之间，这时光竟可以透过P3偏振片.对此试验，我们可由马吕斯定律给出经典的解释.我们不妨设P2的透振方向相对于P1顺时针转过45°角，通过偏振片P1后，变为光强是I0的偏振光，且偏振方向与P1透振方向一致；再通过偏振片P2后，光强变为I0/2，偏振方向沿顺时针转过45°角，与偏振片P2透振方向一致；最后通过偏振片P3后，光强进一步减弱为I0/4，偏振方向又沿顺时针改变45°角，与偏振片P3透振方向一致.可以看到一个有趣的现象，虽然介于偏振片P1和P2间的光束其偏振方向与偏振片P3的透振方向正交，但最后透过偏振片P3的光束其偏振方向却恰恰沿偏振片P3的透振方向，这正是中间偏振片P2所起的作用.

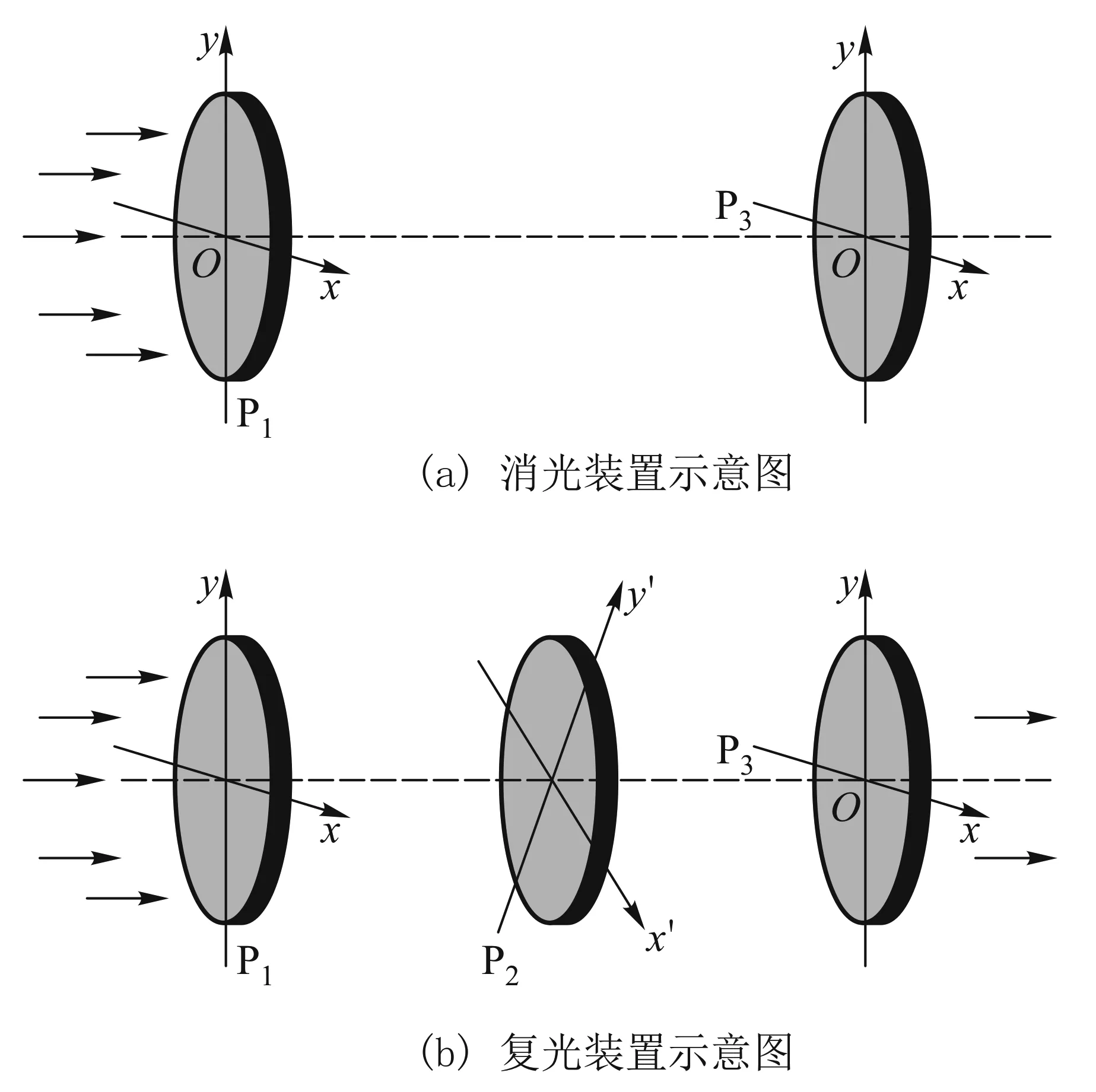
图2　装置示意图

下面用我们前面分析偏振光与偏振片相互作用过程中，所建立起来的量子概念给出具体解释.取直角坐标系xy，x轴沿偏振片P1的透振方向，基矢组为{|x〉,[y)}；由偏振片P2的透振方向所决定的基矢组为{|x′〉,[y′)}，其透振方向沿x′方向，如图3所示，两组基矢之间的关系可表示为

(3)

由偏振片P3所决定的基矢组仍为{|x〉,|y〉}，不过透过的光子处在|y〉基矢态.

图3　两组基矢之间的关系示意图

光子透过偏振片P1后，其偏振状态处在|x〉态，由式(3)，此状态可以按P2的基矢组展开为

(4)

根据式(4)，经过P2偏振片的测量，光子有1/2的概率坍缩到|x′〉态，光子透过P2，有1/2的概率坍缩到|y′〉态，光子被吸收.由式(3)，|x′〉态在由偏振片P3所决定的基矢组同样展开为

(5)

针对式(5)描述的光子偏振态，在偏振片P3的测量下，偏振状态发生改变，有1/2的概率坍缩到|y〉态，透过偏振片，有1/2的概率坍缩到|x〉态，被偏振片吸收，总体来说透过偏振片P1的光子有1/4的概率透过偏振片P3，与经典的马吕斯定律相一致.特别注意到光子透过偏振片P1后，状态为|x〉态，与|y〉态正交，没有|y〉态的组分，但光子透过偏振片P3后却正处在|y〉态，这充分体现了测量可以使量子态改变的量子假定，展示了量子测量的奇妙特性.

4　总结

结合对偏振光实验的量子解释，

我们分析了若

干重要的量子力学概念.但严格说来，光子的问题不属于量子力学问题，只有在量子场论中才能处理. 采用光子的偏振情形来讨论某些量子概念，理论上虽稍欠严谨，但如上文所述，确实能够直观形象地反映量子力学中的若干基本假定，使抽象的量子力学概念落实到对具体实验的分析中来，易于被初学者接受，我们不妨在学生开始学习量子力学时引入此例，有助于学生理解抽象的量子概念，领会量子力学的思维方式.

[1]狄拉克. 量子力学原理[M].北京:科学出版社，1966.

[2]费因曼.费因曼物理学讲义[M].上海:上海科学出版社，2005.

[3]曾谨言.量子力学 卷1. [M].北京:科学出版社，2006.

[4]赵凯华,罗蔚茵.量子物理[M].北京:高等教育出版社，2001.

[5]钱伯初.量子力学[M].北京:高等教育出版社，2006.

Analysis of quantum concept based on optical polarization experiment

LI Jun, XU Shi-cai, WANG Ji-hua

(College of Physics and Electronic Information，Dezhou University，Dezhou，Shandong 253023，China)

Quantum mechanics mainly describes the behavior of things at the micro scale. Many quantum phenomena are contrary to daily direct experience, so the basic concept of quantum mechanics is not easy to be understood by students in the course of teaching. Polarized light experiment is a common physical experiment, which is familiar to students, and the experimental phenomenon is intuitive. Focusing on the perspective of observable and measurement, this paper illustrates quantum concepts through the explanation of the phenomenon of optical polarization experiment. In this way, the abstract quantum concepts can be embodied in the analysis of the concrete experimental phenomenon, which will help students understand the basic principles of quantum mechanics.

quantum mechanics; quantum measurement; polarization

2015-07-28；

2015-11-04

国家自然科学基金(11304031)资助

栗军(1978—)，男，山东禹城人，德州学院物理与电子信息学院副教授，博士，主要从事量子力学教学及量子输运方向的研究工作.

O 413.1

A

1000- 0712(2016)03- 0005- 03