关于洛希极限下的引力辐射
韩胜强
(焦作师范高等专科学校 理工学院,河南 焦作 461400)
关于洛希极限下的引力辐射
韩胜强
(焦作师范高等专科学校 理工学院,河南 焦作461400)
指出了对于行星(或是卫星)绕主星体公转由于发射引力波损失动能而出现向主星体接近的速度,如果行星对主星体的洛希极限在主星体的外部,那么行星在由于引力辐射而向主星体接近的速度驱使下到达其洛希极限时就会被主星体的潮汐力所撕裂,引力辐射在此时终结,笔者计算给出了行星被撕裂的时间方程式.以太阳系中的土星为例子计算了它因引力辐射向太阳接近时被潮汐掉的时间,并将这一想法推广到相互绕转的双星系统或彗星.
引力辐射;洛希极限;接近;潮汐力;碎裂
关于动体的弱场引力辐射是由A.Einstein在他的广义相对论的著作中提出的[1].尽管有关引力波的理论工作在逐渐走向成熟,但在实验上并没有直接探测到,引力辐射和引力波的理论探讨和实验检测一直是引力研究领域的核心问题之一[2].美国科学家韦伯是首个用实验去检验引力波的人,他曾宣称检测到来自银河系中心的引力辐射,但后来没被证实.引力波的发现对我们了解宇宙起源意义重大.笔者在这里考虑了对于绕主星体公转发射引力波的行星(或卫星)在到达其洛希极限被撕碎而解体时引力辐射所终止的时间,在推广到双星或密度比较小的彗星时我们有必要考虑这一情况.
假设一个质量为m的行星绕着一个质量为M的主星体(或者视为恒星)以角速度ω公转,它们之间的距离为r,公转轨道近似为圆形.由于这颗行星有随时间变化的引力四极矩,那么它会发出引力辐射,即四极辐射.我们在Landau-Lifshitz关于引力场的能量动量表述的基础上,有弱场近似下的引力辐射功率为[3,4]
(1)

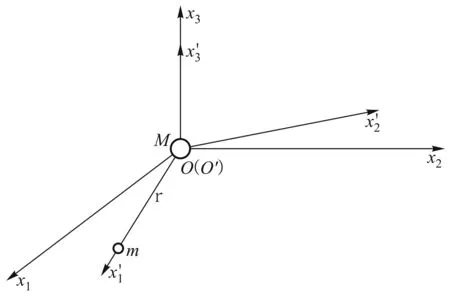
图1
(2)
为了描述行星m在实验室坐标系中的位置我们引入如下的坐标变换:
(3)
于是,行星在其主星体的引力场中做近似圆周运动的四极矩张量(为对称张量)为
Qij=∫mδ(x1-x10,x2-x20,x3)xixjdV
(4)
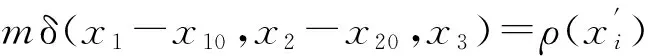
Q11(t)=∫mδ(x1-x10,x2-x20,x3)x1x1dV=
I11cos2ωt
(5)

Q12(t)=Q21(t)=I11cosωtsinωt
(6)
Q22(t)=I11sin2ωt
(7)
其余的Qij(t) 都为零.
由式(5)—式(7)可以得到行星的四极矩张量对时间的三阶导数为:
进一步得:
(8)
(9)
(10)
其中四极矩上的点表示对时间的微分,以上3个点代表对时间的三阶微分.
将式(8)—式(10)代入式(1)得到行星m的引力辐射功率公式:
(11)
引力场是保守场,行星在引力场中运动的总的能量是其动能与势能之和:
故行星由于引力辐射损失能量所引起的向主星体接近的速度为
(12)
将式(11)代入式(12)中得
(13)
由式(13)可以看出,行星辐射出能量后会向主星体靠近,距离越小接近的速度就越大.其实,这是由于行星的角动量在随时间减小,辐射场对质心的角动量在随时间而增加的缘故[6].
如果我们假设,这个行星对其主星体的洛希极限在主星体的外面,也就是说有如下关系成立:
RRoche>R0
其中,RRoche为行星对其主星体的洛希极限,R0为主星体的半径.那么行星由于引力辐射损失能量在向主星体接近时到达其洛希极限的时间为
整理后得到
作为例子,讨论太阳系中的土星,假设其在不受其他因素影响下,在因引力辐射损失动能而向太阳接近时到达其洛希极限时因太阳的引潮力而碎裂的时间.
由洛希极限表达式:
其中,M⊕为主星体质量,ρm为行星的密度.在我们讨论的这一情况下,太阳的质量为:M⊕=1.989×1030kg[7].土星的密度为:ρ0=700 kg·m-3,由此可以算出土星对太阳的洛希极限:
RRoche=1.267 228 129 051×109m
且有
RRoche>R⊙,(R⊙为太阳半径)
也就是说土星的洛希极限暴露在太阳的球体以外,土星向太阳靠近(由于引力辐射),那么在土星到达其对太阳的洛希极限时会因为太阳的引潮力而碎裂,土星的引力辐射会在此时终止.根据这些数据我们可以大致计算出这一时间为
t≈9.337 450 903 182 8×1024年
我们再次做出这样一个假设:如果土星的洛希极限没有暴露在太阳的球体之外,那么土星向太阳靠近并撞上太阳合并在一起,引力辐射在这样的情况下终止的时间为
计算后得
t′≈9.337 450 903 188 6×1024年
由此便可得出在这样的假设下,土星的引力辐射终
止的时间提前了:
Δt=t′-t
≈5.8×1012年
可见,这一提前的时间与总的时间相比数量级的差别是何等之大,显得微不足道.当我们看到这些数据之后会发现它们的数量级惊人,事实上这也不足为奇,因为我们太阳系中的土星辐射功率是非常小的.以至于要想将动能完全辐射掉所需要的时间甚至要远远大于我们现在所了解的宇宙的年龄.
在这里我们以太阳系的土星为例子来对这一想法做出说明,我们也可以把它应用到宇宙中的彗星、双星系统或其他星系团中去.对于那些洛希极限暴露在主星体外面的行星(或卫星)我们有必要去考虑这一因素.比如在1975年美国科学家J.泰勒和R.休斯首先发现的射电脉冲双星 PSR1913+16 ,有科学家估计它们因引力辐射而引起的相互接近(旋进)直至合并所需要的时间大约为:3亿年[8],如果伴星对主星的洛希极限大于主星体的球体半径,那么我认为这一时间有可能会提前.
[1]爱因斯坦.爱因斯坦文集(增订本)第二卷[M].范岱年,赵中立,许良英,译.北京:商务印书馆,2009:427-444.
[2]青心.对-谐条件下不存在引力辐射和引力波的研究[J].物理学报,2000,49(2).
[3]E.M.栗弗席兹,朗道.场论[M].任朗,袁炳楠,译.北京:人民教育出版社,1978.
[4]刘辽,赵峥.广义相对论[M].2版.北京:高等教育出版社2004:136.
[5]赵峥,刘文彪.广义相对论基础[M].北京:清华大学出版社,2010:110.
[6]汪定雄.引力辐射与角动量守恒[J].大学物理,1992,11(10):24-25.
[7]靳铁良.天体系统和粒子系统的相似性归纳[J].平顶山师专学报 2002,17(2).
[8]PSR B1913+16[EB/OL].http://zh.wikipedia.org/wiki/PSR_1913%2B16.
The gravitational radiation under the roche limit
HAN Sheng-qiang
(School of Science and Engineering,Jiaozuo Teachers College,Jiaozuo, Henan 461400, China)
This paper points out that a planet (or a satellite) revolving around a primary star may generate a velocity component towards the star because of kinetic energy loss due to gravitational wave emission and, if the Roche limit of the planet with respect to the primary star lies outside of the star surface, the planet, driven by the velocity component towards the star, will ultimately approach the Roche limit, where it is ripped apart by the tidal force and where the gravitational radiation terminates. The author gives an equation for computing the time at which the planet is ripped apart. A computation example is given using Saturn in the solar system as the study subject, in which the time of its ripping apart by tidal force is computed as it approaches the Sun under the influence of gravitational radiation. This philosophy is further generalized to binary stars that revolving around each other and to comets.
gravitational radiation; Roche limit; approach; tidal force; ripping apart
2015-06-13;
2015-11-12
韩胜强(1992—),男,河南周口人,焦作师范高等专科学校理工学院2012级专科生,学习和研究理论物理及宇宙量子现象.
大学生园地
O 412
A
1000- 0712(2016)03- 0054- 02

