互易定理教学研究
沈一骑 ,万 凯
(1. 南京大学 电子科学与工程学院,江苏 南京 210093;2. 南京大学 金陵学院 信息科学与工程学院,江苏 南京 210089)
互易定理教学研究
沈一骑1,2,万凯2
(1. 南京大学 电子科学与工程学院,江苏 南京210093;2. 南京大学 金陵学院 信息科学与工程学院,江苏 南京210089)
为帮助学生理解和应用互易定理,从纯线性电阻二端口网络的T型或Π型等效电路和定理的4种端口形式出发,指出理解电路互易和翻转后不同二端口电路在同一激励下的响应相等是掌握互易定理内涵的关键;提出“互易定理口诀”,以便于采用互易定理分析实际电路.
互易定理;互易定理内涵;互易定理口诀;实际电路分析
互易定理(Reciprocity theorem)[1]是电路理论中的一个重要定理,其本质是特勒根定理2(Tellegen’s theorem)[1],成立的条件是线性电阻网络仅为纯电阻电路,或由电阻和受控源构成的特殊电路[2].大一学生在学习互易定理时往往会对电路互易和电路翻转后的两个不同二端口电路中出现同一激励下响应相等感到困惑.又由于互易定理有3(4)种形式,常见习题又比较抽象和单一,学生在学习和应用时容易混淆,尤其是在采用互易定理分析实际电路时困难较大.对此,我们经过多年研究和教学实践,提出了解决这些难点的教学方法,以供同行参考和指正.
1 “互易定理口诀”
为清楚描述互易定理的4种形式并便于应用,表1给出了4种形式互易前后电路端口、激励和响应的形式及位置,以及由此推出的“互易定理口诀”.
以互易定理第三形式(“流短开压”)为例进行说明.第三形式的电路如图1所示.“流短开压”的第一字“流”表示互易前端口1的激励为电流源;第二字“短”表示互易前端口2的响应为短路电流;第三字“开”表示互易后端口1的响应为开路电压;第四字“压”表示互易后端口2的激励为电压源;中间两字所代表的响应短路电流和开路电压在数值上相等.定理其它形式的口诀不难由此类比解释.
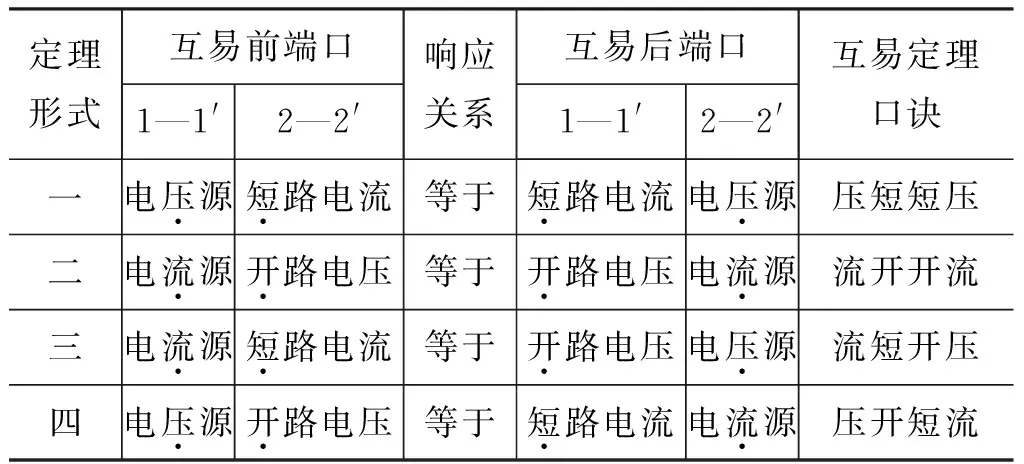
表1 互易前后电路激励和响应的形式及位置以及“互易定理口诀”

图1 互易定理第三形式
2 电路互易和翻转后响应相等的讨论
特勒根定理2也即特勒根拟功率定理,但不同理论教材的称谓各异,如特勒根第二定理[3]、特勒根定理[4]等,它表示在两个具有相同拓扑的电路中,一个电路的支路电流和另一电路的支路电压之间的相互关系.对于纯线性电阻电路,可由此直接推出互易定理,因而互易定理的本质是特勒根拟功率定理,这在理论上很容易理解,但对为什么会出现电路互易后在同一激励下响应相等、尤其是电路互易和电路翻转后不同二端口电路的响应也相等,理论教材[1, 3,4]未多作阐述.学生除了泛用特勒根拟功率定理来理解外,实际上仍是存疑的,这显然对理论教师和学生来说都是一个需要解决的重要课题.为把问题表述清楚,我们不妨先研究图2(a)所示的电路.图3(a)是原电路(图2(a))的互易电路,根据互易定理第一形式(“压短短压”)有I=I互易;而图3(b)是图2(a)的翻转电路,有I=I翻转,因此数学上有I互易=I翻转.
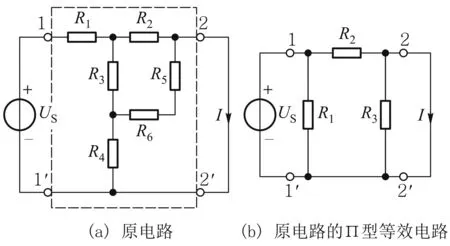
图2 电路互易和翻转讨论示例

图3 原电路的互易电路和翻转电路
引出的问题是,如果不考虑图3(a)、3(b)的端口标记,由于两图端口内的电路完全不同,为什么在其右侧端口加相同电压源后能得到左侧端口短路电流相等?而此时也难以直接采用特勒根拟功率定理,这正是学生在直觉上感到疑惑的地方.当然,如果端口内是具体电路,也不难通过计算得到I互易=I翻转;但如果端口内不是具体电路,则就难以计算了.此时如果再回到用“图3(a)是图2(a)的互易电路、图3(b)是图2(a)的翻转电路,因而I互易=I翻转”来解释;实际上并没有真正解答疑问.或许换一角度来理解更为合适.当然此问题实际上与为何有I=I互易等价,但因图2(a)、3(a)端口内电路相同可直接应用特勒根拟功率定理,故不易理解互易定理的内涵,也即为什么会有互易定理.
我们认为引入纯线性电阻二端口网络可等效为T型或Π型电路[1]的概念,对于理解这一问题较为有益.大一学生在学习互易定理时已熟悉一端口可等效为1个电阻,对于接受纯线性电阻二端口可等效为3个电阻的T型或Π型电路不会有太大困难.但如果直接采用纯线性电阻二端口的转移导纳相等进行解释,一则因(采用教材[1, 4]学习的)学生尚未学到二端口性质,二则又过于抽象而不易理解.况且互易定理与转移导纳相等的关系,即转移导纳相等是互易定理的结论还是成因,本身就是一个众说纷纭值得深究的问题.为直观明了起见,我们不妨将图2(a)等效为Π型电路(图2(b)),其互易和翻转电路仍为Π型电路,但端口内的电路是不同的(R1、R3的位置不同),如图4(a)、4(b)所示.

图4 原电路Π形等效电路的互易电路和翻转电路
由于此时为互易定理第一形式(“压短短压”)和Π型电路,图4(a)互易电路中的R1被“第一形式”中端口1的短路线所短路、R3在与“第一形式”中端口2的电压源并联等效中被舍去,即有I互易=US/R2;同理,图4(b)翻转电路中的R3被短路、R1被舍去,有I翻转=US/R2,故I互易=I翻转.因此,互易电路和翻转电路端口内的不同支路被互易定理的具体端口形式或短路或等效,真正起作用的仅是端口内互易或翻转前后不变的同一支路(图4中的不变支路为R2),也即互易电路和翻转电路的最终电路形式是相同的,这便是I互易=I翻转的最直观的解释.当然,如果将图2(a)等效为T型电路,则需通过计算才能得到I互易=I翻转,不如等效为Π型电路来得直观,而实际上T型和Π型电路本身即可进行等效变换.此外,对于互易定理的其他形式,也不难用类似的方法作出说明.因此,电路互易和电路翻转后不同二端口电路在同一激励下响应相等的原因,进而互易定理的内涵,完全可用纯线性电阻二端口的等效电路和定理的四种端口形式的具体组合进行解释,这或是理解的关键之一.由此可见,引入无源线性电阻二端口等效为T型或Π型电路的概念,方法虽然简单,但确能对理解互易定理、解答学习互易定理后产生的疑惑有所帮助.
3 互易定理在实际电路分析中的应用
一些理论教材[1]互易定理的习题比较抽象,学生往往不善于将互易定理应用于实际电路分析.下面通过示例介绍应用“互易定理口诀”的方法及其他要点.图5所示为双电源激励电路,如果用互易定理求解电流I,则须先应用叠加定理将电路化为单电源激励.
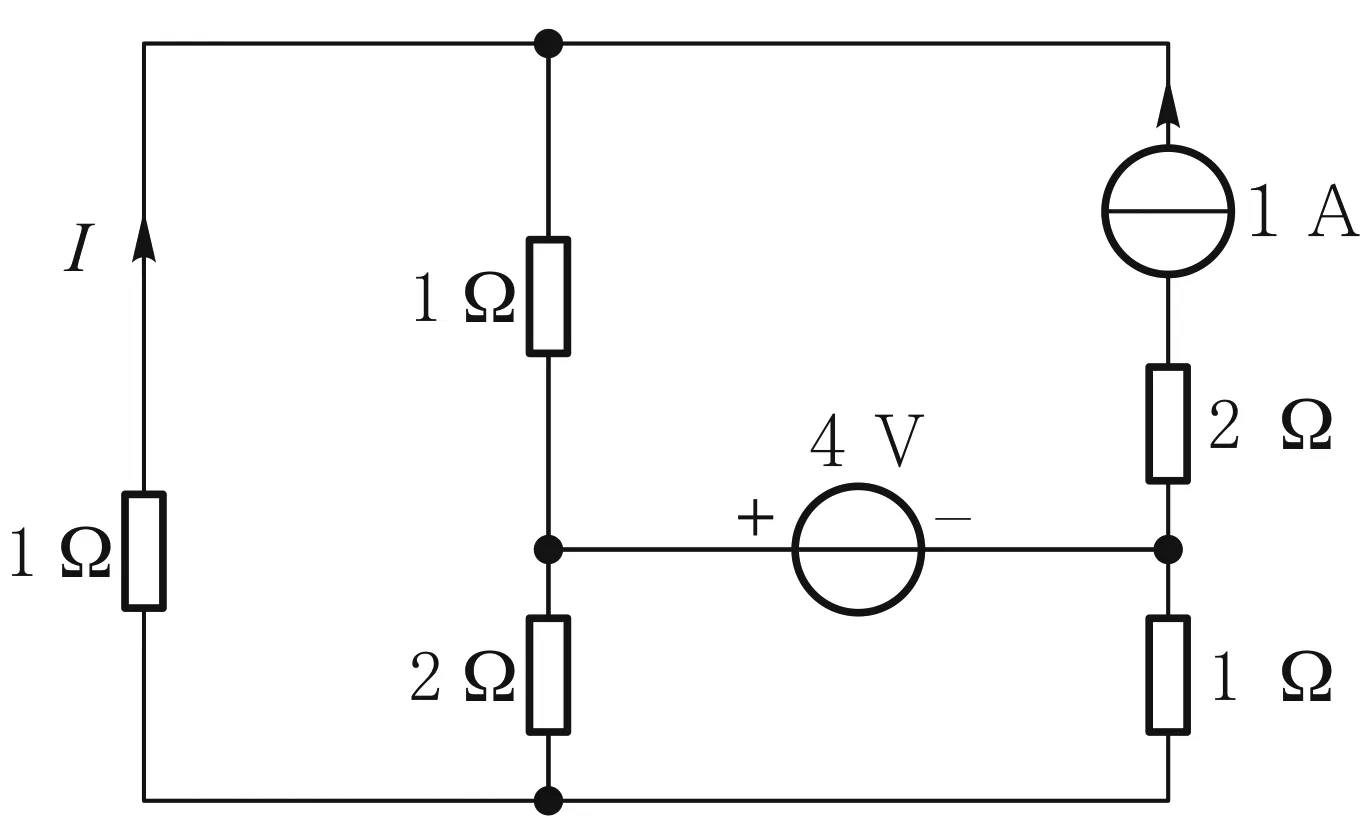
图5 互易定理应用示例

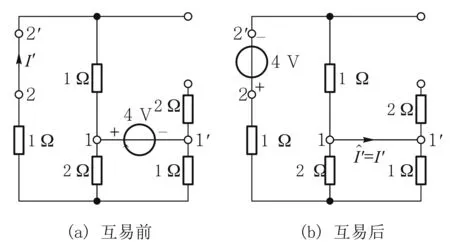
图6 4 V电压源作用时的互易(“压短短压”)


图7 1 A电流源作用时的互易(“流短开压”)

4 结束语
为帮助学生理解和应用互易定理,我们从纯线性电阻二端口网络的T型或Π型等效电路和定理的4种端口形式出发,分析了电路互易和电路翻转后不同二端口电路在同一激励下的响应相等的原因,这或是互易定理的内涵所在和理解的关键.提出了“互易定理口诀”,以方便将互易定理应用于实际电路分析.从多年的教学实践看,教学效果是比较理想的.
[1]邱关源.电路[M].4版.北京:高等教育出版社,1999:96-99,99-102,379-384.
[2]严利芳,郎文杰,刘朝阳.由一个特勒根定理例题的求解而引发的思考[J].电气电子教学学报,2008,30(4):19-20.
[3]陈洪亮.电路分析基础[M].北京:清华大学出版社,2009:174-177.
[4]江缉光.电路原理[M].2版.北京:清华大学出版社,2007:64-67.
2. School of Information Science and Engineering,Nanjing University Jinling College,Nanjing, Jiangsu 210089, China)
Teaching research on reciprocity theorem
SHEN Yi-qi1,2, WAN Kai2
(1. School of Electronic Science and Engineering,Nanjing University,Nanjing, Jiangsu 210093, Chian;
To help the students have a better understand and usage of reciprocity theorem, in this paper, we propose a reciprocity theorem table. Based on the four forms of the ports at reciprocity theorem and the equivalent circuit of two port network with pure linear resistance, we study the reciprocity theorem.It has been shown the instinct property of the theorem is the equivalent response between the reciprocity circuit and the reciprocal circuit.
reciprocity theorem; instinct property of the reciprocity theorem;reciprocity theorem table; circuit analysis
2015-06-29;
2015-10-13
江苏省高等学校教改研究课题(2013JSJG169)资助
沈一骑(1957—),男,浙江杭州人,南京大学电子科学与工程学院副教授,主要从事电路理论和实验的教学与研究工作.
教学经验交流
O 441.4
A
1000- 0712(2016)03- 0050- 04

