旋度概念的从头构建法
罗 凌 霄
(大理大学 工程学院,云南 大理 671003)
旋度概念的从头构建法
罗 凌 霄
(大理大学 工程学院,云南 大理671003)

矢量场;环量面密度;旋度
在矢量分析和场论中,旋度理论是建立在斯托克斯公式基础之上的,旋度概念的建立颇费周折[1].另外,旋度的确切含义也往往阐述得不清楚[2].更由于采用了不良的符号系统,导致公式不容易记忆,与物理学的衔接较差,导致电动力学、电磁场理论这些课里还须重讲旋度理论,造成了精力浪费.本文将通过新的途径,从根基上讲清楚旋度概念的由来和确切含义.并且指出计算矢量场沿无穷短线段的线积分时人们常犯的错误.
1 矢量场沿无穷小平面回路的线积分
矢量场f(r,t)是空间坐标和时间的函数,在某一空间区域Ω内,矢量场f(r,t)沿各个坐标轴的分量fxi(r,t)对各个坐标xj的偏导数∂fxi(r,t)/∂xj连续.如图1所示:P(x,y,z)是Ω内任意一点.n是任意的坐标轴,在过P点垂直于n轴的平面内作一无穷小

图1
回路l′圈围P点,回路光滑或者分段光滑,并且使回路的绕行方向与n轴方向符合右手螺旋关系.回路l′处于Ω内,P′(x′,y′,z′)是l′上的任意一点.我们把无穷小回路l′进一步细分为无穷多个线元,使每一个线元的长度与回路长度之比都趋于零.dl′是其中任意的一个线元矢量.

(1)
(2)
(3)
于是t时刻f沿回路l′的线积分(也叫做t时刻f沿回路l′的环量)为
∮l′f(P′)·dl′=∮l′fx(P′)dx′+
∮l′fy(P′)dy′+∮l′fz(P′)dz′
(4)
右边第一项
(5)
(6)
同理可以推出
(7)
(8)
根据分部积分公式可以推出
∮l′z′dy′=-∮l′y′dz′,∮l′x′dz′=-∮l′z′dx′,
∮l′y′dx′=-∮l′x′dy′
把式(6)—式(8)和上面3个关系式代入式(4),得
[ex∮l′y′dz′+ey∮l′z′dx′+ez∮l′x′dy′]
(9)
2 无穷小平面回路所圈围的面元矢量
ez(z′-z)]×(exdx′+eydy′+ezdz′)=

(10)
无穷小回路l′圈围的面元矢量为
+z∮l′dy′)+ey(∮l′z′dx′-z∮l′dx′-∮l′x′dz′+x∮l′dz′)+ez(∮l′x′dy′-x∮l′dy′-∮l′y′dx′+y∮l′dx′)]=
ex∮l′y′dz′+ey∮l′z′dx′+ez∮l′x′dy′
(11)
3 环量面密度
(12)

(13)
其中en表示n轴的方向矢量.上式也可表示为极限形式
(14)
其中l⊥n表示过P点与n轴垂直的平面内圈围P点的回路,其绕向与n轴方向符合右手螺旋关系.ΔSn是回路l⊥n圈围的平面面积.求极限时回路在此平面内从一切方向朝P点无限收缩.
所以,式(14)简写为
(15)
我们把左端的量叫做P点处与n轴垂直的平面内矢量场f(r,t)的环量面密度,也叫做P点处矢量场f(r,t)绕n轴的环量面密度.
4 旋度
环量面密度的清楚的定义是:过P点作垂直于n轴的平面,在此平面内作光滑或者分段光滑的回路l⊥n圈围P点,并且使回路的绕向与n轴方向符合右手螺旋关系.写出f(r,t)沿此回路的环量∮l⊥nf·dl与回路圈围的平面面积ΔSn的比值∮l⊥nf·dl/ΔSn,然后让回路在此平面内从一切方向朝P点无限收缩,算出比值的极限,此极限就定义为P点处矢量场f(r,t)绕n轴的环量面密度.矢量场f(r,t)中P点环量面密度概念成立的条件是f(r,t)的各个分量对各个坐标的偏导数在P点处连续.

5 结语
上述的旋度理论,不依赖于斯托克斯公式,斯托克斯公式反而是它的一个推论.把一个有限大小的回路所圈围的曲面分割为无穷多个平面面元,对每一个面元,式(12)都成立.把各个面元对应的式子全部加在一起,就可以推出斯托克斯公式.
式(12)给出了矢量场沿无穷小平面回路的线积分的简洁算法,但是它也掩盖了计算的细节.需要强调的是,计算矢量场f(r,t)沿无穷小回路的线积分时,即使回路是矩形状的,仍然需要把回路细分为无穷多个线元,使每一个线元的长度与回路长度之比都趋于零.矢量场f(r,t)沿无穷小矩形回路的一条边的线积分,并不等于这条边上任意一点处的f(r,t)点乘与这条边对应的线元矢量,但是在f(r,t)的分量对坐标的偏导数连续的情况下,它等于这条边中点处的f(r,t)点乘与这条边对应的线元矢量.
例如,对如图2所示的长为dx、宽为dy的逆时针绕向的无穷小矩形回路,矢量场f(r,t)沿AB边的线积分∫ABf(r,t)·dr,并不等于AB边上任意点处的f(r,t)点乘(-exdx),但是在f(r,t)的分量对坐标的偏导数连续的情况下,它等于AB边中点处的f(r,t)点乘(-exdx).
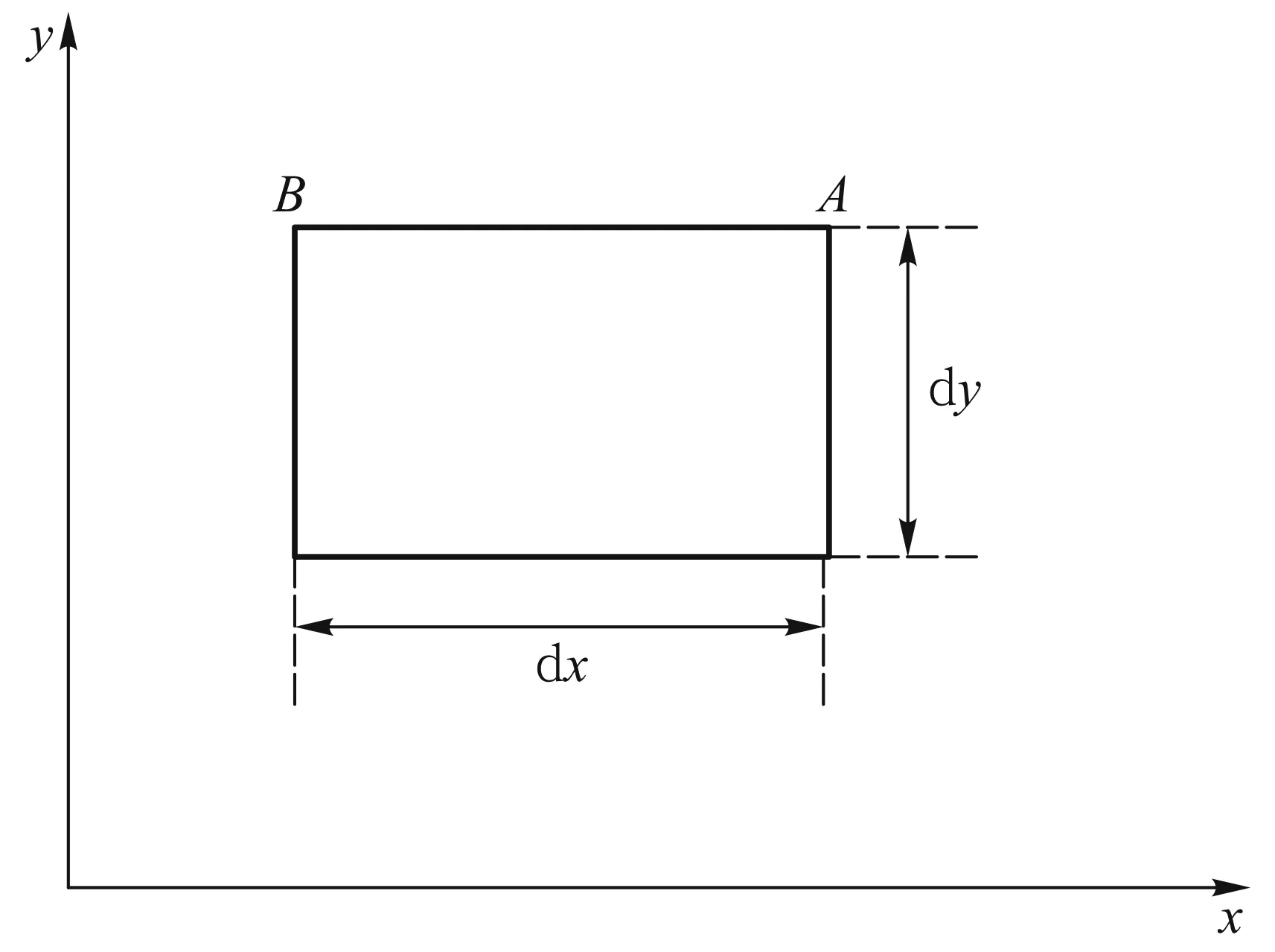
图2
AB边上任意点处的f(r,t)点乘(-exdx),与AB边中点处的f(r,t)点乘(-exdx),两者都是一阶无穷小量,并且可以证明,它们的差别是二阶无穷小量,似乎可以忽略它们之间的差别.但是现在我们的目的是计算矢量场沿无穷小矩形回路的线积分,它只是一个二阶无穷小量,所以计算矢量场沿无穷小矩形回路每一条边的线积分时,都应精确到二阶无穷小量,因此在这种情形下不能忽略AB边上任意点处的f(r,t)点乘(-exdx)与AB边中点处的f(r,t)点乘(-exdx)这两者之间的差别.
如果用无穷小矩形边上任意一点处的矢量场点乘此无穷短边对应的线元矢量所得结果来代替矢量场沿此无穷短边的线积分,用这样的4个点乘项之和代替矢量场沿矩形回路的线积分,那么环量的计算误差就达到和环量本身可以相比较的程度,
都是
二阶无穷小量,导致最终得出环量面密度竟然与4个点在无穷小矩形边上的位置(即它们对矩形边的分割方式)密切相关这一错误结论.
例如,对图2所示的回路,我们用上述错误的方法算得矩形中心处绕z轴的平行轴的环量面密度等于
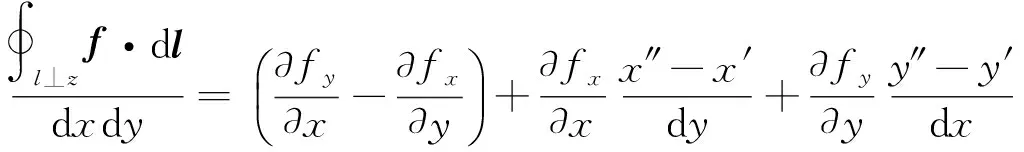


有的教科书在推导旋度公式时用了这个规律,但是没有意识到需要做出解释[3].
这是一条微妙的规律.我们将在下一篇论文中阐述这条规律,并且介绍它在电磁场切向边值关系中的应用.
[1]文丽,吴良大.高等数学(物理类.第二册)[M].北京:北京大学出版社,1990,326-352,119-122.
[2]同济大学数学教研室.高等数学(下册)[M].4版.北京:高等教育出版社,1996:214-224.
[3]杨宪章.工程电磁场[M].2版.北京:中国电力出版社,2011:17-19.
Building of curl concept from scratch
LUO Ling-xiao
(Faculty Engineering, Dali University, Dali,Yunnan 671003,China)

vector field; the surface density of circulation; curl
2015-07-02;
2015-10-31
罗凌霄(1964—),男,白族,云南剑川人,大理大学工程学院教授,主要从事电磁场理论的教学与研究工作..
O 411
A
1000- 0712(2016)03- 0008- 03

