基于试验模态法的直驱式超高压泵动态特性研究

张　祥，张仕进，余西伟，章伟成，曾令亮

（上海大学 机电工程与自动化学院，上海 200072）

基于试验模态法的直驱式超高压泵动态特性研究

张祥，张仕进，余西伟，章伟成，曾令亮

（上海大学 机电工程与自动化学院，上海 200072）

为得到直驱式超高压泵的动态特性参数，采用试验模态分析方法，对超高压水射流直驱式超高压泵的整体结构进行分析。在试验数据的基础上对频响函数进行优化，利用单模态参数识别法对直驱泵进行参数识别，获取整机固有频率、阻尼比和相应的振型。研究结果表明：直驱式超高压泵的固有频率集中在低频段（49.90， 100.21， 149.13， 175.93 Hz）和高频段（高阶模态频率大于1 000 Hz） ；薄弱环节主要集中在泵头阀部分；直驱式超高压泵在工作过程中，电机速度应避开981.8， 2 004.2， 2 982.6 r/min附近的3个速度范围。

试验模态分析；直驱式超高压泵；固有频率；动态特性

0　引言

直驱式超高压泵因具有节能、体积小等优点，而被广泛应用于超高压水射流、高压清洗设备中，以及采掘等领域。但其内部曲轴高速旋转和超高压水流的特点，使得直驱式超高压泵在工作时存在振动明显的情况，这对设备具有较大破坏作用。因此，改善直驱式超高压泵的振动状况，是提高直驱式超高压泵性能的重要途径。

模态分析是研究机械结构动力学的主要方法之一［1］，其中又分为计算模态分析和试验模态分析。计算模态分析又称理论模态分析，主要采用有限元方法研究激励、结构、响应三者的关系。国内外学者对此进行了大量研究，取得了较好的研究成果。试验模态分析则是利用参数识别的方法，研究激励信号和响应信号，并获得固有频率、阻尼比和振型等模态参数［2］。

本文采用试验模态法对直驱泵进行动态特性研究，利用最小二乘法对其频响函数进行优化，在数据处理时利用单模态参数识别方法对直驱泵进行模态参数识别。

1　直驱泵的基本结构及工况

超高压水射流直驱式超高压泵为三柱塞往复泵，其与电动机、进出水管道等设备共同组成超高压水射流系统，如图1所示。直驱泵由电动机通过带轮直接驱动泵内曲轴，曲轴带动连杆通过十字头与柱塞连接作往复运动。柱塞在曲轴带动下作回程运动时，液缸容积逐渐增大，形成局部真空，在压差作用下，进水口单向阀打开，水进入液缸内，完成吸水过程。当柱塞作进程运动时，液缸内容积逐渐减小，水受挤压，压力增加，使进水口单向阀关闭，出水口单向阀打开，水从高压出水口排出。由于柱塞不断地往复运动，吸排水过程就不断地交替进行，高压水不断输出。

在直驱式超高压泵工作过程中，主要振动来自于电机轴旋转、曲轴旋转、连杆往复运动、进出水口单向阀开闭、进出水流量脉动。

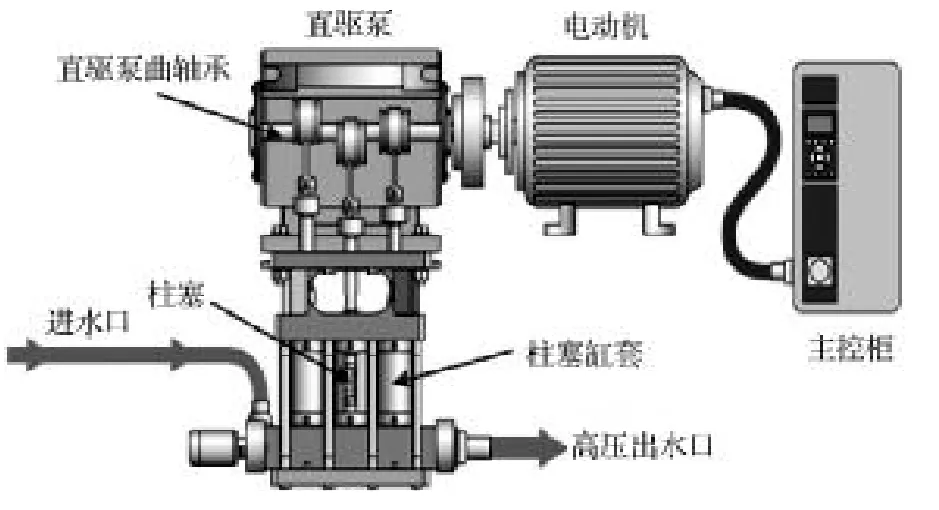
图1　超高压水射流高压泵系统Fig. 1　UHV water-jet super pressure pumps system

2　直驱泵的试验模态分析

2.1试验模态分析方案

试验研究对象为上海狮迈科技有限公司生产的LTJ1613-5B型五轴水射流超高压直驱泵，具体试验方案如图2所示。

试验主要仪器有：MI-7008数据采集分析仪，杭州忆恒科技有限公司；Dytran3263A三向加速度传感器，美国Dytran仪器公司；5800B5力锤，美国Dytran仪器公司；笔记本电脑1台。模态试验测试流程如图3所示。

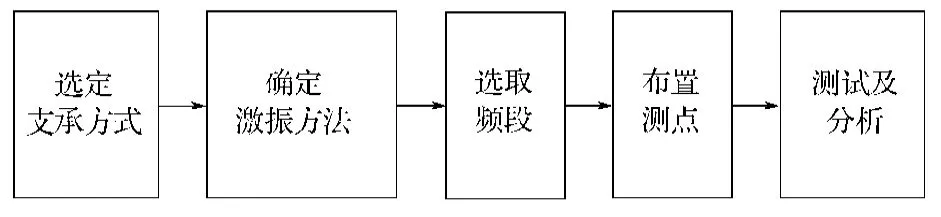
图2　直驱泵模态试验方案Fig. 2　A modal testing program for direct-driven pumps

图3　模态试验测试及分析流程Fig. 3　The modal testing and its analytical process

直驱式超高压泵的支承方式可选择自由状态和工作状态2种。由于研究对象为直驱式超高压泵本体，为获得其真实模态参数，试验采取自由悬挂支承方式。考虑到激振器装置的成本高，测试过程较复杂，而力锤传感器具有施加激励方便、测试响应速度快的优点，因此激振方式采用锤击法［3］。锤击时可选择单点激励多点响应或多点激励单点响应2种方式，且都能准确获得结构模态参数。鉴于直驱式超高压泵结构复杂，传感器布置不变的情况，试验采用多点激励单点响应的方式采集数据。

为充分展现直驱式超高压泵固有频率的分布情况，在对直驱式超高压泵进行有限元分析的基础上，根据采样定理，试验选择0～4 000 Hz作为分析频段。为了直观表明直驱泵的振型情况，精确得到试验数据，测点的布置应体现直驱泵的外部轮廓，因此直驱式超高压泵整机共布置112个激励点并作数字标记。因直驱式超高压泵振动主要集中在动力端（曲轴）和液力端（柱塞、泵头阀），因此测点布置时，在动力端和液力端较其他部位集中，如图4所示。三向加速度传感器布置在测试点5所在的位置，如图5所示，总体试验布局如图6所示。

图4　测试点布置Fig. 4　The layout of measuring points

图5　加速度传感器布置Fig. 5　The layout of acceleration sensors

图6　模态试验布局Fig. 6　The layout of the modal test

2.2模态试验数据采集

锤击时，采用多点激励单点响应的方式采集信号：先固定三向加速度传感器，采集测试点5的x， y，方向的数据；同时移动力锤传感器，按照测试点序号依次锤击。为提高数据采集精度，避免电信号干扰，将采集分析仪接地。

实时监测激励信号是否具有连击，把握锤击力度，尽量避免与锤击表面粘连时间过长，造成连击。若有连击，说明脉冲激励时间过长，得到的数据干扰太大，数据不具有可信度，属于无效信号。无连击激励信号时域图如图7所示，激励信号在1 ms内被采集完毕（一次锤击力度为150 N）。检查力锤信号相干性是否良好，若相干系数接近于1，表明试验过程中所受干扰小，所得试验数据可靠性高。如图8所示，各频率对应的相干系数均大于工程取值0.75，可视为相干性良好。对同一激励点多次敲击，选取各方面验证条件最好的3组数据的平均值作为该点的试验取值。

图7　激励信号时域图Fig. 7　Time domain diagram of excitation signals

图8　相干系数示意图Fig. 8　Schematic diagram of coherent coefficients

2.3模态试验数据处理

试验数据采集后，经快速傅里叶变换，得到激励信号和响应信号各自的自功率谱和平均互功率谱，进而确定频响函数［4］。由于测试中的噪声和估计中的误差，需要对频响函数进行优化处理［5］，优化方法如下。

频响函数误差列阵为

按照最小二乘法的思想，总方差E最小即得目标频响函数的估计值。

对频响函数进行优化处理后，可得频响函数幅频图，如图9所示。由图可知，其幅频峰值集中在200 Hz以内。

图9　频响函数幅频图Fig. 9　Frequency diagram of the frequency function amplitude

3　模态试验数据处理

3.1模态试验结果

对优化之后的频响函数进行参数识别，参数识别方法主要有频域法和时域法2种。频域法技术成熟，不会遗漏模态，也不会产生虚假模态，因此试验采用频域法中的单模态参数识别法，对试验数据作模态参数识别。

对直驱式超高压泵整机112个测试点的频响函数，进行拟合分析和参数识别后，可得出直驱式超高压泵各阶模态参数。由于高阶模态对结构的影响较小，因此只取需重点关注的前4阶固有频率、阻尼比，如表1所示。

表1　各阶模态的固有频率和阻尼比Table 1　The modal natural frequency and damping ratio

为了确定所测模态参数是否有效，需要利用模态置信准则 （modal assurance criteria，MAC）对所测模态参数进行验证［6］。模态置信准则的作用是判定2个模态向量和之间是否具有相关性，与之间的MAC值定义为

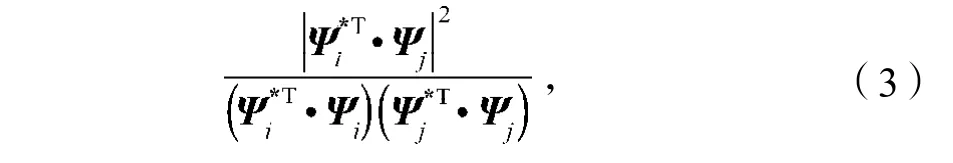
式中：*表示对向量求共轭；T表示转置。

如果2个模态向量为同一物理振型估计，那么式（3）的计算值接近于1；如果2个模态向量为不同的物理振型估计，式（3）的计算值接近于0。

试验所用的数据采集分析仪自带MAC分析，对所测得模态参数进行分析后获得MAC柱状图，如图10所示。从图10中的MAC柱状图可以看出，对角线模态向量自身的MAC值为1。试验所关注的前4阶模态中，各阶模态向量之间的MAC值小于0.4，这说明模态向量相互之间为不同的物理振型估计，可以进行下一步的模态振型分析［7］。

图10　模态置信准则分析柱状图Fig. 10　Bar charts of modal assurance criteria analysis

3.2振型分析

利用MI-7008数据采集分析仪自带的三维建模软件，先建立直驱式超高压泵的点线框模型（图11a），其中点的布置为实际测试点的位置，数字标号为实际测试点数据标号（图11b）。再将各点对应的频响函数数据赋值于直驱式超高压泵点线框模型后进行振型分析，结果如图12所示。

直驱泵的第一阶固有频为49.09 Hz，其模态振型表明，振动主要集中在泵头阀处，沿y方向上下振动明显，泵头阀两端将首先产生破坏。第二阶固有频率为100.21 Hz，在外加激励频率接近100.21 Hz时，振动主要集中在泵头阀和柱塞缸套处，沿x方向左右摆动。第三阶固有频率为149.13 Hz，振动集中在泵头阀处，沿y方向上下振动，破坏集中在泵头阀两端。第四阶固有频率为175.93 Hz，从第四阶振型可以明显看出直驱泵动力端（曲轴）为主要薄弱部分，分别沿x和y方向振动明显，若外加激励在175.93 Hz附近，将对其造成极大破坏。

对直驱式超高压泵振型总体分析可知，前3阶模态振型均出现在泵头阀部分，这表明直驱式超高压泵泵头阀部分刚度较薄弱，这与其内部构造（图13）密不可分。因泵头阀部分零部件多，内部结构复杂，相互之间结合面多，其整体动刚度较小，因此其动态特性较差，在受到与之固有频率相近的激励力时，破坏首先发生在液力端部分。而在第四阶模态振型中，由于其固有频率较高，来自电机和曲轴自身旋转的激励频率较小，正常工作状态下影响不大。

在直驱式超高压泵工作时，进出水口单向阀反复工作，进出水按图13中箭头方向反复进出。如果进出水流量脉动频率与其固有频率接近，泵体共振振幅将在其流量脉动方向上达到最大，造成泵头阀损坏。因此有必要对直驱式超高压泵工作状态下的振动状况进行分析。

图11　直驱泵点线框模型及测试点布置Fig. 11　The layout of dotted line model and test points of direct-driven pumps

图12　直驱泵振型分析结果Fig. 12　The analysis result of vibration mode of direct-driven pumps

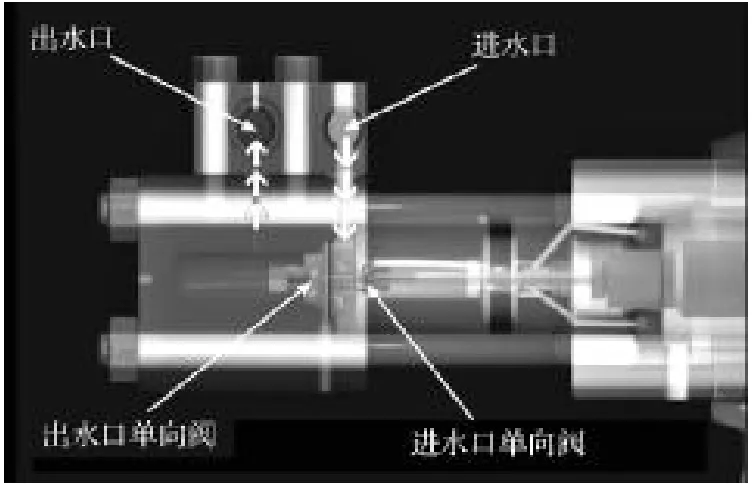
图13　泵头阀内部结构示意图Fig. 13　An internal structure diagram of head valves

3.3工作状态下的泵体振动分析

在模态试验取得直驱式超高压泵固有频率及相应振型后，再对泵体在工作状态下的振动进行分析。设电机转速为n1，电机输出的减速比1:2，则直驱式超高压泵曲轴转速n2=n1/2，曲轴振动频率

多缸流量脉动曲线如图14所示。由图可知，三缸往复泵在一个往复周期内进出水共6次，其流量脉动频率f2=6f1。因此，直驱式超高压泵泵头阀处进出水流量脉动频率

图14　多缸往复泵流量脉动曲线示意图Fig. 14　A curve diagram of the flow pulsation of multi-cylinder reciprocating pumps

对直驱式超高压泵影响最大的为第一阶模态固有频率。如果所接入电机由于选型或转速调节不合理，泵体曲轴振动频率与流量脉动频率接近第一阶固有频率49.09 Hz时，会产生共振，从而造成设备损坏。假设曲轴振动频率f1=49.09 Hz，代入式（4）得电机转速n1=5 890.8 r/min。在现有2， 4， 6， 8级电机中，最大转速为3 000 r/min，因此可忽略曲轴共振。假设泵头阀流量脉动频率f2=49.09 Hz，将其代入式（5）中可得电机转速为n1=981.8 r/min。在电机的选型或转速调节时，应避免其转速在n1=981.8 r/min附近。同样地，如果假设泵头阀流量脉动频率分别与直驱式超高压泵的第二阶和第三阶固有频率相同，通过计算可得，电机转速分别为2 004.2 r/min和2 982.6 r/min。在电机的选型或转速调节时，同样应避免其转速在2 004.2 r/min和2 982.6 r/min附近。

4　结语

本文以直驱式超高压泵为试验对象，详细论述了试验模态法的基本原理和方法，获得了直驱式超高压泵前4阶固有频率和阻尼比。结合模态试验数据，建立了直驱式超高压泵点线框模型，直观展现了直驱式超高压泵的动态特性和薄弱环节。结合模态试验和泵体振动分析，得出了直驱式超高压泵泵头阀为主要薄弱部分的结论。在设计泵头阀阀门组件与柱塞缸套时，应注意简化结构，减少结合面数量。在加工零件时，要提高加工精度，提高结合面处刚度，改善泵头阀处动态特性。直驱式超高压泵在工作过程中，为避免由于激励频率与固有频率相近所产生的共振破坏，电机速度应避开981.8， 2 004.2，2 982.6 r/min附近的3个速度范围。

［1］徐猛，张俊红，王琪，等. 白车身及内饰车身的试验模态对比分析及动力学评价［J］. 机械设计，2014，31（8） ：40-44. XU Meng，ZHANG Junhong，WANG Qi，et al. Experimental Modal Comparative Analysis and Dynamic Characteristic Evaluation of Body-in-White and Trim Body［J］. Journal of Machine Design，2014，31（8） ：40-44.

［2］周莉，李爱萍，古志勇，等. 基于实验模态分析的机床动态性能测试［J］. 中国工程机械学报，2014，12（4） ：360-363. ZHOU Li，LI Aiping，GU Zhiyong，et al. Dynamic Performance Testing on Machine Tools Via Experimental Modal Analysis［J］. Chinese Journal of Construction Machinery，2014，12（4） ：360-363.

［3］刘军，高建立，穆桂脂，等. 改进锤击法试验模态分析技术的研究［J］. 振动与冲击，2009，28（3） ：174-177. LIU Jun，GAO Jianli，MU Guizhi，et al. An Improved Experimental Modal Analysis System with Hammering Method［J］. Journal of Vibration and Shock，2009，28（3） ：174-177.

［4］ JIN Yong，ZHENG Linliu. The Experimental Modal Analysis of Water-Lubricated Rubber Stern Bearing［J］. Applied Mechanics and Materials，2011，66/67/68：1663-1667.

［5］徐向阳，朱才朝，张晓蓉，等. 大功率船用齿轮箱试验模态分析［J］. 振动与冲击，2011，30（7） ：266-270. XU Xiangyang，ZHU Caichao，ZHANG Xiaorong，et al. Experimental Modal Analysis of Heavy Duty Marine Gearbox［J］. Journal of Vibration and Shock，2011，30（7） ：266-270.

［6］李业聪. 曲轴-飞轮组合的模态分析及优化［D］. 南宁：广西大学，2013. LI Yechong. Modal Analysis and Optimization of Crankshaft-Flywheel Combo［D］. Nanning：Guangxi University，2013.

［7］张喜清，项昌乐，刘辉，等. 基于预试验分析的复杂箱体结构试验模态研究［J］. 振动与冲击，2011，30（4） ：109-112. ZHANG Xiqing，XIANG Changle，LIU Hui，et al. Modal Testing Study on a Complicated Housing Structure Based on Pre-Tests Analysis［J］. Journal of Vibration and Shock，2011，30（4） ：109-112.

（责任编辑：邓光辉）

On the Dynamic Characteristics of Direct-Driven Super Pressure Pumps Based on an Experimental Modal Analysis

ZHANG Xiang，ZHANG Shijin，YU Xiwei，ZHANG Weicheng，ZENG Lingliang
（School of Mechatronic Engineering and Automation，Shanghai University，Shanghai 200072，China）

To obtain the dynamic parameters of direct-driven super pressure pumps， an experimental modal analysis has been made of the overall structure of direct-driven pumps. The frequency response function is optimized based on the analysis of the experimental data， and a single-mode parameter identification method has been adopted to identify the parameters of direct-driven pumps， thus obtaining the machine inherent frequencies， damping ratio， and the corresponding mode shape. The research results show that the inherent frequency of super pressure direct-driven pump mainly concentrate in the low frequencies （49.90， 100.21， 149.13， 175.93 Hz） and high frequency （with a high mode frequencies above 1 000 Hz）； while the weak links mainly concentrate on the valves. During the operating process of direct-driven super pressure pumps， three ranges of speed， 981.8， 2 004.2， and 2 982.6 r/min should be avoided by the motor speed.

experimental modal analysis ；direct-driven super pressure pumps ；inherent frequency ；dynamic characteristics

TH322

A

1673-9833（2016）03-0024-06

10.3969/j.issn.1673-9833.2016.03.005

2016-04-03

张祥（1990-），男，河南安阳人，上海大学硕士生，主要研究方向为机械制造及CAE，E-mail：Jasonzhang323@foxmail.com