带硬时间窗的共同配送车辆调度问题研究
宾 厚,王 缙
(湖南工业大学 商学院,湖南 株洲 412007)
带硬时间窗的共同配送车辆调度问题研究
宾厚,王缙
(湖南工业大学 商学院,湖南 株洲 412007)
针对带硬时间窗的共同配送车辆调度问题,提出Sweep算法和PMX算子相结合的遗传算法。以长株潭城市群生鲜食品共同配送中心区域内的配送数据作为实验对象,采用组合遗传算法进行分析,在客户要求的时间范围内,合理安排车辆的行驶路线,使共同配送总费用最低。最后,将本算法与启发式算法、遗传算法进行比较,分析结果表明,本算法得到的共同配送车辆调度方案更优。
硬时间窗;共同配送;车辆调度
0 引言
随着国民经济的迅速发展、人民生活水平的提高,消费者的需求日益多样化、个性化。企业为满足消费者的各种需求,物流配送的压力越来越大。因此,如何整合社会资源以提高物流作业效率,成为了企业物流信息化建设的重要方向。
国内学者们从车辆调度问题、共同配送和需求分析3个方面对物流配送进行了研究。蹇洁等[1]构建了油耗费用和固定费用最小的车辆调度模型,并采用云自适应遗传算法进行求解。任伟[2]为优化带时间窗的车辆调度计算问题,引入量子进化算法,提出了一种混合量子免疫进化算法。邵丽丽[3]提出了利用蚁群算法优化遗传算法来解决物流车辆调度问题。刘华旭[4]对共同配送模式下电动汽车配送调度的优化问题,提出用蚁群算法进行求解。陈磊等[5]用混合算法构建了物流配送总成本最小的目标函数,得到配送时刻不断变化下的车辆调度方案。邝海山[6]将客户需求分析、共同配送与动态车辆调度问题相结合进行研究,提出采用共同配送模式来实现车辆调度方案的合理化。崔丽等[7]采用分配-节约启发式算法,寻找需求驱动下的城市配送车辆动态调度问题的满意解。Xu Zhoucong等[8]利用基于车辆实时数据的有序样本聚类方法对特征周期进行划分,采用最小的车辆数量和最低的总运营成本,建立车辆调度优化模型。
以上文献运用云自适应遗传算法、量子进化算法、蚁群算法等对共同配送的车辆调度问题进行研究,建立了相应模型,得出合理的优化方案。但是,学者们对带硬时间窗的共同配送车辆调度优化问题的研究还较少。针对带硬时间窗的共同配送车辆调度优化问题,本文提出Sweep算法和PMX算子相结合的遗传算法(hybrid genetic algorithm, HGA),并以长株潭城市群生鲜食品共同配送中心区域内的配送数据作为实验对象,验证了该算法能得到更优的共同配送车辆调度方案。
1 数学描述
带硬时间窗的共同配送车辆调度问题主要考虑的因素有服务及时性、物流成本等。本文先建立数学模型,再分析如何在车辆性能相同、服务时间不同的情况下,高效地完成配送任务。
1.1模型假设
假设:1)在现有备选点中,选取共同配送中心点,配送中心的固定成本记为常数;2)已知供应商的供货能力,且能针对客户的需求实现一对多的服务;3)不计配送中心的处理时间,采用最低成本运输方式来降低服务总成本。令ld为共同配送中心d的运量;F为供应商数;G为运输车辆数;lfg为车辆从供应商到共同配送中心的运量;Ld为所有供应商总的运量(见式(1));xd为备选点是否选为配送中心点(见式(2)) ;ycg为配送的时间是否有延误(见式(3))。

1.2模型表达
根据上述假设,模型的目标函数为总费用最小,
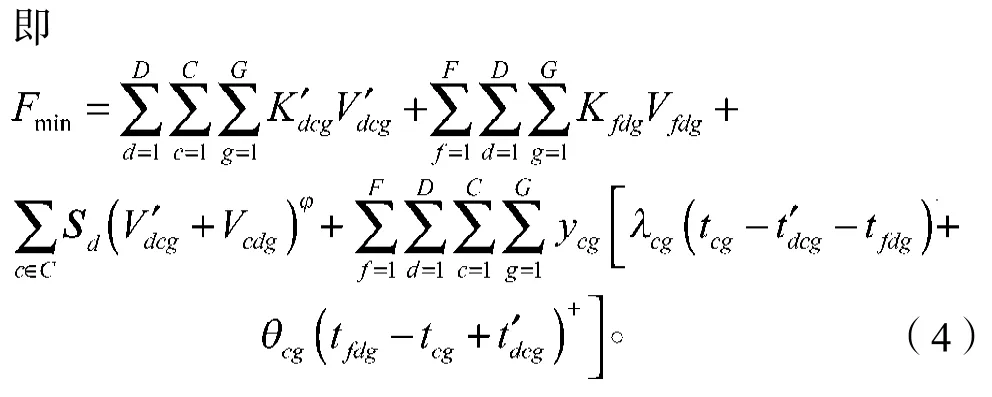
由式(4)可知,目标函数Fmin包含4个部分。
1)第一部分是配送中心到客户目的地所产生的物流费用。其中,D为共同配送中心数;C为客户数;为车辆从共同配送中心到客户的运输单价;为车辆从共同配送中心到客户的运输量。
2)第二部分是供应商到共同配送中心的运输费用。其中,Kfdg为车辆从供应商到共同配送中心的运输单价;Vfdg为车辆从供应商到共同配送中心的运输量。
3)第三部分是共同配送中心到客户的变动费用。其中,Sd为共同配送中心的货物流转单价;Vcdg为从客户返回共同配送中心的运输量;考虑到配送过程中会有意外损毁的情况,本文加入调节指数,且该指数满足条件0<≤1。
4)第四部分是车辆在时间窗范围内由配送服务产生的惩罚费用。由式(3)得,在客户“不允许延误”即ycg=1时,车辆没有在时间窗范围内完成客户的配送服务将产生惩罚值;当ycg=0时,就没有惩罚费用,即不存在延误情况。其中,Tcg为客户要求的车辆运输时间;cg为客户对车辆延时的惩罚(补偿)函数,即为车辆在时间窗范围外到达客户的惩罚值;cg为车辆在客户允许服务时间段之前到达而产生的惩罚函数,即为车辆在配送中心或客户时闲置或等待装卸而产生损失的机会成本;为车辆从共同配送中心到客户的运输用时;tfdg为车辆从供应商到共同配送中心的运输用时;“+”表示括号内结果为正时才有意义。
为了方便求解模型,需要对共同配送中心、供应商和客户的基本条件进行限定。
1) 每个共同配送中心的进出产品数量相同,

2)供应商的供应能力约束,即

式中Wfg为供应商供应车辆的能力。
3)时间约束,即
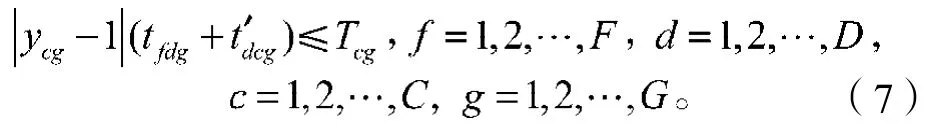
4)至少有一个共同配送中心被选中,

5)满足客户对产品数量需求的约束,

式中Q为共同配送中心的处理能力。
2 遗传算法设计
利用单一的遗传算法(genetic algorithm, GA)求解物流车辆调度问题,往往得不到最优解[9]。为弥补其不足,本文加入Sweep算法,构成组合遗传算法。该算法的具体步骤如下。
1)生成编码和初始种群。首先用整数序号表示客户点,问题的解集(即车辆路径的集合)用长度为N(N为有待接受服务的客户点数目)的整数数组进行编码,数组中相应的元素的顺序表示服务客户的顺序。在初始生成的随机编码中,取适当编码对应的路径组成初始群组,并令进化初值t=0,最大为T。
2)构造适应度函数。遗传算法的搜索过程只是以适应度函数为依据,运用种群的每个个体的适应度进行搜索。适应度函数用来判断个体的优劣,且成正相关性变动,即个体的适应度大,其性能优。适应度函数为

3)选择运算。选择运算是从种群中对个体进行优胜劣汰,根据适应度来确定再生个体。适应度比值法操作简单,容易实现,是最简单适用的选择方法。适应度比例函数为


4)交叉运算。采用PMX确定交叉算子,即先对父代进行常规的两点交叉,再根据交叉区域内各基因值之间的映射关系来修改交叉区域之外的各个基因组的基因值。挑选个体用于繁殖下一代时,互换选中的两个不同个体上的相同位置的基因,进而繁殖出新一代个体。
5)变异运算。本文采用实数编码的非一致性变异算子。令gr=(a1, a2,…, am, …)是第r代种群中的个体,选择浮点数am进行变异,则其变异结果为g′r=(a1, a2,…,, …),

6)当t大于最大进化代数时,终止遗传算法。
3 实验分析及算法比较
本文通过一个实例分析比较组合遗传算法、遗传算法、启发式算法,验证本算法的可行性和有效性。
3.1实验数据
本实验数据来源于长株潭城市群的生鲜食品配送中心及其供应商。该共同配送中心在不同时间段,为长株潭区域内106位客户提供服务,使用的运输车辆统一为载重20 t的车辆,车辆在各个客户处的服务时间均为调研统计所得,实验数据如表1所示。

表 1 实验数据表Table 1 Experimental data table
3.2算法比较
本文通过Matlab软件,将组合遗传算法、遗传算法、启发式算法3种算法分别对上述数据进行求解,并比较哪种算法得出的结果更优。
3.2.1组合遗传算法
组合遗传算法采用的数据容量是100,交叉率是0.77,变异率是0.06,迭代次数是310,稳态复制个体为4%,交叉算子用PMX。该算法的计算结果见表2。

表2 组合遗传算法计算结果Table 2 Combined genetic algorithm with its calculation results
由表2可知,由组合遗传算法得出平均路程为507.6 km,总平均成本为2 075.2元。9次平均迭代次数为234.1,效率较高。其中,9次运行中第6次的总成本最少,总成本为1 696元。根据第6次结果,由配送中心对106位客户进行带时间窗的定位,其运输路径安排如表 3所示,车辆数目为11,行驶路程为1 506.38 km,等待时间为644 min。表3中,每一行代表一辆车的行驶时间,如第一行是第一辆车到达每个客户(客户编号用1, 2,…,12表示)花费的时间,第一行第一列表示1号车从出发点到第一个客户花费的时间,第一行第二列表示1号车从第一个客户到第二个客户所花时间,以此类推。

表 3 路径安排表Table 3 Vehicle scheduling arrangement table
3.2.2遗传算法
遗传算法采用的数据容量100,迭代次数是310,交叉算子是0.8,变异算子是0.3。求解结果见表4。由表可知,第7次总成本最少,总成本为2 048元。

表 4 遗传运算Table 4 Calculations of the genetic algorithm
3.2.3启发式算法

表 5 启发式运算结果Table 5 Calculation results of the heuristic algorithm
3.2.4算法比较分析
将上述3种算法得出的结果进行比较,如表6所示。组合遗传算法(HGA)相比单独用遗传算法(GA)和启发式算法(HA),其结果的各项指标都占有优势。
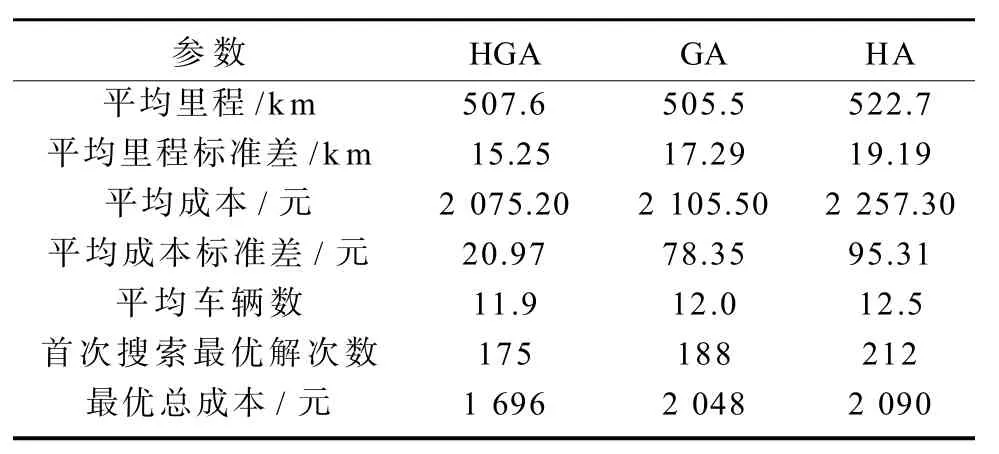
表 6 算法比较Table 6 A comparison between algorithms
4 结语
为了满足客户个性化和多样化的需求,针对带硬时间窗的共同配送车辆调度优化问题,本文设计了基于Sweep算法和PMX算子的组合遗传算法。通过选择编码、设计适应度函数、选取交叉算子,完成组合遗传算法设计。最后将3种算法进行比较分析,结果表明:组合遗传算法相比启发式算法和遗传算法性能更稳定,能得到更优的共同配送车辆调度方案。
[1]蹇洁,王旭,葛显龙. 云自适应遗传算法有能力约束的车辆调度优化[J]. 重庆大学学报,2013,36(8) :40-46. JIAN Jie,WANG Xu,GE Xianlong. Research on Capacitated Vehicle Routing Problem with Cloud Adaptive Genetic Algorithm[J]. Journal of Chongqing University,2013,36(8) :40-46.
[2]任伟. 基于量子免疫算法的车辆调度问题优化[J]. 计算机科学,2013,40(5) :233-236,270. REN Wei. Optimization Algorithm for Vehicle Scheduling Problem Based on Quantum Immune[J]. Computer Science,2013,40(5) :233-236,270.
[3]邵丽丽. 蚁群优化自适应遗传算法物流车辆调度实现[J].计算机测量与控制,2012,20(5) :1423-1425,1441. SHAO Lili. Ant Colony Optimization Adaptive Gene Algorism Resolving Logistics Vehicle Schedule[J]. Computer Measurement and Control,2012,20(5) :1423-1425,1441.
[4]刘华旭. 基于电动汽车技术特征的共同配送调度优化研究[D]. 北京:北京交通大学,2012. LIU Huaxu. Research on Scheduling Optimization of Common Based on Electric Vehicle Technical Feature[J]. Beijing:Beijing Jiaotong University,2012.
[5]陈 磊,霍永亮,霍波陶. 基于混合遗传算法的物流车辆调度优化[J]. 重庆师范大学学报(自然科学版),2015,32(2) :7-12. CHEN Lei,HUO Yongliang,Huo Botao. Vehicle Schedule Optimization of Logistics Based on Combinational Genetic Algorithm[J]. Journal of Chongqing Normal University(Natural Science),2015,32(2) :7-12.
[6]邝海山. 网购环境下城市共同配送动态车辆调度优化研究[D]. 重庆:重庆大学,2014. KUANG Haishan. Research on Dynamic Vehicle Scheduling Optimization for Urban Joint Distribution Under Online Shopping Background[J]. Chongqing:Chongqing University,2014.
[7]崔丽,王笑丛. 需求驱动下的城市配送车辆动态调度研究[J]. 计算机工程与应用,2015,51(2) :241-244. CUI Li,WANG Xiaocong. Demand-Driven Dynamic Configuration of Vehicle on City Distribution[J]. Computer Engineering and Applications,2015,51(2) :241-244.
[8]XU Zhoucong,HE Peijia,TENG Jing,et al. Transit Vehicles Intelligent Scheduling Optimization Based on the Division of Characteristic Periods[J]. Procedia-Social and Behavioral Sciences,2013,96 :1502-1512.
[9]欧卫华,唐东黎,闻斌. 基于遗传算法优化的模糊神经网络车型识别[J]. 湖南工业大学学报,2010,24(2) :39-42. OU Weihua,TANG Dongli,WEN Bin. Based on the Genetic Algorithm to Optimize the Fuzzy Neural Network Model Recognition[J]. Journal of Hunan University of Technology,2010,24(2) :39-42.
(责任编辑:邓彬)
On the Joint Distribution Vehicle Scheduling with Hard Time Windows
BIN Hou,WANG Jin
(Business School,Hunan University of Technology,Zhuzhou Hunan 412007,China)
A genetic algorithm, with the sweep algorithm combined with PMX operators, has been introduced to solve the problem of the joint distribution vehicle scheduling with hard time windows. With the distribution data of fresh produce joint distribution center in the Greater Changsha Metropolitan Region a test subject, the genetic algorithm has been introduced to make an analysis of a proper vehicle routing arranged for the clients, with a minimum total distribution cost, according to their deadline requirements. The result of a comparison made between this algorithm, the heuristic algorithm and the genetic algorithm shows that this algorithm provides a better solution to the joint distribution vehicle scheduling.
hard time window ;joint distribution ;vehicle scheduling
U492.2+2
A
1673-9833(2016)03-0086-05
10.3969/j.issn.1673-9833.2016.03.016
2015-12-25
湖南省哲学社会科学基金资助项目(14YBA133)
宾厚(1974-),男,湖南株洲人,湖南工业大学副教授,博士,主要研究方向为城市共同配送,E-mail:1173260751@qq.com
王缙(1991-),男,湖南益阳人,湖南工业大学硕士生,主要研究方向为城市共同配送,E-mail:871661468@qq.com

