可数离散交换群作用下极小系统测度敏感性
余林清
(合肥工业大学数学学院,合肥230009)
可数离散交换群作用下极小系统测度敏感性
余林清
(合肥工业大学数学学院,合肥230009)
研究了可数离散交换群作用的测度敏感性,并研究了相关性质.并且对一个极小系统,我们给出了测度n-敏感但不是(n+1)-敏感的系统的结构的一个刻画.
极小性; 测度敏感性; 局部proximal关系
1 引 言
自1986年Devaney定义Devaney混沌以来,初值敏感性作为定义该混沌的核心内容一直受到广泛研究.在文献[2]中,Akin和Kolyada给出了一个比初值敏感性更强的概念,即Li-Yorke敏感,并且证明了任何一个弱混合系统一定是Li-Yorke敏感的.2005年,熊金城[11]引入n-敏感性的概念.之后,邵松,叶向东和张瑞丰[7]研究了极小拓扑动力系统中关于n-敏感性的一些性质.2008年,叶向东和张瑞丰[4]引入敏感集的概念并且证明了一个传递系统是敏感的当且仅当存在一个元素个数大于等于2的敏感集.
由于拓扑动力系统和遍历论之间有着紧密的联系性,人们自然地想到将敏感性的概念引入到遍历论中.2005年,Cadre和Jacob[10]对于可测动力系统给出了逐对敏感性的概念并证明了一个弱混合的可测动力系统是逐对敏感的.随后,James, Koberda, Lindsey, Silva和Speh[12]对此问题做了进一步研究,给出了可测敏感性的概念.黄文,鲁平和叶向东[3]定义了μ-敏感性和μ-等度连续性等概念,得出μ-敏感性与逐对敏感性是等价的,同时证明了对于遍历的测度μ而言,μ-等度连续和非μ-敏感性等价.
本文受文献[3]启发,将整数加群作用下动力系统的测度敏感性推广到一般可数离散交换群作用,主要对测度敏感的极小系统的结构进行了一个刻画.
2 准备知识
Δn(X)={(x,x,…,x)∈Xn∶x∈X}.
设X是一个紧致的Hausdorff空间,G为离散拓扑群.如果φ∶G×X→X连续且满足
(i)对任意x∈X,有φ(e,x)=x,其中e是G的单位元;
(ii)对任意x∈X和g1,g2∈G,有φ(g1,φ(g2,x))=φ(g1g2,x),
那么称(X,G,φ)是一个拓扑动力系统(简记为TDS).为了方便起见,通常直接用(X,G)表示TDS,将φ(g,x)记为gx.在本文中,G取可数离散abelian群.
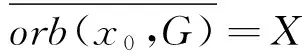
π(gx)=g(πx),∀g∈G,x∈X1,
那么称(X1,G)是(X2,G)的一个扩充或(X2,G)是(X1,G)的一个因子.系统(X,G)称为等度连续的是指对任意ε>0,存在δ>0,使得当d(x1,x2)<δ时,d(gx1,gx2)<ε,∀g∈G成立.
设(X,B,μ,G)是一个概率空间,B是X的一个σ-代数.如果对任意g∈G和B∈B,都有g-1B∈B且μ(g-1B)=μ(B),那么称(X,B,μ,G)是一个保测系统.记B+={B∈B∶μ(B)>0},M(X)为B上全体概率测度,M(X,G)为全体不变Borel概率测度.对μ∈M(X,G),定义μ的支撑为supp(μ)={x∈X∶对x的任意邻域U,μ(U)>0}.对于一个极小系统,有
命题2.1若(X,G)是一个极小系统且μ∈M(X,G),则supp(μ)=X.
证显然supp(μ)⊂X.下证X⊂supp(μ).对任意x∈X,设U是x的任意邻域.令E=X∪g∈Gg-1U,易知E是X的不变子集.由极小性可知E=∅.又因为X是紧致的,所以存在一个有限子集F⊂G,使得∪g∈Fg-1U=X,则有
因此,μ(U)>0,于是对任意x∈X,有x∈supp(μ),即X⊂supp(μ).
定义2.1设(X,G)是一个TDS且测度μ∈M(X,G).如果存在ε>0,使得对任意B∈B+,都能找到x,y∈B和g∈G,满足d(gx,gy)>ε,那么称(X,G)相对于测度μ是敏感的(或μ-敏感的).
类似地,将其推广到n情形.
定义2.2设(X,G)是一个TDS且测度μ∈M(X,G).如果存在ε>0,使得对任意B∈B+,都能找到x1,x2,…xn∈B和g∈G,满足d(gxi,gxj)>ε(其中1≤i 定义2.3设(X,G)是一个TDS且测度 μ∈M(X,G),xi∈X(i=1,2,…), 有以下结论. 结论2.1设π是动力系统(X,G)到(Y,G)的一个因子映射,测度μ∈M(X,G)且ν=πμ.若K是X的一个μ-敏感集且|π(K)|≥2,则π(K)是Y的一个ν-敏感集. 若点对(x,y)是proximal的,有时也称xproximal于y.记P(X,G)为X的所有proximal对构成的集合. 将proximal关系进一步推广,我们定义局部proximal关系. 记Qn(X,G)为X的全体n-局部proximal串构成的集合.特别地,当n=2时,记Q(X,G)=Q2(X,G).由定义易知,一个系统(X,G)是等度连续的当且仅当Q(X,G)=Δ2(X). 定义3.3设(X,B,μ,G)是一个保测系统且F⊂G.如果对任意B∈B+,存在e≠f∈F(其中e为单位元),使得μ(B∩f-1B)>0,那么就称F具有性质P. 令 P(x)={y∈X∶对y的任意邻域U,N(x,U)具有性质P }, 其中N(x,U)={g∈G∶gx∈U}. 下面命题给出了判定性质P一个方法. 命题 3.1设(X,B,μ,G)是一个保测系统,测度μ∈M(X,G)且F⊂G.如果对每一个N∈,存在B⊂G且,使得BB-1⊂F,那么F具有性质P. μ(∪s∈Ss-1(A))=Nμ(A)>1, 给定一个动力系统,下面命题有助于我们找到一个相对于测度而言的n-敏感串. 命题3.2若(X,G)是一个传递系统,测度μ∈M(X,G)且μ(TranG)=1.则有 (ii) 设Ui为xi的任意邻域,其中i=1,2,…,n+1.不失一般性,设xn+1∈P(x1),于是对任意A∈B+,存在g∈N(x1,Un+1),使得μ(A∩g-1A)>0.令V=U1∩g-1Un+1,易知V为x1的邻域.因此,存在y1,y2,…,yn∈A∩g-1A和h∈G,使得hy1∈V且hyi∈Ui,其中i=2,3,…,n.令zi=yi(i=1,2,…,n)且zn+1=gy1,则有z1,z2,…,zn+1∈A.所以 hz1∈V⊆U1,hzi∈Ui(i=2,3,…,n) 且 hzn+1=(hg)y1=gh(y1)∈gV⊆Un+1. 设F⊂G,如果存在一个动力系统(X,G),且x∈X和极小点y∈X以及y的一个邻域U使得(x,y)∈P(X,G)且N(x,U)⊂F,那么称集合F为一个中心集. 文献[5]中,命题8.10证明了每一个中心集都包含一个IP集,那么将此结果推广到群上是否仍然成立?这便是接下来要讨论的内容. 首先给出群上IP集的定义,一个子集A⊂G称为IP集是指存在一个网{gn}⊂G,使得 A={gi1gi2…gik:i1 命题3.3每个中心集都包含一个IP集. 证设(X,G)是一个TDS且(x,y)∈P(X,G),y为极小点,U为y的任意邻域,则N(x,U)是一个中心集.首先说明存在p∈G,使得px∈U且py∈U.设y∈V⊂U,取ε>0,使得对任意z′∈V,当d(z,z′)<ε时,总有z∈U.令 (3.1) 其中F为G的有限子集.令δ>0,使得当d(x′,x″)<δ时,有d(bx′,bx″)<ε,∀b∈F.因为xproximal于y,所以存在{gn}⊂G,使得infd(gnx,gny)→0.于是存在a∈{gn},使得d(ax,ay)<δ.从而 d(b(ax),b(ay))=d(abx,aby)<ε. 由式(3.1)可知,存在某些b∈F,满足(ab)y∈V,则有(ab)x∈U.所以存在p=ab∈G,使得px,py∈U. pkx,pky∈Uk,Uk+1⊂Uk,pkUk+1⊂Uk. pi1pi2…pirx∈pi1pi2…pir-1Uir⊂pi1pi2…pir-2Uir-1⊂…⊂pi1Ui2⊂Ui1⊂U1. 所以pi1pi2…pir∈N(x,U).于是N(x,U)包含一个IP集. 下面引理是文献[6]中定理1.2的另一种表述. 在这一节,给出测度敏感的极小系统结构的一个刻画.为此,需要先证明下面一个引理. 引理4.1若(X,G)是一个极小系统,则(x,y)∈Q(X,G)的一个充要条件是y∈P(x). 证充分性.设y∈P(x)且测度μ∈M(X,G).对任意ε>0,令U1=B(x,ε/2),U2=B(y,ε/2).由命题2.1可知,X=supp(μ),则μ(U2)>0.由于y∈P(x),所以N(x2,U)具有性质P.于是存在g∈N(x2,U),使得μ(U2∩g-1U2)>0.取x′=x和y′∈U2∩g-1U2,则 d(x,x′)<ε,d(y,y′)<ε 且d(gx′,gy′)<ε.故(x,y)∈Q(X,G). (4.1) 接下来证明N(x,U)具有性质P. 接下来便是本文主要结果. 定理4.1设(X,G)是一个极小系统,(Y,G)是它的极大等度连续因子,π为因子映射且测度μ∈M(X,G),ν∈M(Y,G).则 (i) 若K是X的μ-敏感集,则对某些y∈Y,有K⊂π-1y. (iii) (X,G)相对于测度μ是n-敏感但不是(n+1)-敏感的一个充要条件是max{|π-1y|:y∈Y}=n(其中n≥2). (iv) (X,G)不是μ-敏感当且仅当(X,G)等度连续. Q(X,G)={(x,x′)∈X2:π(x)=π(x′)}. (iii)(充分性)由于max{|π-1y|:y∈Y}=n,则存在y0∈Y,使得|π-1y0|=n,于是由(ii),(X,G)相对于测度μ是n-敏感的,假设(X,G)相对于测度μ是(n+1)-敏感的,则存在一个μ-敏感集K且|K|=n+1,由(i),存在y1∈Y,使得K⊂π-1y1,于是|π-1y1|≥n+1,矛盾. (iv) 充分性.设(X,G)为等度连续的.由题设(Y,G)为它的极大等度连续因子,故对任意的y∈Y,|π-1y|=1.假设(X,G)是μ-敏感的,则存在μ-敏感集K使得|K|>1,由(i),存在y∈Y,使得K⊂π-1y,矛盾.故(X,G)不是μ-敏感的. 必要性.任取(x1,x2)∈Q(X,G),则有x1,x2∈π-1y.假设x1≠x2,由(ii)可知(X,G)是μ-敏感的,矛盾.所以Q(X,G)=Δ2(X),这表明(X,G)是等度连续的. 本文将整数加群作用下的测度敏感性推广到一般可数离散交换群作用,并且给出测度n-敏感但不是(n+1)-敏感的极小系统结构的一个刻画. [1]叶向东,黄文,邵松.拓扑动力系统概论[M].北京:科学出版社,2008. [2]Walters P. An Introduction to Ergodic[M]∥ Therry Graduate Texts in Mathematics, Vol. 79.New-York -Berlin: Springer-Verlag, 1982. [3]Huang W, Lu P and Ye X. Measure-theoretical Sensitivity and equicontinuity[J]. Israel Journal of Mathematics, 2011, 183: 233-283. [4]Ye X and Zhang R. On sensitive sets in topological dynamics[J]. Nonlinearity, 2008, 21: 1601-1620. [5]Furstenberg H. Recurrence in Ergodic Theory and Combinatorial Number Theory[M]. Pri nceton: Princeton University Press, 1981. [6]Veech W A. The equicontinuoud structure relation for minimal abelian transformation groups[J]. AmericanJournal of Mathematics, 1968, 90: 723-732. [7]Shao S, Ye X and Zhang R.. Sensitivity and regionally proximal relation in minimal system[J]. Science in China, 2008, Series A 15: 987-994. [8]Glasner E and Weiss B. Sensitive dependence on initial conditions[J]. Nonlinearity, 1993, 6: 1067-1075. [9]Akin E and Kolyada S. Li-Yorke sensitivity[J]. Nonlinearity, 2003, 16: 1421-1433. [10]Cadre B and Jacob P. On pairwise sensitivity[J]. Journal of Mathematical Analysis and Applications, 2005,309: 375- 382. [11]Xiong J C. Chaos in a topologically transitive system[J]. Science in China, 2005, Series A 48: 929-939. [12]James J, Koberda T, Lindsey K, Silva C E and Speh P. Measureable sensitivity[J]. Proceedings of the American M- athematical Society, 2008, 136: 3549-3559. On Measurable Sensitivity in Minimal System for Countable Discrete Abelian Group Action YULin-qing (Department of Mathematics, Hefei University of Technology, Hefei 230009, China) We introduce the notion of measurable sensitivity for countable discreter abelian group action and study some of its properties. For minimal system, we give a characterization of a minimal system which is measurable n-sensitive but not(n+1)-sensitive. minimality; measurable sensitivity; regional proximal relation 2015-12-11;[修改日期] 2016-03-08 国家自然科学基金(11001071,11171320)及中央高校基本科研业务费(2015HGZX0017) 余林清(1990-),男,合肥工业大学硕士研究生,从事动力系统研究. Email: yulinqing90@163.com O189.11 A 1672-1454(2016)03-0049-06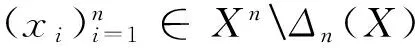
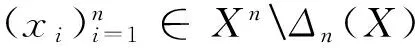
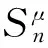
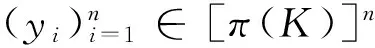
3 局部proximal关系
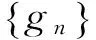
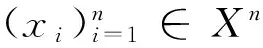
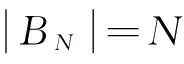
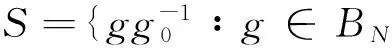
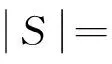
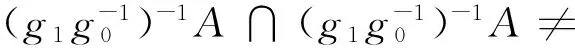
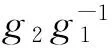
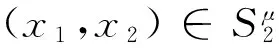

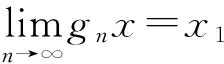
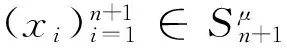
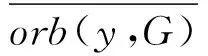
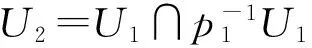
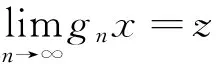
4 主要结果及证明
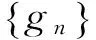
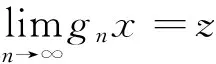
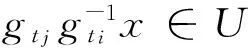
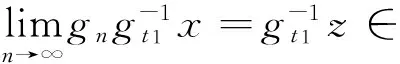
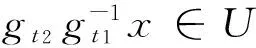
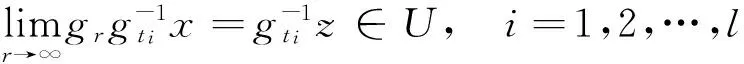
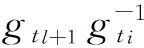
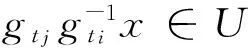
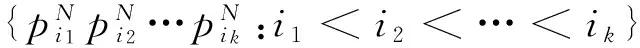
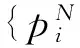
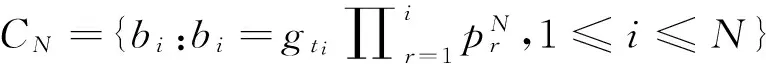
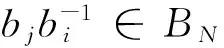
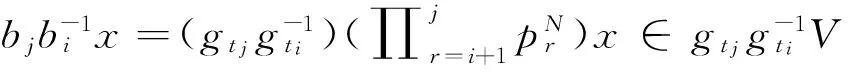
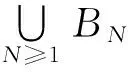
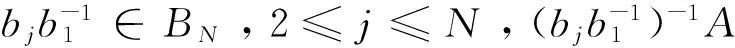
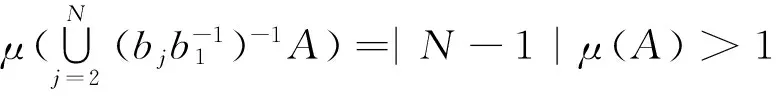
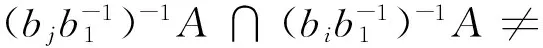
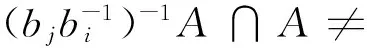
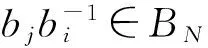
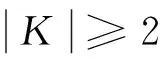
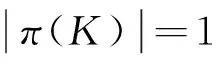
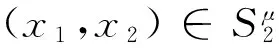
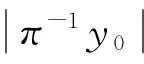
5 结 论

