一类具有一般发生率的阶段结构传染病模型的稳定性

程晓云， 胡志兴

(1.西安培华学院通识教育中心，西安710065；　2.西北大学数学学院，西安710069；3. 北京科技大学 数理学院，北京 100083)



一类具有一般发生率的阶段结构传染病模型的稳定性

程晓云1,2， 胡志兴3

(1.西安培华学院通识教育中心，西安710065；2.西北大学数学学院，西安710069；3. 北京科技大学 数理学院，北京 100083)

建立了一类具有一般发生率的阶段结构传染病模型，利用Hurwitz判据和极限系统理论知识等，分别讨论了染病者无输入和染病者有输入时，疾病消除平衡点和地方病平衡点的局部和全局稳定性，得到了一些重要结论，并对所得结果进行了数值模拟.

传染病模型； 平衡点； 局部渐近稳定； 全局渐近稳定

1　引　　言

2　模型的建立

本文考虑种群具有迁入且具有一般接触率β(N)的幼年患病的传染病模型，疾病的传播机制如下：

图1　疾病的传播机制

对应的传染病模型为

(1)

该模型参数除α为非负数外，其余均为正.其中种群总数为N=S+I+y，S，I，y分别表示t时刻幼年易感种群、幼年染病种群及成年种群的数量，A为外界迁入的种群数量，a，b，c表示种群各类的迁入比例，a+b+c=1.k表示单位时间内幼年成长为成年的转化率，β(N)表示疾病的传染率，γ表示疾病的恢复率，d，α分别表示自然死亡率和因病死亡率.该模型的特点是病人康复后不具有免疫力，马上又被感染，一般适用于通过细菌传染的疾病.假设

(2)

将S=N-I-y代入系统(1)，则系统(1)等价于下面的系统

(3)

2　染病者无输入时系统的稳定性

此时在系统(3)中，b=0.系统(3)变为

(4)

2.1系统的解的性态及平衡点的存在性

定理1对系统(4)，以下结论成立

(i) 若初始条件I(0)=0，则对任意的t>0，恒有I(t)=0，且

(ii) 若I(0)>0，则对任意的t>0，恒有I(t)>0，且系统(4)的正不变集为

(5)

证(i)根据解的存在唯一性，易知当I(0)=0.则对任意的t>0，恒有I(t)=0.此时系统(4)的第三个方程变为

N′=A-dN.

不难求得

又由(4)的第二个方程，将N与y看作已知量，可求得y(t)满足初始条件y(0)=y0的解为

当t→∞时，对上式两端取极限，即可证明

由系统(4)的第三个方程得

N′(t)=A-dN-αI≤A-dN.

根据比较定理，可求得

定理2对系统(4)，以下结论成立

(ii) 令

N*是方程

(ii)若I≠0，系统(4)的地方病平衡点由以下方程组

(6)

确定.

由(6)后两个方程可得

代入到(6)第一个方程，得

(7)

令

则

由R0>1得

故

(8)

又

由(2)知

(9)

2.2平衡点的局部稳定性

定理3对(4)的平衡点进行分析，可得如下结论

矩阵J(E0)的特征方程的特征根为

故当R0<1时，局部渐近稳定；当R0>1时，不稳定；当R0=1时，稳定性不能确定.

由于

故J(E*)可化简为

定义矩阵

2.3无因病死亡时平衡点的全局稳定性

此时α=0，系统(4)变为系统

(10)

系统(10)的正不变集为(8).

设

不难求得系统(10)有两个平衡点

定理5对系统(10)的平衡点进行分析，可得如下结论：

(11)

系统(11)的正不变集为

(12)

由(11)的第二个方程，可求得

把此极限值代入到系统(11)的第一个方程，得如下极限系统

(13)

系统(13)的正不变集

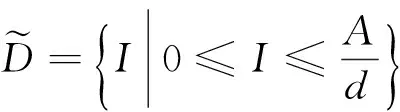
(14)

3　染病者有输入时系统的稳定性

此时b≠0，在正不变集D上对系统(3)进行讨论.

3.1系统的平衡点及其存在性

N*是方程

证系统(3)无无病平衡点是很显然的，而地方病平衡点由方程组

(15)

确定.

由系统(3)后两个方程，得

代入到(3)第一个方程，得

(16)

令

类似定理2的证明，我们知道p′(N)≥0，且当N→0时，p(N)<0.即可找到一个任意小的小正数ε>0，使得p(ε)<0；又q′(N)>0，且q(0)>0，故q(ε)>q(0)>0.从而有

F(ε)=p(ε)-q(ε)<0.

3.2无因病死亡时平衡点的全局稳定性

讨论α=0时，地方病平衡点的全局稳定性.此时系统(3)变为

(17)

系统(17)的正不变集为(5).

系统(17)的正平衡点由方程组

(18)

求得.

由(18)的后两个方程得

代入(18)第一个方程，并注意到I≠0，可得

(19)

根的判别式

令

方程(19)有两个实数根

证与定理3的证明类似.

定理8当α=0时，地方病平衡点E**在区域D上全局渐近稳定，此时疾病将蔓延为地方病而不会消除.

将这两个极限值再代入系统(17)的第一个方程，化简整理得

显然，当I>I**时，I′<0，即函数I(t)单调递减；当00，函数单调递增，从而地方病平衡点I=I**全局渐近稳定.同定理4，利用引理4及极限系统理论即可证明.

4　数值模拟

情形1：b=0，取a=0.6,c=0.4.

(i) 当α=0,β=0.5时，满足定理5中(i)的条件，则计算机模拟的系统(10)的轨线的相图如下：

图2　b=0,A=40,d=0.01,γ=0.02,k=0.05,a=0.6,c=0.4,α=0,β=0.5时，系统(10)的相图

从图2可以看出，无病平衡点是稳定的.即满足不同初始值的轨线最终趋向于无病平衡点，从而疾病最终消除.

从图3可以看出，正平衡点是稳定的.即系统(10)从不同初值出发的轨线最终趋于这一点，传染病最终不会消除而成为地方病长期存在.

图3　b=0，A=40，d=0.01，γ=0.02，k=0.05，a=0.6，c=0.4，α=0，β=0.9时，系统(10)的相图

情形2：b≠0，取a=0.6,b=0.1,c=0.3.

当α=0,β=0.5时，满足定理7的条件，则计算机模拟的系统(17)的相图如下：

图4　A=40,d=0.01,γ=0.02,k=0.05,a=0.6,b=0.1,c=0.3,α=0,β=0.5时，系统(17)的相图

从图4以看到，系统(17)的唯一地方病平衡点是稳定的，即从不同初值出发的轨线最终都趋向于地方病平衡点，此时疾病最终不会消除而成为地方病.

5　结　　论

本文分别研究了染病者无迁入和染病者有迁入且传染率为一般形式的幼年患病的传染病系统，由于考虑了种群的迁入及不是具体表达式的一般接触率，从而使研究的难度加大，所得结果不能尽善.但通过计算机模拟，作者猜测定理5可以完善为

(i)当R0<1时，系统(4)的无病平衡点全局渐近稳定；

(ii)系统(4)只要地方病平衡点存在即全局渐近稳定.定理8可以完善为：系统的地方病平衡点无条件存在且无条件全局稳定.这些情况是否成立还有待进一步研究.

[1]Wang Wendi，Chen Lansun.A pedator-prey system with stage-structure for predator[J].Computers & Mathematics with Applications，1997，33(8)： 82-91.

[2]Song Xinyu，Chen Lansun. Optimal harvesting and stability for a two-species competitive system with stage structure[J].Mathematical Biosciences，2001，70：173-186.

[3]Liu S， Chen L.Recent progress on stage-structured population dynamics[J]. Mathematical And Computer Modelling，2002，36(11-13)：319-1360.

[4]Gao Sujing. Optimal harvesting policy and stability in a stage structure single-species growth model with cannibalism[J]. 生物数学学报，2002， 17(2)： 194-200.

[5]Zeng Guangzhao，Sun Lihua. Permanence and existence of periodic solution of nonautomous predator-prey model with stage structure and delay[J].生物数学学报[J]，2005， 20(2)： 149-156.

[6]曹瑾，武佳，唐蕾，张双德. 具脉冲两阶段结构的自治SIS传染病模型[J]，大学数学，2009，27(5)：62-68.

[7]Xiao Yanni，Chen Lansun. Analysis of a three species eco-epidemiological model[J].Journal of Mathematical Analysis and Applications， 2001， 258： 733-754.

[8]Zhou Yicang.Stability of periodic solutions for an SIS model with pulse caccination[J].Mathematicaland Computer Modelling，2003，38：299-308.

[9]王翠姣，宋燕，王旭辉.一类具有垂直传染和预防接种的SEIR传染病模型[J].大学数学，2010，26(4)： 126-129.

[10]Zhao Xiaoqiang，Zou Xingfu. Threshold dynamics in a delayed SIS epidemic model[J].Journal of Mathematical Analysis and Applications， 2001，57： 82-291.

[11]Li Jianquan， Ma Zhien. Qualitative analyses of SIS epidemic model with vaccination and varying total population size[J].Mathematical and Computer Modelling，2002，35：1235-1243.

[12]Chen Junjie， Liu Xuangguan. Stability of an SEIS epidemic model with constant recruitment and a varying total population size[J]. Applied Mathematics-A Journal of Chinese Universities， 2006，21(1)：1-8.

[13]Dietz K.Overall population patterns in the transmission cycle of infectious disease agents[M]∥Anderson R M and May R M. Population biology of infectious diseases. Berlin: Springer Berlin Heidelberg, 1982: 87-102.

[14]Heesterbeek J A P， Metz J A J.The saturating contact rate in marriage and epidemic models[J].J.Math. Biol， 1993， 31：529-539.

[15]Zhang Juan， Li Jianquan，Ma Zhien. Global Analysis of SIR Epidemic Models with population size dependent contact rate[J].工程数学学报，2004， 2(21)：259-267.

[16]李健全，张娟，马知恩.一类带有一般接触率和常数输入的流行病模型的全局分析[J].应用数学和力学， 2004，25(4)：359-367.

[17]廖晓昕.稳定性的理论、方法和应用[M] .武汉：华中科技大学出版社，1999.

Stability of a Stage-Structured Epidemiological Model with General Incidence Rates

CHENGXiao-yun1,2,HUZhi-xing3

(1.Genera l Education Center, Xi’an Peihua University, Xi’an 710065, China;2. School of Mathematics, Northwest University, Xi’an 710069, China;3. School of Applied Science, Beijing University of Science and Technology, Beijing 100083, China)

The paper deals with a stage-structured edpidemological model with general incidence rates. By Hurwitz criterion and the theory of limiting systems, etc. When b=0 and b≠0 the local stability and the global stability of the disease free equilibriums and the epidemic equibriums are discussed, respectively. We get some important results and also simulate them.

epidemic model; equilibrium; local asymptotically stability; global asymptotically stability

2016-01-15；[修改日期]2016-04-19

国家自然科学基金(61174209)

程晓云(1978-)，女， 博士研究生， 讲师，从事生物数学及逻辑代数研究.Email：chengxiaoyun2004@163.com

O175.1

A

1672-1454(2016)03-0014-10