液压挖掘机动力总成悬置系统隔振性能分析与优化

廖瘦石，高永毅，蒋　勉，蒋玲莉

液压挖掘机动力总成悬置系统隔振性能分析与优化

廖瘦石1，2，高永毅3，蒋勉1，2，蒋玲莉1，2

（1.湖南科技大学 机械设备健康维护湖南省重点实验室，湖南 湘潭 411201；2.先进矿山装备教育部工程研究中心，湖南 湘潭 411201；3.湖南科技大学 物理与电子科学学院，湖南 湘潭 411201）

以某型国产液压挖掘机为研究对象，建立动力总成悬置系统数学模型与Adams动力学模型，仿真分析结果表明系统存在严重的耦合现象，隔振性能不理想。利用Isight软件集成Matlab，以悬置刚度参数作为设计变量，悬置系统能量解耦率为目标函数，以固有频率合理分配为约束条件，建立优化模型并开展灵敏度分析与优化分析，优化后系统解耦程度得到明显改善，优化方案对液压挖掘机动力总成悬置系统实车优化具有一定参考价值。

振动与波；液压挖掘机；动力总成悬置系统；能量解耦；优化分析

近年来，国产挖掘机的国内市场占有率不断提升，但在国际市场中的占有率不高，与国外产品相比，国产挖掘机在振动与噪声控制方面还存在较大差距。随着工程机械产品的竞争日益激烈，人们更多地考虑到产品的综合性能，对产品振动和噪声的指标控制也越来越严格［1-2］。动力总成产生的振动是挖掘机振动的主要来源之一，动力总成的振动如果不能被有效地隔离，就会传递到挖掘机的各个部位，引起共振，最后到达驾驶室位置，从而影响驾驶员的听力和舒适性。因此动力总成悬置系统的设计合理性直接关系到液压挖掘机整机的振动控制和使用性能以及操作舒适性［3-4］。

本文以某国产液压挖掘机动力总成悬置系统为对象，建立了动力总成悬置系统数学模型与动力学模型，运用Matlab和Adams软件进行仿真计算，验证了模型准确性，仿真分析了悬置系统的隔振性能，结果表明系统解耦程度较低，固有频率分布不合理。最后以悬置元件刚度为设计变量、固有频率的合理分配为约束条件，以系统解耦率为目标函数对悬置系统隔振性能进行优化，明显改善了系统的能量解耦程度。

1　动力总成悬置系统隔振性能分析

1.1悬置系统理论模型建立

建立动力总成悬置系统6自由度模型之前需要对相关结构进行简化，考虑到动力总成和车架的刚度远大于悬置系统刚度，一般将动力总成与车架视为刚体，橡胶悬置元件简化为三向正交的弹性阻尼元件，悬置元件质量忽略不计［5-6］。动力总成悬置系统的简化动力学模型如图1示，以动力总成质心位置为原点Go，x轴正向平行于曲轴中心线，且由发动机指向液压泵方向，y轴垂直于各气缸中心线所在平面，指向发动机右侧，z轴根据右手法则确定（垂直于气缸上端面，指向上方）。图中1—4分别代表悬置系统的四个悬置元件的位置，1、2分别为左前、右前悬置，3、4分别为左后、右后悬置［7-8］。

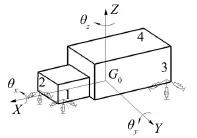
图1　动力总成悬置系统6自由度模型

通过拉格朗日法推导得到动力总成悬置系统的拉格朗日方程形式为

其中ET为系统动能；EV为系统势能；q为系统广义坐标；Q为系统所受广义力。

根据所建立的6自由度模型，分别求出系统总动能ET、总势能EV与总耗散能ED，再代入式（1）可得系统振动微分方程［9］为

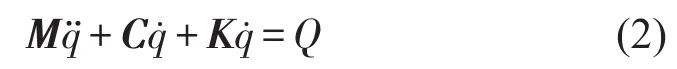
其中M为系统质量矩阵；C为系统阻尼矩阵；K为系统刚度矩阵；Q为系统所受广义力。

1.2悬置系统固有特性与能量解耦率

对动力总成悬置系统进行固有特性分析时，通常将振动系统简化为一个无阻尼的自由振动系统，则振动微分方程可简化为

式中A为系统自由振动时的振幅向量，A=（A1A2∙∙∙AN）T

将式（4）及其2阶导数代入式（1），得到主振型方程

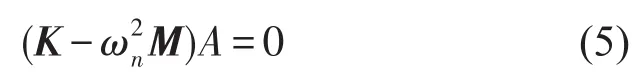
当系统做第i阶模态振动时，第k个广义坐标上分配的动能为［10］

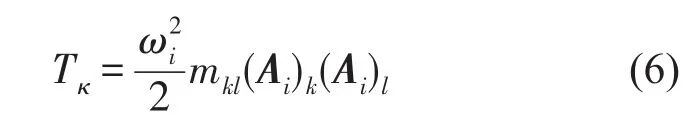
其中ωi为第i阶固有频率；Ai为系统第i阶主振型；（Ai）k，（Ak）l为Ai的第k个元素和第l个元素；mkl为系统质量矩阵第k行l列元素。

第k个广义坐标上分配到的动能所占系统总动能的百分比为

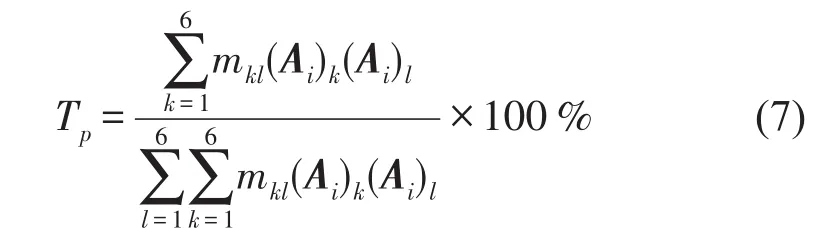
其中Tp反应各阶模态的耦合程度，若解耦率为100%，则表明系统第i阶的主振动的能量全部集中在第k个广义坐标上，在其他广义坐标方向的振动为零，从而实现了系统的完全解耦。

1.3Adams仿真模型建立

某型液压挖掘机动力总成部件由柴油发动机、液压泵组成，将其三维模型导入Adams软件，校正质量参数与质心坐标，发动机的四个悬置元件在Adams中用衬套力处理，忽略悬置元件的质量和扭转刚度、阻尼，通过在Adams中建立Maker点控制悬置元件的位置与方向，输入各主轴刚度参数，得到系统Adams模型如下图2示。

图2　动力总成悬置系统ADAMS模型

发动机为直列水冷六缸四冲程，主要激励为绕x轴方向的3阶质量扭矩Mx，将空间力系向质心坐标简化得动力总成激励力如下

式中Meo为发动机输出扭矩平均值。

动力总成的质量与转动惯量参数如表1所示，各悬置坐标、刚度参数如表2、表3所示。

表1　动力总成质量参数

表2　悬置位置坐标（单位/mm）

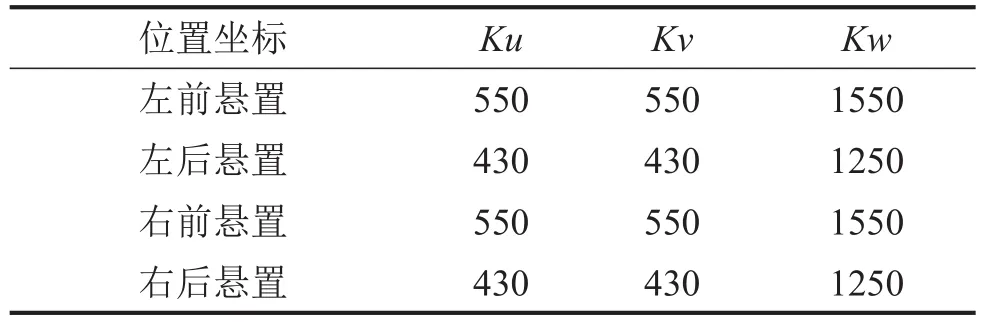
表3　优化前悬置刚度/（N/mm）

前悬置为斜置式安放，安装角度为45°，后悬置采用平置式安放。1.4仿真分析

通过在Adams中加载Vibration模块进行自由振动分析，同时用Matlab对式（3）、式（5）编程计算，得到悬置系统固有频率和能量解耦率，见表4和表5。

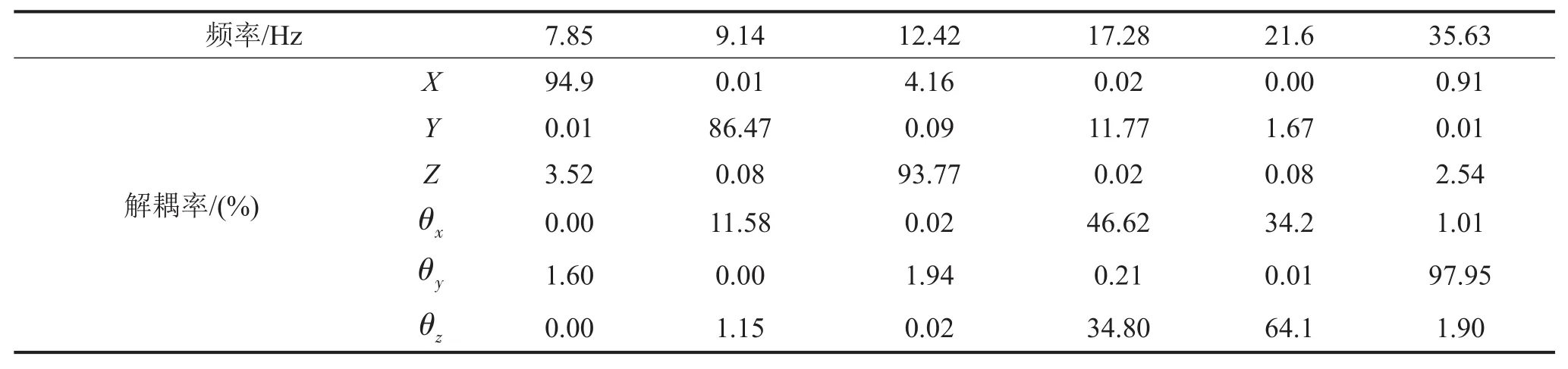
表4　Adams计算固有频率、能量解耦率

表5　Matlab计算固有频率、能量解耦率

将表4、表5中的参数对比可得，在Matlab编程计算的固有频率与Adams仿真结果误差很小，需要指出的是，能量解耦率在θx方向的误差较大。

考虑到Adams建模时简化处理，而Matlab考虑的是系统理想状态下的计算，上述误差在合理的范围内，可以认为Matlab数学模型计算结果与Adams仿真结果具有一致性，从而验证了Adams动力学模型的准确性。

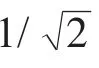
2　基于能量解耦的悬置系统优化分析

Isight是一款功能强大的计算机辅助优化平台，广泛应用于航空、航天、汽车、船舶等领域的零部件、子系统优化［12］。本文利用Isight提供的Matlab接口，调用了悬置系统的Matlab数学模型，通过拖拽优化组件（Optimization）建立了悬置系统的优化流程图，并设置好相关设计变量、约束条件、目标函数和优化算法，搭建了悬置系统优化模型。悬置系统优化流程图如图3所示。

图3　悬置系统优化流程图

2.1设计变量

发动机的参数与悬置位置与安装角度受实际生产限制，悬置阻尼主要作用是降低共振峰值，故选取四个悬置各主轴刚度作为设计变量［13］，共12个设计变量如下所示

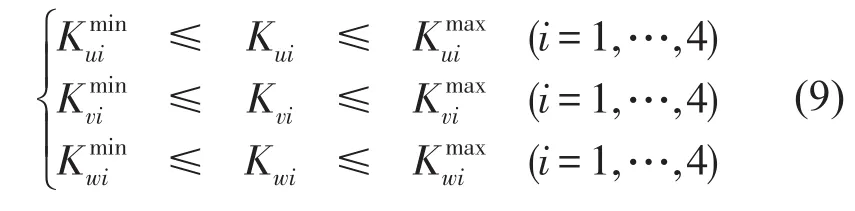
2.2目标函数

将悬置系统6个方向的最大解耦率设为目标函数如下

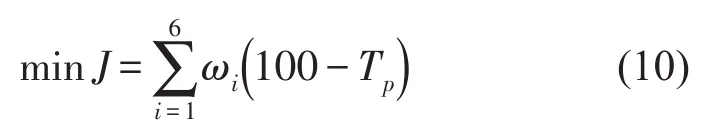
式中ωi为第i阶能量的加权因子，Tp为第i阶固有模态主要振动方向的能量百分比。

2.3约束条件

考虑到实际生产中，橡胶材料自身的压剪比一般在3～8之间［14］，因此建立其约束方程为

由于挖掘机工作环境较为恶劣，为了延长悬置寿命、避开路面激励频率，固有频率最小值应该大于5 Hz，由于人体的对垂直振动敏感的频率范围在4～6 Hz，系统的垂向固有频率应该避开这一范围［15-16］，根据隔振理论，悬置系统最高阶固有频率应小于35.35 Hz，各方向固有频率的约束范围如下。

表6　固有频率约束范围

2.4灵敏度分析

在优化设计之前，需要得到目标函数对设计变量的变化的灵敏程度，根据灵敏度分析结果进行针对性的优化设计。采用DOE分析，以12个设计变量为影响因子，系统耦合程度较低的θx、θz方向的解耦率作为响应，得到分析结果如图4、图5所示。

图4　各悬置刚度对θx方向解耦率的灵敏度

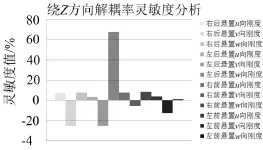
图5　各悬置刚度对θz方向解耦率的灵敏度

由上图可知各悬置主轴刚度对绕曲轴方向、绕z轴方向解耦率的影响程度，其中右前悬置v向刚度与做前悬置v向刚度对绕曲轴方向解耦率的影响程度最大，右后悬置v向刚度、左后悬置v向刚度、左后悬置w向刚度对绕z轴方向解耦率的影响程度最大。考虑到各设计变量均对解耦率有不同程度的影响，因此优化设计时取全部设计变量。

2.5优化结果

考虑到悬置系统优化模型中优化变量较多，因此选用NSGA-II算法［17］，NSGA-II算法是一种基于快速非劣性排序的改进型多目标遗传算法，其优点在于探索性能良好，算法参数设置如表7所示。在Isight中设置好设计变量、约束条件、目标函数后运行优化计算，得到目标变量的优化历程如图6所示。

表7　NSGA-II算法参数

图6　目标变量优化历程

Isight在优化过程中能直观地体现设计变量与目标函数的求解过程，直至获得满足约束条件的理想解，表8为优化后各悬置主轴刚度值，表9、表10分别表示优化前后悬置系统的固有频率与能量解耦率，分析可知，优化后系统固有频率均约束在合理范围之内，避开了发动机怠速激振频率，同时绕x轴与绕z轴方向的能量解耦率分别提高到94.98%与94.4%，其他模态方向的解耦率均在85%以上，优化后系统的解耦率得到大幅提高，满足了工程实际要求。

表8　优化后悬置刚度/（N/mm）

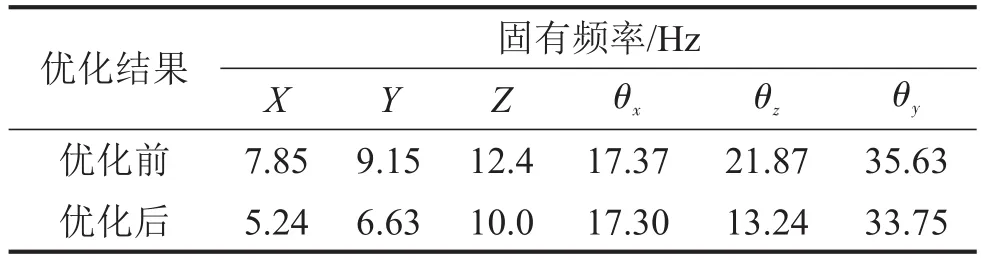
表9　优化前后悬置系统固有频率

表10　优化前后悬置系统能量解耦率

将优化后的悬置刚度进行振动仿真得到质心绕x轴角加速度与左前悬置z向加速度频域曲线如图7、图8所示，结果表明，优化后系统固有频率比优化前有了明显降低，系统固有频率避开了发动机怠速激振频率。

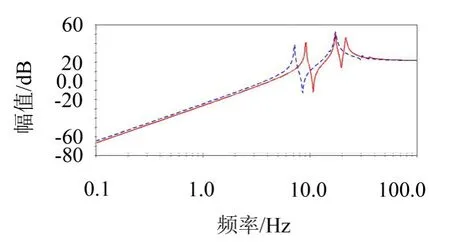
图7　质心绕x轴角加速度频域响应曲线

图8　左前悬置z向加速度频域响应曲线

3　结语

通过建立某型液压挖掘机动力总成悬置系统的数学模型和Adams仿真模型，在模型验证的基础上进行了仿真分析，仿真结果表明系统存在严重的耦合现象，系统隔振性能较差。利用优化软件Isight集成Matlab组件，以动力总成悬置系统6自由度解耦率为目标函数，以四个悬置元件各主轴刚度为设计变量，考虑固有频率的合理分配为约束条件，搭建了悬置系统优化模型，并进行优化分析，分析结果表明，优化后悬置系统固有频率的分布更为合理，避开了发动机激振频率，各方向的能量解耦率也得到大幅提升。优化结果满足工程实际要求，提出的优化方案对改善动力总成悬置系统隔振性能具有一定的实际指导价值。

［1］毛兴中.工程机械噪声控制技术［J］.筑路机械与施工机械化，2008，（4）：16-19.

［2］陈国俊.液压挖掘机（上、下册）［M］.武汉：华中科技大学出版社，2011.

［3］陈欠根，冯利花，过新华.挖掘机机动力总成悬置系统建模仿真研究［J］.合肥工业大学学报（自然科学版），2011，34（8）：1130-1134.

［4］刘丕晶，侯亮，黄伟.挖掘装载机动力总成悬置系统隔振性能仿真［J］.厦门大学学报（自然科学版），2012，51（6）：1005-1010.

［5］SEONHO C.Configuration and sizing design optimization of powertrain mounting system［J］.International Journal of Vehicle Design，2000，24（1）：35-47.

［6］吕振华，范让林.动力总成悬置系统振动解耦设计方法［J］.机械工程学报，2005，41（4）：49-54.

［7］陈欠根，过新华，彭勇，等.运用ADAMS的液压挖掘机动力总成悬置系统隔振性能仿真研究［J］.现代制造工程，2010（10）：61-64.

［8］李静.基于ADAMS/View与ISIGHT动力总成悬置系统仿真与优化［J］.农业装备与车辆工程，2014，52（7）：45-49.

［9］庄伟超，王良模，殷召平，等.基于遗传算法的混合动力汽车动力总成悬置系统的优化设计研究［J］.振动与冲击，2015，34（8）：209-213.

［10］孙蓓蓓，张启军，孙庆鸿，等.汽车发动机悬置系统解耦方法研究［J］.振动工程学报，1994，7（3）：240-245.

［11］王营.某挖掘机动力总成悬置系统隔振性能优化［J］.机械设计与制造，2015，21（5）：178-180.

［12］赖宇阳.ISIGHT参数优化理论与实例详解［M］.北京：北京航空航天大学出版社，2012.

［13］时培成.汽车动力总成悬置系统隔振分析与优化研究［D］.合肥：合肥工业大学，2010.

［14］胡倩，陈剑，沈忠亮，等.计及隔振率的发动机悬置系统稳健优化设计［J］.噪声与振动控制，2015，35（4）：78-84.

［15］伍建伟，刘夫云，李峤，等.基于遗传算法汽车动力总成悬置系统解耦优化［J］.噪声与振动控制，2015，35（5）：77-81.

［16］侯勇，赵涛.动力总成悬置系统解耦设计［J］.汽车工程，2007，29（12）：1094-1097.

［17］LYU N，SAITOU K，Decomposition-based assembly synthesis of a three-dimensional body-in-white model for structural stiffness［J］.Journal of Mechanical Design，2005，127（1）：34-48.

Analysis and Optimization for Vibration Isolation Performance of a Hydraulic Excavator's Powertrain Mounting System

LIAO Shou-shi1，2，GAO Yong-yi3，JIANGMian1，2，JIANG Ling-li1，2
（1.Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment，Hunan University of Science and Technology，Xiangtan 411201，Hunan China；2.Advanced Mining Equipment Engineering Research Center，Xiangtan 411201，Hunan China；3.School of Physics and Electronics，Hunan University of Science and Technology，Xiangtan 411201，Hunan China）

The mathematical model and the Adams dynamics model are established for the powertrain mounting system of a domestic hydraulic excavator.The simulation results show that there is a serious coupling phenomenon in the powertrain mounting system，and its vibration isolation performance is poor.Integrating Matlab with Isight software，an optimization model is constructed with the suspension stiffness parameters as the design variables and the energy decoupling as the objective function.Sensitivity analysis and optimization analysis are implemented with the constraints of rational allocation of natural frequencies.As a result，the decoupling situation of the system is significantly improved.This optimization method has valuable reference for real-vehicle optimization of the hydraulic excavator's powertrain mounting system.

vibration and wave；hydraulic excavators；powertrain mounting system；energy decoupling；optimization analysis

TU621；TK406

ADOI编码：10.3969/j.issn.1006-1335.2016.03.012

1006-1355（2016）03-0057-05+84

2015-12-07

国家科技支撑计划子资助项目（2015BAF07B03）；国家自然科学基金资助项目（51305133、51175172）

廖瘦石（1993-），湖南衡阳人，硕士研究生，主要研究方向为机械系统动力学及CAE分析。E-mail：liaoshoushiz@sina.com

蒋勉（1983-），男，湖南宁乡人，博士，讲师，主要从事复杂机械系统建模与优化及机械系统动力学研究。E-mail：jiangmian1983@aliyun.com