时变长度轴向移动绳横向受迫振动数值分析
杨 历,陈恩伟,吝辉辉,刘正士
时变长度轴向移动绳横向受迫振动数值分析
杨历,陈恩伟,吝辉辉,刘正士
(合肥工业大学 机械与汽车工程学院,合肥 230009)
分别建立移动集中载荷和移动分布式载荷作用下时变长度轴向移动绳系统的物理模型,基于Leibniz法和Hamilton原理推导具有时变参数的横向受迫振动方程,Galerkin法将其离散处理为一系列非线性常微分方程组,改进的四阶Runge-Kutta用于求解不同Galerkin截断阶数的非线性常微分方程组,同时分析基于有限元法求解系统运动方程及Newmark-β数值计算的移动集中载荷下变长度轴向移动绳系统横向振动特性。两种方法数值分析吻合性及收敛性表明建立变长绳移系统模型可靠性及求解时变参数系统方法有效性,同时变长度轴向移动绳系统在不同情况下采用恰当的Galerkin截断阶数能到达更好收敛性及保证计算精度。
振动与波;时变长度移动绳;Galerkin法;Newmark-β法;移动载荷;横向受迫振动
实际工程中很多设备都可简化为变长度轴向移动绳系统,如绳系卫星,电梯电缆,起重机缆绳等。在研究这些设备的横向振动时,不能简单地忽略各项外界因素的影响,尤其是外部载荷激励作用,因此研究外部载荷作用尤其是移动载荷作用下变长度轴向移动绳横向受迫振动[2-5]及其振动特性[8-12]对设备的设计及改造起到了很重要的作用。这类系统如移动风载荷作用下的起重机缆绳,安装有随动导轮的传输电缆,移动绳密度不均或磨损导致的质量不均系统等。M.Pakdemiri利用哈密顿原理及Galerkin法求解定长轴向加速移动绳横向振动,并利用Floquet原理分析其系统在不同条件下的稳定性[1]。Salih NAkour则在2010年分析了具有弹性支承的非线性梁在周期性分布载荷作用下的振动,应用哈密顿原理建立振动方程,对得到的拉格朗日方程离散化,最后使用龙格库塔法数值仿真[2]。M. Ansari同样利用哈密顿原理建立了欧拉-伯努利梁在非线性黏弹性基础下受移动载荷作用的振动响应,Galerkin将其离散,应用multiple-scales method获得不同条件下的内外共振和不同谐波下的频率响应[3]。Ye-Wei Zhang利用具有非线性特性的能量转移装置减小风载荷作用下轴向绳移系统的横向振动,牛顿第二定律用于建立振动方程,Galerkin法将其离散化,最后的数值分析结果证明了此能量转换装置对横向振动控制的有效性[4]。Ji-hu Bao对变长度柔性提升钢丝绳采用广义哈密顿原理导出其运动方程,将Galerkin离散后的数值仿真结果与实验进行对比,结果基本一致,证明数学模型的有效性,同时分析系统在外部周期性激励下的系统共振[5]。E. W.Chen等基于拉格朗日方程应用有限元离散法求解了定长及变长轴向绳移系统的非线性动力学方程,采用Newmark-β法及状态方程法数值分析系统频率及能量变化规律[6]。Qun Wu基于经典的Runge_Kutta方法,提出改进的Runge_Kutta方法的推导过程,并且基于改进的Runge_Kutta方法求解了定长及变长轴向移动绳系统的动力学响应[7]。本文基于以上研究,应用两种不同运动方程求解方法及不同数值分析方法,对比分析了两种方法在处理变长度移动绳受迫振动时的收敛性及精确性。
1 建模及运动方程求解
本文研究对象为时变长度轴向绳移系统,用以简化模拟实际工程应用中很多工程设备,图1所示为时变长度轴向绳移系统在受到移动集中载荷作用下的物理模型,图2所示为时变长度轴向绳移系统在受到移动分布载荷作用下的物理分解模型,其表示为求解宽度为a的移动分布载荷做功等于宽度为vt的移动分布载荷做功与宽度为vt-a的移动分布载荷做功之差。
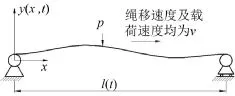
图1 移动集中载荷作用的时变长度轴向绳移系统物理模型

图2 移动分布载荷作用下的时变长度轴向绳移系统物理分解模型
图1中P为移动集中载荷,速度为v,p为单位长度载荷,a为移动分布载荷宽度,其速度为v。绳长为l(t),A为移动绳横截面积,ρ为单位长度密度,E为杨氏弹性模量,T0为移动绳的恒张力,v为移动绳轴向移动速度。x为绳上某点轴向位置的固定坐标轴,ẋ即为绳上点的移动速度,且̇=v。y(x,t)为绳上固定点在时刻t及位置x处的横向振动位移。物理模型的建立基于以下3个假设:移动绳具有连续和均匀性,且其线密度、横截面积、弹性模量、张力在运动过程中保持不变;忽略移动绳纵向振动影响,且移动绳的横向振动引起的弹性变形远小于绳长度;忽略移动绳受到的各种阻尼、摩擦力及气流影响。对绳系单元长度受力分析[13],系统的能量可得[6]:
系统的动能

系统的势能

图1中移动集中载荷做功

图2(a)中分布载荷做功为

图2(b)中分布载荷做功为

图2中分布载荷做功表示为

根据建模绳系两端固定支承,故其边界条件为

哈密顿原理有

将方程式(1)、式(2)、式(3)代入式(8)可得
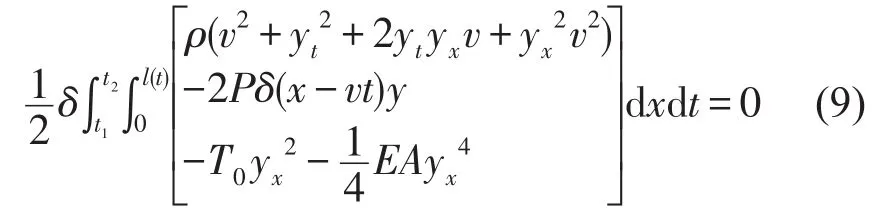
由上式可看出积分上限l(t)为时变函数,因此标准的分部积分法不能采用,此处应用Leibniz's和分部积分法相结合求解时变上限积分,且对上式中v 和y取变分可得

上式三项之和为零,即各项均为零,故移动集中载荷作用下时变长度轴向绳移系统横向振动方程为
需要控制好市政工程施工过程中出现的噪声。噪声污染对周围的居民生活会产生极大的影响,主要是市政工程施工过程中大型机械设备的噪声以及压路机作业等发出的声音。为了控制这些噪声污染,施工需要使用符合标准要求的设备,还要对施工设备进行定期维护。对施工现场的噪声进行监测,保证施工噪声不干扰附近居民,合理安排施工时间,避免在居民夜间休息时施工,施工时间尽可能选在白天,运输车辆需要低速行驶,禁止持续鸣笛,避免强噪声作业,在噪声敏感区域设置隔声屏,最大程度降低噪声。

同理移动分布载荷作用下时变长度轴向绳移系统横向振动方程为

2 运动方程离散化
应用Galerkin截断法将上述两个非线性偏微分方程离散化为常微分方程,因x在区间[0,l(t)]取值,故定义新变量ξ=x/l(t),其变化区间为[0,1]

其中qi(t),(i=1,2...n)为广义坐标,n为模数,形函数具有如下表示

对式(14)分别对时间及位移求偏导有

将式(16)到式(20)分别代入式(12)和式(13),并两边同时乘以φj(ξ)(j=1,2,3,…,n),并对ξ在[0,1]上积分,结合正交化关系可将方程离散为如下形式
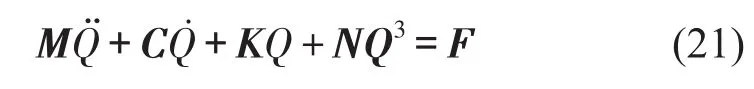
其中Q=[q1,q2…qn]T为广义坐标量,M、C、K及F分别为广义质量,阻尼,刚度及载荷矩阵,N为三次非线性项系数矩阵,这些矩阵每项分别表示为

3 数值仿真对比分析
在基于有限元法的Newmark-β法计算中[6],假设绳子具有固定单元数,且单元长度均相等,因此这种情况下移动集中载荷可以定义为载荷在每个单元节点上依次作用相等的时间,从而通过改变作用时间的大小即可模拟载荷不同的移动速度。每个单元节点上载荷作用时间步为

其中n1单元数,Dt每一步的时间长度,v为载荷移动速度,如取n1=30,Dt=0.02用以近似模拟移动集中载荷速度v=1 m/s。
3.1自由振动
初始条件设为

图3中线型为:—,Newmark-β法;—+,2阶Galerkin截断;—*,4阶Galerkin截断,横坐标为绳长,纵坐标为横向振动位移。图中表示不同时刻下,随绳长增加,绳系的横向振动特性,(a)中绳长逐渐伸长,系统最大振幅基本保持不变,而系统振动频率减小,经过相同时间,其振型相较于绳系缩短变化较小;(b)中绳长逐渐缩短,由于无阻尼存在系统最大振幅基本保持不变,系统振动频率增加,且其振型愈加复杂。三种方法在处理变长度移动绳系统横向自由振动时振型基本吻合,证明了Galerkin法的可靠性,且取2阶Galerkin截断处理时变自由度横向自由振动时就能达到较高的准确性及收敛性。

图3 变长度绳移系统不同速度下的横向自由振动
3.2移动集中载荷作用下的横向振动
轴向移动绳在移动集中载荷作用下,取二者移动速度均为1 m/s。结合工程实际,取集中载荷为正弦变化函数

其中A为载荷幅值,ω为载荷变化频率

如图4所示移动集中载荷幅值A=0.1 N,频率ω=0.3 Hz。—,Newmark-β法;—+,2阶Galerkin截断;—*,4阶Galerkin截断,可以看出绳中波在移动载荷作用下从绳左端产生,并且逐渐传播到右端,由于绳系右端固定,因此波传递到右端时会反射回来并传递到另一端,从而在绳中叠加成复杂的振动,同时由于移动载荷的不断做功,绳系振幅及振动频率亦逐渐增加。图4(a)、图4(b)中三种求解结果在振型上基本吻合,Newmark-β与Galerkin截断相对较大的误差主要来源于其载荷间断作用于不同节点,载荷不是连续作用于绳子上。并且由于变长度轴向移动绳系统的绳长是随时间逐渐伸长,而本文采用的是固定单元数的有限元离散化方法,即此时绳系单元长度是时变的,因此当绳长伸长长度较大时,单元的长度也会变化较大,从而结合本文中对于有限元方法下的集中载荷模拟原理,会导致计算精度下降,随时间推移形成较大误差。图4(c)、图(d)中明显可以得出4阶Galerkin截断与Newmark-β法具有更吻合的振型,因此在计算移动绳受到移动集中载荷作用下时至少4阶Galerkin截断才能取得较好的收敛性,同时可以看出Galerkin截断在处理受到移动载荷作用的绳移系统横向振动的有效性,同时证明了改进的4阶Runge_Kutta法在数值计算非线性常微分方程组时的可靠性。
3.3移动分布载荷作用下的横向振动
根据上面仿真分析结果,4阶Galerkin截断对于移动载荷作用下的轴向绳移系统横向振动具有较高的收敛性,能较准确地反映其横向振动,同时由于Newmark-β法在处理移动载荷时的局限性及较大误差,因此此部分采用4阶Galerkin截断结合改进的Runge_Kutta法数值仿真移动分布载荷作用下轴向绳移系统中点的横向振动。以下讨论参数取值为绳移速度v=1 m/s,ω=0.3 Hz,p=0.025 N/m,a=4 m,同时移动分布载荷形式与移动集中载荷相同,为正弦函数。
图5(a)所示为移动分布载荷幅值相同,单元长度载荷及宽度不同时绳移系统中点的横向振动,载荷宽度越大,中点振动初始幅值越大,振动响应越快,振动会随着载荷逐渐加载到绳子上而慢慢增加,同时P=0.1 N与p=0.8 N/m,a=0.125 m下的振型误差较小,在实际应用中,很多分布式载荷数学建模时可近似处理为移动集中载荷,从而减少运算难度。图5(b)所示为移动分布载荷移动速度分别为0.5 m/s、1 m/s、1.5 m/s时绳系统中点的振动,且绳移速度为1 m/s,载荷频率取0.3 Hz。由于分布载荷是逐渐加载到绳子上,故载荷速度越大绳子初始振幅越大,整体幅值也越大,但载荷移动速度对绳系振动频率没有明显影响,几乎不变。对应于实际工程应用中,通过选择合适的载荷移动速度大小,可以达到控制振动频率及振幅的目的。图5(c)为移动分布载荷频率分别为0.1 Hz、0.3 Hz、0.8 Hz时绳系中点的振动,绳及载荷移动速度均为1 m/s。由图可以很明显得出中点振动频率与移动载荷频率成正比,中点振幅与移动载荷频率成反比,即载荷频率逐渐增加,中点振动频率越大,中点振幅越小。
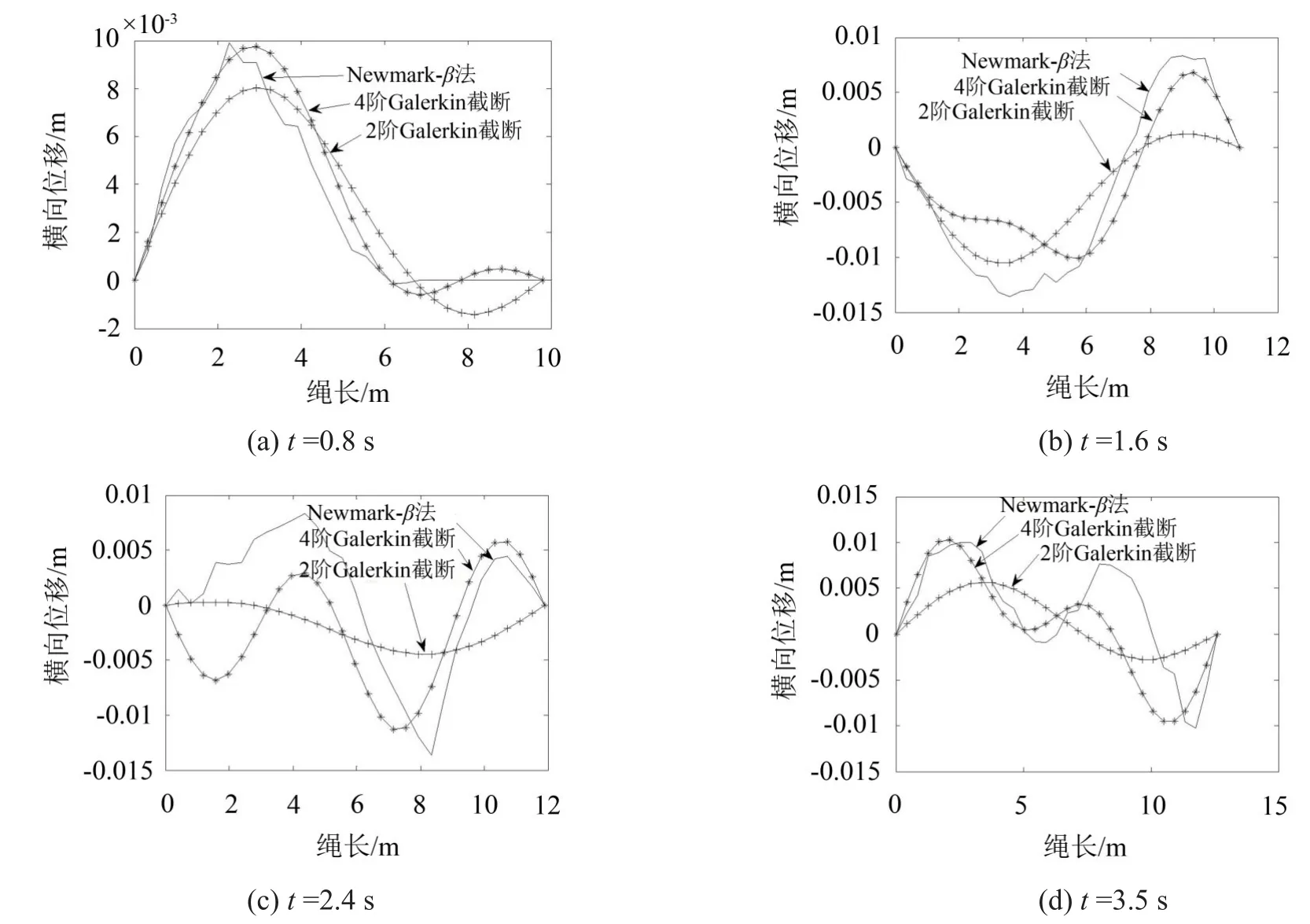
图4 移动集中载荷作用下的时变长绳移系统在不同时刻下的振型
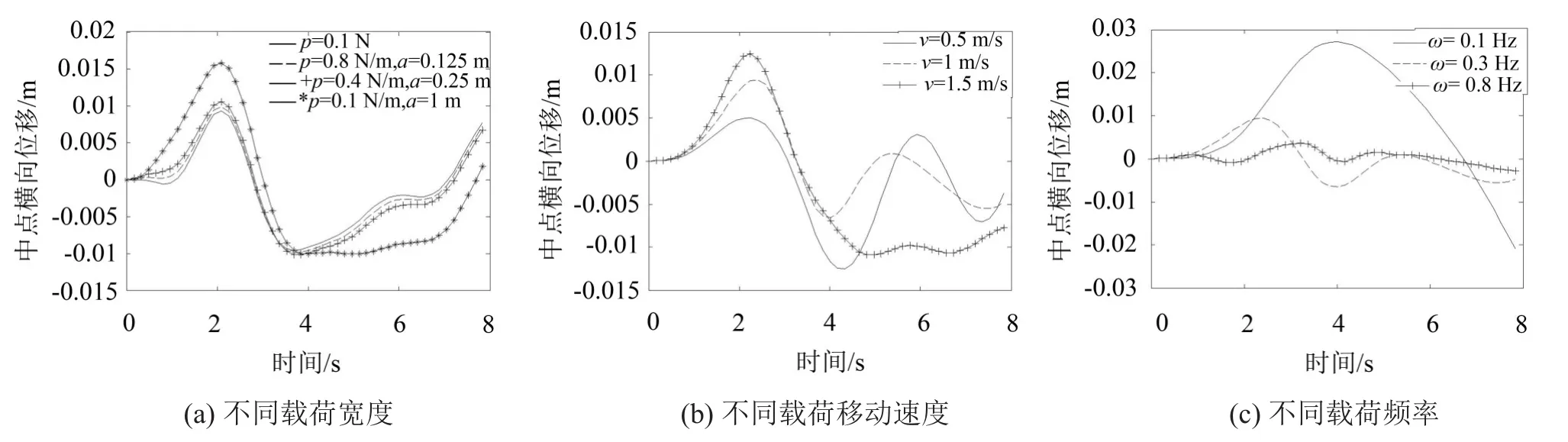
图5 不同参数下移动分布载荷作用的时变长绳移系统中点振动
4 结语
本文以时变长度轴向绳移系统为研究对象,分析了其在不同移动载荷作用下横向受迫振动,应用Leibniz法及Hamilton原理分别建立绳系在不同工况下的运动微分方程,同时应用Galerkin不同阶数的截断对微分方程离散化,数值计算结果与基于有限元离散的Newmark-β法进行比较,得出以下结论:
(1)通过三种方法对时变长度轴向绳移系统横向自由振动数值仿真对比,较高吻合度证明了Galerkin截断处理非线性偏微分方程的有效性,同时得出至少2阶Galerkin截断才有较好的近似模拟;
(2)时变长度轴向移动绳在受到移动载荷作用时,Newmark-β法和4阶Galerkin截断数值仿真结果具有较高的振型吻合度,可见这种情况下至少4阶Galerkin截断才有较好的近似值;
(3)研究了移动分布载荷作用下时变长度轴向绳移系统不同参数对振动特性的影响,同时分布载荷在一定程度上可以简化为集中载荷,因此分布载荷宽度对振动的影响可为进一步研究打下理论基础;
(4)实际工程应用中有各种类型的移动载荷,本文建立的移动载荷作用下的变轴向绳移系统理论模型及动态特性分析能为后续进一步研究更复杂载荷提供一定的理论基础,同时有助于时变长度轴向绳移系统的振动控制及进一步参数振动特性研究。
[1]PAKDEMIRI M.Transverse vibration of an axially accelerating string[J].Journal of Sound and Vibration,1994,169(2):179-196.
[2]SALIH N AKOUR.Dynamics of nonlinear beam on elastic foundation[C].Proceedings of the World Congress on Engineering,2010,978-988-18210-7-2:2078-0958.
[3]ANSARI M,ESMAILZADEH E,YOUNESIAN D. Internal-external resonance of beams on non-linear viscoelasticfoundationtraversedbymovingload[J]. Nonlinear Dynamics,2010(61):163-182.
[4]ZHANG YE-WEI,ZANG JIAN,YANG TIAN-ZHI,et al. Vibration suppression of an axially moving string with transverse wind loadings by a nonlinear energy sink[J]. Mathematical Problems in Engineering,2013,Article ID 348042,7 pages.
[5]BAO JI-HU,ZHANG PENG,ZHU CHANG-MING,et al. Transverse vibration of flexible hoisting rope with timevarying length[J].Journal of Mechanical Science and Technology,2014,28(2):457-466.
[6]CHEN E W,FERGUSON N S.Analysis of energy dissipation in an elastic moving string with a viscous damper at one end[J].Journal of Sound and Vibration,2014:2556-2570.
[7]WU QUN,CHEN E W.Modified Runge Kutta method for solving nonlinear vibration of axially travelling string system[C].The 21 st International Congress on Sound and Vibration,2014.
[8]袁宏智,马建敏.移动载荷作用下斜拉桥结构的动态响应计算分析[J].噪声与振动控制,2014,34(3):148-154.
[9]CZESŁAW I BAJER,BARTŁOMIEJ DYNIEWICZ. Space-time approach to numerical analysis of a string with a moving mass[J].International Journal for Numerical Methods in Engineering,2008(76):1528-1543.
[10]陈立群,吴俊.轴向运动黏弹性弦线的横向非线性动力学行为[J].工程力学,2005,22(4):48-51.
[11]陈立群.轴向运动弦线横向非线性振动研究的若干进展[C].第七届全国非线性动力学学术会议和第九届全国非线性振动学术会议论文集,2004.
[12]邵文韫,张国策,王志锋.高速轴向运动梁横向受迫振动的稳态分析[J].噪声与振动控制,2012,32(3):25-28.
[13]YAO C M,FUNG R F,TSENG C-R.Non-linear vibration analysis of a travelling string with time-dependent length by new hybrid Laplace transform/finite element method [J].Journal of Sound and Vibration,1999,219(2):323-337.
NumericalAnalysis of Transversely Forced Vibration for an Axially Travelling String with Time-Varying Length
YANGLi,CHEN En-wei,LIN Hui-hui,LIU Zheng-shi
(School of Mechanical andAutomotive Engineering,Hefei University of Technology,Hefei 230009,China)
The physical models of an axially travelling string system with time-varying length under the action of moving concentrated load and moving distributed load are established.Two kinds of moving forced string models are considered with different means.The nonlinear transversely forced vibration equations with time varying parameters of the string under different conditions are derived using the extended Hamilton's principle and Leibniz's rule,and discretized using different order Galerkin method into a series of ordinary differential equations.The modified 4th-order Runge-Kutta method is employed to solve the nonlinear transverse vibration equations by means of Matlab code.The numerical results also obtained by the Newmark-β method based on finite element analysis.The effects of parameters changing with the moving loads are also simulated.The results demonstrate the correctness of the proposed physical and mathematical models and the effectiveness of the solutiion methods with time varying parameters.It also indicates that the proper choosing of Galerkin truncation order can achieve better convergence and calculation accuracy in different situations.
vibration and wave;travelling string with time-varying length;Galerkin method;Newmark-β method;moving force;transversely forced vibration
TB123
ADOI编码:10.3969/j.issn.1006-1335.2016.03.004
1006-1355(2016)03-0016-05+56
2015-06-10
国家自然科学基金资助项目(51305115)
杨历(1989-),男,四川广元人,硕士生。
陈恩伟(1979-),男,广西合浦人,副研究员,硕士生导师。E-mail:cangxiyuanxi@163.com

