基于Stewart平台微振动主动控制分析与实验
李乔博,王超新,黄修长,张志谊
基于Stewart平台微振动主动控制分析与实验
李乔博,王超新,黄修长,张志谊
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
以压电棒为主动元件构建立方体Stewart隔振平台,采用基于DSP的数字控制系统和Fx-LMS自适应算法进行振动控制。对输入输出通道辨识方法和主动控制模块进行测试,并给出隔振平台隔振效果验证。实验结果表明,对于10 Hz~100 Hz范围内的单频干扰,可实现24 dB以上抑制效果,对于双频干扰,也具有良好的控制效果。
振动与波;微振动;主动控制;Stewart隔振平台;Fx-LMS自适应控制算法
航天器微振动干扰是影响航天器的指向精度和观测分辨率的重要因素[1]。由于航天器力学环境极为复杂和特殊,而且振动微小,使得分析与控制难度都很大。六自由度的Stewart平台被广泛的应用于精密系统的主动隔振中,具有明显优势和潜力。利用Stewart平台实现六自由度隔振主要有被动式、主动式和半主动的隔振方法[2]。被动式隔振系统具有内在的稳定性,对于高频响应,隔振效果较好,但被动隔振系统无法隔离航天器上低频扰动。主动振动控制由于作动器的存在,具有性能好、可靠性高、易于扩展以及易于实现多机分布并行处理等优势,在航空航天、工业控制、医疗设备、消费类电子、通信、计算机及科学研究的各个领域获得了越来越广泛的应用。以数字信号处理器作为核心部件,取代与数据采集卡相结合的PC机作为控制系统已成为可能[3]。
本文采用Stewart平台对有效载荷进行多自由度振动主动控制,以DSP为运算核心构建控制系统,采用Fx-LMS自适应算法进行主动控制,并进行实验测试。
1 Stewart隔振平台的结构
Stewart平台机构是一个由六自由度并行构成的六脚结构。其一般由上载荷平台,下基础平台和六个移动副及连接铰组成。有研究表明,不同构型的Stewart平台在应用于隔振场合时,性能效果差异很大,因此必须根据需求选择合适构型的Stewart平台进行主动控制[4]。为了简化运动学和动力学的复杂性,简化机构设计,方便控制解耦。本文选取一种立方体结构的Stewart平台,如图1所示。立方体的六条红色实线棱作为Stewart平台的支腿,ABC平面和EFD平面作为Stewart平台的载荷平面和基础平面。
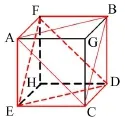
图1 立方体结构的Stewart平台示意图
相比较于一般结构的Stewart平台,立方体结构的Stewart平台具有任意两个相邻的主动杆支腿之间呈90°关系,具有正交性,能实现在三个相互垂直轴线方向上的运动解耦,并且各方向的控制能力和刚度具有一致性的优点。
基于上述立方体结构,采用压电棒作为主动元件,设计出Stewart隔振平台如图2所示。
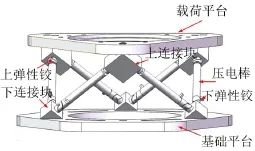
图2 Stewart隔振平台模型
2 Stewart隔振平台的主动控制原理
主动控制方法是基于LMS算法的Fx-LMS自适应算法,该算法弥补了系统的传递函数给LMS算法带来的影响。
最小均方(LMS)算法通过采用误差信号单个样本方差的负梯度代替均方误差的负梯度来调节滤波器的权系数使二次性能指标(误差信号均方值或平均功率)达到最小。自适应前馈主动减振的原理可由图3所示的系统辨识的框图来说明:当自适应过程收敛时,w(z)是p(z)的最佳估计,y(n)能最好地再现d(n),此时误差信号e(n)最小。如果d(n)是需要控制的振动,y(n)与d(n)的反向叠加则会使残余振动或噪声信号e(n)最小,这便达到了振动或噪声控制的目的。
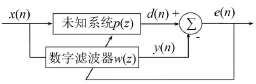
图3 自适应系统辨识框图
在实际应用中,误差信号e(n)并不是滤波器输出y(n)与期望信号d(n)的简单叠加。在y(n)与e(n)之间存在一个次级通道的传递函数s(z),s(z)为误差通道的脉冲响应函数s(n)的z变换,如图4所示。

图4 主动控制系统简化框图
在物理上误差通道s(z)包括D/A、功率放大器、主动执行机构、被控系统、误差传感器和A/D等环节,公式如下
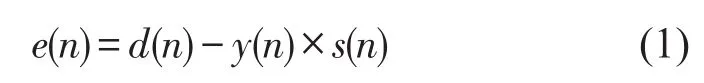
由于误差通道的存在,标准的LMS算法中对性能函数负梯度的估计会产生偏差,从而使权向量的调整不是严格地沿最陡下降的方向调整。这将对自适应进程产生不良影响。
为了消除误差通道的影响,Morgan提出两种解决方案[5]。一种是将s(z)满足某种条件下辨识出的逆滤波器级联在误差通道的前面,以消除它的影响。Scott Sommerfeldt和Jiry Ticky将这种方法应用于双层隔振系统的主动控制研究[6]。杨铁军等在他们的研究中也采用了这种办法,取得了满意的控制效果[7]。相应的算法称为MLMS算法。第二种办法是将s(z)的数字模型ŝ(z)放在参考信号参与调节滤波器权系数之前,如图5所示。Fx-LMS算法分别由Widrow在自适应控制领域和Burgess在噪声主动控制领域的应用中推导得出。
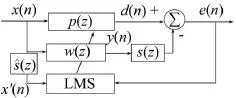
图5 运用Fx-LMS算法的主动控制系统框图
定义控制器的参考输入向量为
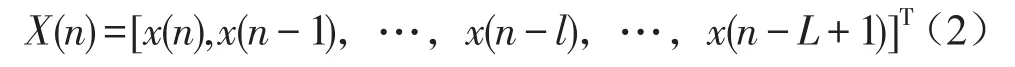
滤波器权值向量
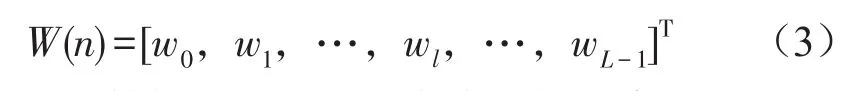
其中n表示采样时刻,L表示滤波器的长度。则控制器的输出可以写成
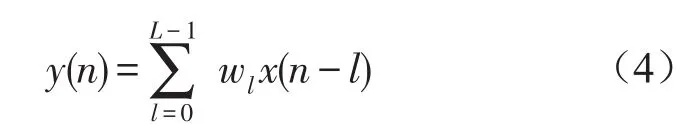
误差通道用长度为H的FIR滤波器表示,其权向量为
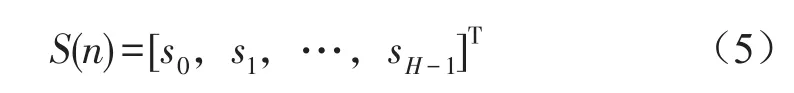
图5中w(z)和s(z)分别表示滤波器权向量W(n)和误差通道滤波器S(n)的z变换,即
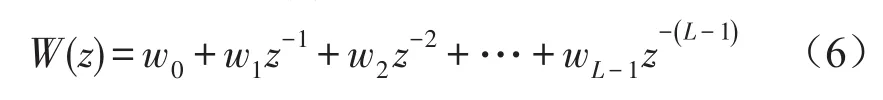
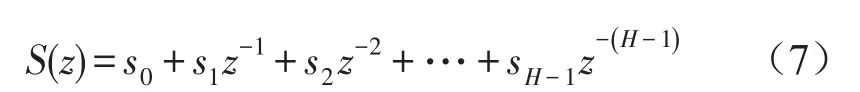
则误差传感器的输出可写成
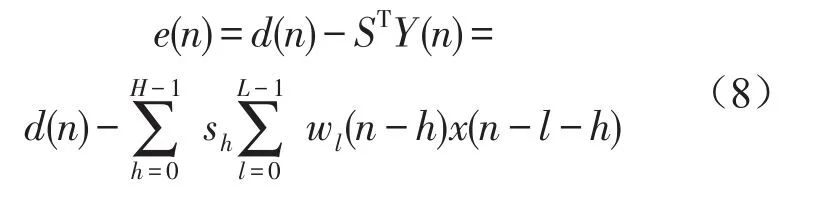
变换求和顺序,则
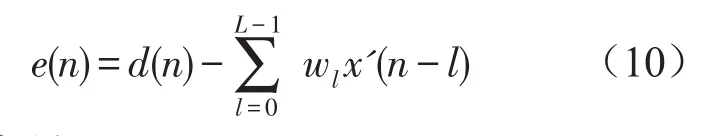
定义如下向量
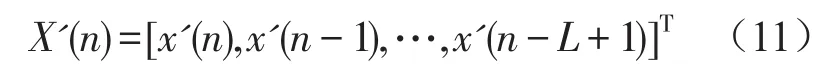
误差信号可写成如下形式
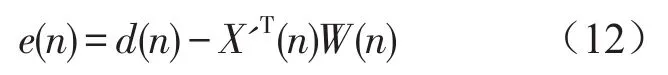
取性能函数为

将式(12)代入上式(13),则性能函数可以写成
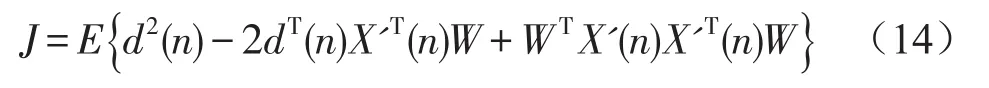
按标准的LMS算法的推导过程,可以得到类似的结果,即最佳权向量表达式为

权向量更新公式
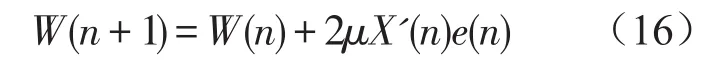
而整个滤波Fx-LMS算法可简单地归纳如下
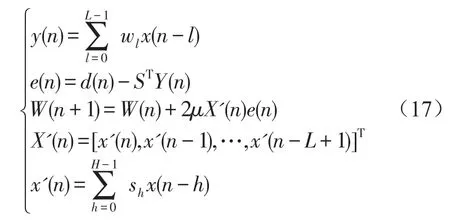
3 Stewart隔振平台的主动控制系统
随着用户对微处理器的多核协作、更高集成度外设、更低热量耗散以及更低总体系统成本的需求,TI公司推出了新一代的低功耗OMAP-L138双核处理器[8]。考虑到经济成本和售后支持服务,本文选用DEC 138控制板作为控制系统的处理器,控制板拥有6路A/D和4路D/A。
Stewart隔振平台的主动控制过程主要包括两个部分:次级通道辨识过程和主动控制过程。估计次级通道传递函数的过程称为次级通道的建模过程。在实际应用中,先关闭外部干扰源,采用DSP产生的高斯白噪声作为次级通道建模的激励源,辨识一定次数后,转而进入主动控制过程。这样,整个控制过程的流程如图6所示。
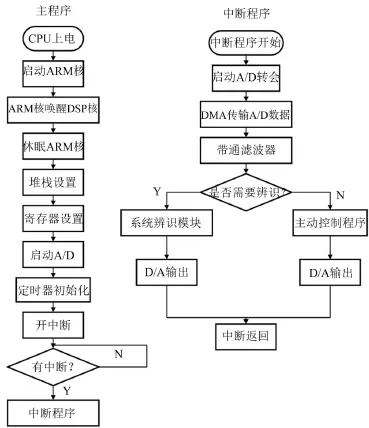
图6 主动控制流程图
如图所示,为了精确地控制采样率,使用DSP内部的定时器控制采样时间间隔T,设置定时器的定时时间等于采样时间间隔T,并让它工作在中断方式,则定时器每过T时间就向CPU发出中断请求,CPU响应中断请求,转去执行中断服务程序,在中断服务程序中读取A/D转换结果,对转换结果进行运算,通过带通滤波器后将运算结果送D/A转换器转换为模拟量,在经过带通滤波器后输出。因此,程序分为A/D转换、定时器中断、中断服务程序、带通滤波、D/A转换等几个模块。
3.1控制系统A/D和D/A功能测试
使用WD 990微机电源为控制板供电,采用FG-506信号发生器作为信号源对A/D功能进行测试,如图7所示。
利用定时器加中断的方式确定采用频率里使用1 kHz的采样频率对100 Hz±3 V的正弦信号进行采样,取200个采样点,在CCS上可以观测到该正弦曲线,采样效果良好。
同样地,由WD 990微机电源为D/A模块提供± 15 V的工作电压和±10 V的参考电压,编写程序输出频率为1 kHz,幅值为±4 V的正弦输出信号,在示波器上可以观测到该正弦信号。由此可见,控制系统的A/D和D/A功能良好。

图7 控制器A/D功能测试
3.2次级通道建模算法的仿真
为了对系统辨识算法进行仿真,假设要辨识的通道模型为P(z)=(0.002 5,0.062 5,0.125,0.25,0.125,0.062,5)[9],取参考信号x(n)为高斯白噪声,W(z)的阶数取150阶,步长mu=0.1,辨识次数为10 000次,利用开发板仿真得到的结果如图8所示。取前16阶观察,可以看到,利用自适应的算法可以很好地辨识出系统的脉冲响应函数。
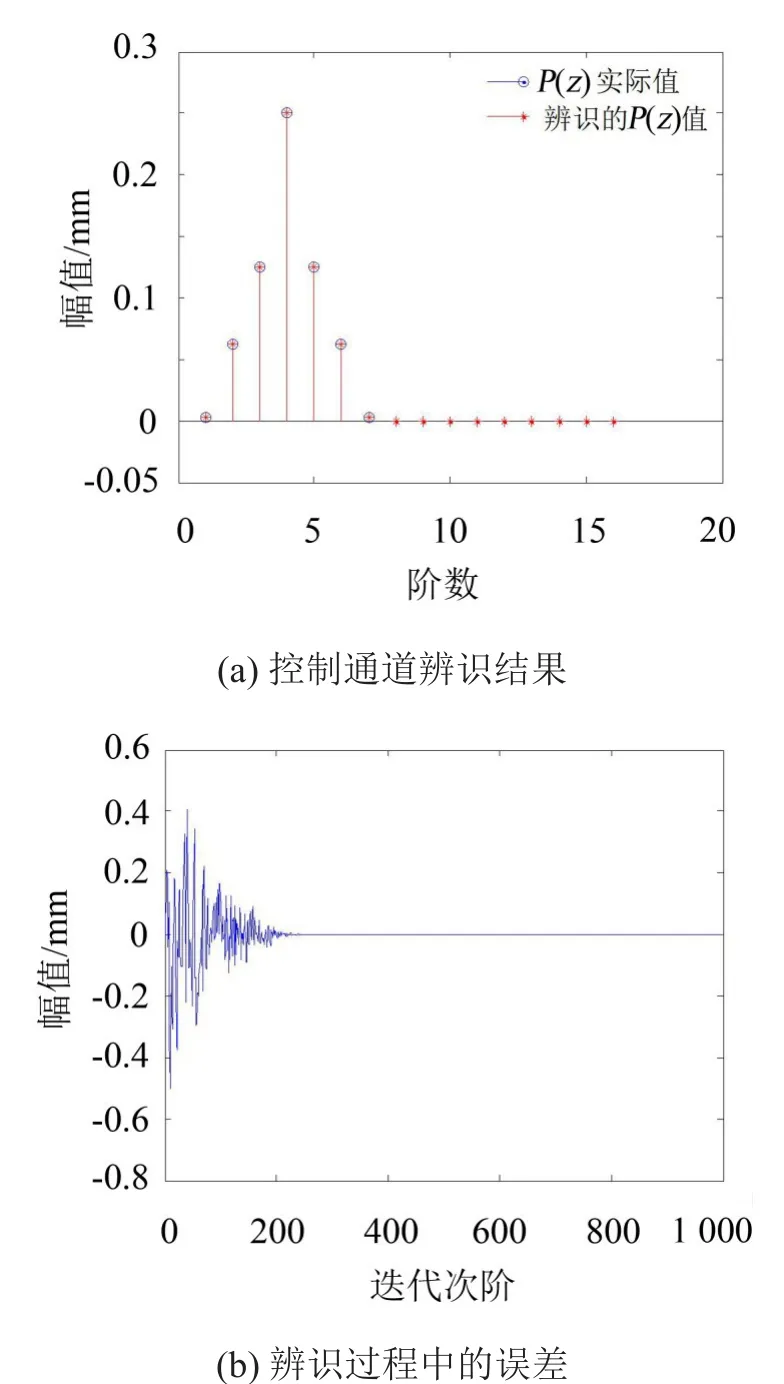
图8 利用控制板对系统辨识的测试
3.3主动控制算法的仿真
利用控制板对主动控制模块进行了仿真,这里给出的干扰信号是20 Hz和40 Hz幅值为1 mm的正弦方波叠加的干扰信号,权值Wz取32阶,步长mu 取0.01,控制通道取上述辨识算法测试中的P(z),结果如图9所示,经计算,无控制时,信号RMS值为0.995 mm,有控制时为1.303×10-3mm。
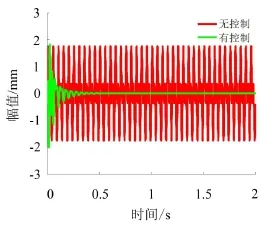
图9 利用控制板进行的主动控制仿真
4 Stewart隔振平台主动控制实验
Stewart隔振平台主动控制实验布置如图10所示,数据采集仪器(LMS)主要用于采集平台各方向的振动信号,同时也用于微振动干扰源的信号频率和幅值的控制。加速度计信号先通过电荷放大器调理,然后分别由数据采集仪器和DSP接受,DSP对控制目标信号进行处理,并通过D/A通道发出控制信号,经过滤波器和功率放大器,推动隔振平台6个压电棒产生运动。为了更好地隔离来自地面的振动,将整个隔振平台布置到一个装满细沙的长方体玻璃容器中,同时在容器下端放置了橡胶减振器。
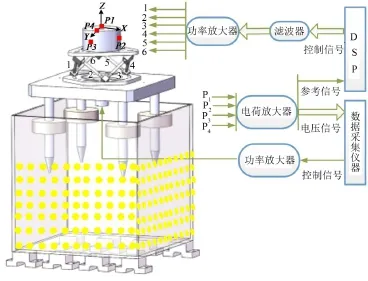
图10 Stewart隔振平台实验布置图
根据立方体Stewart隔振平台的雅克比矩阵可知[10],杆的伸长量d和上平台6个方向的运动关系的如式(18)所示,压电棒的最大伸长位移s=±40 μm,由公式求解6个方向的纯位移可以得到表1伸长量。
因此,4路D/A信号完全可以控制Z轴和绕X轴转向的振动。对于Stewart隔振平台的主动控制,重点描述对于Z方向的控制效果。如果采用单频激励,Stewart隔振平台的控制效果如表2所示衰减量。


表1 平台6个方向为纯运动时6杆伸长量
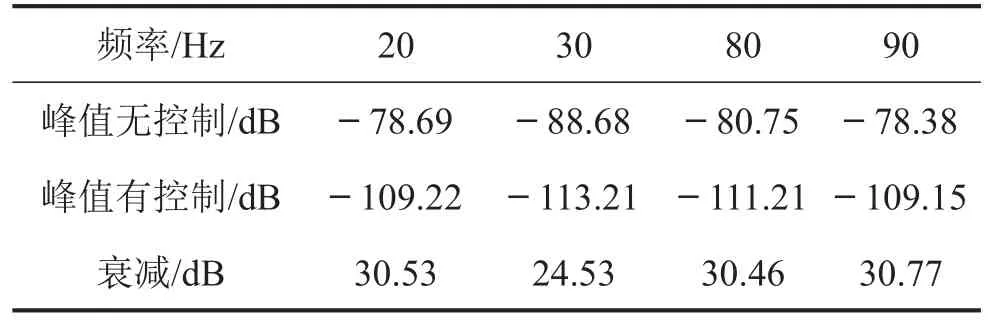
表2 不同频率激励下振动衰减
为了验证隔振平台对双频干扰的抑制效果,选取代表性的双频30 Hz和70 Hz激励下控制端有、无控制对比结果说明主动控制对双频干扰的有效性,如图11所示。
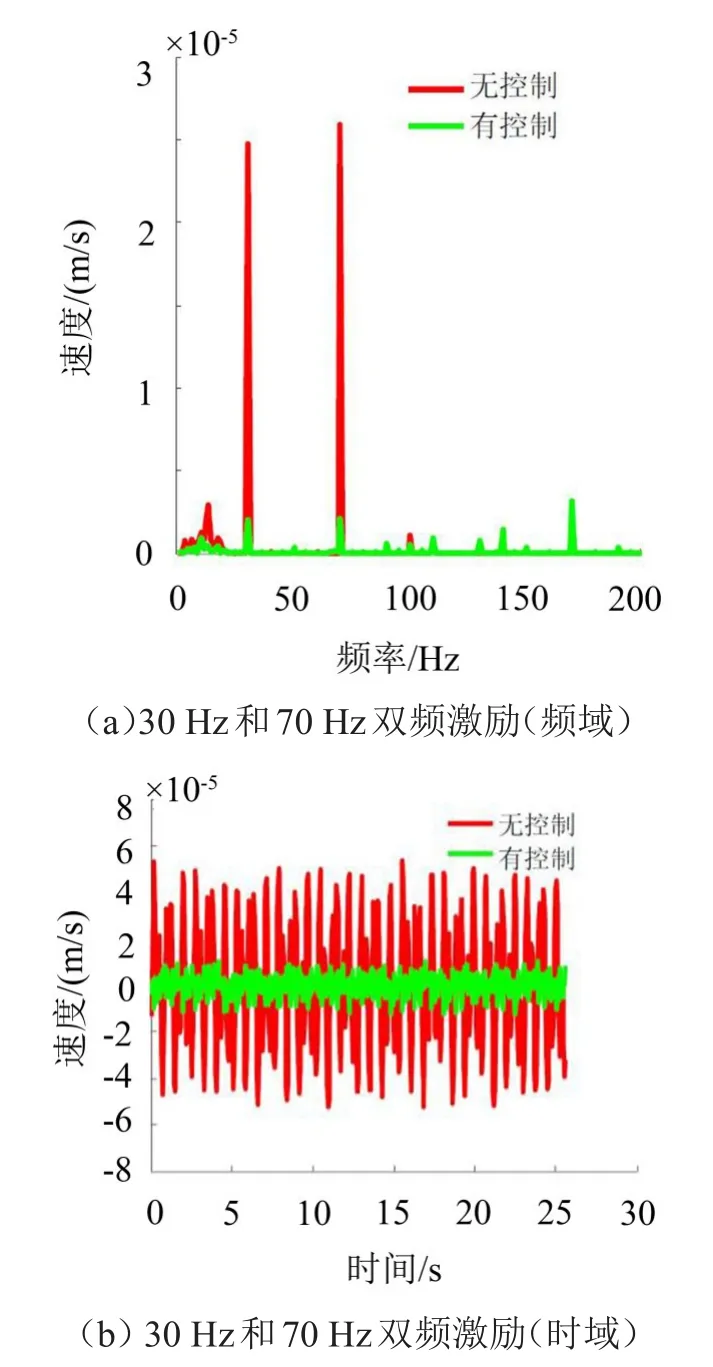
图11 Stewart主动隔振平台实验结果
从图11可以明显看出,抑制效果明显。控制后,在30 Hz对应的主峰衰减为21.83 dB,70 Hz对应的主峰衰减为21.7 dB。
5 结语
本文针对一个采用压电陶瓷材料作为主动控制元件的立方体Stewart隔振平台,设计了基于DSP的控制系统,采用自适应控制算法,实现了隔振平台垂直方向的振动控制,对于单频干扰取得了24 dB以上的衰减效果,对于双频干扰也具有良好的控制效果。
[1]马俊.用于微振动控制的隔振器分析和实验[J].噪声与振动控制,2015,35(2):205-208.
[2]THAYER D,CAMPBELL M,VAGNERS J,et al.Six-axis vibrationisolation system using soft actuators and multiple sensors[J].Journal of Spacecraft and Rockets,2002,39(2):206-212.
[3]王慰慈,周炎,饶柱石.轴系振动监测系统的开发与试验验证[J].噪声与振动控制,2012,32(1):145-148.
[4]GENG Z J,HAYNES L S.Six degree-of-freedom active vibration control using the Stewart platforms[J].IEEE Transactions on Control Systems Technology,1994,2(1):45-53.
[5]MORGAN D R,SANFORD C.A control theory approach to the stability and transient analysis of the filtered-x LMS adaptive notch filter[J].IEEE Transactions on Signal Processing,1992,40(9):2341-2346.
[6]SOMMERFELDT S D,TICHY J.Adaptive control of a two:tage vibration isolation mount[J].Journal of the Acoustical Society ofAmerica,1990,88(2):938-944.
[7]杨铁军,靳国永,李玩幽,等.舰船动力装置振动主动控制技术研究[J].舰船科学技术,2006,28(增刊2):46-53.
[8]雷伊.OMAP-L138 DSP原理与应用实例[M].北京:科学出版社,2014.
[9]LAN H,ZHANG M,SER W.A weight-constrained Fx-LMS algorithm for feedforward active noise control systems[J].IEEE Signal Processing Letters,2002,9(1):1-4.
[10]孔宪仁,刘磊,王萍萍.Stewart平台动力学建模及鲁棒主动隔振控制[J].宇航学报,2011,32(6):1231-1238.
Analysis and Experiment of Micro-vibrationActive Control Based on a Stewart Platform
LI Qiao-bo,WANG Chao-xin,HUANG Xiu-chang,ZHANG Zhi-yi
(State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University,Shanghai 200240,China)
With the piezoelectric stack as an active element,a cubic Stewart platform is constructed.The digital control system based on DSP and Fx-LMS algorithms is adopted to suppress the foundation vibration.The input and output channel identification system and the active control module are tested.And the vibration isolation effect of the Stewart platform is verified.The results show that for the tonal disturbance ranged from 10 Hz to 100 Hz,the Stewart platform can achieve 24 dB attenuation effect.The platform also performs well under a mixed disturbance condition.
vibration and wave;micro-vibration;active control;Stewart platform;Fx-LMS algorithms
O328,O329
ADOI编码:10.3969/j.issn.1006-1335.2016.03.044
1006-1355(2016)03-0214-05
2015-01-18
上海市教育委员会和上海市教育发展基金会晨光计划资助项目(13CG08)
李乔博(1990-),男,江苏省沛县人,硕士生,主要研究方向为振动控制。E-mail:joebrandy@126.com
张志谊,男,博士生导师。E-mail:chychang@sjtu.edu.cn

