弹性支撑旋转Timoshenko梁动力学特性
黄意新,赵 阳,田 浩,李慧通
弹性支撑旋转Timoshenko梁动力学特性
黄意新,赵阳,田浩,李慧通
(哈尔滨工业大学 航天学院,哈尔滨 150001)
为研究弹性支撑旋转梁动力学特性随转速及弹性支撑参数变化规律,考虑剪切效应、转动惯量和陀螺效应,采用Hamilton原理推导旋转Timoshenko梁动力学方程,应用Chebyshev谱方法获得系统涡动频率与模态振型数值解。结果表明,在高速转动状态下陀螺效应、支撑结构刚度对Timoshenko梁动力学特性有显著影响;各阶固有频率随着转速增加而分成正向涡动频率与反向涡动频率,高阶频率变化幅度更大;涡动频率随支撑结构直线刚度增加而呈阶梯状变化,当直线刚度增加到一定值后系统涡动频率将保持稳定;随着支撑结构转动刚度增加,涡动频率出现一个最小值与最大值,前者低于自由边界条件下频率值,后者高于固定边界条件下频率值。相关结果可用于各类旋转梁机构的设计与优化。
振动与波;旋转Timoshenko梁;弹性支撑;Chebyshev谱方法;陀螺效应;涡动频率
旋转梁结构广泛应用于各类工程机械中,包括燃气轮机、卫星、发动机及各类机床设备等,其动力学特性对机械效率与加工精度至关重要[1-2]。随着高速切削等加工技术的发展,各类旋转梁结构转速逐渐升高,可达180 000 r/min[3]。由于旋转运动产生的离心力及科氏力效应,旋转梁的固有频率、模态振型及动力学响应均与非旋转梁不同[4]。随着转速增加,梁的振动幅度可能增大,影响设备稳定性与精度,甚至造成损坏。因此,在精密旋转机械设计与制造中,需要对旋转梁的涡动频率、模态振型、临界转速等动力学特性进行准确分析。
对于高速旋转的非细长梁,需要考虑其剪切效应与转动惯量效应,因此需要采用Timoshenko梁理论[5]。目前对旋转Timoshenko梁动力学特性的研究多集中于自由、固支、铰支等一般边界条件,工程中轴系设计多半是根据刚性安装状态进行设计[6],而实际工程中支撑结构并非完全刚性支撑,弹性支撑边界条件对系统动力学特性有显著影响[7-8],因此有必要对弹性支撑旋转梁的动力学特性作系统分析。由于旋转运动引起的附加效应,如陀螺效应,使得旋转梁的分析变得更为复杂,增加了控制方程的数值求解难度[9]。谱方法是继差分法和有限元法之后又一种重要的数值方法,它用在整个区间都非零的连续函数的线性组合来逼近精确解,其精度可直接由级数展开式的项数来决定,具有指数收敛特性,常被视为具有“无穷阶”收敛性,当真解足够光滑时,采用谱方法可以得到很好的效果。谱方法可应用于微分方程数值求解[10],梁动力学问题分析等[11]。从函数近似的角度看,谱方法可以分为Fourier方法,Chebyshev或Legendre方法。前者适用于周期性问题,后者适用于非周期性问题。
本文采用Timoshenko梁理论和Hamilton原理推导弹性支撑旋转Timoshenko梁动力学方程,采用Chebyshev谱方法数值求解旋转梁涡动频率、模态振型,研究分析了转速、弹性支撑刚度等参数对旋转梁动力学特性的影响。
1 动力学模型
图1为一等截面旋转梁,长度为L,密度为ρ,圆截面半径为r,面积为A,以恒定角速度Ω旋转,XYZ为固定直角坐标系,Z轴与变形前的梁中线重合。转动坐标系xyz随梁以角速度Ω旋转,z轴与Z轴重合。坐标系ξηζ为局部正交坐标系,原点位于截面微元中心。梁两端与支撑结构的连接采用直线弹簧和转动弹簧表示,kx0、kxL分别为梁两端连接处x方向的直线刚度,ky0、kyL为梁两端连接处y方向的直线刚度,kαx0、kαxL为xoz平面内转动刚度,kαy0、kαyL为yoz平面内转动刚度,在图中没有绘出。
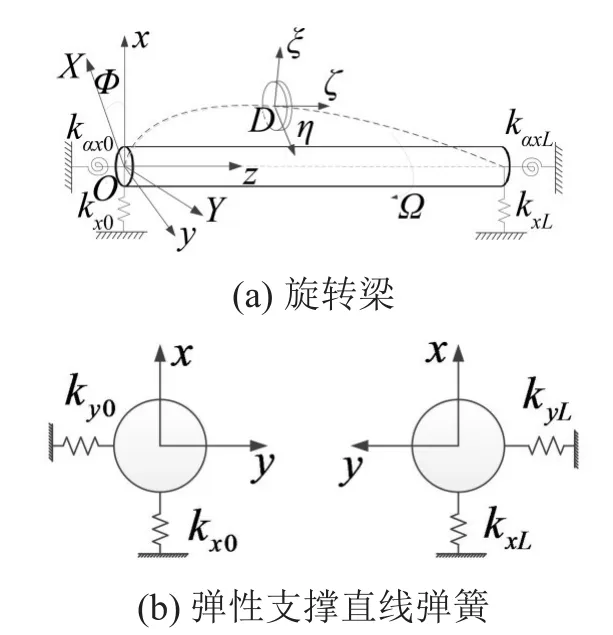
图1 弹性支撑旋转梁模型
采用Timoshenko梁模型,变形后微元质心矢径在坐标系xyz中可表示为
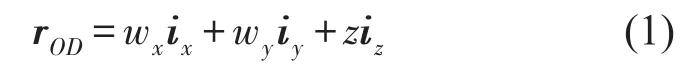
式中ix、iy、iz是坐标系xyz的基向量,wx、wy为微元中心沿x、y方向的弹性变形。则质心平动速度为
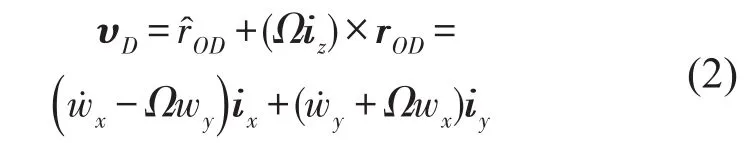
系统平动动能为
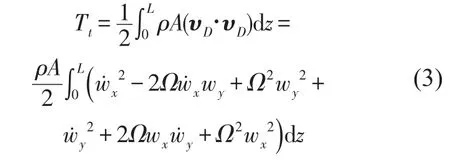
Timoshenko梁微元段变形如图2所示,剪切角β与弯曲变形角α关系为
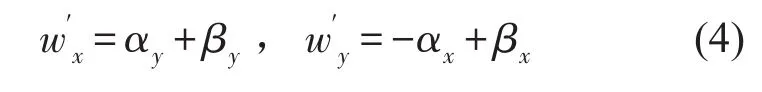
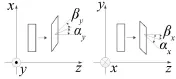
图2 梁微元弯曲与剪切变形
由于梁的弯曲,微元分别绕x、y轴转动角度αx、αy,则微元角速度可表示为
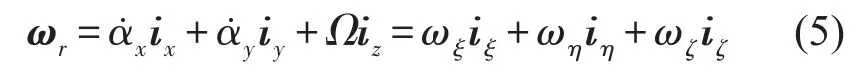
式中ωξ、ωη、ωζ分别为微元绕ξ、η、ζ轴转动的角速度。由欧拉运动学方程可得
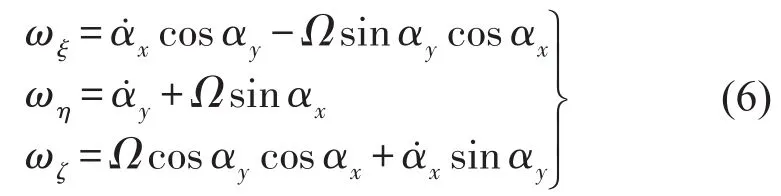
基于小变形假设,式(6)可简化为
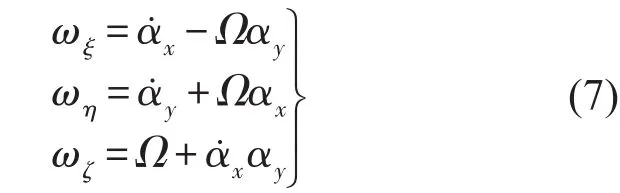
则系统转动动能为
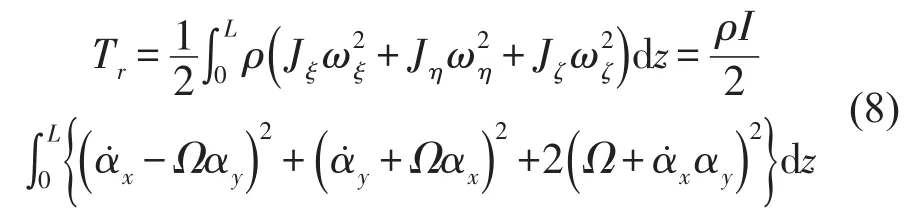
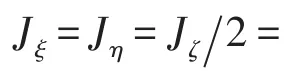
系统动能由平动动能和转动动能两部分组成

旋转梁变形势能由弯曲变形能与剪切变形能组成,考虑式(4),变形能可表示为
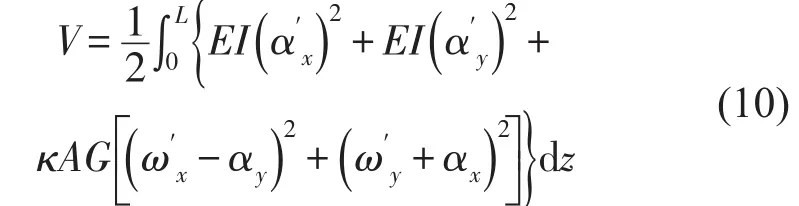
式中E为杨氏模量,G为剪切模量,κ为剪切系数。
fx、fy、Mx、My为作用在梁上的分布作用力和力矩,则非保守力所作虚功为
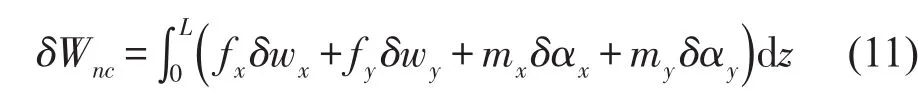
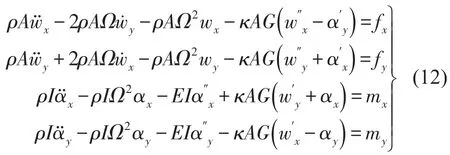
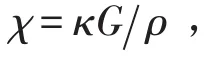
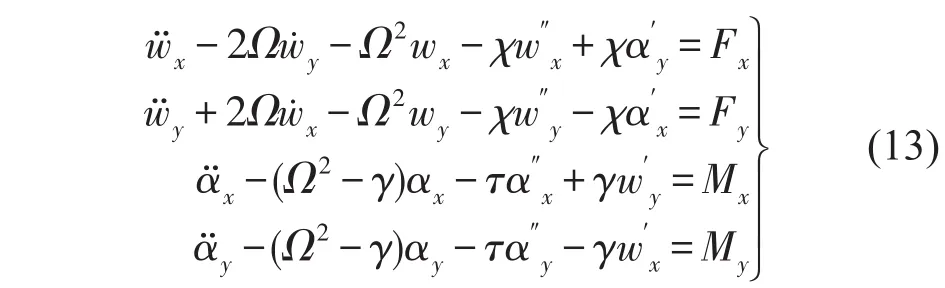
弹性支撑边界条件可表示为在z=0,L时有
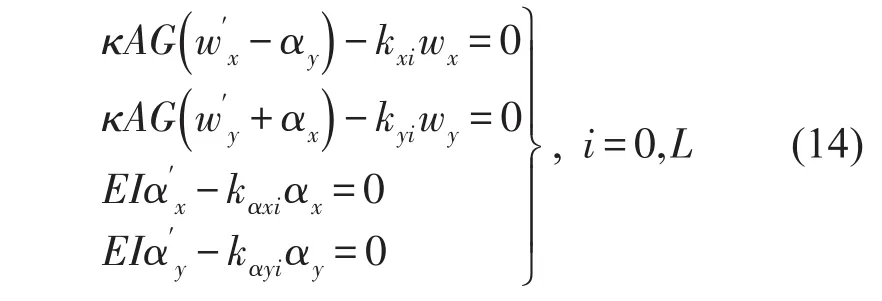
2 动力学方程分析
2.1Chebyshev谱方法
根据谱方法中级数展开方法的不同,谱方法分为Fourier方法和Chebyshev方法等,本文中采用Chebyshev多项式作为级数展开时的基函数,即Chebyshev谱方法。Chebyshev多项式有两类,本文采用第一类Chebyshev多项式,它是一类递归正交多项式,其第k项可表示为
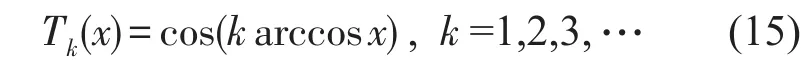
且满足递推关系
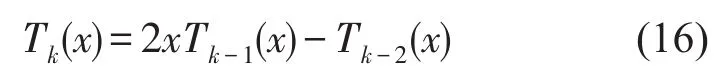
式中x∈[-1,1]。函数y(x)的N-1阶Chebyshev多项式逼近为
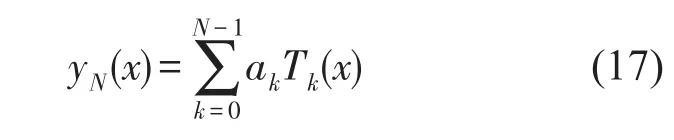

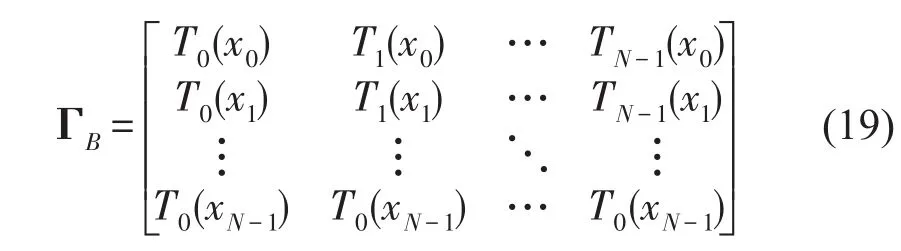
Chebyshev多项式导数
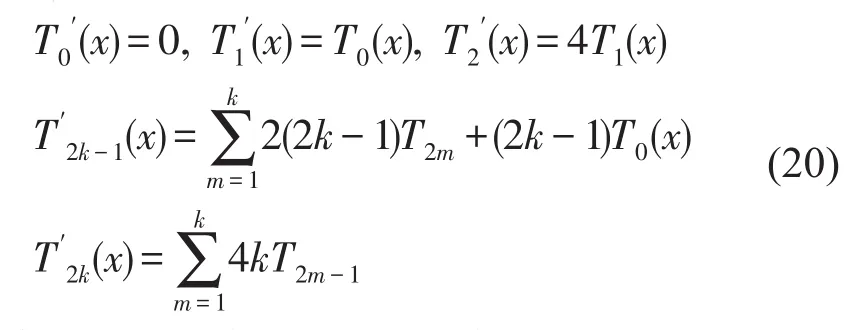
式中k>1,由式(17)、(20)可得
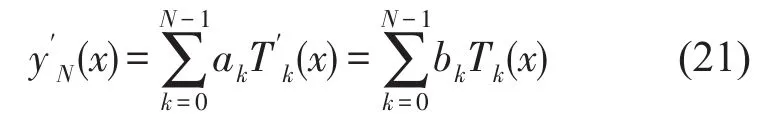
多项式系数bk组成N维向量b

式中变换矩阵D可由式(20)、(21)获得。综合式(21)、(22)可得函数y(x)的n阶导数值
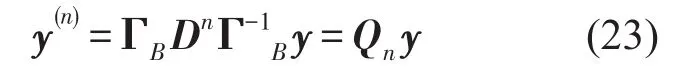
Qn为n阶Chebyshev微分矩阵。根据式(23),可由函数y(x)采样点值求得其在采样点处的各阶空间导数值。
2.2离散动力学方程
由式(13)及式(23)可得旋转Timoshenko梁动力学方程的离散形式为
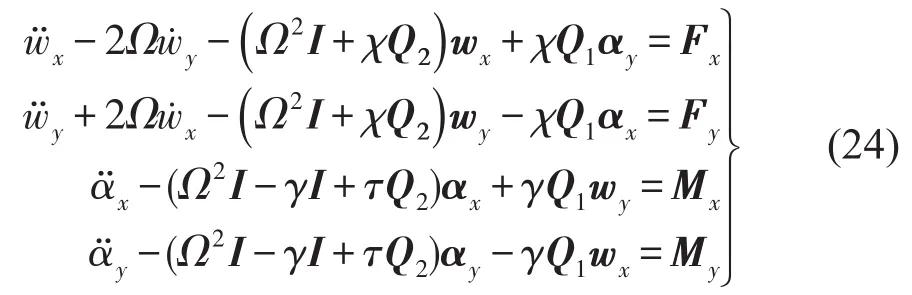
式中wx、wy、αx、αy均为N维列向量,其元素分别为wx、wy、αx、αy在N个采样点上的值,I为N阶单位矩阵。
定义
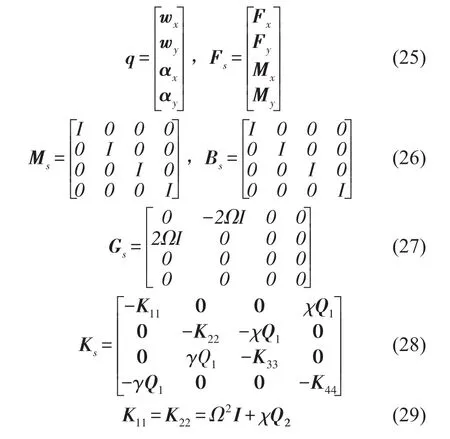
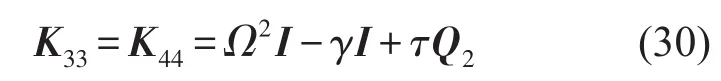
则旋转Timoshenko梁离散力学方程可表示为
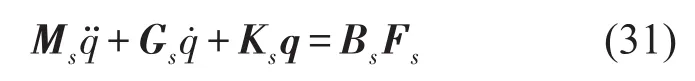
2.3弹性支撑边界条件
弹性支撑边界条件(14)的离散形式可表示为BEq=0,即
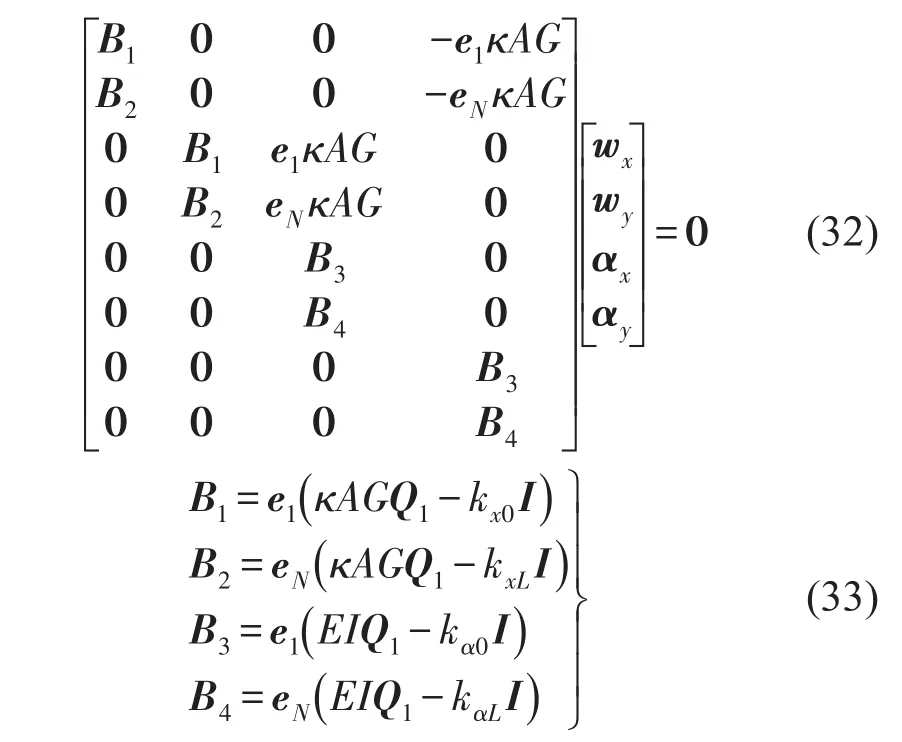
对于任意满足式(32)的解q可表示为

3 算例
数值计算采用如下参数:L=1.3 m,r=0.05m,κ=0.88,ρ=7 800 kg/m3,E=2.0×1011N/m2,G= 7.7×1010N/m2。图3(a)为Ω=10 000 r/min,kx0= kxL=2×109N/m,kα0=kαL=2×109N∙m/rad时旋转梁前3阶反向涡动与正向涡动模态振型(正向涡动方向与梁旋转方向一致,反向涡动频率则与之相反),二者基本一致,有微小的不同。图3(b)为弹簧刚度变为 kx0=kxL=5×109N/m,kα0=kαL=5×109N∙m/rad时的涡动模态振型,二者对比可以看出相较于刚性支撑两端固支时,其两端位移均不再为零,且随着支撑刚度的降低而增大。
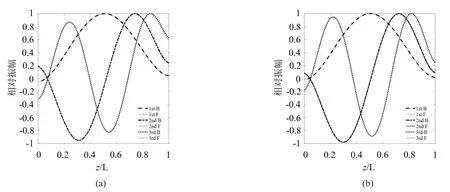
图3 前3阶涡动模态振型
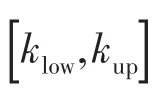
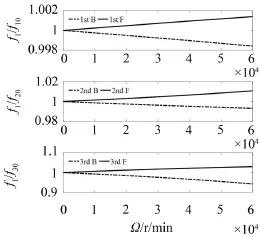
图4 涡动频率随转速变化规律
图6为旋转Timoshenko梁前3阶固有频率随转动刚度kα0、kαL的变化规律,Ω=10 000 r/min时,从图中可以看出,各阶正、反涡动频率随转动刚度变化存在两个极值,在二者之间各阶频率随转动刚度增大而增大,当达到最大值后逐渐降低收敛于刚性支撑下的相应频率值。为保证弹性支撑旋转梁动力学特性稳定,转动刚度应大于频率最大值对应的转动刚度kup,此外还可以利用此特性需获得比刚性支撑条件下更高的固有频率特性或比自由边界条件下更低的固有频率。
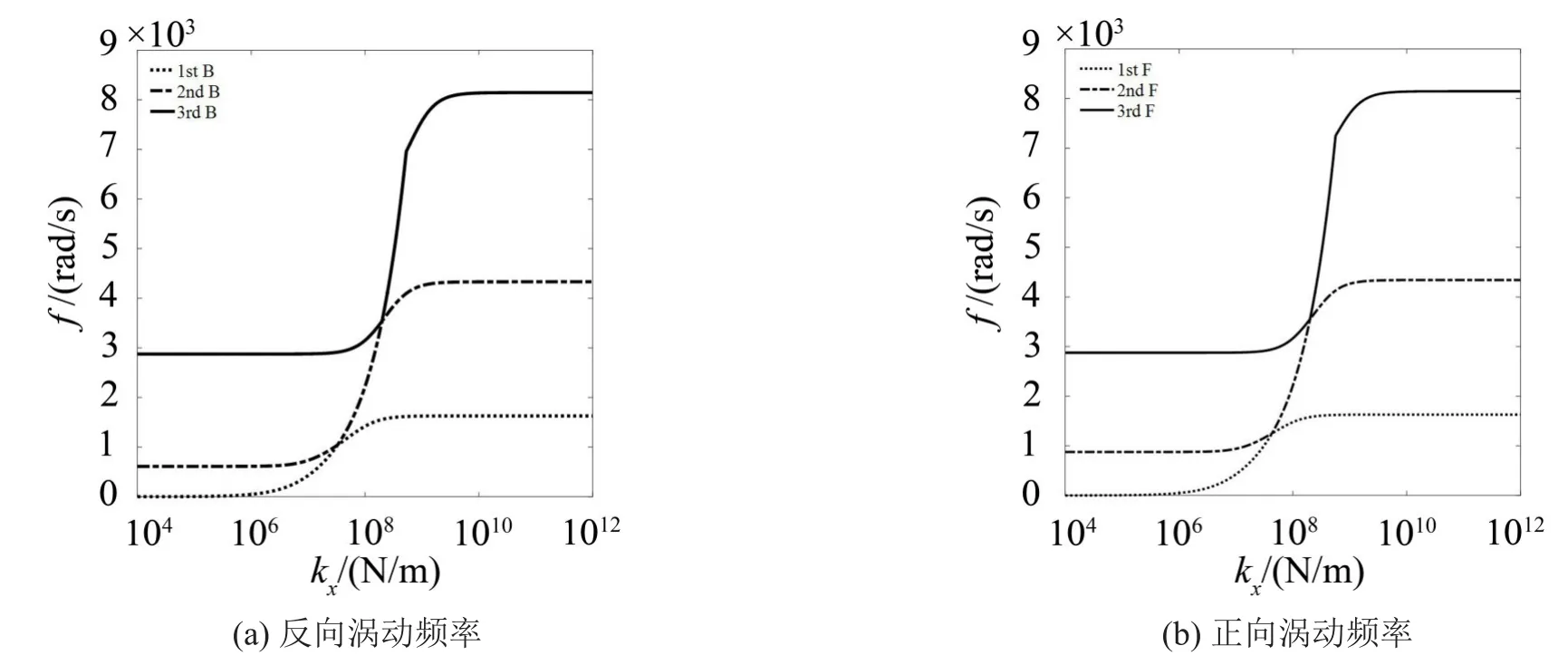
图5 Ω=10 000 r/min时直线刚度对涡动频率的影响
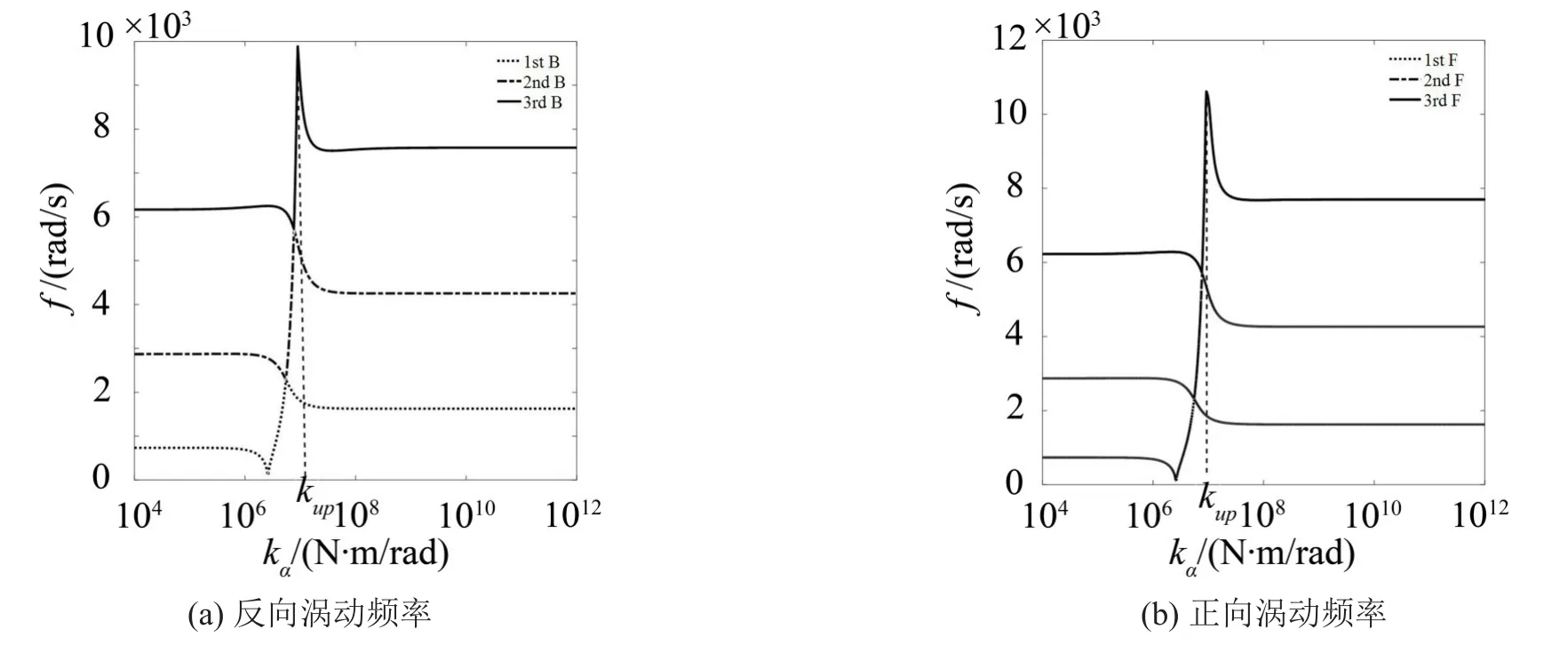
图6 Ω=10 000 r/min时转动刚度对涡动频率的影响
4 结语
本文推导了旋转Timoshenko梁的动力学方程,通过Chebyshev谱方法获得了弹性支撑边界条件下各阶涡动频率与模态振型,得出以下结论。
(1)弹性支撑条件下旋转梁涡动频率与模态振型与刚性支撑不同,各阶模态振型边界处振幅不为零,且随支撑刚度的降低而增大。
(2)旋转梁固有频率随着转速的增大而分成正向涡动频率、反向涡动频率两部分,正向涡动频率随着转速的增大而增大,反向涡动频率随着转速的增大而减小,其相对于非旋转梁固有频率的比值随着频率的阶次增大而增大。
(3)存在一直线刚度值区间,低于此区间时,旋转梁各阶频率几乎不变,高于此区间时各阶频率亦几乎不变,在此区间内,各阶频率随着刚度的增大而增大,为保证系统动力学特性稳定,应保证支撑直线刚度高于此区间并保有一定余量。
(4)存在一转动刚度区间,在此区间内各阶固有频率达到最大值和最小值,低于或高于此区间值,各阶频率随转动刚度的变化而变化很小,为保证系统动力学特性稳定,应保证支撑结构转动刚度高于此区间,此外可利用此特性获得比刚性支撑更高的固有频率或比自由边界条件下更低的固有频率。
[1]钱新,杜星文.旋转Rayleigh梁动力学性能的研究[J].力学学报,2011,43(3):635-640.
[2]PAI P F,QIAN X,DU X.Modeling and dynamic characteristicsofspinningRayleighbeams[J]. International Journal of Mechanical Sciences,2013,68(3):291-303.
[3]汪博,孙伟,闻邦椿.高转速对电主轴系统动力学特性的影响分析[J].工程力学,2015,32(6):231-256.
[4]NA S,YOON H,LIBRESCU L,et al.Effect of taper ratio on vibration and stability of a composite thin-walled spinning shaft[J].Thin-Walled Structures,2006,44(3):362-371.
[5]HAN S M,BENAROYA H,WEI T.Dynamics of transverselyvibrationbeamsusingfourengineering theories[J].Journal of Sound&Vibration,1999,225(5):935-988.
[6]钱大帅,王强勇,鲁民月,等.隔振对机械转子—轴承系统动特性的影响[J].噪声与振动控制,2014,34(4):88-91.
[7]刘开来.弹性边界下梁板结构动态特性分析[D].哈尔滨:哈尔滨工程大学,2013.
[8]周海军.推进轴系回旋振动及其支撑结构振动特性研究[D].哈尔滨:哈尔滨工业大学,2013.
[9]钱新.柔性旋转梁动力学特性理论与实验研究[D].哈尔滨:哈尔滨工业大学,2011.
[10]李雪慧.截断多项式的谱方法求解数值微分问题[D].兰州:兰州大学,2009.
[11]BARIS YAGCI,SINAN FILIZ,LOUIS L,et al.A spectral-Techbycher technique for solving linear and nonlinear beam equations[J].Journal of Sound and Vibration,2009(321):375-404.
[12]FILIZ S,ROMERO L A,OZDOGANLAR O B.An analytical model for micro endmill dynamics[J].Journal of Vibration&Control,2008,14(8):1125-1150.
Dynamic Characteristics of a Spinning Timoshenko Beam with Elastic Supports
HUANG Yi-xin,ZHAOYang,TIANHao,LI Hui-tong
(School ofAstronautics,Harbin Institute of Technology,Harbin 150001,China)
The dynamic characteristics of a spinning Timoshenko beam with elastic supports are investigated.The model of the beam is built and the rotatory inertia,shear effects and gyroscopic effects are considered.The governing equation is derived based on the extended Hamilton's principle and is numerically solved by Chebyshev spectral method,and the natural frequencies and modals are obtained.It is shown that the gyroscopic effects and the support stiffness have a significant effect on the dynamic characteristics of the spinning Timoshenko beam.The natural frequencies are split into forward whirl speed and backward whirl speed,the distinction between the forward and backward whirl speeds becomes more obvious for higher order modes.The whirling speeds vary in step-wise with translational spring stiffness increasing and become stable when the stiffness exceeds a critical value.Two extremum values appear as the rotational stiffness increasing,the minimal value is smaller than the corresponding value under the free boundary condition and the maximum value is bigger than the corresponding value under the fixed boundary condition.The results can be used for designing and optimizing the mechanism of rotating beams.
vibration and wave;spinning Timoshenko beam;elastic supports;Chebyshev spectral method;gyroscopic effects;whirling speeds
O326
ADOI编码:10.3969/j.issn.1006-1335.2016.03.002
1006-1355(2016)03-0006-05+15
2015-12-25
国家重点基础研究发展973计划资助项目(2013CB733004)
黄意新(1987-),男,湖南衡阳人,博士生,主要研究方向为航天器结构动力学。E-mail:huangyixin87@126.com

