圆柱绕流噪声预报的流场与声场模拟方法对比研究

张翰钦，陈　明，孙国仓

圆柱绕流噪声预报的流场与声场模拟方法对比研究

张翰钦，陈明，孙国仓

（武汉第二船舶设计研究所，武汉 430205）

以三维圆柱为研究对象，使用Lighthill声类比法研究其绕流发声问题。第一步进行流场计算，分别用大涡模拟（LES）、脱体涡模拟（DES）和瞬态雷诺平均法（URANS）模拟声源区流场，通过对比流场压力和涡量等参数，据此选取合适的流场仿真方法；第二步用基于Lighthill方程FW-H积分法和边界元法预报远场直发声，通过和Revell试验结果比较，分析各种计算方法差别。研究表明：进行流场仿真时LES计算结果最好，IDDES法在保证计算精度条件下能有效减少流场网格数量，URANS法误差很大；进行辐射噪声预报时，FW-H积分法和边界元法基本相同。

声学；流噪声；大涡模拟；脱体涡模拟；Lighthill声类比

圆柱结构作为一种基本的结构形式，在交通运载工程、海洋工程和流体机械等领域都很常见，流体介质在流经圆柱结构后，在一定雷诺数下，圆柱尾流会交替出现脱落涡，这些涡街引起圆柱表面的脉动压力，从而产生噪声。圆柱绕流发声问题很早就有学者作了研究。1977年，Revell通过风洞试验，以直径19 mm和38 mm的圆柱为研究对象，测试马赫数从0.1到0.5之间，雷诺数从45 000到450 000间变化，Revell测量了该雷诺数范围圆柱绕流的阻力系数及总声压级等数据，研究了圆柱绕流阻力和流噪声之间的关系［1］。该实验已作为一个基准算例，提供给众多的研究者作为计算参考。数值仿真方面，针对该问题，Kenneth S.Brentner和Cox等对二维的圆柱绕流进行了仿真计算，所采用的大都是雷诺平均法［2-3］。2002年，Osamu Inoue为了研究均匀流中二维圆柱流噪声的产生和传播机理，采用了直接数值模拟的方法，但所计算的雷诺数只有150［4］。随着计算条件的提高，越来越多的人开始使用大涡模拟（LES）的方法预报流噪声，2004年，Tang用大涡模拟方法来获取圆柱绕流水动力数据，再用解FW-H方程的方法预报远场噪声［5］。

虽然大涡模拟的计算精度得到了很多学者的认可，但其所需的计算网格数量巨大，对于实尺度舰船噪声问题仍存在使用限制，而雷诺平均法（URANS）又存在难以准确捕捉湍流的问题。一种混合LES/URANS的方法被提了出来，即脱体涡方法（DES），这种方法在近壁区采用URANS模拟，而在远离壁面区域采用LES，网格数较小，且能够保证计算精度。预报辐射噪声有两种方法，一种是基于FW-H积分形式方程的解法，另一种用边界元法求解声学Helmholtz方程。用积分法求解FW-H方程的优点是它将声的产生和传播分别计算，计算量和计算格式要求相对较低，但也存在只能用于计算远场辐射和不能考虑结构和声学装置的影响等缺点。而边界元方法则在计算流激振动噪声方面有其独特的优势。江文成对比了FW-H积分法和边界元法在近场和远场的流噪声计算上的区别［6］。

为探寻一种保证精度、资源配置合理的计算方法，本文首先对圆柱的低马赫数下的气动噪声进行了数值模拟，采用不可压缩流动，对比了不同的流场仿真方法和声场预报方法的区别。分别采用大涡模拟、脱体涡模拟和雷诺平均法进行了圆柱流场仿真，对比了各种方法的差别，从中挑选适用于流噪声计算的流场仿真方法。流场计算后进行声场预报，使用了FW-H积分法和边界元法，对比了两种方法的差异。通过这些研究工作，本文的计算方法可为大尺度舰船流噪声预报提供支撑。

1　数学模型及计算方法

流体流动最基本的控制方程为Navier-Stokes方程（NS方程），可表示为如式（1）和式（2）形式

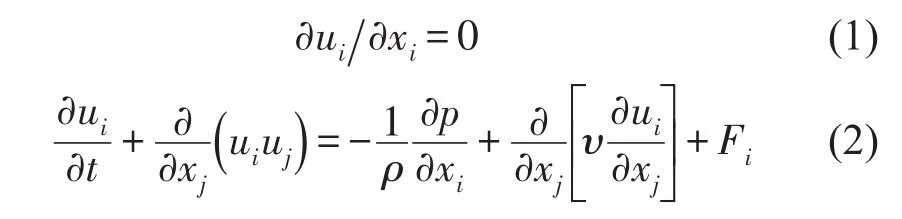
理论上流噪声分析和流场分析使用同样的控制方程，但由于声场和流场在尺度、能量上的差异，用流场控制方程求解声场物理量会非常复杂。为此Lighthill［7，8］提出声类比理论，Lighthill没有做任何简化及假设，直接对NS方程和连续性方程进行变换，得到非齐次波动方程

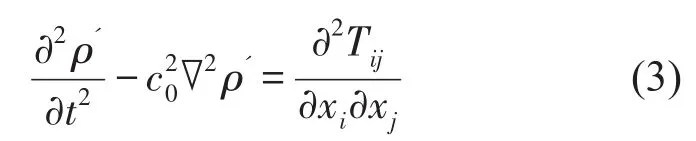
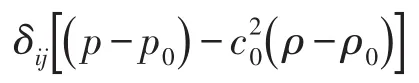
2　流场预报

预报气动噪声之前首先要对流场进行精确计算，CFD方法一般分为以下几类：大涡模拟（LES）、脱体涡模拟（DES）和瞬态雷诺平均法（URANS），几种方法的介绍如表1所示。

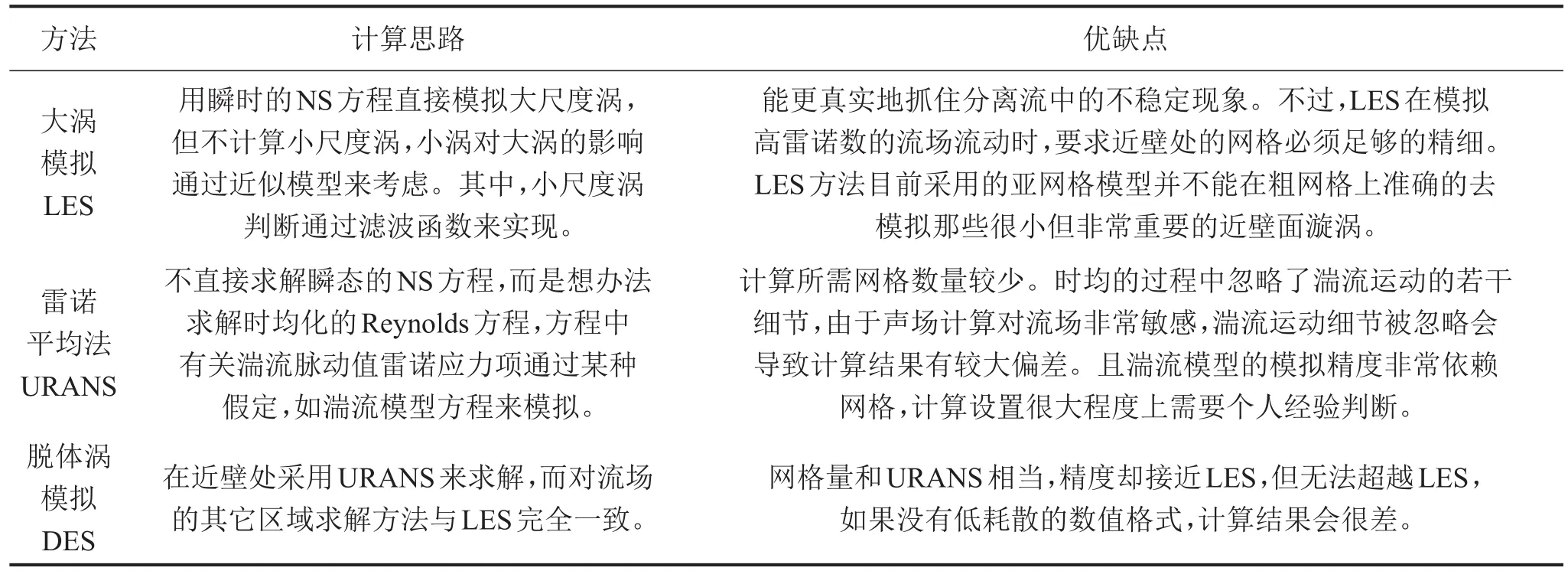
表1　流场仿真方法概述

具体的模型设置中，LES的亚格子应力模型采用动态的Smagorinsky-Lilly模型，这种模型可以考虑能量在亚网格上的转移，从而取得更好的模拟效果。URANS方程对NS方程进行平均，其中雷诺应力项需要用某种湍流模型进行假定，本文采用SST k-ω湍流模型，因为SST k-ω湍流模型采用Standard k-ω湍流模型求解近壁区域，采用k-ε湍流模型求解湍流区域，并且在两模型之间进行平滑过渡，因此SST k-ω模型较其它模型能更好地模拟近壁区流场，得到的结果也更加准确。DES模拟中除了最基本的DES模型外，还有DDES（Delayed DES）和IDDES（Improved Delayed DES）两种改进方法，DDES引入过渡函数，推迟RANS到LES的转换，从而解决了由于RANS到LES提前转换导致雷诺应力模化不足，产生网格诱导分离的问题；DDES是一种包含壁面LES的方法，它兼具DDES和LES壁面模型的特点，能够解决边界层附近“Log-Layer Mismatch”的问题，并且能够加快分离区RANS到LES的转换。

计算模型为直径D=19 mm的圆柱，其展向长度为10倍直径，即190 mm长。流场入口距圆心为5倍直径，平行流线方向两个面距圆心为5倍直径，出口距圆心为25倍直径。计算域如图1所示。边界条件：face 2、4、6为速度入口边界条件；face 5为压力出口边界条件；face 3为壁面边界条件，垂直于圆柱的两个面face 1和face 7设为对称面。

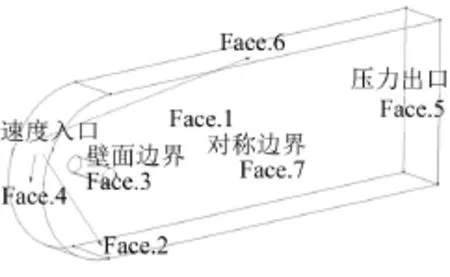
图1　几何模型及边界条件

入口条件采用速度入口，速度大小为69.19 m/s，流体介质为空气，马赫数为0.2，在该马赫数下可以不考虑流体的可压缩性。噪声计算之前，先用CFD计算圆柱绕流流场信息。流场计算过程中，先进行定常计算，定常计算的目的是为非定常计算提供一个稳定的流场，以便流动更好地收敛；再进行非定常计算。控制方程使用基于单元中心的有限体积法离散，其中对流项采用2阶迎风差分格式，扩散项采用中心差分格式；压力与速度的耦合使用PISO算法；离散得到的代数方程使用Guass-Seidel迭代求解。

典型计算域网格如图2所示，网格壁面进行了加密处理，在轴向进行了200层网格划分，由于使用不同计算方法时，壁面所需的网格数不同，所以进行了六套网格划分，划分的网格第一层网格高度分别为0.006 mm、0.015 mm、0.05 mm、0.09 mm、0.15 mm 和0.3 mm，对应的网格数分别为，760万、610万、486万、410万、378万和304万网格。

图2　圆柱网格示意图

首先进行网格验证计算，流场计算使用URANS、LES、IDDES三种计算方法，将这三种计算方法都应用于六套网格中。提取流场得到的升力系数频率，该频率即为周期性漩涡脱落的频率，再通过公式（4）得到St数；通过总阻力Fd和式（5）计算得到阻力系数Cd，对其取平均值得到-；引入描述网格壁面距离的无量纲参数y+，y+的表达式如式（6）所示，其中Δy表示离壁面的距离，这里指第一层网格高度，uτ是壁面摩擦速度是壁面切应力，μ是流体动力黏性系数，v是流体运动黏性系数，ρ是流体密度。试验［1］测得St数为0.2、为1.2，对比试验结果，做出St数和-Cd随圆柱壁面y+变化的规律分别如图3和图4所示。

图3　St数随y+变化曲线

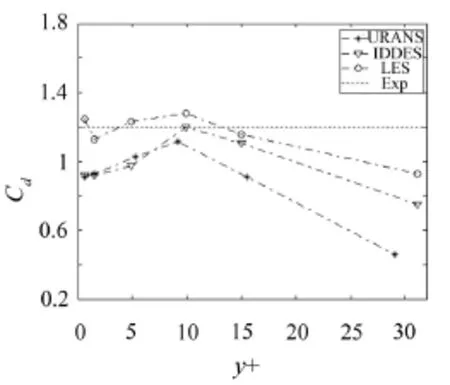
图4　随y+变化曲线

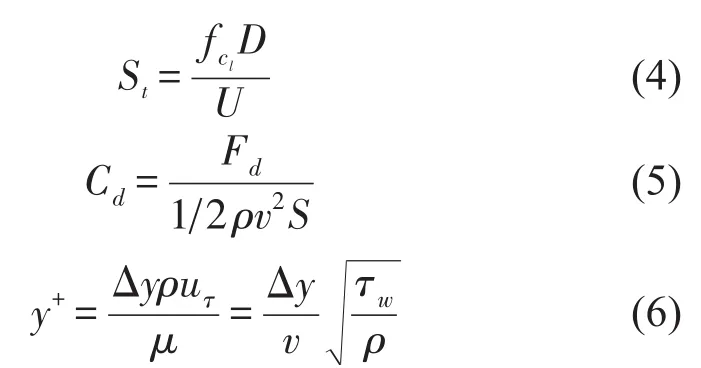
从图3和图4可以看出，使用LES计算时，在y+值小于1时才能得到最佳的计算结果，这是因为LES是基于滤波函数的，无法模拟比自身网格尺度更小的涡，所以如果壁面网格不够精细的话，LES就无法捕捉足够的流动，计算结果就会很差。另一方面，使用URANS和DES时，壁面y+值并不是越小越好，而是有一个最佳范围，由于两种模型都是使用SST k-ω湍流模型，所以均在y+值等于10左右能够得到最好的模拟效果。从文献［9］可知，流场中的壁面区域可划分为三个范围，分别是黏性底层、过渡层和对数律层，y+代表与壁面的无量纲距离，当y+＜5时，所对应的区域是黏性底层，此时的速度沿壁面法线方向呈纤细分布，流场为层流状态，如果在这些区域用湍流来模拟，预报结果将很差。所以使用DES或者URANS模型时，壁面y+值必须超过黏性底层，文献［9］给出的y+=5作为黏性底层的最外层，本文的计算中发现y+在10左右能取得较好的计算结果。这也说明使用DES进行流场仿真时，所需的网格数量要小于LES模型，如果模拟有许多弯曲壁面的模型，DES所需网格数量将大大减小。

网格验证计算后，分别采用URANS、DES、DDES、IDDES和LES结合最适应的网格进行流场仿真，将结果与试验结果对比，如表2所示。

表2　不同流场模拟方法计算的阻力系数和St数的最优结果与试验值对比（试验值St=0.2，=1.2）

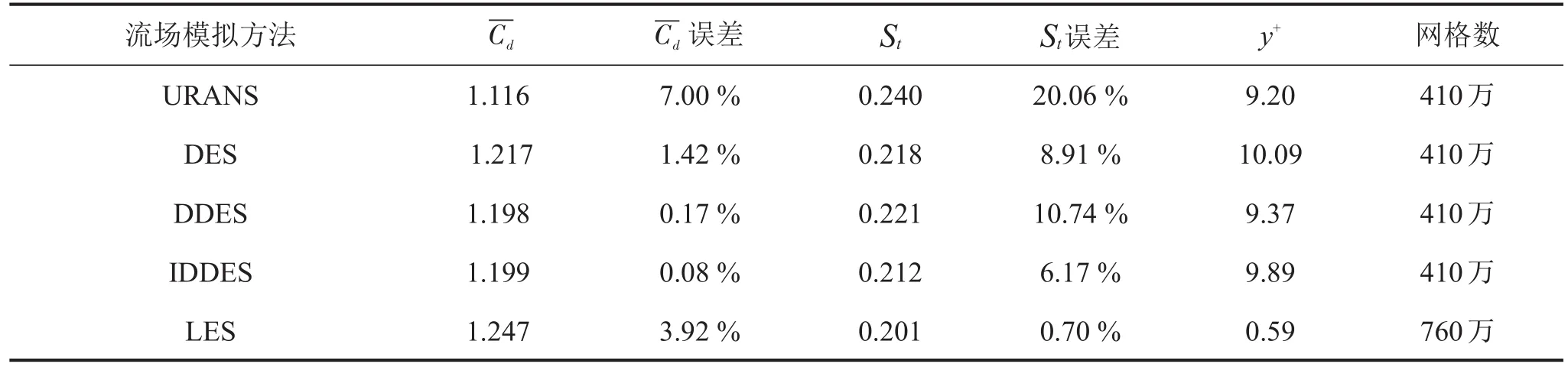
表2　不同流场模拟方法计算的阻力系数和St数的最优结果与试验值对比（试验值St=0.2，=1.2）

流场模拟方法URANS DES DDES IDDES LES -Cd -Cd误差Sty+ 1.116 1.217 1.198 1.199 1.247 7.00% 1.42% 0.17% 0.08% 3.92% 0.240 0.218 0.221 0.212 0.201 St误差20.06% 8.91% 10.74% 6.17% 0.70% 9.20 10.09 9.37 9.89 0.59网格数410万410万410万410万760万

对比表2中不同湍流模拟方法计算阻力系数和St数，LES方法模拟的涡脱落频率和试验值误差最小，而使用IDDES方法预报的阻力系数值和试验结果误差最小。综合而言，使用LES结合动态Smagorinsky-Lilly模型的方法预报的结果最为理想，频率和阻力的误差均在4%以下。IDDES模型和DDES模型模拟的阻力系数和试验误差很小，IDDES方法要优于DDES方法，DDES方法又优于DES法。使用URANS模型方法与其他方法相比，误差较大。

图5描绘了一个周期内4个阶段涡量云图，对于圆柱绕流问题，当流场雷诺数Re处于65到2×105之间时，尾流中会形成稳定的涡列，涡从圆柱表面脱落并一直延续至下游，在Re=90 000的条件下，形成的尾涡也会很不均匀。对比发现：用LES法得到的流场涡量云图非常清晰，不仅可以观察到尾涡交替性的脱落，也可以发现涡核逐渐发展、分离为几个涡，形成湍流的现象。而用URANS法得到的云图比较均匀，与实际的尾涡发展成极不均匀的湍流的情况不符。DES在近壁区使用雷诺平均应力方程，在远场使用大涡模拟，所以在近壁区涡量变化更接近URANS法，而远离壁面区域接近LES法，从涡量变化上来看，DES在壁面处可以观察到均匀的涡脱落，而远离壁面处则更接近LES的涡量场。

图5　圆柱径向截面涡量一周期变化云图

从流场预报来看，LES结合动态Smagorinsky-Lilly模型的方法能最真实、准确地模拟流场变化，但同时它所需的网格数量很大，圆柱表面y+值需要保证在1以下。而使用DES和URANS时，y+值取在10左右最为合适，其中IDDES方法计算的结果较好。所以进行流噪声预报时，流场预报可以采用LES方法和IDDES方法。

3　声场预报

流体流经圆柱时，会交替性地产生脱落的漩涡，同时在圆柱面上形成脉动的升力，这种脉动升力就是噪声形成的主要原因；此外，脱落的漩涡逐渐形成湍流，也会产生四极子噪声源。目前对流噪声的预报主要有两种途径：一种是基于FW-H积分形式方程的解法，另一种是先从CFD计算结果中获取声源场，再使用边界元法求解声学Helmholtz方程。两种方法均是基于Lighthill声类比理论，在流场模拟准确的基础上，本文对比两种方法的差异。

由Focus Williams和Hawkings提出的FW-H方程是一种非齐次的波动方程［10］，它可以通过直接推导流体的连续性方程和Navier-Stokes方程获得，FW-H方程有如下形式

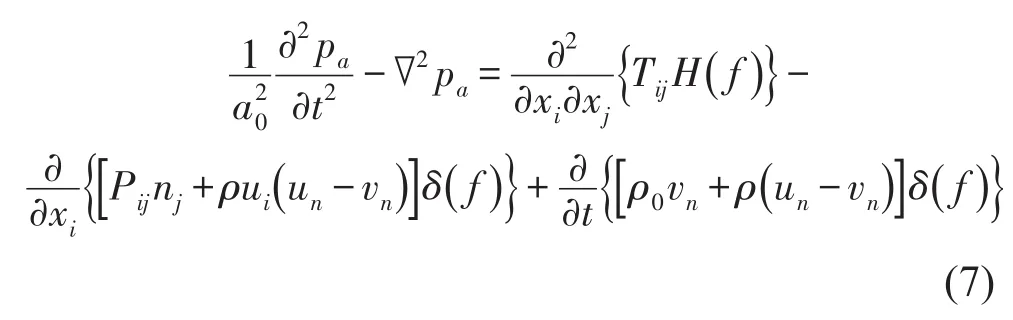
式中ui代表流体在xi方向的速度分量；un代表流体在 f=0面上的法向速度分量；vi代物面速度在xi方向的速度分量；vn代物面速度在 f=0面上的法向分量；δ（f）代表狄拉克函数；H（f）代表Heaviside函数。如果假设流动是在自由空间中的并且声源和接受者之间没有障碍，则方程可以用积分法解析的求解出来，完整的解析解包括面积分和体积分。面积分代表单极子、偶极子和面上四极子声源的作用，体积分则表示声源面外部四极子源的作用。本例中流动是亚音速的，体积分可以忽略。时域FW-H积分解可用时域形式求解出来。

边界元方法同样是以Lighthill方程为控制方程，对公式（3）进行傅里叶变化，可以得到非齐次的Helmholtz方程，并代入基本解。本例的流场是用不可压缩流体计算，认为壁面压力脉动pCFD并没有计算得到壁面声压pa，任一点声压的表达式为

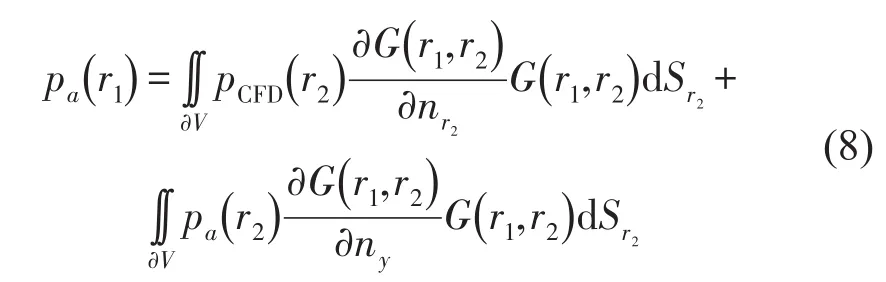
其中G（r1，r2）是Helmholtz方程的基本解，pCFD（r2）是流场计算的表面脉动压力，pa（r2）是表面声压。此时，要首先解决边界上的声压问题，才能进一步进行边界元求解。得到了声压的表达式后，用边界元对边界面进行网格离散，将型函数Nj代入式（8），最终得到边界元离散形式的解为

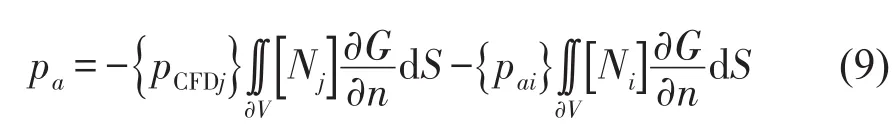
通过式（9），就可以通过先求得壁面的声压值，再求解空间任一点的声压值。

对于CFD计算得到的流体脉动压力数据，如果要采用FW-H积分法预报辐射噪声，则直接打开Fluent的噪声计算模块计算即可，方法方便快捷。如果要采用边界元求解辐射噪声，还需将流体数据导入声学边界元计算程序，并且要划分边界元网格，但在用边界元求解时可以考虑声源与接受者之间存在障碍的情形，并且可以计算流激振动噪声。如图6所示取距圆柱正上方128 D处为监测点，计算值如表3所示，该点处的总声压级试验结果［1］为100 dB，不同流场得到的声压曲线对比如图7所示，积分法和边界元方法的对比如图8所示。

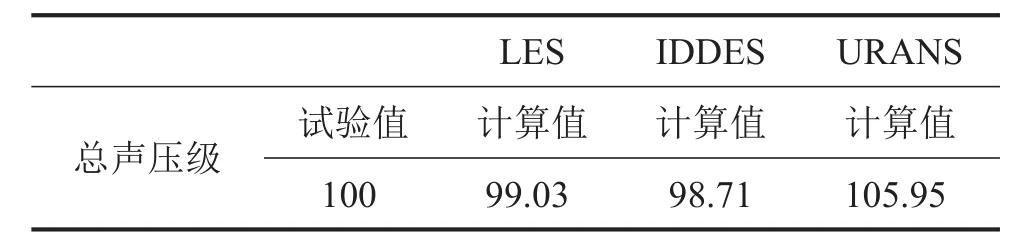
表3　监测点总声压级与试验值对比/dB

图6　监测点示意图

在表3监测点（0，128 D）总声压级的对比中，LES和试验结果最为接近，IDDES次之，URANS结果最差。从图7中的LES、IDDES和URANS计算声压值以及试验测量的声压值对比发现：基于LES的辐射噪声预报结果与试验结果最为接近；基于IDDES的辐射噪声预报结果和和LES相差不大，只是峰值频率与试验结果稍有偏差。URANS法无法捕捉到峰值频率，且计算得到的声压级频谱曲线非常光顺，这是因为URANS方法的局限性，脉动量都是通过湍流模型求得的原因。综合而言，LES结合动态Smagorinsky-Lilly模型方法预报的流噪声最为准确；IDDES方法也比较准确，但由于其网格要求并不严格，在计算量方面占有优势；而URANS方法由于将流场的脉动量进行了均化，而代表脉动的雷诺应力项只能通过湍流模型捕捉，所以预报流噪声结果较差。噪声计算方法方面，从图8中可以看出，积分法和边界元法计算结果基本一致。

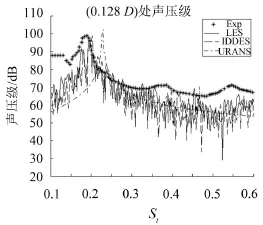
图7　不同流场模型预报辐射噪声对比

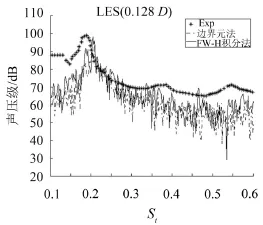
图8　积分法和边界元法对比

4　结语

本文分别用大涡模拟（LES）、脱体涡模拟（DES）和瞬态雷诺平均法（URANS）的方法模拟了三维圆柱绕流流场，并分别用FW-H积分法和边界元法计算了远场辐射噪声，对比各算例的计算结果，得到如下结论：

（1）使用LES要保证壁面网格无量纲高度y+值小于1，因为LES是基于滤波函数的方法，y+值大于1会导致网格尺度太大，从而无法模拟足够精细的流动。使用DES结合SST k-ω湍流模型时，y+取在10左右的范围较合适，因为y+＜5处于壁面黏性底层，此时流动全为层流，湍流模型不起作用，所以壁面网格并非越精细越好。

（2）流场预报方法中，LES结合动态Smagorinsky-Lilly模型的方法计算的辐射噪声和试验结果最为接近，但网格量较大；DES法中的IDDES计算的辐射噪声结果也较为准确，在保证计算精度的前提下可有效降低网格数量；URANS方法预报结果误差较大。声辐射预报方法中，FW-H积分法和边界元法预报远场直发声结果基本相同。

［1］REVELL J D，PRYDZ R A，HAYS A P.Experimental study of aerodynamic noise vs drag relationships for circular cylinders［J］.Aiaa Journal，1977，16（9）：889-897.

［2］BRENTLNER K S，COX J S，RUMSEY C L，et al. Computation of sound generated by flow over a circular cylinderanacousticanalogyapproach［C］//Second ComputationalAeroacoustics（CAA） Workshopon Benchmark Problems.NASA.1997.

［3］COX J S，CHRISTOPHER L.Computation of sound generated by viscous flow over a circular cylinder［C］// Proceedings oftheASME/JSME/IMechE/CSME/IAHR4th International Symposium on Fluid-Structure Interactions，Aeroelasticity，Flow-Induced Vibration&Noise.1997.

［4］INOUE HATAKEYAMA.Sound generation by a twodimensional circularcylinderinauniformflow［J］. Journal of Fluid Mechanics，2002，471（1）：285-314.

［5］TANG K F.Numerical simulation of flow-induced noise by means of the hybrid method with LES and aeroacoustic analogy［D］.University of Siegen，Germany，2004.TANG K F.

［6］江文成，张怀新，孟堃宇.基于边界元理论求解水下潜艇流噪声的研究［J］.水动力学研究与进展，2013，28（4）.

［7］LIGHTHILL M J.On sound generated aerodynamically.I. general theory［J］.Proceedings of the Royal Society A Mathematical Physical&Engineering Sciences，1952，211（1107）：564-587.

［8］LIGHTHILL M J.On sound generated aerodynamically. II.turbulence as a source of sound［J］.Royal Society of London Proceedings，1954，222（1148）：1-32.

［9］FLUENT Inc.Fluent User's Guide，Fluent Inc，2003.

［10］WILLIAMS J E F，HAWKINGS D L.Sound generation byturbulenceandsurfacesinarbitrarymotion［J］. Philosophical Transactions of the Royal Society A Mathematical Physical&Engineering Sciences，1969，264（1151）：321-342.

ComparativeStudyontheFlowFieldandAcousticFieldSimulation forNoisePredictionInducedbytheFlowaroundaCylinder

ZHANG Han-qin，CHENMing，SUN Guo-cang
（Wuhan 2nd Ship Design and Research Institute，Wuhan 430205，China）

Lighthill acoustic analogy method is used to predict the noise induced by the flow around a three dimensional cylinder.Firstly，the flow field of sound source area is predicted by large-eddy simulation（LES），detached-eddy simulation（DES）and Transient Reynolds-average method（TRAM）respectively.The proper methods to simulate the flow field are selected via comparing the contours of vorticity and pressure.Secondly，the FW-H integral equation method and BEM method based on Lighthill acoustic analogy equation are used to predict the far-field noise，difference of these methods is analyzed by comparing their results with Revell's experimental data.It is shown that the flow field simulation result of LES has a best agreement with the experimental data，IDDES method can effectively reduce the number of grid of the flow field with the precision guaranteed.TRAM can yield large errors.FW-H integral equation method and BEM method can essentially yield the same results in predicting radiation noise.

acoustics；flow-induced noise；LES；DES；Lighthill acoustics analogy

O422.6

ADOI编码：10.3969/j.issn.1006-1335.2016.03.006

1006-1355（2016）03-0026-06

2015-11-17

国家自然科学基金资助项目（51409199）

张翰钦（1992-），男，江西省南昌市人，硕士生，主要研究方向为水下结构物流噪声。E-mail：hackinzhq@sina.com