单群的点传递图的GI-性质

陈 静, 曲斯瑶

(1. 福州大学离散数学与理论计算机科学研究中心， 福建 福州　350003; 2. 湖南第一师范学院数学与计算科学学院， 湖南 长沙　410205)



单群的点传递图的GI-性质

陈 静1, 2, 曲斯瑶2

(1. 福州大学离散数学与理论计算机科学研究中心， 福建 福州350003; 2. 湖南第一师范学院数学与计算科学学院， 湖南 长沙410205)

针对点传递图的同构问题， 类似于Babai关于Cayley图为CI图的充分必要条件， 给出了点传递图为GI-图的判别准则， 并研究了单群的点传递图的GI-性质.

点传递图； 单群； 陪集图； GI-图

0　引言

设Γ是一个图, V(Γ)、 E(Γ)、Arc(Γ)以及Aut(Γ)分别表示图Γ的顶点集、 边集、 弧集以及全自同构群. 令G是Aut(Γ)的一个子群, 如果G传递地作用在图Γ的顶点集、 边集或弧集上, 则分别称图Γ是G-点传递的、 G-边传递的或G-弧传递的. 如果Aut(Γ)在Γ的顶点集、 边集或弧集上是传递的, 则分别称图Γ是点传递、 边传递或弧传递的.

图的同构问题的判断, 是图论研究以及决定图的同构类的基本问题. 对于Cayley图, Cayley图同构问题研究起源于1967年Adam提出的一个猜想: 每个有限循环群都是DCI-群. 在过去的几十年里, 该问题得到了广泛的研究, 参见文献[1-6]. 由于很多点传递图并不是Cayley图, 下一步的研究对象就由Cayley图转移到点传递图上, 参见文献[7]. 对于点传递图, 希望能通过其点传递自同构群来判断它们是否同构, 即通过群G的性质判断两个G-点传递图是否同构.

一个G-点传递图Γ=Cos(G, H, HSH)称为G的GI-图, 如果对于任意的图Σ=Cos(G, H, HS′H), 当Γ≅Σ时, 存在τ∈Aut(G)使得Hτ=H, (HSH)τ=HS′H. 其中,GI表示群自同构诱导的图同构. 特别的, 当H=1时, Γ是G的Cayley图, 如果它是G的GI-图, 则被称作G的CI-图.CI-图在过去几十年得到了广泛的研究. 类似于Babai关于Cayley图成为CI-图的充分必要条件的研究, 本文讨论了G-点传递图成为G的GI-图的充要条件, 研究了单群的点传递图的GI-性质.

1　GI-图的判别准则

设G是一个群, H为G的子群, S为G的子集, 定义群G关于H和S的陪集图Γ, 其中顶点集为V=[G:H], 对任意的Hx, Hy∈[G:H], Hx与Hy邻接当且仅当yx-1∈HSH, 记作Γ=Cos(G, H, HSH). 当H=1时, Γ=Cos(G, H, HSH)即为Cayley图Cay(G; S). 在此, 给出陪集图的一些性质.

性质1

2) G传递地作用在点集[G:H]上, 作用的核恰好是H在G中的核, 即包含在H中的G的极大正规子群;

3) Γ是连通的当且仅当〈H, S〉=G;

4) Γ是G-弧传递的当且仅当存在元素g∈G, 有g2∈H, 且HSH=HgH.

引理2设Γ=(V, E)是群G的点传递图， 则当且仅当Aut(Γ)中所有置换同构于G的子群在Aut(Γ)中都是共轭的, Γ是G的GI-图.

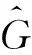
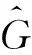
这一准则类似于由Babai和Parsons得到的关于Cayley图为CI-图的判断准则. GI-图的判断准则在Cayley图同构问题的研究中起着极其重要的作用, 参见文献[8].

2　单群的点传递图的GI-性质

引理3设G是有限单群， 则G的外自同构群都是可解的.

定理1设G是有限非阿贝尔单群, Γ是一个G-点传递图. 若Aut(Γ)≤Aut(G), 则Γ是群G的GI-图.

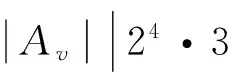
定理2令G是有限非阿贝尔单群, Γ是连通的三度G-对称图, 则：

1) (G,Aut(Γ))是(A7, A8)、 (A7, S8)、 (A7, Z2.A8)、 (A15, A16)、 (GL4(2), AGL4(2))之一;

2) Γ是G的GI-图.

证明令X=Aut(Γ). 因为Γ是连通的G-弧传递图, 所以X=GXv, 其中Xv是点v∈V(Γ)的稳定子群. 若G不是X=Aut(Γ)的正规子群. 由文献[11]中的定理7.1.3可知, (G,Aut(Γ))是(A7, A8)、 (A7, S8)、 (A7, Z2.A8)、 (A15, A16)、 (GL4(2), AGL4(2))之一. 下面假设G是X=Aut(Γ)的正规子群.

[1] ALSPACH B. Isomorphisms of Cayley graphs on abelian groups[M]// HAHN G, SABIDUSSI G. Graph symmetry: algebraic methods and applications. [S.l.]: Springer, 1997: 1-22.

[2] BABAI L. Isomorphism problem for a class of point-symmetric structures[J]. Acta Math Acad Sci Hungar, 1977, 29: 329-336.

[4] GODSIL C D. On the full automorphism group of a graph[J]. Combinatorica, 1981, 3(1): 243-256.

[5] GODSIL C D. On Cayley graph isomorphisms[J]. Ars Combin, 1983, 15: 231-246.

[6] SOMLAI G. Elementary abelianp-groups of rank 2p+3 are not CI-groups[J]. Journal of Algebraic Combinatorics, 2011, 34(3)： 323-335.

[7] DOBSON E. Isomorphism problem for metacirculant graphs of order a product of distinct primes[J]. Canadian Journal of Mathematics, 1998(6): 1 176-1 188.

[8] LI C H. On isomorphisms of finite Cayley graphs-a survey[J]. Discrete Mathematics, 2002, 256(1/2): 301-334.

[9] TUTTE W T. A family of cubic graph[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1947, 43(4): 459-474.

[10] TUTTE W T. On the symmetry if cubic graphs[J]. Canad J Msth, 1959, 11: 621-624.

[11] LI C H. Isomorphisms of finite Cayley graphs[D]. Perth: The University of Western Australia, 1997.

(责任编辑： 林晓)

The GI-properties of the vertex-transitive graphs of simple groups

CHEN Jing1, 2， QU Siyao2

(1. Center for Discrete Mathematics and Theoretical Computer Science, Fuzhou University, Fuzhou, Fujian 350003, China;2. College of Mathematics and Computer Science, Hunan First Normal University, Changsha, Hunan 410205, China)

On the isomorphism problem of the vertex-transitive graphs, we give the criterion for a vertex-transitive graph to be a GI-graph, analogous to the conditions for a Cayley graph to be a CI-graph given by Babai. On basis of this, we attack the GI-properties of the vertex-transitive graphs of simple groups.

vertex-transitive graphs; simple groups; coset graphs; GI-graph

10.7631/issn.1000-2243.2016.01.0017

1000-2243(2016)01-0017-03

2015-08-31

陈静(1983-)， 讲师， 主要从事图论的研究，chenjing827@126.com

国家自然科学基金资助项目 (11326057， 11501188)

O157.5

A