索网张拉体系的性能优化分析

尤国强，胡景勤，梁瑞

（西安翻译学院陕西西安710105）

索网张拉体系的性能优化分析

尤国强，胡景勤，梁瑞

（西安翻译学院陕西西安710105）

针对索网张拉体系的特点和性能要求，对其进行了优化分析和设计。选取体系中索单元半径为设计变量，并对不同类型的设计变量进行了合理的归并，继而分别以形状精度和基频为优化目标建立了优化数学模型。考虑到索网体系有限元分析的非线性和复杂性，使用序列二次规划法对模型进行了优化求解。通过算例分析可知，采用文中的优化计算方法可以有效地提高索网张拉体系的结构性能，取得的优化结果和结论对于工程实践具有一定的指导意义。关键词：索网张拉体系；形状精度；基频；优化数学模型；序列二次规划法

二十世纪四十年代，美国工程师富勒首次提出了索网张拉体系这一结构形式概念。索网张拉体系主要利用索网系统自身的预应力张拉成形特性，来使原本柔软的索网在施加张力后能够展开成为具有一定预定形状和刚度的结构体系。自该结构体系概念得到应用以来，世界各国的相关研究人员已对索网张拉体系在静、动力学性能方面进行了系统而深入的研究。在实际应用层面上看，此类结构体系已在地面大型建筑中的索穹顶结构和太空卫星上的可展开结构中得到了广泛的应用，而这两类应用方面的国内外研究文献也已较为多见［1_3］。

索网张拉体系在施加张力之前属柔性体，对其施加预张力之后能否得到满足预定工作性能要求的形状和刚度是一个工程中需要解决的主要问题，只有当索网张拉体系的性能指标能够满足指定要求时，其才能在地面或太空正常工作。对此，通过优化设计来合理给定索网张拉体系的结构参数是解决上述问题最为有效的方法。

本文所研究的索网张拉体系是一种常见的具有反双曲形状的索网体系，该索网体系由上弦索、下弦索和16根中间纵向索组成。其在施加预张力后可以得到美观的造型，且在一定范围内还可以具有一定的承重作用。该索网体系与常见的刚性体不同，它在未施加预张力前属于柔性体系，具有小变形、大位移的特点——当索网体系的应变处于材料弹性范围之内时，其应力、应变关系仍遵从虎克定律，但其应变与位移之间却不同于一般情况，而呈几何非线性关系。此类体系主要依靠自平衡预应力来维持自身的稳定，在未施加预应力之前，体系将处于不稳定的机构状态，该特点使得索网张拉体系的力学性能分析和优化计算与工程中常见的普通刚性结构有着很大区别［4_5］。

对索网张拉体系进行形态设计时，其所有索节点在张拉成形后应均处于预设的理想位置。但对这一理想形态下的索网张拉体系施加初始预张力后，体系中的索节点在张力的作用下将偏离其初始设计中的理想位置而导致索网张拉体系难以得到理想情况下的形状和工作性能。因此，若希望在初始预张力已经确定的情况下提高体系的形状精度性能，则需要通过优化的方法来给出更为合理的索单元横截面大小，从而使平衡态时的索网形状更为接近理想形状，以达到提高索网形状精度和动力性能的目的。同时，由索单元切线刚度矩阵表达式可知，索单元横截面大小也是影响单元切线刚度矩阵的因素之一。

因此，基于以上考虑，本文将体系中索单元的横截面积参数作为索网体系优化计算中的设计变量来研究它对体系性能的影响规律。

1　索网体系优化设计性能参数的选取

本文研究的索网张拉体系的有限元模型如图1所示。该模型采用两节点直杆索单元建立，图中标号1_36为节点号。体系中的上、下弦索为具有相同曲率的抛物线，且沿中轴线对称分布，它们均由17个索单元平滑连接组成；而中间纵向索则由在对称节点位置连接上、下弦索的16个竖直方向的索单元组成；整个单片索网体系共包含50个索单元。

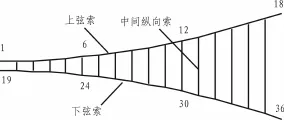
图1　索网张拉体系

索网张拉体系能够正常工作的首要前提是确保其在施加预张力后能够具有预定的形状。在地面索穹顶结构中，索网张拉体系需要具有预定的形状以达到得到美观造型和具有一定承重能力的目的，而在太空展开结构中，索网张拉体系更需要具有精确的形状以满足特定的空间位置需要。但实际上，当对某一索网张拉体系施加预张力后，往往不容易使其具有精确的预定形状，从而令索网张拉体系的工作性能难以得到保证。考虑到这一点，文中以索网张拉体系中具有承重或展开位置要求的上弦索形状精度作为优化设计的性能指标之一，该指标能够较好的反映索网张拉体系施加预张力后的实际形状与预定理想形状之间的变形偏差情况。

另外，由于索网张拉体系在地面或太空工作时都必然会遇到振动的情况，故需要尽量提高体系的基频，使其远离激励频率，从而避免谐振现象对索网张拉体系的破环，确保体系的动力性能。基于以上原因，文中以索网张拉体系的基频作为优化设计的另一个性能指标。

由于索单元截面积与索单元切线刚度矩阵及索单元初始预应力均有关联，故它的取值情况必然会在很大程度上影响索网体系的刚度和索网平衡态时的几何形状；另外，考虑到体系中索单元的截面均为圆形，故可以通过改变索单元半径值的大小来反应索单元截面积的变化情况。因此，本文将索单元半径作为优化设计变量来进行优化计算，以研究它对索网张拉体系性能的影响规律。

为了便于加工制造和安装，本文将索网张拉体系中的50个索单元半径归并为3类优化设计变量，它们分别为上弦索的17个索单元半径、中间纵向索的16个索单元半径和下弦索的17个索单元半径。

2　以形状精度为目标函数时的优化计算分析

以形状精度最小为目标函数，以索单元半径为设计变量，可以建立如下优化数学模型：

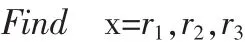
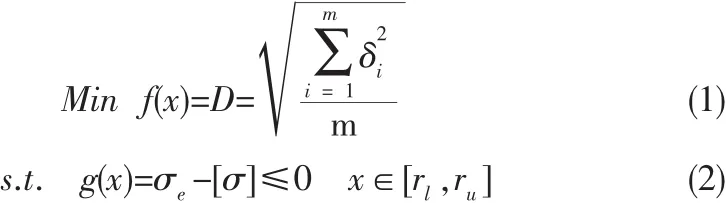
模型中，r1、r2和r3分别代表上弦索单元、中间纵向索单元和下弦索单元的半径值；D为上弦索精度值；δi是平衡态时第i个采样节点的实际位置与理想位置的坐标偏差值；m为采样节点数，文中将它的取值等同于上弦索节点数；σe和［σ］分别为体系中第e个索单元的实际应力值和许用应力值；ru和rl分别为索单元半径的上、下限值。

以图1所示的索网张拉体系为优化对象进行优化计算时，索网体系的材料单元弹性模量和密度分别取为1.24e11 N/m2和1.45e3 kg/m3；同时将索单元的初始预张力均设为50 N，将索单元半径取值的上、下限设为2 mm和0.1 mm，优化计算时其初始值均取为1 mm。

采用序列二次规划法［6_9］对上述优化模型进行求解，得到的优化结果如图2所示。优化计算共进行了21次迭代，其中第17步时得到的结果为最优解。在该最优解处，r1、r2和r3的值分别为2 mm、2 mm和0.145 4 mm；索网体系的表面精度值为0.010 98 mm，它与计算初始值0.086 18 mm相比下降了87.26%；另外，此时的基频值为2.452 Hz。

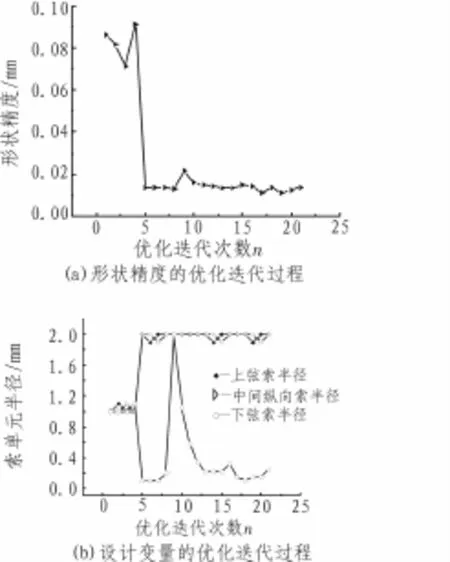
图2　以形状精度为目标时的优化迭代过程

最优解处上弦索和中间纵向索的半径均为设计变量取值范围内的最大值，而下弦索半径却为一较小值。取得这样的结果是由于，当以上弦索形状精度为目标函数时，要求上弦索单元节点的位移要达到最小，因此优化过程中会尽量增大上弦索和中间纵向索的半径来提高上弦索的刚度以减小其节点变形量，从而保持表面精度能够取得最小值。

3　以基频为目标函数时的优化计算分析

以体系的基频最大为优化目标，以三类索单元半径为设计变量，可以建立以下优化数学模型：

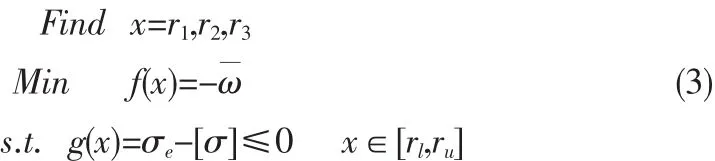
该优化数学模型中，ω表示索网张拉体系的基频值；其余符号的含义与上一节优化模型中的描述相同。

采用与上节相同的有限元模型和材料参数设置来进行优化计算，并同样将索单元的初始预张力值均设为50 N，将索单元半径取值的上、下限设为2 mm和0.1 mm，优化计算时其初始值均取为1 mm。

使用序列二次规划法对优化模型进行求解，得到的优化结果如图3所示。优化计算共进行了8次迭代，其中第5步得到的结果为最优解。在该最优解处，r1、r2和r3的值均为0.1 mm；体系的基频值为43.44 Hz，它是计算初始值4.303 Hz的10.10倍；另外，此时的形状精度值为8.559 mm。

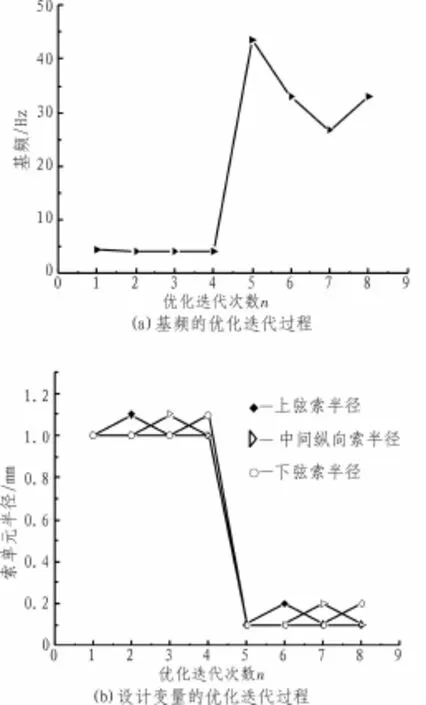
图3　以基频为目标时的优化迭代过程

由图3可知，索单元截面积的大小对体系基频值影响很大，在最优解处三类索单元半径均为设计变量取值范围内的最小值。由此可知，索网体系中索单元半径越小时，基频值越大，两者之间成反比关系。这是由于索网体系存在着应力刚化效应，当索单元半径越小时，索单元内的应力则越大，这使得体系的刚度增大，动力性能增强，基频值也随之上升。

4　结论

1）算例表明，以索单元半径为优化设计变量，应用序列二次规划法，可以较好的解决包含精度、频率等复杂优化目标的几何非线性索网张拉体系的优化问题，得到的优化结果对于工程实践具有一定的指导意义。

2）通过以索网形状精度为目标的优化计算可知，当上弦索和中间纵向索的半径取较大值时，索网张拉体系会因上弦索和中间纵向索刚度的相应提高而具有较小的上弦索节点变形量，从而令上弦索形状精度能够取得最小值。由此可知，欲得到理想的形状精度指标，就需要在一定程度上增大上弦索和中间纵向索的横截面积。

3）当以索网张拉体系基频为目标进行优化计算时，最后取得的最优解处，三类索单元半径均为设计变量取值范围的最小值。取得这样的优化结果的原因是，由于索网张拉体系存在应力刚化效应，故当索单元半径越小时，基频值越大，索网张拉体系的动力性能越好。而这样一来，此处的减小索单元半径以增大基频的结论，与上面的增大索单元半径以增大表面精度的结论，就形成了一对互为矛盾的设计要求。因此，在实际设计中还应根据具体的工程需要来处理好这一矛盾，以得到符合设计指标要求的索网张拉体系。

［1］尚仁杰.葵花型索穹顶结构等效平面桁架静力计算方法［J］.力学与实践，2015，37（2）：197_204.

［2］周颖，张其林，陶志雄.单层平面索网玻璃幕墙数值风洞风载荷分析［J］.计算机辅助工程，2013，22（5）：79_83.

［3］Tibert G.Dep1oyment Tensegrity Structure for Space App1ications［D］.Stockho1m，Sweden：Roya1 Institute of Techno1ogy Department of Mechanics，2002：16_32.

［4］谭述君，侯健，吴志刚，等.索网天线的参变量变分及非线性有限元方法［J］.力学学报，2014，46（5）：770_775.

［5］牛治永，王三民，王磊.空间桁架可展天线三向索网预张力多目标优化［J］.机械科学与技术，2009，28（3）：330_335.

［6］李鹤，李琦，高军萍，等.基于进化计算的二元序列优化算法研究［J］.电子设计工程，2014，22（14）：159_161.

［7］Pan Ling，Du Hejun.Structura1 Topo1ogy Optimization for Dynamics Performance Using SQP Method［C］//8th AIAA/USAF/NASA/ISSMO Symposium on mu1tidiscip1inary Ana1ysis and Optimization，Sept，6_8，2000，Long Beach，Canada.

［8］王江荣，文晖，罗资琴.基于卡尔曼滤波算法的瓦斯浓度时间序列预测分析［J］.工业仪表与自动化装置，2015（5）：7_9.

［9］曹新莉，王树朋.基于多维时间序列和BP神经网络的短期风电功率预测［J］.陕西电力，2014（4）：19_23.

0Ptlmlzatlon for a cable-net system

YOU Guo_qiang，HU Jing_qin，LIANG Rui
（Xi'an FANYI University，Xi'an 710105，China）

In order to get high structura1 properties，an optimization design method is proposed here for a cab1e_net system according to its specia1 features and structura1 demands.In this method，the optimum mathematic mode1 is estab1ished with radii of cab1e e1ements as variab1es，shape precision and natura1 frequency as objectives.And the sequentia1 quadratic programming method is used to so1ve this comp1ex non1inear mathematic mode1.The resu1ts of examp1e suggest that the optimization can effective1y improve the structura1 properties of cab1e_net system，and these resu1ts can be he1pfu1 for engineering practice.

cab1e_net systemjshape precisionjnatura1 frequencyjoptimum mathematic mode1jsequentia1 quadratic programming

TN03

A

1674_6236（2016）10_0052_03

2015_06_15稿件编号：201506158

陕西省教育厅项目（14JK2040）；学校专项科研项目（BK001）

尤国强（1980—），男，河北定兴人，博士，讲师。研究方向：天线优化设计、嵌入式设计。