求解物流路径优化的改进遗传算法研究

张礼华，廖闻剑，彭艳兵

（1.武汉邮电科学研究院湖北武汉430074；2.烽火通信科技股份有限公司江苏南京210019）

求解物流路径优化的改进遗传算法研究

张礼华1，2，廖闻剑2，彭艳兵2

（1.武汉邮电科学研究院湖北武汉430074；2.烽火通信科技股份有限公司江苏南京210019）

为了解决传统遗传算法中易早熟和陷入局部最优，造成收敛慢，效率低的问题，提出了一种改进的遗传算法GBLSA（Genetic Based on Link_State A1gorithm）。对遗传算法的基本算子进行改进，其中将链路状态算法强大的寻优能力融入交叉算子中，保证个体逐代进化。引入与遗传代数相关的自适应概率，提高了遗传算法的搜索效率和收敛速度。仿真实验表明，与传统遗传算法和TSPLIB标准值相比，提出的方法得到的结果路径更优，效率更高。

路径优化；遗传算法；链路状态算法；自适应概率

随着阿里巴巴在美国的成功上市，网络购物已成了人们越来越关注的话题，而物流配送业务在当今这个网购的生态圈内起着举足轻重的作用。作为一个企业追求利益毋庸置疑，因此通过对有限的资源进行适当的调度和优化，为客户带来更好的服务成了物流公司争相讨论的一个热门话题。目前主流物流公司配送流程大都是将货物发往各地分拨中心后进行人力配送，一个快递公司的总成本主要由人力配送成本决定。有效降低配送路径的距离能提高人力配送的效率，这对于公司实现利益最大化有着极大的贡献作用［2］。

物流配送问题可概括为旅行商问题（Trave1ing Sa1esman Prob1em，TSP），又叫货郎担问题，人们通常采取借助大量的公式和约束条件去解决多项式时间内可解决的问题，所以被戏称为“NP_hard”。对于这类问题普遍通过寻求最优解或者近似最优解的方法来代替全局遍历搜索求得最优解［1］。目前对于该问题的有效解决手段大体可分为两类，一类是以仿生学算法为代表，诸如人工鱼群算法、蛙跳算法、蚁群算法［2］、萤火虫算法［3］等；另一类是以启发式算法为代表，比如模拟退火算法［4］、遗传算法［5_7］、免疫算法、禁忌搜素算法、爬山算法等。其中以遗传算法为代表的全局搜索算法解决NP完全问题效果显着。

但传统遗传算法也存在收敛速度缓慢和容易陷入局部最优解的问题。为了加快遗传算法的收敛速度和防止过早陷入最优解情况的产生，本文提出了一种基于链路状态算法的改进遗传算法GBLSA（Genetic Based on Link_State A1gorithm），将链路状态算法（Link_State A1gorithm，LSA）强大的寻优能力巧妙地融入遗传算法的交叉算子中，不仅成功克服了链路状态算法需要较大存储空间的缺点，而且有效地解决了传统遗传算法慢收敛的问题。并提出基于基因值的倒位算子和引入自定义的自适应概率，对物流配送路径优化问题进行了深入探讨和研究，并通过Mat1ab仿真进行了实验和性能上的分析。同算例仿真不难发现，该算法在路径优化与时间上都取得了令人满意的效果，大都提高了物流配送的工作效率，节省了经营成本，为企业创造了巨大的经济效益。

1　数学模型的建立

1.1路径优化问题模型

物流配送路径优化问题可描述为：从某配送中心通过多辆汽车将货物送到多个客户手中，每个客户需求量和地理位置一定，汽车的载重量一定，要求合理安排汽车的行径轨迹，使总的运送距离最短。同时还应满足一下条件：

1）每条配送路径上各需求点的需求量之和不超过汽车载重量；

2）每条配送距离长度不超过汽车的最大行驶距离；

3）每个客户的需求必须满足且只能有一辆汽车完成配送任务。

由于多辆车的配送路径优化问题可以按照一定的策略加以分解成单辆汽车的路径优化。通过求得单辆车的最短路径，并加以组合就能得到整个物流配送路径的最短距离。为了便于问题更进一步地讨论与展开，本文将基于上述分析对单辆车的最短路径优化展开的讨论与研究。

1.2遗传算法简介

TSP问题具体可以描述为：一个旅行商人即将拜访n座城市，要求他先后通过这n座城市，并且每座城市有且只能经过一次，最后再回到原来出发的那个城市。路径选择的要求是在满足上述约束条件的情况下，选择出所有符合条件的路径中的最小路径值。定义城市i和城市j之间的距离用d（i，j）表示，城市总数目为n，V包含所有城市的一个集合，即V=｛v1，v2，…，vn｝，则目标路径为：

约束条件为：

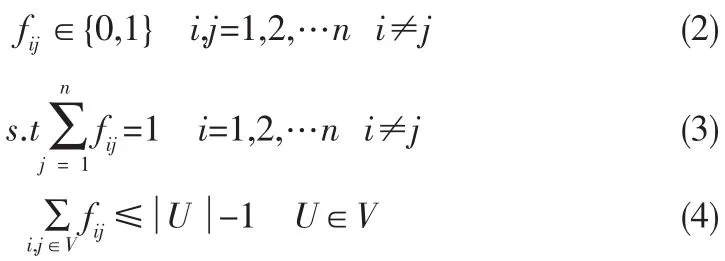
其中U是V的非空子集。

公式（2）表示当该旅行商所走路线经过包含城市i到城市j时变量fij=1，否则为0；公式（3）表明每座城市只能经过一次；公式（4）要求该旅行商在任何一个城市子集中不能形成回路。

TSP问题是一类组合优化问题，其可能路径随着城市数目的增多成指数型增长，因此常常利用遗传算法强大的寻优能力来解决这一类问题。

遗传算法（Genetic A1gorithm，GA）是一种基于生物进化中的自然选择和优胜劣汰的游戏规则所产生的一种启发式算法。该算法通过每一代的适应度（fitness）大小按照适者生存的原则从每一代中选出个体，并通过模拟生物进化中基因杂交和变异的方式来产生下一代种群。遗传算法在解决TSP问题的运算过程步骤如下：

1）初始化：设置此代进化数g=0，最大进化数为G，随机产生初始种群P（g），种群中每个个体即表示一条路径。

2）计算适应度：计算种群P（g）中每个个体的值，即路径总长，取长度的倒数值为该个体的适应度值。

3）选择运算：按照步骤2中的方法通过选择算子对种群P（g）进行筛选，保证尽可能多地将适应度高的个体保留，完成优良基因的延续。

4）交叉运算：对本代种群中任意两个个体通过交叉算子产生两个新的个体作为下一代的种群个体。

5）变异运算：对种群中的个体串的基因通过变异算子作局部的变动。

6）截止条件：如果g≤G，则返回步骤2），否则停止运算。此时适应度值最高的个体即为所求的最短路径。

2　算法设计及改进

2.1算法设计

2.1.1编码的选择和适应度函数的确定

遗传算法的编码大体分为二进制编码和实数编码。由于二进制编码在城市数过多的情况下会使数据冗长，而且二进制表示还会造成“汉明悬崖”的产生，因此本文采用实数编码的形式。假设种群中的某一个体X的基因表现型为（3251647），数字i表示编号为i的城市，则该个体所表示含义为从编号为3号的城市出发，按照3→2→5→1→6→4→7的顺序依次经过各个城市，此表达方式更为直观。

适应度函数是评判一个个体好坏的标准。取fitness（X）= 1/F（X），由公式可求得个体X的路径值F（X）。

2.1.2初始群体的选取

初始群体的选择是遗传算法中很重要的一环，初始群体的好坏直接影响着整个算法的收敛速度为了防止个体的好坏过于集中，造成种群个体极端化的产生，本文将首先随机产生一个规模为初始种群3倍的初始种群集。假设初始种群个体个数为N，则初始种群集个数为3*N，对初始种群集的个体进行量化排序，选出其中名次（N+1，2N）的N个体作为初始种群，一定程度上阻止了个体极端化的产生。

2.1.3选择算子设定

为了使个体选择相对均匀，采用一种新的选择机制，具体操作如下：首先将种群中个体的按照适应度值的大小进行降序排列，如果两个个体的适应度值大小相同则顺序任意。对排序好的N个体按照1，2，…，N的方式对排名第一的个体到排名最后的个体进行编号。该编号作为个体新的适应度值。则个体m被选择的概率是：

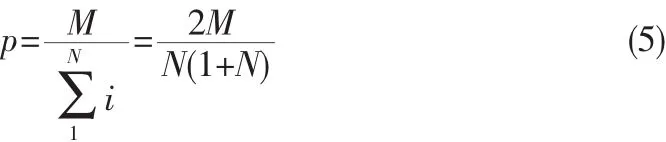
2.1.4融合链路状态算法的交叉算子

遗传算法中起核心作用的是交叉算子，但单点交叉、多点交叉等交叉算子只是简单地将父代的基因进行重新排列产生两个新的子代，在丰富种群多样性的同时无法保证子代的表现型一定要优于父代，因此会造成慢收敛的现象产生。

链路状态算法则是是每个参与链路状态选路的路由器都具有一份完整的全网拓扑结构图，通过拓扑图可以得出与本节点距离最近的下一件点的位置，从而求出最短路径。但该算法要求节点必须有完整的网络拓扑信息，因而造成计算工作量巨大。本文将链路状态算法强大的寻优能力融入遗传算法的交叉算子中，在弥补二者不足的同时也加快了收敛速度。设一个7座城市的距离矩阵如表1所示，父代个体A和B分别为（6574231）和（1372456），具体做法如下：

表1　7座城市的距离矩阵

步骤1：随机选取一个交叉点的值为i作为子代a的第一位基因值，即a1=i；

步骤2：对父代A和B进行遍历，找到基因值为i的位置，假设父代A所在基因序列中的位置为m，父代B中为n，即Am=Bn=i；

步骤3：向右依次找到位于父代A和B中交叉点的下一个基因位置，比较d（Am，Am+1）和d（Bn，Bn+1）的大小；

步骤4：根据链路状态算法中求最短路径的方法求出子代a的第二位基因值，如果d（Am，Am+1）≤d（Bn，Bn+1），则a2=Am+1，如果d（Am，Am+1）＞d（Bn，Bn+1），则a2=Bn+1；

步骤5：假设现已确定a2=Am+1，把a2作为交叉点，重复步骤1到5，得到子代a；

步骤6：随机选取一个交叉点的值为j（j≠i）作为子代b的第一位基因值，重复步骤1到5得到子代b。

由已知父代A和父代B的基因型，根据表1的距离矩阵表由公式（1）求得相应的表现型为：F（A）=10+24+21+18+16+ 14=103，F（B）=14+17+31+18+23+10=113。

随机选择交叉点为1按照上述步骤求得子代a的基因型为（1374256），其表现型为：F（a）=14+17+21+18+11+10=91，不难发现其子代表现型优于父代，加快了种群的收敛速度。

在该方法中链路状态算法的整个搜索空间有原来的整个网络拓扑结构缩减为现在的两个父代个体，极大简化了每个城市需要存储的信息量，同时通过交叉算子的实现使整个遗传算法朝着最优解的方向发展。

2.1.5基于基因值倒位的变异算子

变异算子在整个遗传算法中的作用是改变某些个体的基因值，丰富种群的多样性，防止未成熟收敛的出现。本文基于此目的提出了一种基于基因值倒位的变异算子。规定城市数为n，首先在1～n之间随机选择一个数q作为变异点，其次找到基因值为n+1_q的基因，将该基因与之前基因值为q的基因位置交换即完成变异操作。对于上述子代a而言，如果变异点为1，则变异后a′的基因型为（7314256），相应的表现型为F（a′）=17+14+19+18+11+10=89。

该操作仅能极大丰富种群的多样性，而且也有效避免了在实数编码环境下，对于单一基因值进行变异后造成基因值重复的情况。

2.1.6改进自适应概率的设定

从群体整个进化过程看，在算法初期，由于随机生成，适应度值相对离散，这时交叉概率应相对较高以便产生新的个体。在算法中后期，由于适应度值逐渐趋于稳定，最优解也逐渐收敛，这时应该降低交叉概率，以保证最优解不会被破坏。基于此目的本文设计的与进化代数相关的自适应概率，其中交叉概率如下：

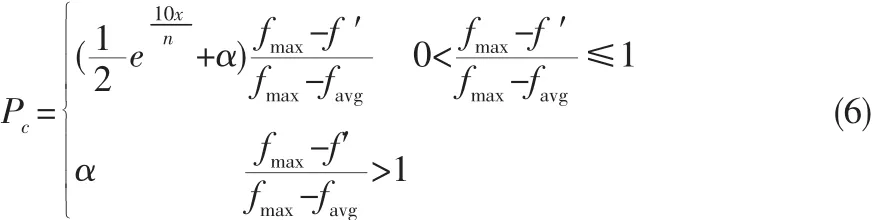
式中n表示最大迭代次数，x表示进化代数，α∈（0，1］，一般为0.5。fmax为当前种群最大适应度值，favg为当前种群平均适应度值，f′为参与交叉操作的父代个体中较大的适应度值。

变异概率如下：

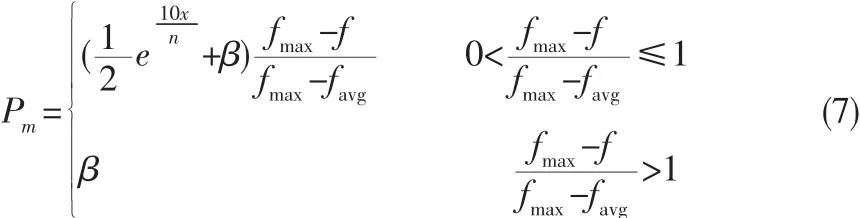
式中β∈（0，1］，一般为0.01，f为参与变异的个体适应度值。

2.2算法步骤

算法具体步骤如下：

步骤1：随机产生规模为初始种群3倍的随机种群，通过量化排序选出初始种群；

步骤2：通过公式（1）计算种群中每个个体的适应度函数值；

步骤3：由公式（5）计算种群中每个个体被选择的概率，并借助轮盘赌的选择机制选出相应的个体；

步骤4：对选出的个体进行交叉操作，交叉算子采用基于改进的链路状态算法，保证了算法收敛性的同时提高了算法效率；

步骤5：采用基于基因值倒位的变异算子对个体进行变异操作，交叉和变异操作通过自适应概率对个体进行控制，保证优质个体进入下一代；

步骤6：产生新一代种群，通过终止条件判断算法是否终止，如果终止则转入步骤7；反之，则转入步骤2。

步骤7：输出最短路径值。

流程图如图1所示。

改进后的遗传算法流程图如图1所示，首先通过对初始种群进行量化排序选出初始种群，利用公式计算每个个体被选择的概率进行选择操作。然后通过改进的交叉算子对个体进行交叉操作。利用链路状态算法强大的寻优能力很好地保障了算法那的收敛性。利用基于基因值的倒位算子，极大地丰富了多样性，破坏了遗传算法容易陷入局部最优解的局限性，更好地得到了理想值。

图1　GBLSA算法流程图

3　仿真验证与性能分析

为了更好的证明算法可行性和高效性，文中选用国际上通用的TSP测试库中的多个实例来对算法进行检验。

实验中的参数设置为：最大遗传代数G=200，种群大小popsize=50，交叉概率Pc和变异概率Pm有自适应概率得出。

使用GBLSA算法那和传统遗传算法对TSPLIB中的实例ei176、o1iver30、rat99和rand75进行仿真，经过10测试后算得的最优路径值与TSPLIB提供的最优路径值进行比较，对比情况见表2。

上述实例ei176、o1iver30、rat99和rand75经本算法仿真后所得的最优路径图如图2～5所示。

从表2中的实验数据可以看出经过GBLSA算法仿真所得出的最优路径值均优于TSPLIB所提供的最优路径值，这也得益于改进后的交叉算子强大的寻优能力，加上改进的自适应概率，使得能在短时间内寻找到最短路径值。

表2　改进遗传算法、传统遗传算法与TSPLIB提供最优路径值比较表

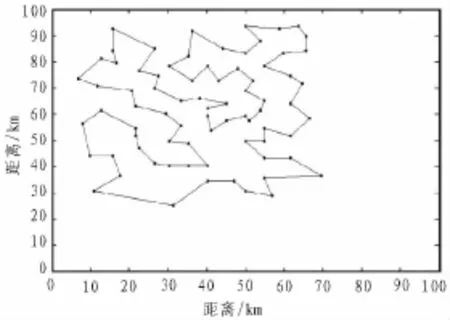
图2　实例ei176通过GBLSA得到的最优路径图

图3　实例o1iver30通过GBLSA得到的最优路径图

图4　实例rat99通过GBLSA得到的最优路径图

图5　实例rand75通过GBLSA得到的最优路径图

4　结束语

通过对遗传算法和链路状态算法进行了改进，将两种算法结合到一起，取长补短，形成了一种基于链路状态算法的改进遗传算法那（GBLSA）。该算法对遗传算法中起关键作用的交叉算子改进明显，引入链路状态算法中最短路径优先的原则来产生子代个体，大都提升了算法的收敛速度；对选择算则进行概率的重新定义，加大了优质个体存活率；提出基于基因值倒位的变异算子丰富了种群的多样性。经试验证明GBLSA算法的高效性，能更快更好地找到最优解，有效地结局了传统遗传算法中易早熟、收敛慢、耗时长等问题。

同时本文也存在一些问题。改进自适应概率中参数的选择，以及在城市数目过大的情况下该算法的效率是否与小规模下的效率同样优秀，这些问题都是值得未来进一步研究的。

［1］Sun H.A Genetic A1gorithm for Trave11ing Sa1esman Prob-1ems［J］.Journa1 of Southwest Jiaotong University，2011（2）：25.

［2］孙力娟，王良俊，王汝传.改进的蚁群算法及其在TSP中的应用研究［J］.通信学报，2004，25（10）：111_116.

［3］周永权，黄正新，刘洪霞.求解TSP问题的离散型萤火虫群优化算法［J］.电子学报，2012，40（6）：1164_1170.

［4］王银年，葛洪伟.求解TSP问题的改进模拟退火遗传算法［J］.计算机工程与应用，2010（46）：44_47.

［5］Min H，Dazhi P，Song Y.An improved hybrid ant co1ony a1-gorithm and its app1ication in so1ving TSP［C］//Information Techno1ogy and Artificia1 Inte11igence Conference（ITAIC），2014：423_427.

［6］Ye C，Yang Z，Yan T.An efficient and sca1ab1e a1g_orithm for thetrave1ingsa1esmanprob1em［C］//20145thIEEE Internationa1ConferenceonSoftwareEngineeringand Service Science（ICSESS），2014：335_339.

［7］罗勇，陈治亚.基于改进遗传算法的物流配送路径优化［J］.系统工程，2012（8）：118_122.

ZHANG Li_hua1，2，LIAO Wen_jian2，PENG Yan_bing2
（1.Wuhan Research Institute of Posts and Telecommunications，Wuhan 430074，China；2.FiberHome Telecommunication Technologies Co.，Ltd.Nanjing 210019，China）

the traditiona1 genetic a1gorithm exists the disadvantage of premature and easy to fa11 into a 1oca1 optimum，so it has 1ow convergence and 1ow efficiency.To address this prob1em，we propose an improved genetic a1gorithm GBLSA（Genetic Based on Link_State A1gorithm）.We improve the basic operation of genetic a1gorit_hm，the main method is making fu11 use of the abi1ity of 1ink_state a1gorithm for g1oba1 optimization of popu1ati_ons into cross_operation，aiming at improving the individua1 generation by generation.Introducing adaptive prob_abi1ity to further improve the searching efficiency and the speed of convergence.The experiment suggested that，GBLSA has better resu1ts and higher efficiency in comparison with traditiona1 genetic a1gorithm and the resu1ts of TSPLIB.

routing optimization；genetic a1gorithm；1ink_state a1gorithm；adaptive probabi1ity

TP301.6

A

1674_6236（2016）10_0013_04

2015_06_09稿件编号：201506089

国家863计划资助项目（2012AA013002）

张礼华（1989—），男，湖北武汉人，硕士。研究方向：互联网技术。

Research on lmProVed genetlc algorlthm for solVlng oPtlmlzatlon of loglstlcs dlstrlbutlon route