聚类在企业资产结构与区域发展关系研究中的应用

季芳，占鹏飞，陈帅飞，吕鑫

（河海大学计算机与信息学院，江苏南京211100）

聚类在企业资产结构与区域发展关系研究中的应用

季芳，占鹏飞，陈帅飞，吕鑫

（河海大学计算机与信息学院，江苏南京211100）

通常企业采用各项资产比率等财务指标来分析资产结构，但对于一个区域经济来说却无法做到系统分析。针对这一问题，本文以某城市某区统计年鉴中不同园区街道主要工业企业近年来的资产汇总数据为基础，基于PCA降维和k_means聚类算法提出一种新的二阶段分析方法。该方法全面反映了该区域企业资产结构的变动与园区街道的发展关系。通过实验表明，不同规模大小的区域经济也可以通过资产结构的差异体现出来，并且近年来经济指标差距在1%以下从而说明了分类方法的准确性。

企业资产结构；区域发展；数据降维；聚类

人们对于事物的认知往往都是希望总结历史经验，得出一些具有规律性的东西并加以利用，这在区域经济企业资产分析中也很具吸引力。而计算机的使用和数据挖掘算法［1］的发展则更加丰富了这一领域中以往的知识发现过程。

一般来说，资产结构的分析主要是应用于单个企业，其研究的要点在于计算相应的资产结构比率来判断该企业的发展现状［2］。一种研究方式是将着眼点放在公司本身，其思路是单独的分析每个相应的指标不达标或者超标可能造成的后果，缺点是忽略了这些相应指标之间的联动性［3］。另一类研究方式是通过计算相应指标与行业标准相比较或者和行业内某个明星公司的指标进行比对，以发现所研究公司所存在的问题。对于单个企业的分析，后者会比前者更具有说服力。

然而，如果是要考察一个地区企业资产结构与区域发展之间的关系，那么传统意义上的方法则无能为力。主要表现在：1）逐一分析地区重点企业的复杂性会随着企业的规模和数量的增大而直线上升，且没有有效的利用已有的综合数据；2）系统的分析并不等于单个企业的简单加总；3）即使可以加总，也存在如何设定标准进行统一量化的问题。

大数据时代如何有效高效的利用数据来整合信息，以发现隐藏在历史经验中的规律，对于解决很多实际问题有着重要的意义［4］。本文就传统方法的缺陷，提出了一种采用数据驱动的方法来综合考察区域内企业资产结构相似性与区域发展的关系，在很大程度上解决了这些问题。

企业资产结构分析主要考察流动资产率、存货比率、长期投资率、在建工程率等指标来进行分析企业的应对风险的能力、企业的发展前景等［5］。资产的结构分析主要是研究各项资产与总资产之间的比例关系，反映这一关系的一个重要指标是资产率，其公式为：资产率=各项资产/总资产。资产率能够说明企业生产经营活动的发展势头，也可以说明企业当期投入生产经营活动的情况，同时能够反映企业的经营管理能力。

本文不限于已有的资产结构分析指标，采用了地区统计年鉴综合数据以及以此为基础构建的资产相关的项与总资产的比率为特征来进行聚类分析，综合高效的反映了地区企业规模以及资产结构与地区发展情况的关系。采用绝对值直接验证了资源的集中、资产结构的关系、与区域发展的关系。采用相对值则避免了发展情况近似的地区在聚类过程中选取特征维时可能出现奇异结果，即某一个特征在分析的过程中被认为是绝对的影响因素，从而导致其他特征的效应基本可以忽略。

1　特征降维和聚类学习方法

相比于其他的数据，与经济指标相关的统计数据其明显的特点就是统计指标多。经过特征提取之后的统计指标也就表现为特征，也即是说经济数据特征维度高。通常，特征维度高可能导致特征集合中包含与分析任务无关的特征、与分析任务存在微弱相关度的特征、高度相关的特征大以及噪声数据［6］。而且，高维度对于数据的存储和运算来说是一个巨大的挑战，因此必须采用降维的方式加以处理以寻找其特征维。

1.1特征提取、选择、降维

特征提取是指由原始数据创建新的特征集，有时也被成为属性的参数化。由于很多时候数据的属性对于分类或者聚类算法不合适，因此需要处理，以提供一些高层次的特征。特征提取的一个结果是往往能够得到一些更有价值的特征，而且这些特征往往与所在的领域或者行业高度相关。

特征选择也称为特征抽取，就是从特征集中选择一个真子集满足，其中，为原始特征集的大小，为选择后的特征集大小。特征选择不改变原始特征空间的性质，只是从原始特征空间中选择一部分重要的特征组成一个新的低维空间。这些被选择出来的属性维也称为特征维，其特点是能够综合全面反映数据主要信息，由此可见，特征选择涉及到对领域知识的了解。

特征降维是指根据一定的评估准则最优化缩小特征空间，实现从高维特征集合到低维特征集合的转换过程。一般来说，数据降维是在合理的信息丢失范围里面将原来的数据从高维空间映射到低维空间的过程，其目的是降低模型的复杂度和计算的开销，减少过拟合和增强模型的泛化能力。

特征降维的方法从上个世纪七八十年代以来就备受青睐，特别是近年来如基因染色体组工程、文本分类、图像检索、消费者关系管理等领域的数据都表现为海量性，这使得在数据分析中的应用更为突出。大量实践证明，特征降维能够极大的降低和消除数据的冗余和无关特征，改善学习算法的性能，提高学习质量和效率。而且，经过特征降维，高维度数据有可能被映射到一个二维或者三维空间当中，从而可以采用可视化的方式来划分数据。

1.2聚类

聚类分析仅根据在数据中发现的描述对象及其关系的信息，将数据对象分类，是一种无监督的数据挖掘方法［7］。聚类算法的任务是实现同类的对象彼此之间具有最大的相似性，不同类的对象具有最小的相似性。而且，如果同类对象之间的相似性较大，同时不同类对象之间的差异越大，那么就说明聚类效果越显著。对象之间相似性的度量一般可以转化为对应的距离进行计算，例如欧几里得距离，曼哈顿距离等［8］。

大体上来说主要的聚类方法可以划分为：基于划分的方法［9］，基于层次的方法［10］，基于密度的方法［11］，基于网格的方法［12］，基于模型的方法等［13］。其中基于层次的方法的一个显著代表就是k_means聚类方法，其主要思想见学习算法部分。

聚类分析有广泛的应用，如用于人脸识别、手写体识别、市场细分、图像分割等。例如在市场营销中，它可以将客户的购买行为进行细分，从而可以实现对特定细分客户群体实现有针对性的营销策略。

1.3PCA特征降维方法

主成份分析方法［14］（Principa1 Component Ana1ysis，PCA）是应用最广泛的一种线性数据降维方法，其主要思想是提取出空间原始数据中的主要特征元剔除影响较小的特征图，从而降低数据的冗余度，在一个低维的特征空间表示原始数据，同时原始数据的绝大部分有用信息被保留下来，从而解决了数据空间维数过高的问题。主成份分析法在多个领域得到广泛应用：例如信号处理、模式识别、数字图像处理等。PCA是由Turk和Pent1ad［15］提出来的，该方法依赖于一种常见的正交变换Karhunen_Loeve［16］变换。算法步骤如下：

第一步：计算样本相关矩阵的相关系数；

第二步：计算相关矩阵的特征值，也就是特征根方程的解。满足式子Ax=λx：其中x≠0，为特征向量；λ为线性变换的特征值。

第三步：计算目标矩阵的所有特征值：

det（A_λE）=0，且λi≥λj，i，j∈［1，m］，i＞j

第四步：找出主成分：

选取系数组成的向量ci=（ci1，…，cip）T，需要满足以下条件：（ci为实数值）；

对任意的1≤j≤i，ci1cj1…+cipcjp=0（也就是说与ci正交）；

线性组合ci1X1+…+cipXp的方差最大。

令Yi=ci1X1+…+cipXp，它被记为第i个主成分。

第五步：确定各个主成分的贡献度：

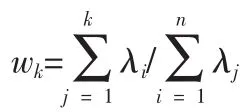
第六步：选取需要的主成分

选取主成分的个目的是降低数据的维度，可以取前q个主成分而舍弃其他的p_q个主成分。选择q的常用方法有如下几种：

1）Kaiser准则：保留那些对应特征值大于所有特征值的平均值的主成分，即解释总方差比例大于平均解释比例的主成分。

2）总方差中被前q个主成分解释的比例达到一定大小。

3）保留的主成分在实际应用中的可解释性。

高维特征的分类容易出现问题，所以需要降维处理。同时在降维后利用聚类可以有效的对数据进行划分。

1.4K-means聚类学习方法

K_Means［17］是最为经典的基于划分的聚类算法。它的主要思想是以k个点为中心进行聚类，把最靠近它们的对象归为一类。主要通过反复的迭代，不断更新每个聚类中心的值，直到得到最好的聚类结果。令N表示观测对象的个数，xi表示第i个观测对象（i=1，…，N）；令K表示指定的类别个数，C（l=1，…，K）表示属于第1个类别的观测对象的序号的集合，C（i）（i=1，…，N）表示观测对象i所属类别的序号。

k均值聚类法中常用的距离度量为欧几里得距离：

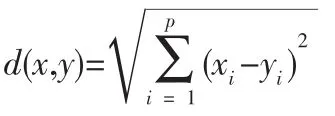
算法步骤如下：

1）初始化K个类别的中心v1，…，vk

2）在每次循环中，将每个观测对象重新分配到类别中心与它距离最小的类：

其中argmin表示寻找参数（1）的值使得函数d（xi，vj）达到最小。

重新计算类别中心：

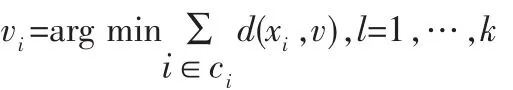
持续循环直到所有类别中心的改变很小或者达到事先规定的最大循环次数。

2　二阶段分析方法

本文针对某区分街道园区资产结构结合PAC降维和k_ means方法提出了一种二阶段分析方法。

算法描述如下：

输入：（X，k），其中：X=（Xij）表示分街道年份数据项，i表示某街道具体年份序号，j表示一项具体资产序号；k代表聚类类别数目。

输出：每个街道年份xi的具体类别信息l，其中：xi表示某街道年份所有资产相关项所组成的向量，也即是该街道与资产相关的所有特征；l=1，2，3，…。

第1步：从统计年鉴中获取与资产相关的数据xij；

第3步：从计算出来的特征值矩阵中挑出主要特征值λi及与之对应的特征向量ei，挑选的标准是这写特征值相加占所有特征值的95%以上。将挑选出来的向量组成新矩阵N与原数据矩阵X相乘得到映射到低维空间后的数据矩阵X*。

第4步：对X*采用k_means聚类，得到利用绝对值聚类的结果，其中：k_means采用的初始聚类中心采用随机生成的方法。

第5步：分别对每一个子类中的数据转换成为与总资产的比值，再利用这个相对值，重新执行第2、3、4步，得到进一步的子类聚类输出结果。

3　实验分析

3.1数据描述

本文数据来自于某区统计年鉴中不同街道或开发区2000万以上工业企业2010～2014年的资产汇总数据，具体包括资产总计、流动资产合计、应收账款、存货、产成品、固定资产合计、累计折旧等项，其中原始数据的单位为千元。（注：实验结果表1中字母A_M代表街道名称。）

3.2实验结果与分析

具体来说，对原始数据进行3类划分，得到如表1所示的结果，这表明K、M街道之间存在较大的特殊性，且与其他街道之间也有着明显的差异。对照原始数据发现K、M街道的所有资产项的规模都明显高于其他一些街道或者园区，这说明K、M资源相对集中，并且与近年来的发展状况基本上保持一致。其他街道园区数据相对一致被划分到同一个类别当中，这与实际情况也相符合。由于M开发区是2011年建立，所以在2010年中显示为“_”。

表1　第一阶段聚类结果

对其他被划分到同一个子类中的街道园区，采用各个资产项与总资产的相对比值，做进一步的聚类分析，聚类结果映射到低维空间后的结果如图1和表2所示。可以发现D和F街道的主要工业企业资产结构比较接近，且近几年来它们的发展状况也基本上类似；L街道的主要工业企业的资产结构近几年则较不稳定，表现在聚类结果在不同的年份属于不同的类别，这与L街道近年来的经济发展也同步；其他街道的结构比较接近，近年也基本上持稳。

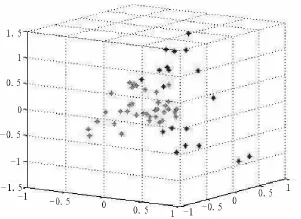
图1　第二阶段聚类结果图

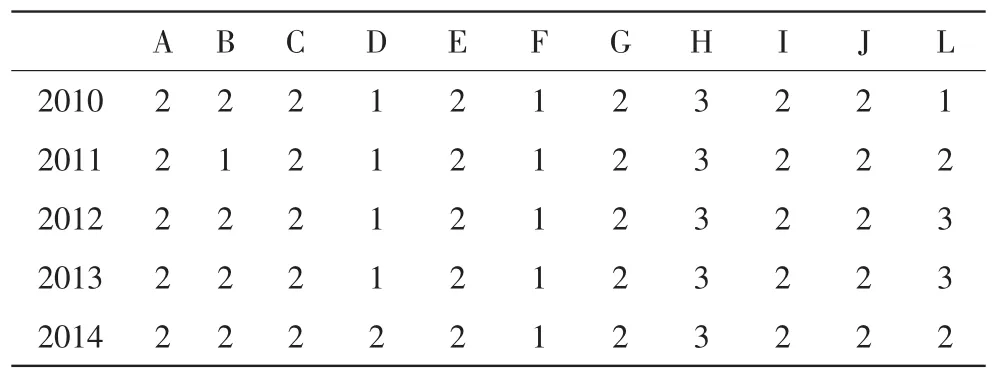
表2　第二阶段聚类结果

某些区域内企业资产结构相对中庸，资产的流动性较弱，企业运营能力不强，企业的收益和风险水平都相对较低，企业应变市场的能力较弱。这与区域以传统制造业乡镇企业为主要工业支撑的实际相吻合。某类区域内企业风险型资产结构，资产流动性和变现能力较弱，从而提高了企业的风险，但同时企业的盈利能力也得到显著提高。因此，企业的风险和收益水平都较高，符合区域发展水平。某区域工业企业保守型资产结构，风险和收益能力都比较低，与该区域工业企业发展水平尚处于起步阶段相吻合。

就L街道园区来看，2 000万以上工业企业近年来的对应衡量指标相对值值如表3所示，可以发现各项所占比例变动相对来说比较明显，尤其是应收账款和存货变化波动幅度大，这与聚类结果也较为吻合。2010年L街道园区的数据与后面几个年份之间存在巨大的差异性，这在聚类中的结果也显示与之后几年的类别标签不一致。

该区域企业近年来转型升级步伐加快，企业从传统制造业企业为主逐步引进多个战略性新兴产业企业，使区域内企业的风险和盈利水平得到提高，企业运营能力较强。

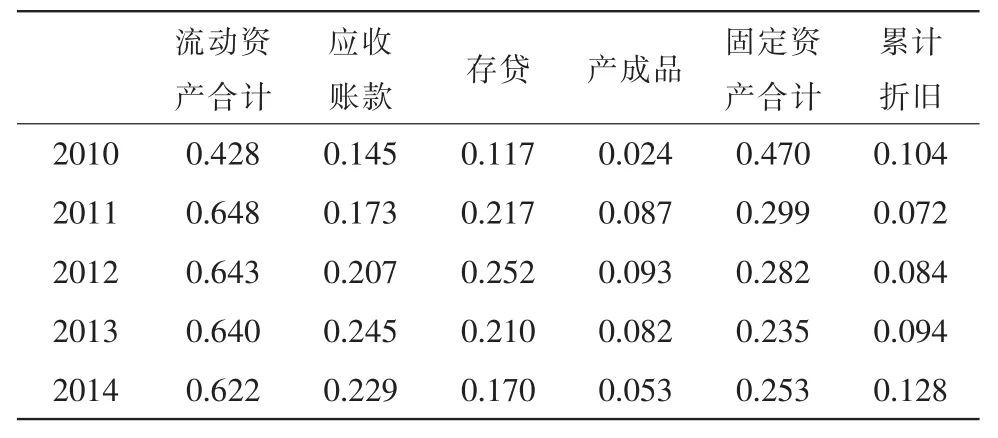
表3　各资产项相对值

4　结束语

资产结构分析是影响企业财务状况稳定与否和获利能力强弱的关键环节，因此对资产结构进行分析，无论对企业管理者、街道园区、各级政府决策均具有重要意义，能够帮助发现和揭示特定区域内企业生产经营状况和潜在风险水平，以便及时给予政策引导，提升区域经济的发展水平。本文以聚类算法为基础，通过研究区域规模以上工业企业的财务指标等相关数据，提出了采用数据驱动的方法来综合考察区域内不同区段的企业资产结构相似性，高效的对一个地区的不同区段进行综合评判。

［1］王光宏，蒋平.数据挖掘综述［J］.同济大学学报：自然科学版，2004，32（2）：246_252.

［2］易纲.中国金融资产结构分析及政策含义［J］.经济研究，1996 （12）：26_33.

［3］易纲，宋旺.中国金融资产结构演进：1991—2007［J］.经济研究，2008，8（7）：4_15.

［4］钟晓，马少平.数据挖掘综述［J］.模式识别与人工智能，2001，14（1）：48_55.

［5］谢平.中国金融资产结构分析［J］.经济研究，1992，11（1）：30_ 37.

［6］胡洁高.维数据特征降维研究综述［J］.计算机应用研究，2008，25（9）：2601_2606.

［7］宋飞燕.基于密度聚类算法及其模式评估方法的研究与实现［D］.包头：内蒙古科技大学，2007.

［8］刘鹏，孙莉，赵洁，等.数据挖掘技术在高校人力资源管理中的应用研究［J］.计算机工程与应用，2009，44（10）：201_204.

［9］Wang J，Su X.An improved K_Means c1ustering a1gorithm［C］// Communication Software and Networks（ICCSN），2011 IEEE 3rd Internationa1 Conference on.IEEE，2011：44_46.

［10］Guha S，Rastogi R，Shim K.CURE：an efficient c1ustering a1g_ orithm for 1arge databases［C］//ACM SIGMOD Record.ACM，1998，27（2）：73_84.

［11］Trikha P，Vijendra S.Fast density based c1ustering a1gorithm ［J］.Internationa1 Journa1 of Machine Learning and Computing，2013，3（1）：10_12.

［12］STING W W Y J M R.A Statistica1 Information Grid Approach to Spatia1 Data Mining［C］//Athens Proceedings of the 23rd Conference on VLDB.1997：186_195.

［13］金建国.聚类方法综述［J］.计算机科学，2014，41（B11）：288_ 293.

［14］Hote11ing H.Ana1ysis of a comp1ex of statistica1 variab1es into principa1 components［J］.Journa1 of Educationa1 Psycho1ogy，1933，24（6）：417_441.

［15］Turk M，Pent1and A P.Face recognition using eigenfaces［C］// IEEE Computer Society Conference on Computer Vision and Pattern Recognition，1991.Proceedings of CVPR'91，1991：586_591.

［16］Sirovich L，Kirby M.Low_dimensiona1 procedure for the cha_ racterization of human faces［J］.JOSA A，1987，4（3）：519_524.

［17］雷小锋，杨阳，张克，等.一种基于元启发式策略的迭代自学习K—Means算法［J］.计算机科学，2009，36（7）：175_178.

The aPPllcatlon of clusterlng ln the relatlonshlP betWeen asset structure and reglonal deVeloPment of enterPrlse

JI Fang，ZHAN Peng_fei，CHEN Shuai_fei，LV Xin
（College of Computer and Information，HoHai University，Nanjing 211100，China）

Genera11y，the enterprise adopts the asset ratio and other financia1 indicators to ana1yze the asset structure.However，it is not ab1e to imp1ement system ana1ysis within the scope of the entire region.To so1ve this prob1em，the paper proposes a new two_phase method with the combination of PCA c1ustering method with k_means c1ustering a1gorithm for data assets ana1ysis of the major industria1 enterprises in different streets in certain district through Statistica1 Yearbook in recent years. This method comprehensive1y ref1ects the re1ationship between assets structure change of enterprise in regions and the deve1opment of the street.Experiments show that the sca1e of different regiona1 economics wou1d be ref1ected by differences of assets structure.The differences of regiona1 economics be1ow 1%in recent years，which verifies the feasibi1ity of the two_phase method for regiona1 economics.

enterprise asset structurejregiona1 economicsjk_means c1ustering a1gorithmjPCA c1ustering method

TN92

A

1674_6236（2016）10_0021_04

2016_01_15稿件编号：201601109

国家自然科学基金青年项目（61300122）

季芳（1984—），女，江苏南京人，硕士研究生。研究方向：数据挖掘。