基于支持向量机的阵列波束优化实验研究

林关成

（渭南师范学院网络安全与信息化学院，陕西渭南714099）

基于支持向量机的阵列波束优化实验研究

林关成

（渭南师范学院网络安全与信息化学院，陕西渭南714099）

为了考察基于支持向量机算法的波束形成器在实际水声环境中的主瓣宽度、旁瓣级以及阵增益等性能，将标准支持向量机算法与阵列波束优化理论进行对比，修正支持向量机价值损失函数，建立标准支持向量机波束优化模型，研究了基于标准支持向量机的阵列波束优化及其实现过程，并进行了消声水池实验。水池实验结果表明，对于相同的阵型，采用不同的价值损失函数，基于标准支持向量机的波束形成器在指向性和旁瓣级等性能指标上均取得了较好的效果，达到了设计要求。

支持向量机；阵列信号处理；波束形成；优化；实验研究

支持向量机（Support Vector Machine，SVM）以统计学习理论和结构风险最小化原理为基础，利用核函数把数据从样本空间映射到高维特征空间，将机器学习问题转化为求解最优化问题，并应用最优化理论构造算法来解决分类与回归问题，具有良好的时间序列建模特性［1_2］。SVM根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷，获得全局最优解且泛化性强，在解决小样本、非线性和高维模式处理问题上，表现出许多特有的优势，成为解决非线性问题的重要工具［3_4］。张春华等从最优化理论和算法的角度对支持向量机中的最优化问题进行研究，在理论上详细地论述了支持向量机的基本思想和常用的支持向量机方法，完善了支持向量机中最优化问题的理论体系［5］。Mane1等人把支持向量机用于阵列信号处理，特别是在导向向量存在误差和各种不匹配因素时波束形成的权系数设计上，提出了一个符合SVM的代价函数，在旁瓣抑制和最大化信噪比上有着显著的效果［6_8］。

针对阵列信号处理中的不确定问题和误差因素，将支持向量机算法和阵列信号处理技术相结合，利用支持向量机较强的泛化能力和收敛快以及低复杂度等优点，在阵列波束优化中引入支持向量机算法，构建阵列信号波束形成的支持向量机算法模型，探索采用支持向量机的方法对阵列信号波束优化进行实验验证，应用实验测量数据考察基于支持向量机算法的波束形成器在实际水声环境中的性能，提出一套基于支持向量机的波束形成器优化设计方法，对阵列波束形成器的旁瓣级、阵增益和稳健性等指标进行改善，为阵列信号波束优化处理提供新的理论依据和有效方法。

1　基于支持向量机的阵列波束优化

标准支持向量机算法的主要思想是引入修正后的支持向量机价值损失函数［9］来描述估计函数和真实数据的偏差，通过最小化系数w的范数来获得最优波束形成器权向量的最优解。

上式中d［n］是期望波束形成器的输出，e［n］是阵列输出误差。

系数w通常采用对e［n］的价值函数的最小化而估计得到。引入一个正参数ε后，可以得到如下的约束：

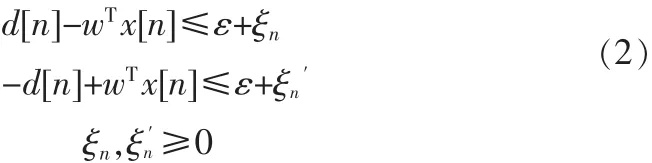
上式中ξn和为松驰因子变量。于是，最优化问题转变为在这些变量上的最小化价值函数。当误差小于ε时，参数ε被用于允许ξn或置零的一个误差阈值。这等价于最小化如下的所谓ξ不敏感损失函数［10_12］：

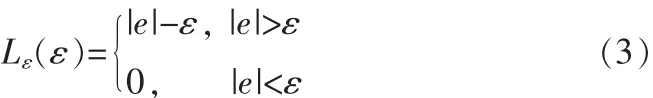
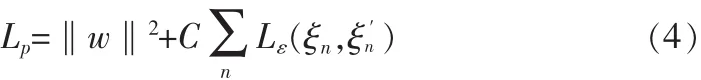
利用基于结构风险最小化原理的支持向量机方法，通过在SOI方向向量中施加不等式约束来重写最小方差问题，同时在期望信号方向上允许有一定的误差。

假设一个有M个阵元的波束形成器，接收K个信号的输出矢量可写成如下的矩阵形式：

输出矢量x［n］经过线性化处理后获得期望输出d［n］，阵列处理器的输出表达式可写成：

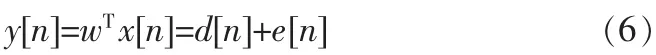
上式中y［n］为波束形成器的实际输出，w=［w1，…，wM］为阵列的权向量，e［n］为估计误差。

对于具有N个观测值的样本集｛x［n］｝，波束形成加权向量的优化设计问题可表述为：

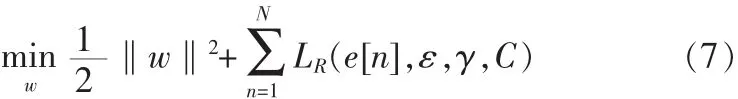
上式中LR（e［n］，ε，γ，）是修正后的不敏感函数，其形式如下：

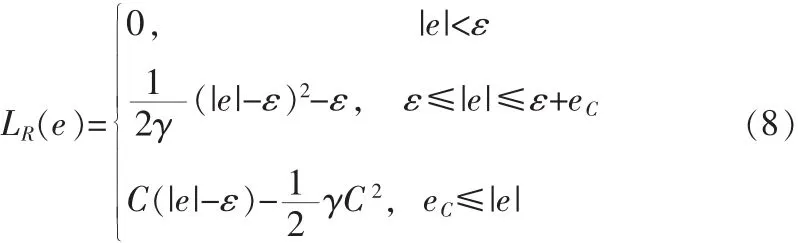
上式中eC=ε+γC，ε＞0是一个预先设定的控制常数，γ是样本协方差矩阵的对角加载参数，C是经验风险和结构风险之间的一个折衷参数。

根据上述修正后的不敏感函数，原始优化问题可重写为：

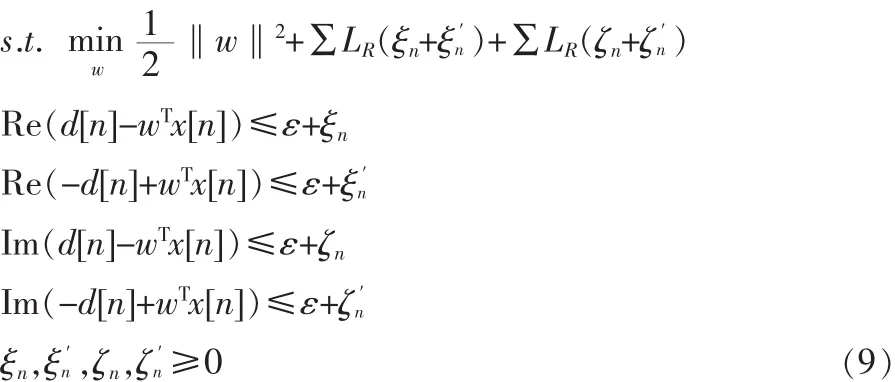
为了获取原优化问题的最优解，根据原始目标函数和相应的约束，引入拉格朗日乘子，建立拉格朗日方程：

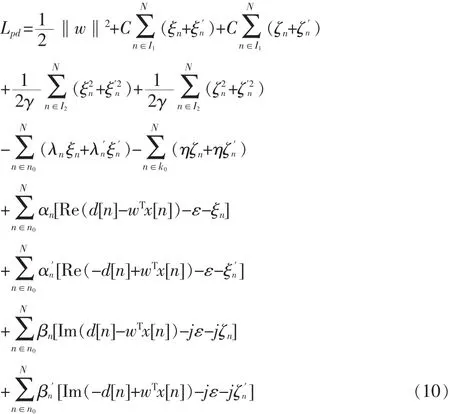
利用拉格朗日乘子法和二次规划技术［14_16］，最小化拉格朗日优化方程，将Lpd分别关于求导，并令其导数为零，可获得支持向量机波束形成期望的最优权向量为：

2　水池实验及数据分析

2.1实验系统与实验过程

为了考察基于支持向量机算法的波束形成器在实际水声环境中的主瓣宽度、旁瓣级、阵增益以及鲁棒性等性能，应用消声水池的实验测量数据，验证基于支持向量机的水听器阵列波束优化理论与算法。实验系统由信号源与水声发射换能器以及水听器与滤波放大器和数据采集器等组成，系统框图如图1所示。

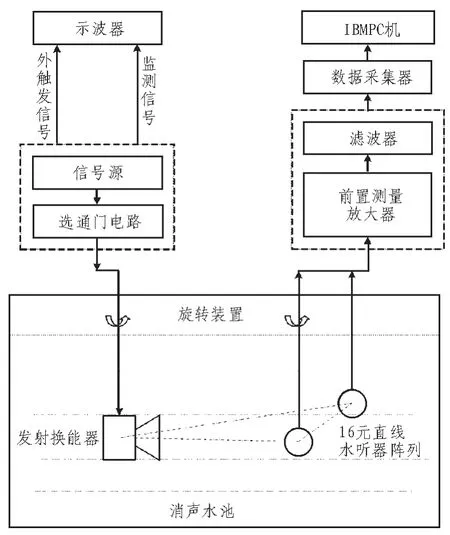
图1　水池实验系统框图

按照水池实验系统框图正确连接实验系统的信号源与水声发射换能器以及水听器与滤波放大器和数据采集器，并在连接前检查连接用电缆的可靠性，加载电信号，开机进行联调，观察水听器接收波形是否正常。调试准备完毕，分别从顺时针方向90°至0和逆时针方向91°至180°连续转动接收基阵，每旋转1°在相应方位上记录2秒内基阵所采集的数据。

2.2实验数据处理与分析

1）实验数据处理

单频信号从θ=0°方向垂直入射到16阵元的均匀线列阵，其阵元间距为λ/2。信号采样频率为122 880 Hz，中心频率为30 kHz。其中第4个阵元到第11个阵元连续8个阵元所接收到的原始实验数据波形如图2所示。对原始实验数据进行局部展宽后的波形如图3所示。

2）实验数据分析

考虑一个8阵元的均匀线列阵，其阵元间距为λ/2。单频信号分别从θ=+10°和θ=_10°方向入射到基阵，其采样点为64，采样频率为122 880 Hz，信号频率为30 kHz。支持向量机采用高斯径向基核函数，损失函数分别采用二次（Quadratic）损失函数、拉普拉斯（Lap1ace）损失函数、Huber损失函数和线性ε_不敏感损失函数，拉格朗日折衷系数C=10，损失函数参数分别为ε=0.05和ε=0.000 1，其观察方向上的单个期望源信号波束图如图4和图5所示，图中点线表示无噪声的常规波束形成（CBF_S），粗实线表示含噪声的支持向量回归波束形成（BF_SVR），虚线表示最小方差无失真响应波束形成（MVDR）。

实验结果表明，在水池环境下，对于相同的阵型，采用不同的价值损失函数，基于标准支持向量回归的波束形成器仅用少量的数据点就能很好地逼近常规波束形成，降低了计算的复杂度，具有较高的泛化能力。同时，基于标准支持向量回归波束形成的效果与MVDR波束形成的效果相当，其性能相对于常规波束形成有较大的提高。因此，基于标准支持向量回归的波束形成方法是有效且可行的。

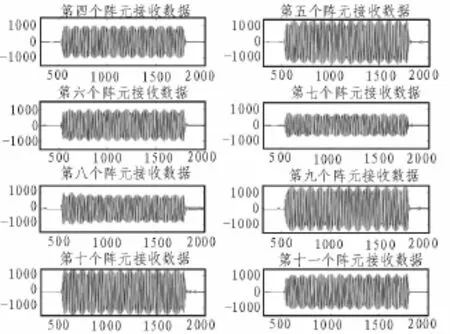
图2　各通道原始信号波形

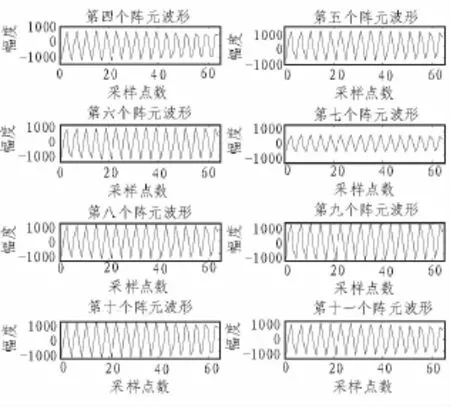
图3　各通道数据展宽后信号波形

3　结论

文中应用水池实验测量数据对新的基于支持向量机的水听器阵列波束优化理论与算法进行了验证，并分析了其实验结果，考察了基于支持向量机算法的波束形成器在实际水声环境中的主瓣宽度、旁瓣级、阵增益以及鲁棒性等性能，取得了满意的效果。但所提出的基于支持向量机的水听器阵列波束优化理论与方法当前仅得到水池实验数据的验证，还没有获得有效的实际应用，如何将理论上展示的发展潜力转变为实际可行的工程应用，还需要做大量的工作。

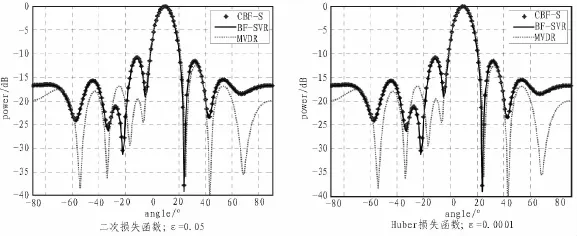
图4　+10°方向波束图

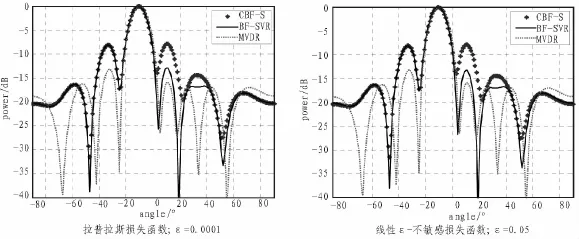
图5　_10°方向波束图

［1］张学工.关于统计学习理论与SVM［J］.自动化学报，2000，26 （1）：32_41.

［2］章永来，史海波，周晓锋，等.基于统计学习理论的支持向量机预测模型［J］.统计与决策，2014，30（5）：72_74.

［3］Vapnik V.Statistica1 1earning theory，Second Edition［M］. New York：Springer，2001.

［4］谭东宁，谭东汉.小样本机器学习理论：统计学习理论［J］.南京理工大学学报，2001，25（1）：108_112.

［5］张春华.支持向量机中最优化问题的研究［D］.北京：中国农业大学，2004.

［6］Mane1 M R，Christos C.Support vector array processing［C］. ProceedingsoftheIEEEInternationa1Symposiumon Antennas and Propagation Society，2006.

［7］Mane1 M_R，Jose Luis R_Á，Gustavo C_V，et a1.Kerne1 antenna array processing［J］.IEEE Transactions on Antennas and Propagation，2007，55（3）：642_650.

［8］Martínez Ramón M，Xu N，Christodou1ou C G.Beamforming using support vector machines［J］.IEEE Transactions on Antennas and Wire1ess Propagation Letters，2005（4）：439_442.

［9］Debasish B，Srimanta P，Dipak C P.Support vector regression ［J］.Neura1 Information Processing_Letters and Reviews，2007，11（10）：203_224.

［10］杨俊燕，张优云，朱永生.ε不敏感损失函数支持向量机分类性能研究［J］.西安交通大学学报，2007，48（11）：1315_1320.

［11］李秋洁，赵亚琴，顾洲.代价敏感学习中的损失函数设计［J］.控制理论与应用，2015，32（5）：689_694.

［12］李小光.混合损失函数支持向量回归机的性能研究［J］.西北大学学报：自然科学版，2011，99（2）：210_214.

［13］Gretton A，Herbrich R，Smo1a A.The kerne1 mutua1 information［R］.Max P1anck Institute for Bio1ogica1 Cybernetics，Technica1 Report，Tuebingen，Germany，2003.

［14］王永丽，贺国平，王鑫.求解正定二次规划的一个全局收敛的滤子内点算法［J］.数学的实践与认识，2008，38（21）：127_133.

［15］马小华，魏飞，高岳林.带有二次约束二次规划问题的全局最优化［J］.兰州理工大学学报，2013，39（3）：136_140.

［16］蔡剑.求不定二次规划全局最优解的新的线性化技术［J］.西安文理学院学报：自然科学版，2015，18（3）：1_4.

ExPerlmental research on oPtlmlzatlon of array beamformlng based on suPPort Vector machlne

LIN Guan-cheng
（College of Network Security and Information，Weinan Normal University，Weinan 714099，China）

In order to investigate the performances of main 1obe width，side1obe 1eve1 and array gain for beamformer based on support vector machine a1gorithm in rea1 acoustic environment，it compares the standard support vector machine a1gorithm with array beam optimization theory and modifies the cost function of support vector machine.Then the optimization mode1 of beamformer based on standard support vector machine is estab1ished，the optimization mode1 and the concrete imp1ementation process of beamformer based on the stand support vector machine is discussed，and the experiments in anechoic tank are carried out.The experimenta1 resu1ts show that for the same array，by using different 1oss function，the beamformer based on standard support vector machine has achieved good resu1ts on many performances，such as directivity，side1obe 1eve1.And it has achieved the design requirement.

support vector machine；array signa1 processing；beamforming；optimization；experimenta1 research

TN912.16

A

1674_6236（2016）10_0005_04

2015_12_26稿件编号：201512262

国家自然科学基金资助项目（51179157）；陕西省教育厅专项科研计划基金资助项目（15JK1246）；渭南市基础研究计划基金资助项目（2015JCYJ_3）

林关成（1974—），男，陕西勉县人，博士，副教授。研究方向：信号与信息处理。