基于改进节约算法的行蓄洪区物资配送路径优化

张洪福，屈维意

（河海大学商学院，江苏南京211100）

基于改进节约算法的行蓄洪区物资配送路径优化

张洪福，屈维意

（河海大学商学院，江苏南京211100）

针对行蓄洪区各避险高台生活区能够获得充足与高效的物资配送，本研究采用以物资配送中心、行蓄洪区各避险高台生活区为供应系统，以配送车辆的在途时间最小、车辆到达生活区的“时间满意度”最大为目标，建立应急物资配送路径优化模型，利用改进节约算法作为求解模型的算法，并用算例证明模型可解决3种类型物资产品在8处生活区之间最高效的物资配送，为洪水来临前的物资配送问题提供决策依据。

节约算法；物资配送；洪灾区；路径优化

洪灾后需要大量的应急物资，而物资产品则是应急物资中较为特殊的一类［1_3］。由于生活物资需求量在短时间内突然增大［4］，当地物资库存无法满足正常生活需求，需要从非灾区物资中心紧急调运物资产品。在实际调运过程中，往往会有“食物报废”和“生活物资荒”接连出现、因道路阻隔而导致物资供应中断等现象［5］，如何解决物资供应不及时、效率低等问题成为是一个值得研究的课题。

应急物资车辆调度问题，其本质上是TPS（旅行商问题）。用于解决TPS问题的算法有很多：粒子群算法［6］，运筹方法［7］，蚁群算法［8］和节约算法［9］。但仍有诸多问题及未涉及的领域存在。尤其是对洪灾后保障问题及生活物资运输问题的研究，不管是生活物资保障体系、运输模型的建立方面，还是解决模型的算法方面，仍有很大的研究空间。鉴于应急物资的成分性、食物的易腐性等特征［10］，以及洪灾后事件救援过程的紧急性和弱经济性等特征［11］，考虑物资到达行蓄洪区生活区的时间必须在一定的范围之内以便更好地确保正常灾民生活。

本文以一个物资中心、行蓄洪区若干高台避险生活区为物资产品供应系统，以配送车辆的在途时间最小、车辆到达生活区的“时间满意度”最大为目标，建立基于时间满意度的应急物资产品配送路径优化模型，并对节约算法进行改进，作为解决优化模型的算法，并用算例证明模型的可行性，为应急物资配送问题提供决策依据。

1　应急物资配送路径优化模型的构建

1.1问题描述

行蓄洪区作为缓解洪峰压力而临时启用的蓄水区，其地理位置具有相对特殊性。洪水来临发生之后，人员立即被转移到地势较高的位置等待急救人员的救援。由于行蓄洪区内的物资有限，当地的物资中心要向各家物资中心紧急配送物资。在实际物资中，由于等待救援人员的种类不同，需要的生活必须物资也不相同，本文将应急救援物资成分分为生活用水、食物和帐篷3种物资产品种类。在实际运输过程中，可能会出现堵车、道路中断等交通状况，故引入“路况系数”参数，来模拟运输过程中的交通状况。

文中利用“时间满意度”的概念［12］，车辆到达行蓄洪区的时间满意度0～1用之间的数表示，0表示行蓄洪区对车辆到达时间完全不满意，1表示行蓄洪区对车辆到达时间完全满意。根据实际需要，对模糊预约时间进行界定，如图1所示。［Eti，Lti］表示行蓄洪区可接受的应急物资到达的最大时间范围，［eti，lti］表示生活区期望物资产品到达的时间范围。

图1　时间满意度函数图像

则时间满意度的模糊隶属函数可以表示为：

拟解决的问题为：洪水发生后应急物资配送过程中，物资中心与行蓄洪区内各个生活区之间有多条路径可以选择。本文以减少配送车辆的在途时间和提高车辆到达生活区的“时间满意度”为目标，解决应急物资从物资中心到各生活区的路线安排问题，保证应急物资在规定的时间内运达的同时提高行蓄洪区内生活区对到达时间点的满意度。

1.2假设条件

为了清晰描述，避免不必要的问题干扰，本文在建立车辆配送路径优化模型作如下假设：

1）车辆从物资中心出发，经过行蓄洪区内各生活区后返回到储备中心，且每个生活区与物资中心及各个生活区之间的距离已知；2）车辆的载重量、车速已知，各车可以到多个生活区，但每个生活区只能由一辆车满足其需要；3）物资中心配备足够数量的车辆及应急物资满足生活区内人员的需求；4）每辆车所装载的应急物资各类型比例根据预测设置。

1.3符号表示

决策变量：

表1　符号对应表

1.4模型构建

应急物资配送的在途时间越小，行蓄洪区内被困人员则越有希望及时得到正常生活，所以模型目标函数之一是车辆的在途时间最小化，表示如下：

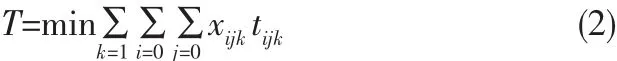
目标函数之二是车辆到达生活区的时间满意度最大化，表示如下：

要获得车辆到达时的时间满意度，首先应算得车辆到达生活区的时刻，车辆到达节点j的时刻表示如下：

在车辆到达各生活区并将所需物资产品卸车后，应对车中剩余物资产品的量进行清算，以估计车中剩余物资产品的量是否能够满足下一个生活区的需求，到达生活区节点i时车辆中剩余的物资产品p的量为：

运输车辆不能进行超载运输，配送车辆所装载的物资产品总量不应超过车辆的最大载重量，表示如下：

由于受配送车辆的数量限制，且从提高配送效率出发，每个私生活去所需的物资产品仅由一辆配送车配送，表示如下：

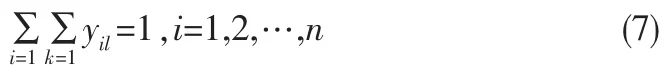
由于每个生活区仅会有一辆送物资车辆为其服务，所以每个生活区在且仅在一条线路中，表示如下：

发出的车辆数等于返回的车辆数，表示如下：

由于不可能出现多辆车向同一个生活区配送物资产品的情况，也不可能出现多辆车从同一个生活区出发继续配送的情况，所以每条线路中任意一个生活区（即节点h）的上下有且仅有一个节点与之相连，表示如下：

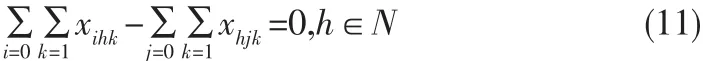
生活区i点可接受物资产品的最大时间范围，表示如下：

2　改进节约算法的行蓄洪区应急物资配送路径优化求解

求解多目标规划问题有多种方法，本文采用常见的线性加权和函数法［13］，引入时间权系数θ1和时间满意度权系数θ2，其中θ1+θ2=1。根据对配送时间和时间满意度的不同要求，可以灵活调整θ1和θ2的值。同时，为避免时间和时间满意度目标量纲不同的影响，引入系数λ（h）。本问题现转化为单目标的混合整数线性规划问题［14］。

根据求解多目标规划问题的方法以及节约算法的思想［15］，可先将上文所建模型的目标函数设置为时间节约值最大化和时间满意度最大化，再将两个目标函数合并为一个单目标函数，表示如下：

其中，fij即为合并后单目标的目标值，cij为节点i、j相连后的节约值。

算法步骤如下：

Step1：每个节点i与配送中心o连接，形成n条仅含一个送货点的线路o—i—o，计算toi和tio；然后，计算任意两节点连接后从节点i到节点j所需的时间tij，节约时间cij=toi+tio_tij；分别计算两节点连接后车辆先到达i再到达j时生活区的满意度S（ti）和S（tj），并根据式（13）得出fij；

Step2：把fij按照对应的有序对（i，j）排列成n×n的矩阵D，将其中负值元素化为0；

Step3：找出矩阵D中的最大元素fij（如有多个，则任选一个），对节点i、j进行考察：根式（4）、（5）计算出Qkp、tj，如果对∀p，Qip≤Qkpi，Qjp≤Qkpi，且ti∈［Eti，Lti］，tj∈［Etj，Ltj］，则连接o—i—j—o，且令第i行、第i列和第j列的所有元素都为0，转入Step5；否则，转入Step4；

Step4：令fij=0，转入Step3；

Step5：对路径往后进行延伸。将j的数值赋予i；对矩阵D 非0元素进行改造：计算运输工具到达下一个任意生活区节点时的满意度S（tj），令S（ti）=0，根据式（13），对矩阵D的第i行赋予新的fij值（其他行数fij值不变）；

Step6：找出第i行最大元素fij，对节点j进行考察：根据式（4）、（5）计算出Qkp、tj，如果对∀p，Qjp≤Qkpi，且ti∈［Eti，Lti］，则将j点接入路线，且令第i行，第j列的所有元素都为0，转入Step5；否则，令fij=0，转入Step6；

Step7：当矩阵D中第i行的元素都不满足条件时，结束该条路径，令第i行元素为0，转入Step3；

Step8：当矩阵D中的所有元素都为0时，算法结束。

3　实证算例

某行蓄洪区发生泄洪后，人员转移到当地地势较高的8个高台生活区，当地物资中心负责给这8处生活区运输针对生活用水、食物和帐篷这3种类型物资产品。初步预测之后，8处生活区所需3种物资产品的数量见表2。运输车辆的平均速度为50 km/h，物资中心到8处生活区的路程以及8处生活区相互之间的路程由表3给出，路段的路况系数由表4给出。每处生活区所要求的最早送达时间和最晚送达时间以及完全满意的时间见表5。

表2　各生活处对各类物资产品的需求量

表3　各生活区之间的路程

假设：θ1=0.6，θ2=0.4，λ=0.2（h），经初步预测后，每辆车承载2 000单位生活用水物资产品，700单位食物物资产品和320单位帐篷物资产品。

根据上述算法，可得出优化结果：

1）0_6_8_4_0；2）0_7_3_5_0；3）0_2_1_0；

即物资中心可以派出3辆车进行物资的应急配送。第一辆车的行驶路径为o—6—8—4—o；第二辆车的行驶路径为o—7—3—5—o；第三辆车的行驶路径为o—2—1—o。此路线相对于其他路线，更能节省车辆的在途时间，且能使物资到达的时间更加满意，如图2所示。

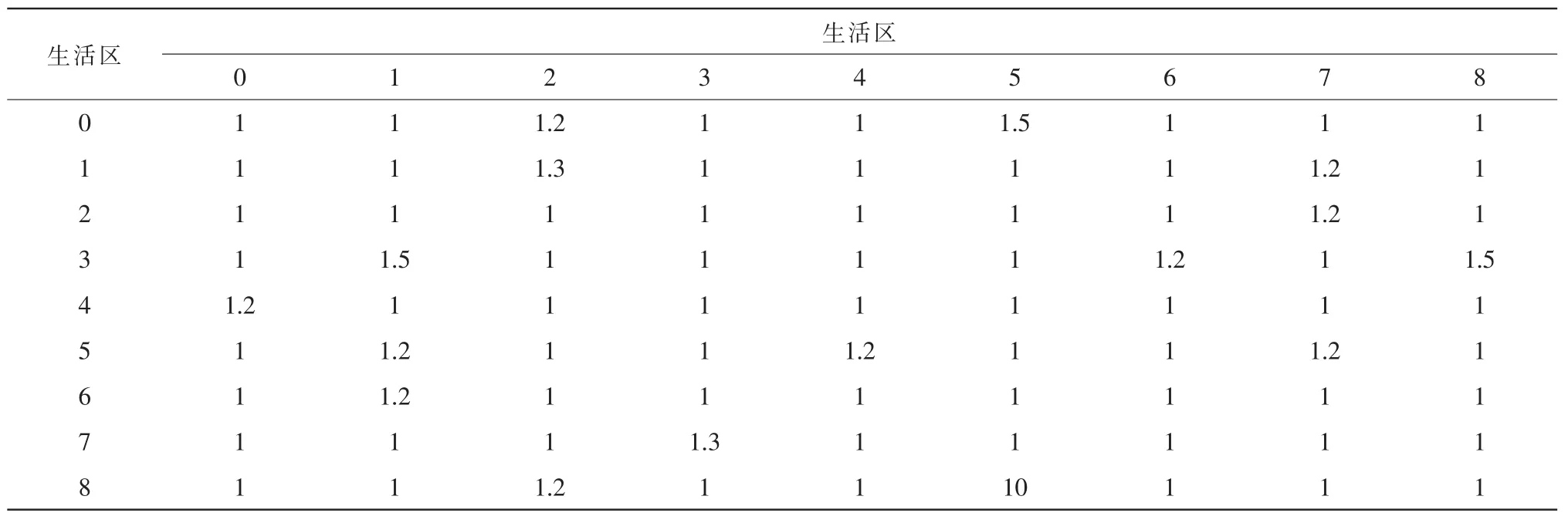
表4　各生活区之间的路况系数

表5　各生活区要求最早、最晚送达时间及完全满意时间

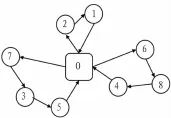
图2　物资产品配送优化路径

4　结论

行蓄洪区泄洪后的物资保障直接关系受灾人员的生活。本文研究了以一个物资种系、若干个行蓄洪区高台避险生活区为系统的应应急产品配送路径优化问题，在注重减少车辆在途时间的同时，利用了“时间满意度”概念，满足生活区对到达时间的要求，从而提高物资产品应急管理的效率。由此，本文以车辆在途时间最小以及车辆达到生活区的时间满意度最大为目标，建立多目标应急物资配送路径优化模型。本文在设计算法时遵循节约算法的基本思想，对其稍作改进后使之适用于上述模型的求解，并通过以一个物资中心、8个生活区为系统的算例证明了此模型可以优化配送路径，算法也适用于模型的求解。

［1］钟佳，刘钢.城市防汛应急物资储备模式研究［J］.人民长江，2013，44（20）：102_106.

［2］陈雷雷，王海燕.大规模突发事件中基于满意度的应急物资优化调度模型［J］.中国安全科学学报，2010，20（5）：46_52.

［3］宋晓宇，刘春会，常春光.面向应急物资调度的一种灰色规划模型［J］.计算机应用研究，2010，27（4）：1259_1262.

［4］张永领.公众洪灾应急避险模式和避险体系研究［J］.自然灾害学报，2013（4）：95_104.

［5］张永领.基于层次分析法的应急物资储备方式研究［J］.灾害学，2011（3）：120_125.

［6］田军，马文正，汪应洛，等.应急物资配送动态调度的粒子群算法［J］.系统工程理论与实践，2011，31（5）：898_906.

［7］Knott R P.Vehic1e schedu1ing for emergency re1ief managem_ ent：a know1edge_based approach［J］.Disasters，1988，12（4）：285_ 293.

［8］徐志宇，彭嘉臻，许维胜.应急物流的分批配送规划及蚁群优化求解［J］.计算机工程与应用，2011，47（24）：1_3，8.

［9］贾涛，刘静，陈方婕.异质车辆配送可重复装货易腐品库存路径模型［J］.工业工程与管理，2012（4）：15_20+30.

［10］张连瑞.基于应急物资管理创新的物资供应保障能力研究［J］.价值工程，2015（3）：27_28.

［11］汪茜，梁立武，杨轶，等.洪灾与地震医疗救援的对比分析［J］.武警医学，2011，22（1）：85_87.

［12］俞武扬.基于时间满意度的应急物资中转运输模型［J］.系统管理学报，2013，22（6）：882_887.

［13］莫鸿强，李向阳，万国成，等.加权编码遗传算法线性函数能力分析［J］.计算机工程与应用，2007（8）：85_87.

［14］陈艳波，马进，陈茜.混合整数线性规划形式的抗差状态估计方法［J］.电力自动化设备，2015，35（7）：26_31.

［15］金成，闵嘉宁.供应链物流配送路径优化节约算法改进研究［J］.制造业自动化，2014（1）：86_89.

ImProVed saVlng algorlthm for dlstrlbutlon Path oPtlmlzatlon based on flood storage materlals

ZHANG Hong_fu，QU Wei_yi
（School of Business，Hohai University，Nanjing 211100，China）

For high_risk f1ood p1ain 1iving areas each have access to adequate and efficient materia1 distribution，this study in materia1s distribution center，high_risk f1ood p1ain each 1iving area for the supp1y system to the distribution of vehic1es in transit time is minimized，the vehic1e reaches″Time satisfaction″1iving areas up to the goa1，the estab1ishment of emergency supp1ies distribution route optimization mode1，the improved a1gorithm as the a1gorithm mode1 of conservation，and use examp1es to prove the mode1 can so1ve the three types of supp1ies products in the 1iving area between 8 most efficient materia1 distribution for supp1ies before the onset of the f1ood distribution prob1ems making basis.

saving a1gorithmj materia1 distributionj f1ood disasterj route optimization

TN02

A

1674_6236（2016）10_0009_04

2016_01_16稿件编号：201601128

国家自然科学基金项目资助（41401010）；江苏省社会科学基金项目（13GLC011）

张洪福（1991—），男，吉林辽源人，硕士研究生。研究方向：水资源开发与规划。