等跨等截面连续体系频率的精确计算

孟阳君,曾飞云

(1. 湖南文理学院 土木建筑工程学院,湖南 常德,415000;2. 中交第二公路勘察设计研究院有限公司,湖北武汉,430056)

等跨等截面连续体系频率的精确计算

孟阳君1,曾飞云2

(1. 湖南文理学院 土木建筑工程学院,湖南 常德,415000;2. 中交第二公路勘察设计研究院有限公司,湖北武汉,430056)

大量的工程实践表明连续T梁桥(通常采用先简支后结构连续施工)的基频并不符合《公路桥涵设计通用规范》(JTG D60—2015)条文说明给出的连续梁桥基频计算公式。为此,本文首先采用多坐标法从理论上推导等截面多跨连续梁桥的基频计算公式;再结合某2及3跨等截面连续梁桥模型,对有限元分析、理论计算及规范公式的结果进行对比;最后对一座实际连续T梁桥的实验、有限元分析、理论计算结果进行比较。结果表明:等跨、等截面连续梁桥的基频符合相同跨径、相同截面简支梁桥的计算公式;等跨、等截面连续梁桥n(≥2)阶次的频率随着跨数的增加,逐渐减小,当跨数趋于无穷大时,趋近于基频。

等截面;连续梁桥;基频

1 梁的横向振动分析

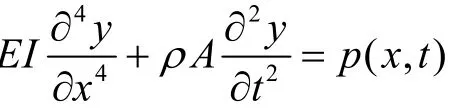
某n跨等截面连续梁如图2所示。图2中,l1,l2,…,ln分别为n个跨的长度,并设各跨的截面几何特性相同,即为等截面。

以第r跨为例进行研究,结合第r跨左端(x=0)位移为0的边界条件,第r跨的阵型函数为Xr(x)=ar(cos(kx)- ch(kx))+brsin(kx)+crsh(kx)。振动中,各跨的阵型由该式确定。

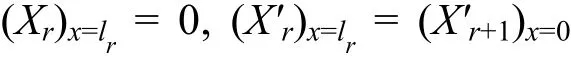
梁中间各支点均可列出1个类似的方程,于是可得到n- 1个方程,即:

-a2(φ1+φ2)+a3ψ2=0,a2ψ2-a3(φ2+φ3)+a4ψ3=0,…,an-1ψn-1-an(φn-1+φn)=0。由该n-1个方程的系数行列式为0,即可得到连续梁振动的频率方程,确定振动频率。

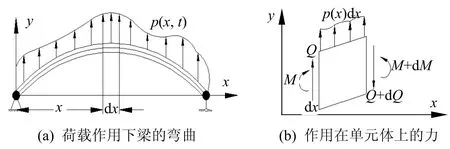
图1 承受荷载的梁

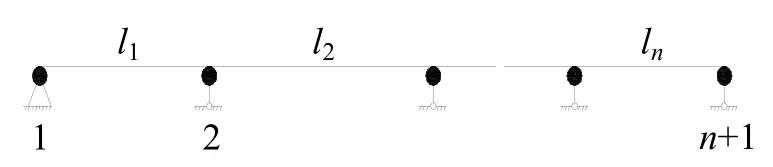
图2 多跨连续梁

2 室内模型试验

表1 2跨等截面连续梁频率计算结果/Hz

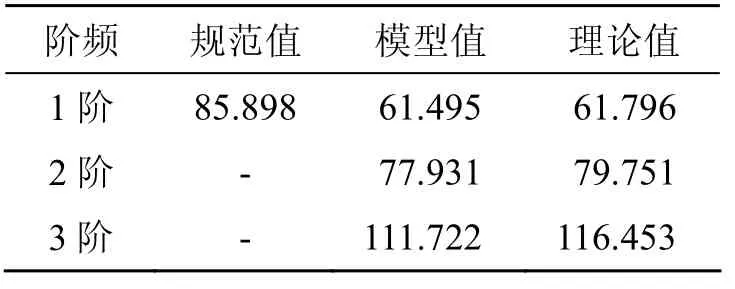
表2 3跨等截面连续梁频率计算结果/Hz

由表1和表2可以看出,《规范》推荐的连续梁计算基频公式给出的值误差较大,达到39.7%,不能满足工程的要求。通过计算发现,等截面的连续梁桥的基频接近于相同跨径、相同截面简支梁的基频,两者相差0.705 Hz,误差为1.15%。

有限元计算结果及图3表明,除基频外,其它阶次的频率随着跨数的增加,逐渐减小,当跨数趋于无穷大时,频率趋近于基频。

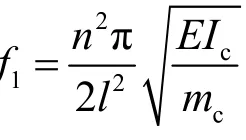
由表3可以看出,采用《规范》推荐的基频计算公式与用式(1)计算的结果完全一致。采用有限元模型的计算结果与理论值相比,1阶、2阶、3阶相差分别为0.705、10.952、51.538 Hz,误差分别为1.13%、4.40%、9.21%。

图3 前4阶频率与跨数关系

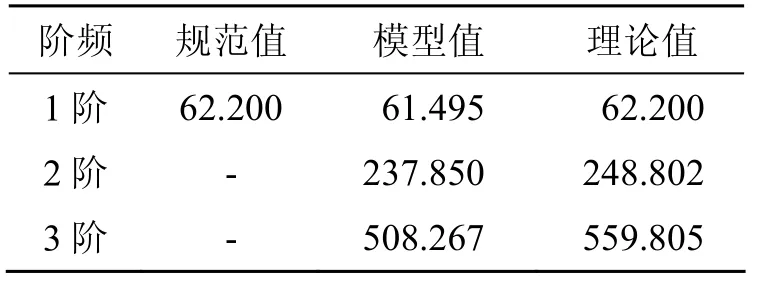
表3 简支梁频率计算结果 /Hz

3 现场T梁试验

某桥为整体式桥梁,与路线右夹角为90°,错幅布置,桥长为456.16 m,上部结构为5×30 m+3×50 m+5×30 m跨预应力砼T梁(先简支后结构连续)。下部构造为柱式墩配桩基、肋板台配桩基础,该桥桩基按嵌岩桩设计。

表4 某桥3×50 m跨频率测试结果 /Hz

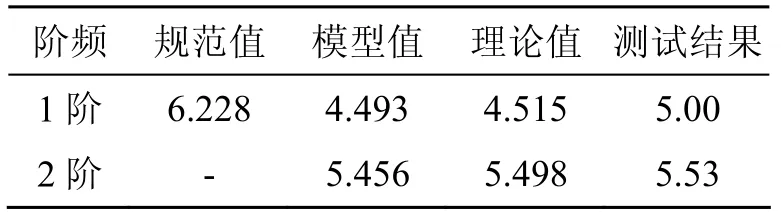
表5 某桥5×30 m跨频率测试结果 /Hz

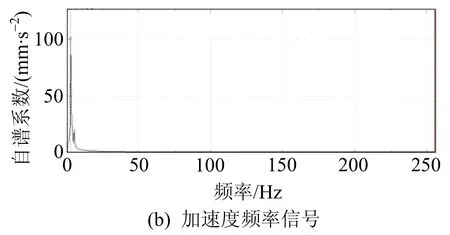
图4 3×50 m跨DASP频率测试

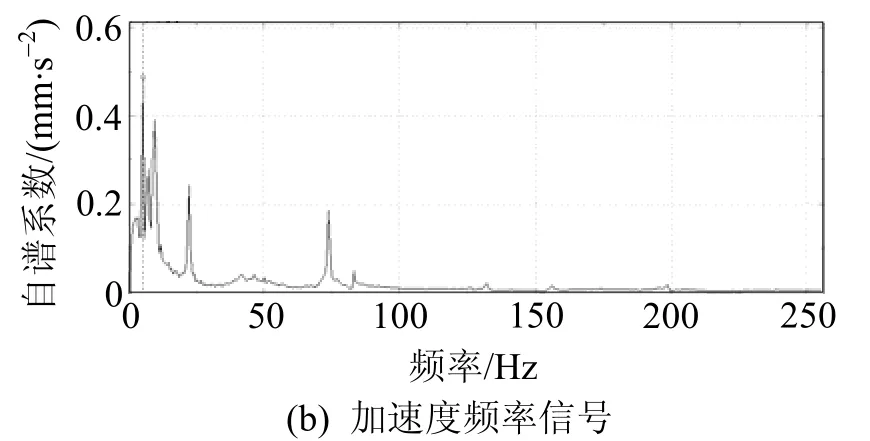
图5 5×30 m跨DASP频率测试

由表4可知,3×50 m跨梁采用规范推荐的连续梁桥计算公式计算时,基频相对误差达到38.28%,而采用规范推荐的简支梁基频计算公式计算时,相对误差仅为0.1%。由表5可知,5×30 m跨梁采用规范推荐的连续梁桥公式计算时,基频相对误差达到37.94%,而采用规范推荐的简支梁基频公式计算时,相对误差仅为0.1%。因此,等截面布置的连续梁桥,按相同跨径、相同截面简支梁桥的公式估算的基频,较规范给出的连续梁桥基频公式计算的结果更准确、可靠。

4 结论

本文通过理论分析,结合室内模型试验及现场T梁试验,探讨了等跨、等截面连续体系的频率,得到以下结论。

室内模型试验表明,采用《公路桥涵设计通用规范》推荐的连续梁计算基频公式,误差较大,已经不能满足工程精度的要求。通过计算发现,等截面的连续梁桥的基频接近于相同跨径、相同截面简支梁的基频;除基频外,其它阶次的频率随着跨数的增加,逐渐减小,当跨数趋于无穷大时,频率趋近于基频。

通过两联(3×50 m、5×30 m)工程实测表明,采用等截面布置的连续梁桥,其基频可按相同跨径、相同截面的简支梁桥的基频计算公式来近似估算基频,其结果比规范给出的连续梁桥基频计算公式准确、可靠。

[1] JTG D60—2015 公路桥涵设计通用规范[S].

[2] 任剑莹,苏木标,李文平,等. 铁路连续梁桥竖向有载自振频率研究[J]. 铁道学报,2005,27(5):111–116.

[3] 唐贺强,沈锐利. 简支梁桥有载频率分析[J]. 西南交通大学学报,2004,39(5):628–632.

[4] 苏木标,梁振辉. 对车—桥系统自振特性的初探[J]. 石家庄铁道学院学报,1993,6(3):49–58.

[5] 孙利民,闫兴非. 人行桥人行激励振动及设计方法[J]. 同济大学学报(自然科学版),2004,32(8):996–999.

[6] EN3—2008 Design of Footbridge Guideline [S].

[7] CJJ 69—1995 城市人行天桥与人行地道技术规范[S].

[8] 廖顺庠. 人行天桥的设计与施工[M]. 上海:同济大学出版社,1995:89–95

[9] 程永春,谭国金,刘寒冰,等. 基于特征解统计特性的桥梁损伤识别[J]. 吉林大学学报(工学版),2008,34(4):812–816.

[10] 陈政清,华旭刚. 人行桥的振动与动力设计[M]. 北京:人民交通出版社,2009:25–29.

[11] 施尚伟,赵剑,舒绍云. 梁桥冲击系数实测值与规范取值差异分析[J]. 世界桥梁,2010(2):79–82.

An accurate method of calculating frequency for continuous system with constant cross-section and constant span

Meng Yangjun1,Zeng Feiyun2
(1. Civil Engineering &Architecture College,Hunan University of Arts and Science,Changde 41500,China;2.CCCC Second Highway Consultant Co Ltd,Wuhan 430056,China)

A large number of engineering practices show that a first order vertical frequency of continuous T girder bridges which have been constructed first simply-supported after structural continuous is not in accordance with the first order vertical frequency calculated by "General Specifications for Design of Highway Bridges and Culverts"(JTG D60—2015). Therefore,the first order vertical frequency calculation formula of multi-span continuous girder bridge with constant cross-section and constant span is derived theoretically first. Second,combined with a two span and a three span constant cross-section continuous girder bridges,the finite element analysis and the theoretical calculation are compared with the specification calculation. Finally,combined with a practical continuous T girder bridge,the experiment and finite element analysis are compared with theoretical calculation.The results show that a first order vertical frequency of continuous girder bridge with constant cross-section and constant span is in accordance with the simply supported girder bridge with the same span and cross section.Through the theoretical analysis,the results show that with the number of spans increases,an-order natural vibration frequency (n≥2) of continuous girder bridge with constant cross-section and constant span decreases gradually. And when the number of spans tends to infinity,then-order natural vibration frequency (n≥2) reaches the first order vertical frequency.

constant cross section;continuous girder bridge;a first order vertical frequency

U 448

A

1672–6146(2017)04–0077–04

10.3969/j.issn.1672–6146.2017.04.019

孟阳君,352357749@qq.com。

2017–08–01

湖南省教育厅项目(16C1091);湖南文理学院校级课题(E07015017)。

(责任编校:刘晓霞)