非饱和岩土体中浅埋隧道稳定性的极限分析

李文涛,邓雄武

(云南工程建设总承包公司,云南 昆明,650000)

非饱和岩土体中浅埋隧道稳定性的极限分析

李文涛,邓雄武

(云南工程建设总承包公司,云南 昆明,650000)

自然土体大部分处于非饱和状态,而现有的隧道稳定性分析却假定土体是饱和的。为了研究土体的非饱和特性对隧道的影响,对非饱和土中浅埋隧道的稳定性进行了极限分析。基于非饱和土的Mohr-Coulomb强度准则和构建的浅埋隧道破坏机制,推导了围岩压力解析解。采用数值优化方法,计算了围岩压力的上限解。参数分析结果表明:基质吸力及埋深的增加有利于隧道的稳定,而地下水的存在不利于隧道稳定。

浅埋隧道;上限分析;非饱和土;围岩压力

近年来,地下空间的开发与利用成为城市基础设施建设的重点,分析与评估隧道的稳定性对于保障工程建设的顺利进行具有重要的意义。国内外学者针对隧道的稳定性问题进行了大量的研究,并提出了模型试验法、数值模拟法、极限平衡法和极限分析法等有效方法。在这些方法中,极限分析法具有严格的理论基础以及简单的求解过程,因此其被大量学者采用。Davis等[1]研究了软黏土中隧道的稳定性,并推导了不排水条件下稳定性系数的上、下限解。Osman等[2]提出了隧道塑性变形的机制,并得到了无衬砌隧道周边地表位移的上限解。Klar等[3]基于不可压缩场推导了二维和三维情况下软土地层中隧道开挖的上限解。Yang等[4]采用切线技术将非线性破坏准则引入到极限分析中,得到了浅埋隧道围岩压力的上限解。Fraldi和 Guarracino[5–6]基于塑性理论和变分法推导了深埋隧道拱顶破坏曲线的解析解。文献[7–8]构建了浅埋偏压与非偏压隧道的破坏模式,并研究了土体材料强度非线性以及地震力对隧道稳定性的影响。

上述研究都假定土体处于饱和或干燥的情况,然而自然土体大都是非饱和的。由于受基质吸力等因素的影响,非饱和土的力学性质与饱和土有很大的差别[9]。因此,基于饱和土力学性质的稳定性分析不能有效地反映隧道实际情况。鉴于此,本文采用Fredlund[9]所提出的非饱和土强度准则,对非饱和土中浅埋隧道的稳定性进行了研究。基于所构建的浅埋隧道的破坏机制,推导了围岩压力的解析解,并通过优化得到了围岩压力的上限解。参数分析所得的结论可以为实际隧道工程的建设提供参考。

1 基本原理

1.1 极限分析上限定理

1.2 非饱和土的抗剪强度

由于基质吸力的影响,非饱和土的强度特性与饱和土有很大的区别。Fredlund等[9]建议采用2个独立的应力状态变量来描述非饱和土的应力状态,并基于此提出了非饱和土的Mohr-Coulomb强度准则,其表达式为τ=c′+(σ-ua)tanφ′+ (ua-uw)tanφb。其中:c′和φ′分别为有效黏聚力和有效内摩擦角;(σ-ua)为净主应力;(ua-uw)为基质吸力;φb表示强度随基质吸力变化的摩擦角。由此可见非饱和土引入总黏聚力c=c′+(σ-ua)tanφ′后,强度准则表达式变为τ=c+ (σ-ua)tanφ′。Mohr-Coulomb强度准则与饱和土的相似。因此,相应的分析可以参照饱和土中隧道稳定性的分析方法。

图1 基质吸力随深度的线性分布

1.3 基质吸力的分布

自然土体中的基质吸力受土体水文特性和环境条件等诸多因素的影响,其随深度的分布规律十分复杂。但是当不考虑地面边界的降水和蒸发时,基质吸力的分布可近似为线性分布[11]。基质吸力在地下水面时为0,并往上逐渐增加(图1)。距地下水面z处的基质吸力可表示为(ua-uw)z=ρz。其中,ρ为基质吸力沿深度方向的变化率。

2 破坏机制的构建

现有文献中有许多浅埋隧道的破坏模式,其中最具代表性的为太沙基破坏模式和公路隧道设计规范所采用的破坏模式。Yang等[7]对该2种模式进行了对比,并结合实际工程经验,提出了一种更加合理的浅埋隧道破坏模式(图2(a))。该破坏模式将圆形隧道简化成矩形隧道,并假定隧道拱顶和底板的支护力为q,两侧边墙的支护力为e。q和e满足e=Kq,其中K为侧压力比例系数。隧道的埋深为H,洞径为h,地下水位线与隧道底板的垂直距离用z0表示。破坏机制中各速度矢量的关系如图2(b)所示。根据三角关系可得到如下的速度关系式v=cos(β+φ′)v0,v01=sin(α-β)v0/cos(α+2φ′),v1=cos(β+2φ′)v0/cos(α+2φ′)。其中:α和β分别为速度间断线CE和AC的倾角;φ′为土体的有效内摩擦角。

图2 浅埋隧道的平动破坏机制

3 围岩压力的上限分析

基于上述构建的浅埋隧道破坏机制,可以推导得速度场中的外力功率和内部能量耗散率。随后,根据极限分析上限原理,即可得到围岩压力的上限解。考虑到破坏机制的对称性,可取破坏机制的左侧部分进行研究,以简化推导过程。

3.1 外力功率的计算

3.2 内能耗散率的计算

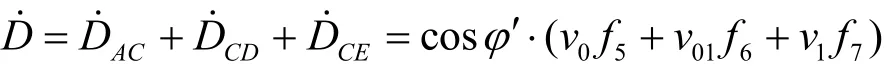
3.3 围岩压力的求解

根据极限分析上限定理,在任意满足速度边界条件的速度许可场中,由内部能量耗散率和外力功率相等所确定的荷载不小于真实的破坏荷载,可以得到围岩压力的解析解为q=(H2γv0f1+2Hhγv0f2+h2γv0f3– 2cosφ′(v0f5+v01f6+v1f7))/2hv0f4。此外,为了使破坏机制满足实际意义,参数α和β应该满足约束条件α-β＞ 0,π/2-α- 2φ′ ＞ 0,π/2+β+ 2φ′ ＞ 0。围岩压力的上限解即为满足该约束条件时,支护力q的最大值。这是一个数学优化问题,可通过序列二次规划算法或穷举法进行优化得到最优解。

4 参数分析

为了研究各参数对浅埋隧道围岩压力的影响,各参数的取值为:隧道埋深H=20 m;隧道洞径h=10 m;土体有效黏聚力c′=10 kPa;土体有效内摩擦角φ′=18°;与基质吸力有关的摩擦角φb=15°;基质吸力随深度变化率ρ=2 kPa/m;土体重度γ=20 kN/m3;侧压力比例系数K=0.85;地下水位z0=0。

4.1 基质吸力变化率对围岩压力的影响

通过优化计算,得到围岩压力q随基质吸力的变化规律如图3所示。由图3可知,基质吸力的变化对围岩压力q有较大的影响。随着基质吸力变化率的增加,围岩压力呈线性减小,且减小的幅度较大。与考虑基质吸力影响的计算结果相比,ρ=0所对应饱和情况的计算结果过于保守。此外,围岩压力也随有效内摩擦角的增大而减小。

图3 基质吸力变化率ρ对围岩压力的影响

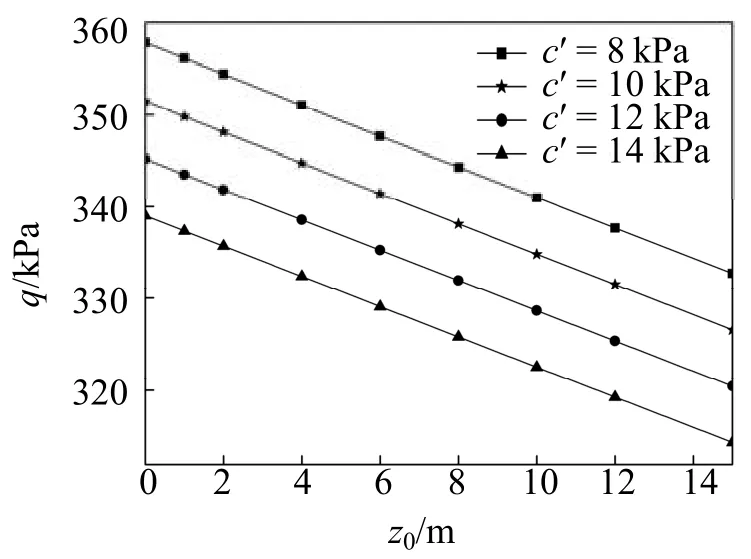
图4 地下水位高度z0对围岩压力的影响

4.2 地下水位高度对围岩压力的影响

地下水位高度影响着基质吸力的分布情况,因此其对浅埋隧道的稳定性也有一定的影响。通过计算得到围岩压力q随z0的变化规律如图4所示。由图4可知,围岩压力随着z0的增大而线性减小,但是其减小幅度相对较小。此外,围岩压力q随着有效黏聚力c′的增大而减小。

4.3 隧道埋深对围岩压力的影响

隧道的埋置深度也是影响其稳定性的一个重要因素。通过计算得到围岩压力q随着隧道埋深H的变化规律如图5所示。由图5可知,围岩压力q随H的增加而线性增加。其原因主要是当隧道埋深较大时,相应的地应力也较大。但是,过小的埋深会导致隧道坍塌事故的发生,因此实际隧道应选择合适的埋置深度。此外,还可以发现围岩压力q随侧压力比例系数K的增大而减小。

图5 隧道埋深H对围岩压力的影响

5 结论

本文采用非饱和土的Mohr-Coulomb强度准则来表征非饱和土的强度特性,基于所构建的浅埋隧道破坏模式推导了围岩压力的解析解,并通过数值优化方法计算得到了围岩压力的上限解。通过参数分析,得到了以下结论。

(1) 基质吸力的存在有利于隧道的稳定,围岩压力随着基质吸力变化率的增加而减少。与考虑基质吸力影响的计算结果相比,基于饱和土力学特性的计算是过于保守的。

(2) 地下水位高度也对围岩压力有一定的影响,围岩压力随着地下水位高度的增加而减少。因此在实际隧道的设计施工时应尽量让隧道远离地下水。

(3) 围岩压力随着隧道埋深的增加而增加,为了保证隧道的稳定性,应选择合适的隧道埋深。

[1] Davis E H,Gunn M J,Mair R J,et al. The stability of shallow tunnels and underground openings in cohesive material [J].Geotechnique,1980,30(4):397-416.

[2] Osman A S,Mair R J,Bolton M. On the kinematics of 2D tunnel collapse in undrained clay [J]. Geotechnique,2006,56(9):585-595.

[3] Klar A,Osman A S,Bolton M. 2D and 3D upper bound solutions for tunnel excavations using elastic flow fields [J].International Journal for Numerical and Analytical Methods in Geomechanics,2007,31(12):1 367-1 374.

[4] Yang Xiao-Li,Zhang Dao-Bing,Wang Z W. Upper bound solutions for supporting pressures of shallow tunnels with nonlinear failure criterion [J]. Journal of Central South University,2013,20(7):2 034-2 040.

[5] Fraldi M,Guarracino F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Science,2009,46(4):665-673.

[6] Fraldi M,Guarracino F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections [J].International Journal of Solids and Structures,2010,47(2):216-223.

[7] Yang Xiao-Li,Li Zheng-Wei,Liu Zheng-An,et al. Collapse analysis of tunnel floor in karst area based on Hoek-Brown rock media [J]. Journal of Central South University,2017,24(4):957-966.

[8] Yang Zi-han,Zhang Jia-hua. Minimum safe thickness of rock plug inkarst tunnel according to upper bound theorem [J].Journal of Central South University,2016,23(9):2 346-2 353.

[9] Fredlund D G,Rahardjo H. Soil mechanics for unsaturated soils [M]. New York:John Wiley and Sons,1993:179–183.

[10] Chen W F. Limit analysis and soil plasticity [M]. Amsterdam:Elsevier,1975:235–238.

[11] Zhang C G,Chen X D,Fan W. Critical embedment depth of a rigid retaining wall against overturning in unsaturated soils considering intermediate principal stress and strength nonlinearity [J]. Journal of Central South University,2016,23(4):944-954.

Upper bound stability analysis of shallow buried tunnels in unsaturated soils

Li Wentao,Deng Xiongwu
(Yunnan Engineering Construction Co Ltd,Kunming 650000,China)

Natural soil deposits are normally unsaturated,while existing researches on tunnel stability regard soil masses as saturated. In order to investigate the impact of soil’s unsaturated property on tunnel,limit analysis of stability of shallow buried tunnels in unsaturated soils is conducted. Based on the Mohr-Coulomb failure criterion for unsaturated soils and the constructed failure mechanism of shallow tunnels,the analytical solution of supporting pressure is deduced. Upper bound solution of supporting pressure is then obtained through numerical optimization.Conclusions of parameter analysis shows that matrix suction and the creasing burial depth are available to the stability of tunnel,but underground water is unavailable.

shallow buried tunnel;upper bound analysis;unsaturated soils;surrounding pressure

TU 45

A

1672–6146(2017)04–0089–04

10.3969/j.issn.1672–6146.2017.04.022

李文涛,116262819@qq.com。

2017–09–10

香丽高速项目(2017-315(3186))。

(责任编校:张红)