在馆读者的实时学习状态抽样分析与估算——以南京师范大学社科专业图书馆为例

邓盛,杨宇舟,朱全新

(1. 南京师范大学 图书馆,江苏 南京,210023;2. 厦门大学 经济学院,福建 厦门,361000;3. 南京师范大学数学科学学院,江苏 南京,210023)

在馆读者的实时学习状态抽样分析与估算
——以南京师范大学社科专业图书馆为例

邓盛1,杨宇舟2,朱全新3

(1. 南京师范大学 图书馆,江苏 南京,210023;2. 厦门大学 经济学院,福建 厦门,361000;3. 南京师范大学数学科学学院,江苏 南京,210023)

根据南京师范大学社科专业图书馆2016年4.22—5.22的在馆读者信息,以可反映学习状态的参数——在位人数、总占位数及吃零食、玩手机、用电脑、睡觉、交谈、学习等的人数,对该馆内读者的实时学习状态进行了抽样分析。首先,通过读者出入馆信息确定了状态参数的抽样时间为上午10—11时,并定义学风指标为学习人数除以实际在位人数;再对抽样时间点的学习状态参数及天气情况建立模型。通过建立负二项回归模型、广义线性模型,并应用稳健性检验方法得到了在馆读者的实时学习状态。结果表明:学风指标区间为60%～80%,处于良好状态;8—11时的进馆人数与学习氛围呈正相关关系,天气因素对馆内读书人数有较大影响,其是无法改变的外生变量,可通过改善图书馆的硬件设施与服务质量提升进馆人数;模型估计的学风指标与实际情况基本一致。

图书馆;实时学风;抽样调查;稳健性检验方法

学风是高校办学水平评估的重要指标[1],其可以通过学生读者在图书馆实时学习状态部分体现出来。目前,我国对学风建设的研究还处于一个较低的水平,主要集中在学风建设的加强及对策[2],也见于通过加强图书馆建设干预学风[3–6]。但对于学风的定量分析与研究鲜见。图书馆作为公共学习重要场所,其在内的自然的学习状态体现了读者的自我学习欲望[7],实时地反映了某一群体的学风状态。本文将以南京师范大学社科专业图书馆为例,用能反映学习状态的参数对馆内读者的实时学习状态进行抽样,并建立模型对图书馆内的实时学风进行定量分析。以期得到一些参量间的相互关系及对学风的影响,并为加强学风建设及制定提升入馆人数措施提供参考。

1 实时学风抽样统计与分析

本文拟从3个方面讨论馆内读者的实时学习状态。首先,筛选出入馆信息数据,选取非功利学习时间段在馆读者量相对稳定且最高的时间点进行持续抽样统计,得到图书馆读者的实时学习行为数据;其次,通过每天进馆流量实时数据对稳定时间点的实时学风进行统计调查,得到实时学习状态的样本区间;最后,通过模型估算学习氛围的范围值。

1.1 择取10—11时作为抽样时间的依据

当图书馆进出流量基本平衡且最小时,就可以认定其为当天数据最稳定的时间点,这个时点的数据最能体现读者在图书馆的实时学习状态。在抽样时间2016.4.22—2016.5.22中,图书馆进馆人数的分布如图1所示。图1显示,每天每小时平均进馆人数有明显波动;图中曲线代表了均值点的波动轨迹,而10—11时的均值正好处于全天中较平稳的低进出值。其它时间数据起伏波动较大(另外20—21时数据因21点闭馆,呈自然闭合时间),不具备数据分析上的普遍意义,因此,本文对10—11时的数据进行了抽样调查。

图1 2016年4月22日—5月22日8—21时平均进馆人数分布状况

1.2 10—11时学习状态抽样数据统计

在对10—11时学习状态的抽样中,统计了从2016年4月22日到5月22日为期1个月的数据。这个时间段正处于学生期中考试完结,而期末考试尚远,且无大规模行业认证考试的相对非功利性时期。本文以在位人数(seat)、总占位数(occup)及吃零食(snack)、玩手机(phone)、用电脑(computer)、睡觉(asleep)、交谈 (chat)、学习(learn)等读者人数为学习状态的统计指标,统计结果如表1所示。由表1可知,实际在座读者的平均数量(70.13人)少于总占位的平均数量(108.7人),这可能是由于跨坐、暂时不在座位、占座等现象增加了总占位的数量。因此,实际在馆读者应该大于在位人数,但小于总占位数。交谈、吃零食、玩手机、用电脑、睡觉的人都较少,在座学习的平均人数为48.63,超过总在位人数的一半。

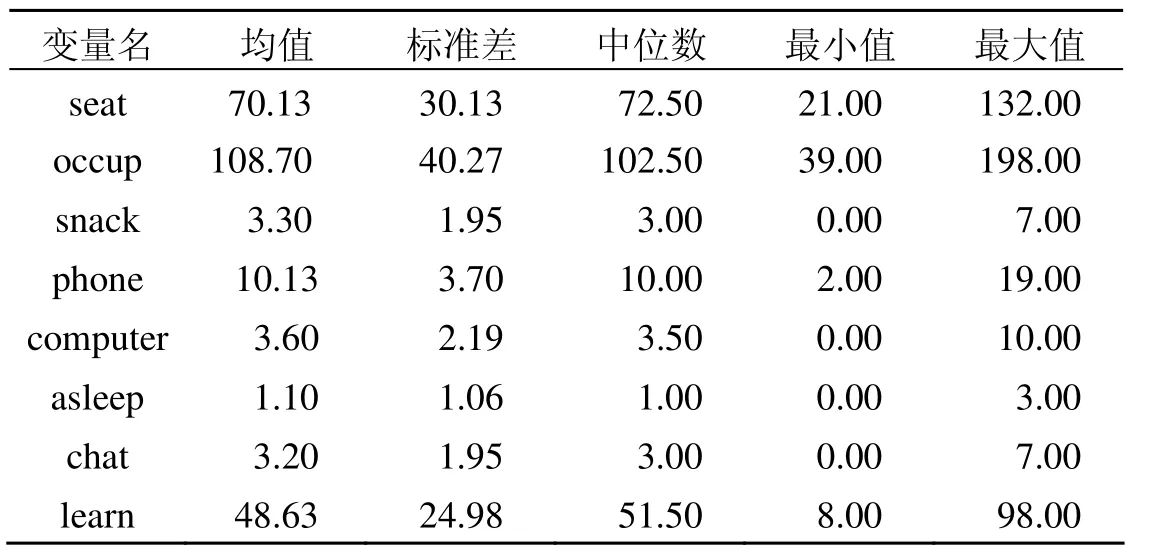
表1 不同行为读者的人数统计结果

用学习人数除以实际在位人数作为学风指标(Is)。则由表1可得到学风指标变化如图2所示。图2中剔除掉了节假日时间的数据,但为了数据在时间上的连贯性,保留了节假日的时间刻度,而没有显示相应数值。事实上即便考虑节假日时间的数据,趋势也不会发生明显的变化。由图2可知,1个月的实时学风指标稳定在60%～80%之间。

图2 2016年4月22日—5月22日10—11时学风指标变化趋势

2 模型选择与估值

2.1 负二项回归模型

由表1可知,平均在馆人数方差均值比为12.83,远大于1。那么学习人数数据存在过度分散(over dispersion)的特征,不满足进行泊松回归(Poisson Regression)的条件,因此选择负二项回归(Negative Binomial Regression)对数据进行分析。由文献[8]有负二项分布的密度函数

2.2 广义线性模型

2.3结果与分析

模型选择10—11时的实时学习状态指标进行分析。首先,从开馆时间到11时前的进出人数会对10—11时的学习人数产生影响;其次,图书馆的人数会受到天气与气温的影响;最后,周末与节假日也会影响图书馆人数,为此将周末时间剔除。

为防止因为模型选择而产生特定的偏误,故采用了3种不同的模型进行分析,即基准模型负二项回归、GLM框架下的泊松回归(泊松GLM)与负二项回归(负二项GLM)。

本文采用Stata12.0作为数据分析工具,根据文献[9]的方法,可以得到如表2所示的分析结果。由表2可知,前3个小时的进馆人数与图书馆的学风呈正向关系,其中8–9时进馆人数每增加1人,11时在馆的学习人数增加1.1%～1.4%;9–10时进馆人数每增加1人,11时在馆的学习人数增加0.75%～0.80%;而到了10–11时的进馆人数,对在馆学习人数的影响只有0.66%左右。因此,随着进馆时间越靠近抽样时间,进馆人数与学习氛围的关联越小。从上述回归结果可以得出,最低气温每上升1℃,会使图书馆读书人数上升8.5%～9.0%;下雨天要比不下雨的时候少30.7%～33.2%的学习人数。因此,外界环境对实时学习状态的影响要远超图书馆的内部环境影响。天气与气温都是无法改变的外生变量,进馆人数可通过改善图书馆的硬件设施与服务质量而得到提升。在考虑周末节假日的虚拟变量情况下,是否下雨对被解释变量的影响不再显著,这说明周末节假日的天气情况对被解释变量的影响有所不同。与其他自然因素比较(是否下雨、最低气温等),进馆人数对实时学习状态的影响要小得多,但它在评估学习氛围算法中的作用不可忽视,因为它是唯一能够人为调整的因素。

表2 学习人数的负二项回归与2种GLM回归分析结果

为了方便不同模型之间的比较,同时为了更直观地判断不同模型的拟合效果,给出实际值与估计值的协方差矩阵如表3所示。对拟合值与真实数据的相关系数矩阵进行分析,可以发现泊松GLM 的拟合效果最佳,但与其他2种方法的结果相差很小。

不同模型存在着系数波动,但不同模型中解释变量系数的正负性并没有发生变化,模型的显著性也没有发生变化,同一变量的不同系数大小也没有很明显的波动,因此,可以认为不同模型的拟合效果相似。

表3 实际值与估计值的协方差矩阵

2.4 稳健性检验

为了保证数据的稳健性,利用图书馆在位人数再次对上述模型进行分析。由于在馆学习人数必然属于图书馆在座人数,因此若用在座人数评估图书馆学习氛围,则会稀释真实数据,降低模型的解释力。在这种情况下,只要模型主要拟合系数的定性结论不发生变化,就可以判定模型对数据的解释力是比较稳健的。

在座人数的分析结果如表4所示。由表4可知,对于不同被解释变量,解释变量所拟合的参数性质(正负性)与学习人数的分析结果相比没有发生变化,只是对被解释变量(在座人数)的影响程度降低了。这种影响程度的降低,与降低的解释力是一致的:前3 h的进馆人数与图书馆学习氛围呈正向关系,其中8—9时进馆人数每增加1人,图书馆学习人数增加0.85%～0.87%;9—10时进馆人数每增加1人,图书馆学习人数增加0.64%～0.69%;10—11时进馆人数每增加1人,图书馆学习人数增加0.45%～0.48%。最低气温每上升1℃,图书馆读书人数上升8.3%～8.7%。对于是否下雨的虚拟变量,可以发现在正常时间段内,雨天的在座人数比不下雨时少23.4%～24.1%。

表4 在座人数的负二项回归与2种GLM回归分析结果

同理,在座人数分析的协方差矩阵如表5所示。表5与表3相比,拟合效果也要差一些,但泊松GLM的拟合效果仍然要比其他2个模型高一些。

表5 在座人数实际值与估计值的协方差矩阵

2.5 学习人数估计

通过以上不同模型对参数的估计结果,以及得到的估计值与实际值之间的相关系数,能粗略地描述学习氛围的波动情况。这为估算或者预测其他时间段的实时学习状态提供了参数。在利用社科图书馆2014年至2015年的相关数据,对实时学习状态进行估算时,首要是找到所有可能的解释变量,包括2014年至2015年对应时期的天气状况、8—11时进馆人数等。在此基础上,得到了图3所示的学习氛围估计值。

图3 2014与2015年4月22日—5月22日学习人数的不同模型估值

用不同模型估算在不同时间内的学习人数分布如图3所示。由图3可知,在估算的学习人数中,最多接近满员,出现在五一劳动节之后的2个星期中。最少人数小于50人,往往出现在周末。用同样的方法,也可以估算出不同年份相同时间段的图书馆在座人数,从而得到实时学风的估值。

2014与2015年4月22日—5月22日的实时学习状态百分比估计值分布如图4所示。由图4可知,学风百分比主要集中在60%～80%的区间内,并且学习状态随着周末与节假日出现呈周期性的上下波动。通常在节假日,图书馆的实时学习状态也到达最低值。3种不同估算方法的结果及拟合效果都非常接近,说明研究方法是可行的。

图4 2014与2015年4月22日—5月22日实时学风百分比估计值

3 结论

本文从出入馆信息数据入手,首先确定了上午10—11时作为抽样调查的基准时间,然后针对2016年4月22日到5月22日的图书馆读者行为进行了为期1个月的抽样统计。发现多数读者是在认真学习,学习状态指数维持在60%～80%之间,并且随着周末与节假日而发生波动。随后,本文根据天气、气温、图书馆显示的读者进入人数等数据,对图书馆学习状态进行了估计:不仅发现外在因素更大程度上影响读者的学习状态,而且发现每天的读者来馆数量也与图书馆学习状态息息相关。在此基础上,回顾2014—2015年的历史数据,拟合得到了图书馆在2014—2015年对应时间的学习人数与学习状态的状况。2年对应时间的估值结果显示,图书馆学风仍然处于60%～80%的区间内,并且随周末节假日的周期性变化明显。

[1] 任波. 论高校“三风”建设[J]. 重庆城市管理职业学院学报,2013,13(4):10-15.

[2] 张勇,荣翠琴,王玲. 试论高职院校图书馆的阅读推广模式—以成都航空职业技术学院图书馆为例[J]. 大学图书馆学报,2014,32(2):64-67.

[3] 杨剑瑜,杨文奎. 图书馆嵌入式服务信息资源整合平台的模型构建[J]. 湖南文理学院学报(自然科学版),2014,26(2):91-94.

[4] 段汶君. 试论高校图书馆导读的必要性和具体实施[J]. 图书馆工作与研究,2006(4):54-55.

[5] 马莉,惠调艳. 高校教学质量影响因素分析及其对策建议[J]. 西安电子科技大学学报(社会科学版),2011,21(2):98-101.

[6] 倪佳. 阅读推广与大学图书馆管理服务创新[J]. 湖南文理学院学报(自然科学版),2016,28(1):79-82.

[7] 刘秋林. 教育现代化进程中的高校图书馆[J]. 湖南文理学院学报(社会科学版),2005,30(1):107-109.

[8] Cameron A C,Trivedi P K. Regression analysis of count data [M]. Cambridge:Cambridge university press,2013.

[9] Long J S,Freese J. Regression models for categorical dependent variables using Stata [M]. College Station,Texas:Stata press,2006.

Analysis and estimation of learning style in Library

Deng Sheng1,Yang Yuzhou2,Zhu Quanxin3
(1. Library of Nanjing Normal University,Nanjing 210023,China;2. School of Economics,Xiamen University,Xiamen 361000,China;3. School of Mathematical Sciences,Nanjing Normal University,Nanjing 210023,China)

Based on the present readers’ information from Nanjing Normal University professional library between Apr 22th and May 22th in 2016,the readers’ real-time learning style are analyzed by some parameters reflecting learning status such as the present number,the total number of occupied seats,and the numbers of who are eating snack,playing phones,using computer,sleeping,talking and learning. Firstly,the readers’ entrance information are used to ensure that the sampling time of status parameters is 10—11 a.m. each day,and we define the learning style index as the number of who are learning divided by the real number of who are present seated. Secondly,a model is put forward based on the learning status parameters and weather conditions from sampling time point. By the Negative Binomial Regression,Generalized Linear Model and robust test,the real-time learning status of present readers is put forward. The results show that the interval of the learning style is 60%~80%,which is good;there is a positive correlation between the entrance number of 8—11 o’clock and the learning atmosphere. The weather condition is an unchanged exogenous variable that affects the number of readers. The improved library’s hardware facilities and service quality can increase the entrance number. The index made by the model is basically consistence with the actual circumstance.

Learning style;real-time learning style;sampling survey;robustness test method ;sample interval

G 251

A

1672–6146(2017)04-0018-05

10.3969/j.issn.1672–6146.2017.04.005

朱全新,05401@njnu.edu.cn。

2017–09–10

国家自然科学基金(61374080);江苏省自然科学基金(BR20161552)。

(责任编校:张红)