基于高精度测频的修正DFT相量及功率测量算法

谢运华，赵庆生，郭贺宏，张学军



基于高精度测频的修正DFT相量及功率测量算法

谢运华1，赵庆生1，郭贺宏2，张学军3

(1.太原理工大学电力系统运行与控制山西省重点实验室，山西 太原 030024；2.国网临汾供电公司，山西 临汾 041000；3.山西大学, 山西 太原 030006)

为了提高频率偏移时电力系统相量及功率测量精度，提出了一种基于改进扩展卡尔曼滤波(IEKF)频率测量的修正离散傅里叶变换(DFT)相量及功率测量算法。分析了频率发生偏移时非同步采样下DFT的测量误差，建立了相角、幅值与频率偏移量和初相角之间的函数关系式。由IEKF得到频率偏移量，然后对DFT计算结果进行修正即可得到输入信号的真实相量和功率。仿真结果表明：该算法相比较于传统自适应DFT算法能有效消除或减弱谐波、噪声以及频率偏移对相量同步测量的影响，提高了相量及功率测量精度。

离散傅里叶变换(DFT)；IEKF；非同步采样；相量测量；功率测量

0 引言

近年来，电能质量的监测问题得到了广泛的讨论，电力系统安全稳定运行成为人们关注的焦点。为了保证电力系统安全、稳定和高效的运行，有必要对电能质量进行监测分析，尤其是对基波信号的幅值、相角和频率的精确测量。这样，同步相量测量技术应运而生，而作为同步相量测量技术核心的同步相量测量算法，其精度直接影响到电力系统稳定控制、故障分析及继电保护等高级应用的准确性[1]。目前，常用的相量测量算法有卡尔曼滤波[2]、离散傅里叶变换(DFT)[3]、dq变换法[4]等等。

由于传统DFT算法易受频率波动和噪声的影响，造成非同步采样而导致频谱泄露和栅栏效应严重影响了其测量精度[5]。文献[6]提出了一种改进相位差的相量测量算法，该算法在频率偏移量计算上容易受低频振荡和谐波的干扰，从而限制了其应用。电力系统基频测量是相量和功率测量的基础，许多学者也提出了各种基频算法，像Prony算法[7]、牛顿类算法[8]等等。由于具有良好的滤波性能，各种线性、非线性的卡尔曼滤波方法得到越来越多的关注[9]。本文在传统EKF的基础上提出对模型噪声协方差矩阵进行自适应调整的改进EKF基频测量方法；分析了频率发生偏移时非同采样下DFT的测量误差，并建立了各个量之间的函数关系式，提出了对DFT计算结果进行修正的幅值、相角和功率测量算法。最后，通过仿真验证了算法的有效性。

1  IEKF基频测量原理

电力系统中离散电压信号表示为

由文献[9]可知基波信号三个连续采样点满足：

根据式(3)建立如下状态方程和观测方程：

由扩展卡尔曼理论得状态预测、更新过程：

其中：

由式(4)可得频率值的计算公式为

根据文献[10]的思想，本文在频率计算迭代过程中对模型噪声协方差矩阵进行自适应调整：

那么有：

2  非同步采样下DFT误差分析

由欧拉公式[11]，式(18)可以写成如式(20)所示。

图中：

图1系数分析

Fig. 1 Coefficient analysis

为了便于对幅值关系式的推导，可将式(28)进一步简化为

由正弦函数的泰勒级数展开式可得：

DFT算法的幅值和相角计算式为

3  功率误差分析

假设输入电压电流信号为

由功率计算公式可得有功功率、无功功率：

根据式(28)、式(32)同理可得电流相角和幅值的真值与DFT测量值的关系式；在得到电压、电流幅值和相角的真实值与误差值关系的基础上，根据式(36)计算真实有功功率和无功功率值。为减少计算量，需对有功、无功计算进行必要简化。

3.1有功率测量

不修正时，由DFT测量值直接计算有功功率：

3.2无功功率测量

同理可得DFT算法的无功功率计算式：

结合式(28)、式(32)，同理可将式(39)简化为

4 算法性能仿真结果及分析

本文所采用的仿真实验环境为：Matlab 2010a，32-bit win7系统，Pentium(R) Dual-Core 3.00 GHz。对信号的采样频率统一为2 000 Hz。

4.1 算例1

假设测试电压和电流信号数学模型如下所示。

4.1.1基波频率追踪效果

信号基波频率由48 Hz以0.1 Hz的步长变化到52 Hz。IEKF基波频率追踪结果如图2~图4所示。

图2频率追踪的收敛过程

Fig. 2Convergence process of frequency tracking

图3误差结果

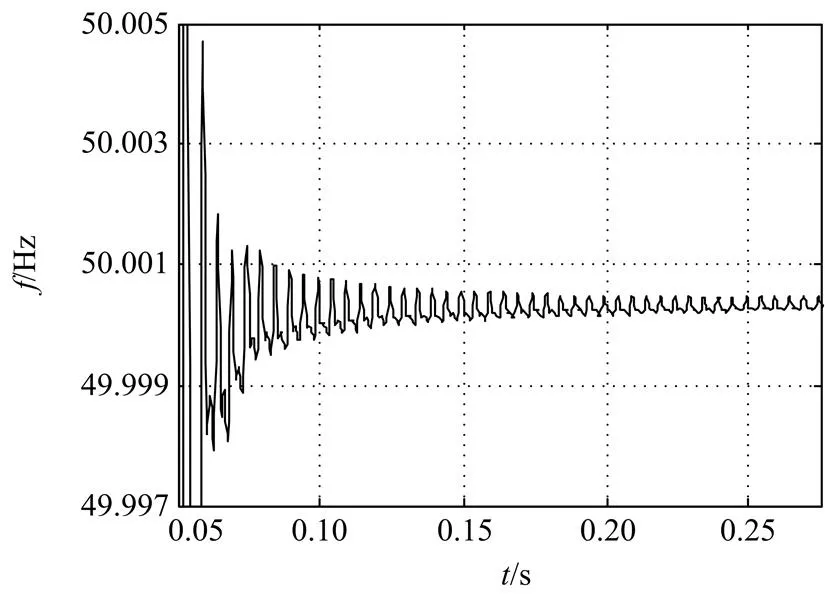
图4 50 Hz的频率追踪结果

(1) 图2为48 Hz、50 Hz、52 Hz的三种频率追踪结果随时间变化的情况。由图可知，当算法收敛时，频率测量曲线与真实值曲线几乎重合，说明IEKF频率算法能有效地追踪到基波频率的变化。

(2) 图3为算法稳定后，对48~52 Hz的频率跟踪误差，由图可知结果误差非常小，均小于0.002 Hz，可以满足电力系统的相关实际应用要求。

(3) 图4为算法收敛后，频率50 Hz追踪的局部放大图，由图可知频率跟踪精度非常高，误差小于0.001 Hz；大概在0.07 s的时候，频率的误差就被限制在了内，频率追踪速度非常快。

4.1.2修正非同步DFT相量测量算法

当频率取48~52 Hz不同值时，分别从幅值、相角误差对本文算法与文献[12]中自适应DFT算法进行对比，为避免重复，本文只对电压进行仿真，结果如图5~图8所示；图9和图10为两种算法所得到的有功功率和无功功率误差率的对比图。

相角、幅值误差的定义如下：

相角误差=测量值—真实值 (43)

幅值误差=(测量值—真实值)×100%/真实值 (44)

式中，真实值均指基波信号的相角、幅值真实值。

(1) 图5为信号基波频率由48~52 Hz变化时，两种算法的相角误差图；由图可知，相角误差在50 Hz附近最小，随着频率偏移量的增大误差值有所增大；自适应DFT算法的误差曲线更为陡峭，最大误差绝对值接近0.4º，而本文算法不到0.1º。

(2) 图6为基波频率变化时的电压幅值误差，同样自适应DFT算法的误差曲线较为陡峭，其最大误差绝对值接近4%，而本文小于0.5%；

(3) 图7为基波频率50.5 Hz下幅值测量结果图；由图可知两种算法的幅值误差都比较小，自适应DFT算法相对而言较大，其幅值误差最大处接近0.005；而本文算法的幅值误差不超过0.002。

(4) 图8为基波频率50.5 Hz下相角误差结果图；由图可知本文算法误差非常小，小于0.015º；而自适应DFT算法相角误差大于0.07º。

图7 50.5 Hz时电压幅值

图8 50.5Hz时电压相角

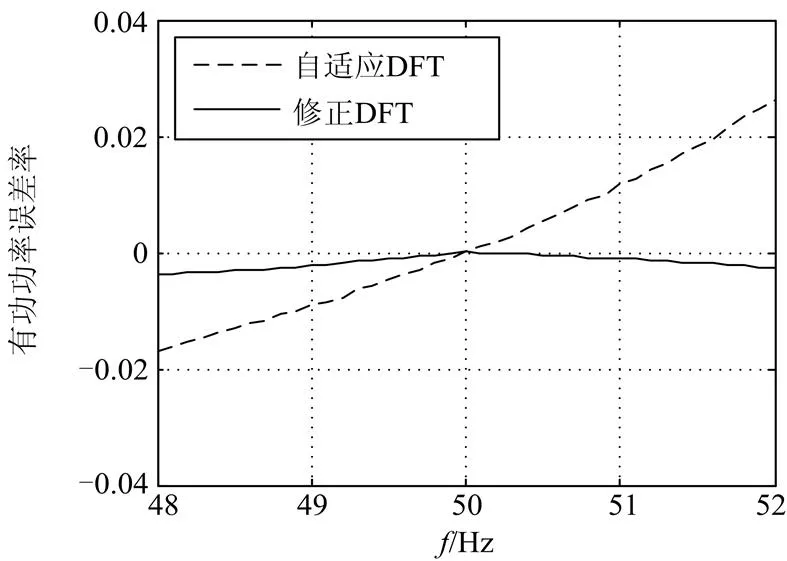
图9有功功率误差率

图10 无功功率误差率

(5) 图9为基波频率在48~52 Hz时有功功率误差率图；由图可知本文算法有功功率误差率曲线接近原点线，误差非常小；而自适应DFT算法的误差率随频率偏移量的增大，其最大值超过了0.02。

(6) 图10为基波频率在48~52 Hz时无功功率误差图；由图可知本文算法无功功率误差率很小，绝对值不超过0.001；而自适应DFT算法的误差率随频率偏移量的增大，最大绝对值超过了0.004。

4.2 算例2

假设电压、电流信号数学模型同式(41)、式(42)；式中为50.5 Hz，随时间在之间变化；实验仿真结果如图11~图13所示。

(1) 图11和图12为两种算法有功功率、无功功率误差率结果图；横坐标为信号电压、电流基波分量的相角差；由图11可知，本文算法所得误差率几乎与原点线重合，非常小；而自适应DFT算法的误差率超过了0.02；与有功功率误差率结果类似，由图12可知本文算法无功功率误差率几乎与原点线重合；自适应DFT算法误差绝对值超过了0.002。

(2) 图13为基波电压电流相角差变化时两种算法幅值误差百分比结果图；因本文算法精度非常高，故其误差曲线几乎与原点线重合，误差非常小；而自适应DFT算法的误差百分比的绝对值则超过了1%；由以上几点即可验证本文算法的有效性。

图11有功功率误差率

Fig. 11 Active power error rate

图12无功功率误差率

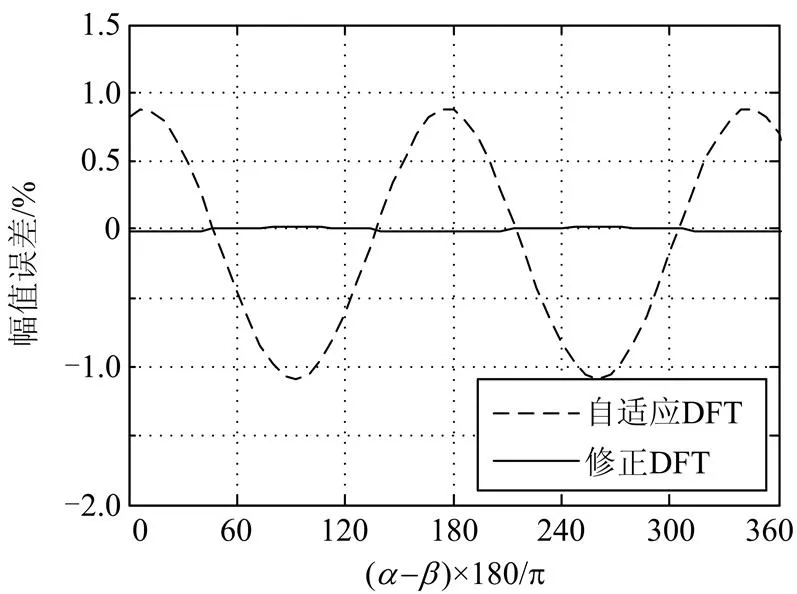
图13电压幅值误差

5  结论

在信号频率发生随机变化，且信号中含有谐波和噪声干扰时，本文所提出的基于IEKF频率精确跟踪的修正DFT算法原理简单，能对信号的同步相量和功率进行有效的测量，收敛速度快，虽然增加了一些有限的计算量，却在很大的程度上提高了传统的各种DFT算法所难以达到的精度，能满足电力系统的相关标准要求。

[1] 任先文, 谷延辉, 解东光, 等. 电网广域测量系统中PMU的研究与设计[J]. 继电器, 2005, 33(14): 52-56.

REN Xianwen, GU Yanhui, XIE Dongguang, et al.Research and design of the PMU of wide area measurement system in power system[J]. Relay, 2005, 33(14): 52-56.

[2] 吴智利,赵庆生, 陈惠英,等. 低频采样下基于卡尔曼滤波的同步向量测量算法的研究[J]. 电力系统保护与控制, 2014, 42(15): 94-99.

WU Zhili, ZHAO Qingsheng, CHEN Huiying, et al.A Kalman-filter based phasor measurement algorithm under low sampling frequency[J]. Power System Protection and Control, 2014, 42(15): 94-99.

[3] 吴梓亮,李银红,李明,等. 一种基于修正相角差的傅氏测频算法[J]. 电力系统保护与控制, 2015, 43(13): 111-117.

WU Ziliang, LI Yinhong, LI Ming, et al. Fourier frequency measurement algorithm based on modified phasor angle difference[J]. Power System Protection and Control, 2015, 43(13): 111-117.

[4] 常鲜戎, 王旋, 方学珍. 基波电流瞬时值检测及同步电流相量测量方法[J]. 电力系统保护与控制, 2013, 41(11): 60-66.

CHANG Xianrong, WANG Xuan, FANG Xuezhen. Fundamental current instantaneous value detection and synchronized current phasor measurement method[J]. Power System Protection and Control, 2013, 41(11): 60-66.

[5] BEGOVIC M M, DURIC P M, DUNLOP S, et al. Frequency tracking in power networks in the presence of harmonics[J]. IEEE Transactions on Power Delivery, 1993, 8(2): 480-485.

[6] WANG Maohai, SUN Yuanzhang. A practical method to improve phasor and power measurement accuracy of DFT algorithm[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1054-1062．

[7] LOBOS T, REZMER J. Real-time determination of power systemfrequency[C] // Instrumentation and Measurement Technology Conference, Brussels, Belgium, June 4-6, 1997: 877-881.

[8] REZA M S,CIOBOTARU M, AGELIDIS V G. Power system frequency estimation by using a Newton-type technique for smart meters[J].IEEE Transactions on Instrumentation and Measurement, 2014, 64(3): 615-624.

[9] ROUTRAY A, PRADHAN A K, RAO K P.A novel Kalman filter for frequency estimation of distorted signals in power systems[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(3): 469-479.

[10] MACÍAS J A REXPÓSITO A G.Self-tuning of Kalman filters for harmonic computation[J]. IEEE Transactions onPower Delivery, 2006, 21(1): 501-503.

[11] XIA Tao,LIU Yilu. Single-phase phase angle measurements in electric power systems[J].EEE Transactions on Power Systems, 2006, 25(2): 844-852.

[12]闵勇, 丁仁杰, 韩英铎, 等. 自适应调整采样率的相量在线测量算法研究[J].电力系统自动化, 1998, 22(10): 10-13.

MIN Yong, DING Renjie, HAN Yingduo, et al. Adaptive adjustment of sampling rate of the on-line phasor measurement algorithm research[J]. Automation of Electric Power Systems, 1998, 22(10): 10-13.

(编辑 姜新丽)

A modified DFT of phasor and power measurement algorithm based on high precision frequency measurement

XIE Yunhua1, ZHAO Qingsheng1, GUO Hehong2, ZHANG Xuejun3

(1. Shanxi Key Laboratory of Power System Operation and Control, Taiyuan University of Technology, Taiyuan 030024, China;2. State Grid Linfen Power Supply Company, Linfen 041000, China; 3. Shanxi University, Taiyuan 030006, China)

In order to improve the power system phase and power measurement accuracy when frequency offset, this paper presents a modified DFT of phasor and power algorithm based on improved expansion Kalman filter (IEKF) frequency measurement, the measurement error of DFT under nonsynchronous sampling caused by frequency offset is analyzed, and the function relationship between the phase, amplitude and frequency offset and initial phase angle is established. The frequency offset is obtained by IEKF, and then the DFT calculation results can be corrected to obtain the real phase and power of the signal. The simulation results show that theproposed method compared with the traditional adaptive DFT algorithmcan effectively eliminate or weaken the influence of harmonics, noise and frequency offset on the synchronized phasor measurement, and improve the precision of phasor and power measurement.

This work is supported by National Natural Science Foundation of China (No. 51505317) and Natural Science Foundation of Shanxi Province (No. 2015011057).

discrete Fourier transformation (DFT); improved extended Kalman filter; non-synchronous sampling; phasor measurement; power measurement

10.7667/PSPC151000

2015-06-15；

2015-08-17

谢运华(1990-)，男，硕士研究生，主要研究方向为电力系统建模与仿真；E-mail：dadizizi@163.com

赵庆生(1969-)，男，通信作者，博士，副教授，主要研究方向为电力系统运行与控制和电力系统建模与仿真。E-mail: zhaoqs1996@163.com

国家自然科学青年基金项目(51505317)；山西省自然科学基金项目(2015011057)