基于马尔可夫链筛选组合预测模型的中长期负荷预测方法
张栋梁,严 健,李晓波,任晓达,张金忠,张福来
基于马尔可夫链筛选组合预测模型的中长期负荷预测方法
张栋梁1,严 健1,李晓波1,任晓达1,张金忠2,张福来2
(1.中国矿业大学信息与电气工程学院, 江苏 徐州221008;2.赣榆区供电公司,江苏 连云港 222100)
在负荷预测的模型组合过程中,主要是根据历史数据的趋势恰当选择模型,再根据模型特点选择权重分配方法。针对灰色关联度满足要求的几种模型预测值分化较大的问题,从负荷数据的增长率无后效性这一特点出发,通过对原始数据增长率的分析,采用马尔可夫链划分区间,从几种满足精度要求的模型中筛选出两种进行组合预测,通过方差—协方差方法分配权重。经过该种方法的筛选,不仅可以更准确地选择组合预测模型的类型,而且具有较高精度。
马尔可夫链;筛选;灰色关联度;组合预测
0 引言
电力系统负荷预测是供电部门科学、经济、合理地管理电力系统的一项重要内容。对电力部门分配未来几年的工作任务,合理部署人力、物力资源,促进国民经济快速、稳定增长具有极为重要的意义。对于中长期负荷预测,其中涉及的因素多且复杂。对于同一增长趋势,可用多种模型对其评估,结合灰色关联度等评价指标,最终可以选择是采用单一模型还是组合模型。
而在预测过程中,对于近期有波动的负荷数据,即便是所选用模型的预测值满足评价指标的要求,所预测的结果也有可能相差较大。
如果不进行模型筛选而直接组合起来预测,将会大幅降低预测的精度。本文针对这种情况,运用马尔科夫算法处理历史数据中每两点的增长率,通过划分状态区间,提供了一种筛选模型的方法,可以更有针对性地选择模型并组合,以此提高预测精度。
1 组合预测模型
1.1 灰色预测模型
灰色预测模型是一种以灰色累加生成技术为基础的模型[1-4]。该模型具有对样本的需求量小,对历史数据的趋势无要求,运算方便等优点,其中以GM(1,1)模型较为常用。
利用最小二乘法解和:
其中:
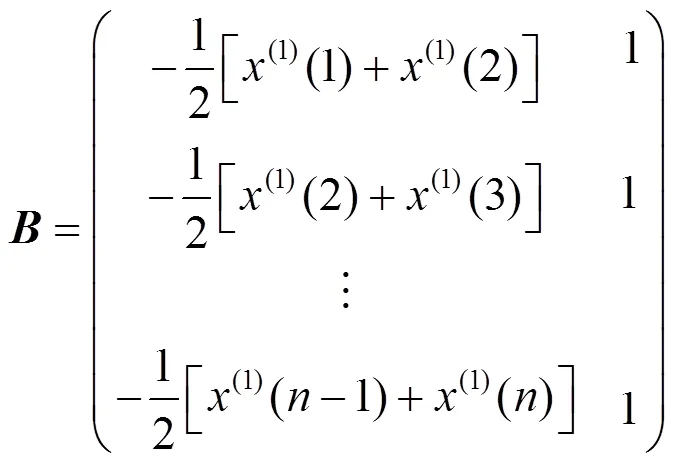
(4)
1.2 一元线性回归预测模型
线性回归预测模型是将统计学中回归分析理论和预测理论进行结合,当历史数据近似呈现线性趋势时,便可以通过对历史数据的分析,构建线性回归方程:
(5)
(6)
(7)
1.3 一元非线性指数模型
当历史数据的增长幅度近似呈现指数增长趋势时,也可采用非线性指数增长模型。一元非线性指数增长模型可以在一元线性回归预测模型的基础上通过两边取自然对数的方法求得。
两边取对数得:
(10)
1.4 二次指数平滑法
二次指数平滑法是在一次指数平滑的基础上再进行平滑处理,并以此得出预测模型的方法。二次指数平滑值记为,它是对一次指数平滑值计算的平滑值,即
二次指数平滑法的预测模型为
式中:
1.5 二次滑动平均法
二次滑动平均法和二次指数平滑法的求解过程类似,当历史数据具有近似线性性质时对其进行滑动平均处理。
二次滑动平均法的预测模型为
2 数据处理方法
2.1 马尔可夫预测法
马尔科夫预测方法是一种对无后效性随机事件序列进行分析的方法[5-9]。在电力系统历史电量数据中,其增长率只和当前两期的电量数据有关,即具备无后效性,因此可用马尔可夫链对数据进行处理。马尔科夫预测法的过程如下:
(1) 绘制时序曲线图;
(2) 根据经验进行状态划分;
(3) 计算初始概率和状态转移概率;
(4) 预测下一时刻的状态区间。
2.2 方差—协方差权重法
(19)
(20)
2.3 灰色关联度
灰色关联度是一种用来衡量两个系统间因素随时间或其他因素动态变化时,因素之间关联程度的概念[10-14]。
关联度作为一个衡量模型和原始数据贴近程度的概念,在负荷预测中意义重大。
3 实例研究
3.1 模型选择和精度检验
本文以某一区供电公司2003~2013年统计的电量为研究对象。根据历史数据的趋势,选择灰色预测模型、一元线性回归模型、一元指数增长模型、二次指数平滑和二次滑动平均模型。历史数据和五种单一模型的计算值见表1。
从历史数据可以看出,该地区电量在前期增长较为平稳,偶有降低趋势。2010年至2011年电量大幅增长,而2011年至2012年电量又开始下降。整体来看,属于非稳定增长序列。
为了检验所选用模型的准确性,采用2.3节中介绍的灰色关联度来衡量。选取2006~2013年数据代入,所得结果如表2 所示。
表1历史数据以及各模型数据
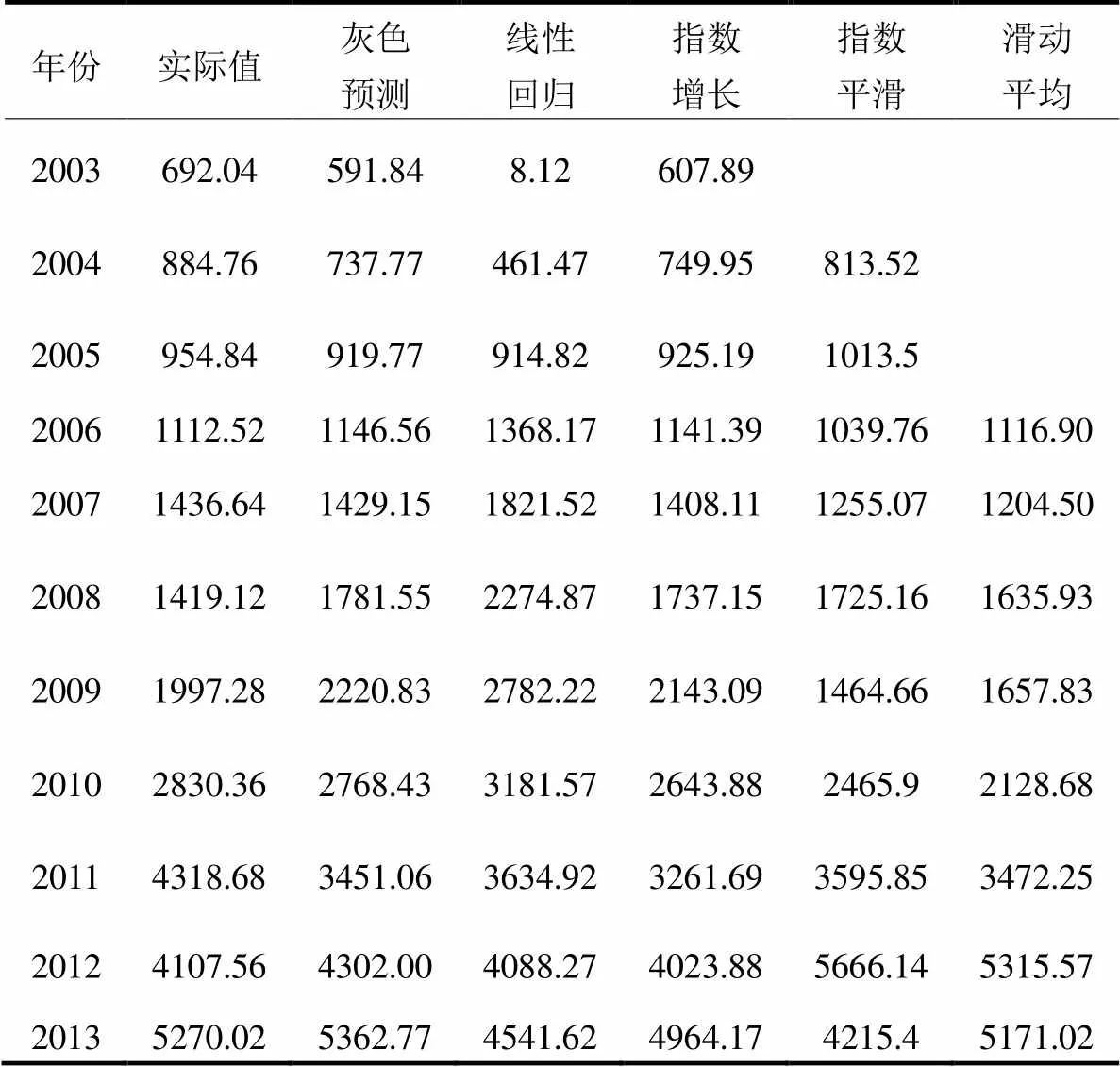
Table 1 Historical data and the data of each model GW·h
表2各模型的灰色关联度

Table 2 Grey relational degree of each models
从表2 可以看出:本文所选几种模型在精度上皆满足要求,可以用来预测2014年负荷。已知2014年实际负荷为5 387.40 GW·h。五种单一模型对2014年的预测值如表3所示。

表3 五种模型对2014年负荷的预测值
从表3可以看出:以上五种模型虽然在关联度上都能满足要求,但是预测出的结果相差较大。其中,灰色模型预测值较大,而线性回归和滑动平均模型预测值较小,指数平滑法和指数增长模型的预测结果居中。
在这种情况下,按照传统的组合预测方法,需要对各模型分配权系数。而文献[15]中提到权系数对于单一模型过于依赖的缺点,文献[16]也提到传统组合预测方法的缺陷。此时,如果直接组合预测,将对模型精度产生影响。
本文采用马尔科夫预测法,对原始数据每两点的增长率进行分析,得出概率转移矩阵,以2012~2013年的增长率预测2013~2014年增长率所处区间,从而可以从五种模型的预测结果中选择最终模型。
3.2 马尔科夫链预测增长率区间
由表1中各年份的实际值,可由11年数据得到10组增长率,增长率大小如表4所示。
表4历史数据每两点间增长率

Table 4 Growth rate between every two points of the historical load data
根据增长率状态,按照平稳(略微增长或降低)、一般增长和大幅增长三种状态,对增长率进行区间划分,划分的马尔科夫状态区域为:①[-10%,10%];② [10%,30%];③ (30%,)得到各状态初始概率如表5所示。
表5各状态初始概率

Table 5 Initial probability of each state
得到状态转移矩阵为

3.3 模型筛选
因为2012年至2013年的增长率处于第二状态,由无后效性原则和状态转移矩阵得:第二状态下一步将会有50%的几率进入第一状态,远高于进入第二状态的25%和第三状态的0%。
即2013年至2014年的增长率将会保持稳定。从而可以推断出,2014年的电量相比2013年的电量,将会略微下降或者持平,即便是增长,长幅也非常小。由此趋势判断,五种模型中,只有线性回归模型和滑动平均模型满足要求。
3.4 组合预测
将线性回归模型和滑动平均模型采用组合预测的方法。由方差—协方差公式(19)、式(20)得,,所以2014年的预测值为5 190.48 GW·h。
直接使用五种满足关联度的模型进行预测的结果和筛选后组合预测模型的精度对比见表6。
表6直接组合预测和筛选后组合预测结果对比

Table 6 Comparison of results between direct combination forecast and after screening combination forecast
由表6可知:经筛选后的组合预测模型在预测精度上有很大程度的提高。
4 结论
本文通过马尔科夫预测法,利用马尔可夫链筛选满足灰色关联度要求的模型,将筛选后模型利用方差—协方差法进行组合预测,使得组合预测模型的精度大幅提高。
本文中使用的马尔科夫链筛选方法,可以用来解决单一模型预测数据分化较大而不方便直接组合预测的问题,同时也为模型的选择提供了新的思路,更可以用来处理非平稳增长的负荷数据。
但本文所研究的数据不够多,未能总结出马尔科夫链筛选方法更深层次的规律,希望能在后续研究中加以改进。
[1] 牛东晓, 曹树华, 卢建昌, 等. 电力负荷预测技术及其应用[M]. 北京: 中国电力出版社, 2009.
[2] 鲁宝春, 赵深, 田盈, 等. 优化系数的NGM(1,1,)模型在中长期电量预测中的应用[J]. 电力系统保护与控制, 2015, 43(12): 98-103.
LU Baochun, ZHAO Shen, TIAN Ying, et al. Mid-long term electricity consumption forecasting based on improved NGM (1,1,) gray model[J]. Power System Protection and Control, 2015, 43(12): 98-103.
[3] 邢棉, 杨实俊, 牛东晓, 等. 多元指数加权电力负荷灰色优化组合预测[J]. 电网技术, 2005, 29(4): 8-11.
XING Mian, YANG Shijun, NIU Dongxiao, et al. Research on gray optimization combination load forecasting based on multivariate exponential weighting[J]. Power System Technology, 2005, 29(4): 8-11.
[4] 李霄, 王昕, 郑益慧, 等. 基于改进最小二乘支持向量机和预测误差校正的短期风电负荷预测[J]. 电力系统保护与控制, 2015, 43(11): 63-69.
LI Xiao, WANG Xin, ZHENG Yihui, et al. Short-term wind load forecasting based on improved LSSVM and error forecasting correction[J]. Power System Protection and Control, 2015, 43(11): 63-69.
[5] 张弘, 朱永佳, 范磊磊, 等. 基于马尔科夫修正的中长期电力负荷组合区间预测[J]. 华东电力, 2013, 41(1): 33-36.
ZHANG Hong, ZHU Yongjia, FAN Leilei, et al. Mid- long term load interval forecasting based on Markov modification[J]. East China Electric Power, 2013, 41(1): 33-36.
[6] JIA Jianrong, NIU Dongxiao. Application of improved gray Markov model in power load forecasting[C] // Electric Utility Deregulation and Restructuring and Power Technologies, 2008: 1488-1492.
[7] 郑文琛, 吉培荣, 罗贤举. 改进无偏GM(1,1)模型及其在中长期电力负荷预测中的应用[J]. 继电器, 2008, 36(5): 36-39.
ZHENG Wenchen, JI Peirong, LUO Xianju. An improved unbiased GM(1,1) model and its application in mid-long term electric load forecasting[J]. Relay, 2008, 36(5): 36-39.
[8] 张大海, 江世芳, 史开泉. 灰色预测公式的理论缺陷及改进[J]. 系统工程理论及实践, 2002, 22(8): 140-142.
ZHANG Dahai, JIANG Shifang, SHI Kaiquan. Theoretical defect of grey prediction formula and its improvement[J]. Systems Engineering-Theory & Practice, 2002, 22(8): 140-142.
[9] 王允平, 黄殿勋, 熊浩清, 等.智能电网环境下采用关联分析和多变量灰色模型的用电量预测[J]. 电力系统保护与控制, 2012, 40(1): 96-100.
WANG Yunping,HUANG Dianxun, XIONG Haoqing, et al. Using relational analysis and multi-variable grey model for electricity demand forecasting in smart grid environment[J]. Power System Protection and Control, 2012, 40(1): 96-100.
[10] EI-FOULY T H M, EI-SAADANY E F, SALAMA M M A. Grey predictor for wind energy conversion systems output power prediction[J]. Power System, 2006, 3(21): 1450-1452.
[11] 周德强. 基于最小一乘法的GM(1, 1)模型及在负荷预测中的应用[J]. 电力系统保护与控制, 2011, 39(1): 100-103.
ZHOU Deqiang. GM(1, 1) model based on least absolute deviation and its application in the power load forecasting[J]. Power System Protection and Control, 2011, 39(1): 100-103.
[12] 张成, 滕欢, 付婷. 基于灰色离散Verhulst模型理论的电力中长期负荷预测研究[J]. 电力系统保护与控制, 2013, 41(4): 45-49.
ZHANG Cheng, TENG Huan, FU Ting. Middle and long term power load forecasting based on grey discrete Verhulst model's theory[J]. Power System Protection and Control, 2013, 41(4): 45-49.
[13] 马哲, 舒勤. 基于ESPRIT分解算法的短期电力负荷预测[J]. 电力系统保护与控制, 2015, 43(7): 90-96.
MA Zhe, SHU Qin. Short term load forecasting based on ESPRIT integrated algorithm[J]. Power System Protection and Control, 2015, 43(7): 90-96.
[14] 陈剑勇, 苏浩益. 结合支持向量机和马尔可夫链算法的中长期电力负荷预测模型[J]. 南方电网技术, 2012, 6(1): 54-58.
CHEN Jianyong, SU Haoyi. A forecasting model of medium/long term power load in combination of the support vector machine and Markov chain algorithms[J]. Southern Power System Technology, 2012, 6(1): 54-58.
[15] 毛李帆, 姚建刚, 金永顺, 等. 中长期电力组合预测模型的理论研究[J]. 中国电机工程学报, 2010, 30(16): 53-59.
MAO Lifan, YAO Jiangang, JIN Yongshun, et al. Theoretical study of combination model for medium and long term load forecasting[J]. Proceedings of the CSEE, 2010, 30(16): 53-59.
[16] 龙瑞华, 毛弋, 毛李帆, 等. 基于诱导有序加权平均算子和马尔可夫链的中长期电力负荷组合预测模型[J]. 电网技术, 2010, 34(3): 150-156.
LONG Ruihua, MAO Yi, MAO Lifan, et al. A combination model for medium-and long-term load forecasting based on induced ordered weighted averaging operator and Markov chain[J]. Proceedings of the CSEE, 2010, 34(3): 150-156.
(编辑 周金梅)
Mid-long term load forecasting based on Markov chain screening combination forecasting models
ZHANG Dongliang1, YAN Jian1, LI Xiaobo1, REN Xiaoda1, ZHANG Jinzhong2, ZHANG Fulai2
(1. School of Information and Electrical Engineering,China University of Mining &Technology, Xuzhou 221008, China; 2. Ganyu District Power Supply Company, Lianyungang 222100, China)
It is important to choose the right model according to the trend of the historical data in the process of load forecast model combination. And then, a method is chosen to assign weights according to the features of the models. Even forecast models meet the requirements of the grey correlation degree, the forecast results still have large differences. To solve the question, this paper, according to the feature that the growth rate of load data isnon-aftereffect property of Markov chain, and by analyzing the growth rate of load data, uses Markov chain to divide intervals and screens two kinds from the models which have met the accuracy requirement, and adopts the method of variance- covariance to assign weights. Using this method of screening not only can accurately choose the models for combination forecast, but also has a high precision.
This work is supported by National Natural Science Foundation of China (No. 51107143).
Markov chain; screen; grey relational degree; combination forecast
10.7667/PSPC151217
2015-07-14;
2015-09-08
张栋梁(1975-),男,博士,副教授,研究方向为轨道交通杂散电流的治理与配电安全;
严 健(1990-),男,通信作者,硕士研究生,研究方向为电力系统负荷预测。E-mail: 328482321@qq.com
国家自然科学基金(51107143)

