利率期限结构、相对因子与汇率预测

李　艳， 吴　亮

（阜阳师范学院 a.数学与统计学院；b.经济学院，安徽 阜阳 236037）

利率期限结构、相对因子与汇率预测

李艳a， 吴亮b

（阜阳师范学院 a.数学与统计学院；b.经济学院，安徽 阜阳 236037）

由于利率期限结构中包含未来经济运行的信息，利用2006年4月到2014年12月中美两国利率期限结构的月度数据，通过动态Nelson-Siegel模型抽取两国利率期限结构的相对水平，斜率和凸度三因子，基于三个相对因子检验其对人民币/美元汇率的预测能力。实证研究表明：（1）相对因子模型对汇率在1到12月期具有可预测性，相对水平因子或相对斜率因子增加1%分别导致人民币升值1%和2%而相对凸度因子增加1%会导致人民币贬值1%；（2）基于CW检验统计量的滚动窗预测表明：在所考虑的各个滚动窗下，相对因子模型预测能力优于随机游走和非抛补利率平价模型。

利率期限结构；动态Nielsen-Siegel模型；相对因子；汇率预测

汇率的决定和预测一直是经济文献中探讨的焦点问题，经典的汇率决定理论将汇率当成资产，其为各种宏观经济变量的贴现值，因此理论上汇率与宏观经济基本面有着直接的关系。然而Meese和Rogoff［1］的研究发现，在预测区间小于一年的范围内，随机游走模型在预测汇率变动时要好于宏观经济模型，这种汇率与宏观经济基本面的脱离关系也就成为国际经济学的一个谜。此后，Cheung等［2］发现在少于一年的预测期间内没有发现任何模型的预测能力能优于随机游走模型，Rossi［3］对利用宏观信息进行汇率预测的模型和方法进行了评述。国内研究方面，陈平和李凯［4］对宏观经济信息与人民币汇率之间的关系进行了考察，在四种汇率决定的宏观经济模型中，只有一种模型的预测能力明显优于随机游走模型。

利率期限结构是指在某一时点上，债券到期期限和到期收益率之间的关系，又称收益率曲线，是资产定价、金融产品设计、保值和风险管理、套利以及投机等的基准。利率期限结构的变动与宏观经济走势具有密切的联系，Estrella和 Hardouvelis［5］认为十年期国债与三个月国债之间的利差是预测经济衰退可能性的一个有用指标；Haubrich和Dombrosky［6］发现长短期利差是对未来四个季度经济增长的极好预测指标。就中国利率期限结构与宏观经济变量之间的相关性问题而言，近年来得到长足的研究，郭涛和宋德勇［7］基于Nelson-Siegel模型的研究结果显示，中国利率期限结构所隐含的远期利率可以预测未来利率，其水平因子对未来通胀有预测能力，长短期利差较好地反映了货币政策状态。李宏瑾等［8］研究了中国银行间市场国债利率期限结构对通货膨胀的预测能力，发现中国短期利率期限结构（特别是中短端）包含了未来通货膨胀变动的信息，因而可以作为判断未来通货膨胀走势的预测变量。

我国在2005年7月21日对人民币汇率制度进行了改革，提出建立以市场需求为基础，参考一篮子货币进行调节、有管理的浮动汇率制度，人民币汇率与宏观经济基本面走势更为紧密。基于利率期限结构中含有宏观经济的信息，本文利用Diebold和Li［9］提出的动态Nelson-Siegel模型，构建中美两国利率期限结构的相对因子模型，研究的问题是利率期限结构是否具有预测未来人民币汇率变化的信息价值，以探讨利率期限结构在国际金融领域的应用，为市场参与者规避汇率风险以及货币政策当局对汇率的调控提供借鉴。

1　动态Nelson-Siegel模型与汇率预测

当市场上交易的债券期限结构不完整，需从现有的零息债券和附息债券价格中提取出所有期限对应的即期利率，从而可构造完整的利率期限结构，Nelson和Siegel［10］利用指数函数的衰减特性构造了包含四个参数的静态利率期限结构模型（简称NS模型）：

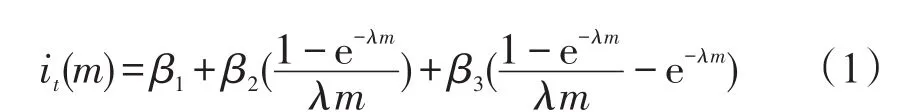
其中，β1，β2，β3为模型参数，λ决定指数的衰减速度，m为以月表示的债券期限。NS模型因其参数简化和估计结果的稳定性，已被各国中央银行广泛用于拟合利率期限结构，然而NS模型是一种静态拟合的参数方法，无法捕捉利率期限结构的动态特征。针对这一问题，Diebold和Li扩展Nelson和Siegel的研究框架，将式（1）静态NS模型中的参数β1，β2，β3看做随时间变化的三个动态因子，以此来刻画利率期限结构的时变特征，称为动态Nelson-Siegel模型（DNS模型），其形式如下：

其中，Lt，St和Ct可以理解成利率期限结构随时间变化的水平、斜率和凸度因子。由于参数λ决定指数的衰减速度，一方面，λ较小时，可对短期利率更好拟合；另一方面，λ较大时，可对长期利率更好拟合，此外λ决定Ct在何处达到最大。Lt的系数为1，说明其不会衰减到0，可看做长期因子；St的系数由1开始但会迅速单调衰减到0，可看做短期因子；Ct的系数由0开始随后增加，然后衰减到0，因此可看做中期因子。

利用两国利率信息进行汇率预测的典型模型是非抛补利率平价（uncovered interest rate parity，UIRP）模型，UIRP是指投资者可通过一单位本国货币购买1/St单位的外国债券，其中St为本国货币表示的外币价格。令外国债券在t到t+m的收益率为，在投资期结束时，通过投资外国债券所得到的本利和转化为本国货币为St。在套利和不存在交易成本条件下，投资外国债券所得收益与本国债券所得相同，设本国债券收益为it（m），则有：

其中，Et（·）表示t时刻的期望算子。对上式两边取对数，忽略Jensen不等式，可得到如下经验形式：

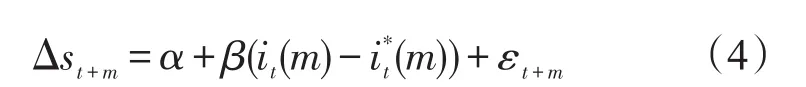
其中，LR，SR和CR为两国利率期限结构的相对水平，斜率和凸度三个因子。基于相对因子LR，SR和CR，构建如下汇率预测回归模型：

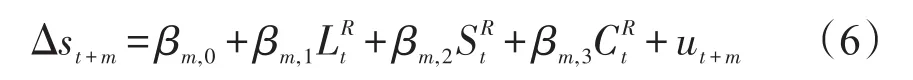
通过利率期限结构，依据DNS模型构建的相对因子对汇率进行预测，能够利用整个利率期限结构的信息。相对因子方法采用所有期限利率差分，显著扩大UIRP模型，相较于将每一期限利率差分纳入UIRP模型方程，相对因子方法能够明显降低维数，且各个因子具有合理的宏观经济解释。

2　实证研究

2.1数据来源和相对因子估计

汇改始于2005年7月21日，考虑数据可得性，本文选取的数据范围为2006年4月到2014 年12月，共计105个月度数据。在利率期限方面，分别选取了3，6，12，24，36，60，84和120月，共8个期限的利率，其中国内选取的是中债国债到期收益率曲线，数据来源于WIND数据库，美国选取的是美国国债收益率，数据来源于美国联邦储备委员会，人民币对美元名义汇率来源于WIND数据库，上述数据均为月最后一个交易日的数据。此外为使UIRP模型在1月期向前预测可同相对因子模型进行比较，同时选取了中美两国1月期短期利率，其中，美国短期月利率为联邦基金利率（Federal Fund rate），数据来源于美国联邦储备委员会，中国1月期利率为全国银行同业拆借30天到期的平均利率，数据来源于中国人民银行网站。

图1给出中美两国利率期限结构随时间变化的示意图。由图1可知，从整体形态来看，在样本期内美国国债收益率曲线整体上呈现向上倾斜的形态，而中国国债的收益率曲线呈现上升、拱形和水平三种形态。从波动性和连续性来看，美国国债收益率曲线除量化宽松货币政策开始实施阶段出现大幅跳跃外，总体上随着时间推移呈现连续、渐进的变化特征，相较而言，中国收益率曲线上下起伏较大，部分时期出现跳跃、突变的情形。

图1　中美两国利率期限结构示意图

估计DNS模型中参数的方法有非线性最小二乘和极大似然法等，这两种方法在实施过程中通常遇到数值优化问题，因此Diebold和Li建议固定λ等于0.060 9，采用OLS方法估计DNS模型参数，这样做的结果只是损失了很小的估计优度，却使得模型估计，尤其是动态估计变得简单易行，而且保证了各个因子在不同时间具有可比性。同样Chen和Tsang［11］基于两国相同期限的利率差分构建相对因子时，利用λ的经验值0.060 9进行参数估计。本文依据上述学者的相同方法，设定λ等于0.060 9，对式（5）利用OLS方法得到两国利率期限结构相对的水平、斜率、凸度三个因子。表1给出了三个相对因子的描述统计结果。

由表1中可看到，LR具有最大的均值且其波动最小，CR的均值最小且波动最大，三个因子的峰度系数均大于2接近于3且偏度较小，因此三个因子分布总体呈现出一定的右偏特征；JB统计量拒绝SR和CR正态分布的假设；最后通过相关系数发现，SR和CR的相关系数高达0.8，SR，CR与LR呈现出正相关关系，但相关系数低于0.4。

为分析相对因子在样本内对汇率是否具有可预测性，选取全部样本数据，通过式（6）进行回归分析。由于使用重叠数据进行长期预测分析时通常会导致推断偏差，当式（6）中的m超过1，会导致式（6）中的ut+m为m-1阶移动平均过程，这样统计量如标准差是有偏的，通常的做法是采用Newey-West标准误差就行纠正，然而Newey-West标准误差调整会导致严重的显著性扭曲。Valkanov［12］建议通过标准t统计量乘以得到的刻度化t统计量，纠正长期回归推断偏差，且刻度化t统计量具有近似正态分布。表2在m=1，3，6和12期，给出相对因子的系数估计和相应刻度化t统计量值。由表2中刻度化t统计量知，相对水平，斜率和凸度因子在所考虑的各个期限对汇率变动均具有显著解释能力，尽管相对水平因子仅在10%显著性水平上显著。由反应相对因子影响大小的系数上看，相对水平因子各期系数为正且接近1，意味着相对水平因子增加1%会导致人民币年升值1%；相对斜率因子在各期为正且接近2，从而相对斜率因子增加1%会引起人民币年升值2%，相对凸度因子各期系数为负且接近-1，从而相对凸度因子增加1%会引起人民币贬值1%。

表1　相对因子的描述性统计特征和相关系数

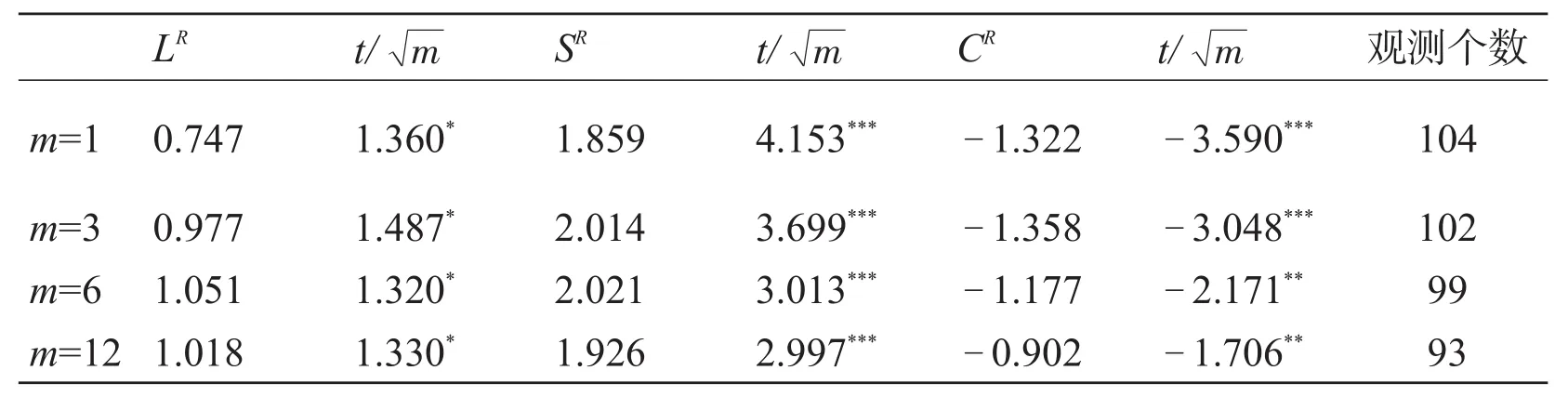
表2　相对因子对汇率的可预测性分析

2.2汇率预测与评价

通过上述全样本回归分析发现相对因子模型对汇率具有可预测性，下面分析相对因子模型对汇率的样本外预测能力，同时与随机游走模型和UIRP模型进行比较。在进行预测时，采用更能体现参数动态变动的滚动方法，在滚动窗为R时，模型参数使用最近R个观测进行估计，据此得到预测模型的m期样本外预测误差，而随机游走模型的m期预测误差为eRW，t+m=Δst+m。对模型预测进行评价通常采用预测误差的平方均值即MSFE （mean squared forecast error），除直接比较MSFE外，还可采用预测模型与基准模型的RMSFE （root mean squared forecast error）之比的Theil's U （TU）统计量，进行分析，如果TU＜1且显著，表明汇率模型预测能力优于随机游走模型。

为比较检验两个预测模型预测效果是否有显著性差异，采用Clark和West［13］提出的检验统计量。设模型1为节俭模型，模型2为约束模型，模型1和模型2在t时刻对 yt+τ的预测为 y^1t，t+τ和，预测误差分别为相应的 MSPE为和

基于 ft+τ，Clark和West提出的检验统计量为：

为分析样本窗宽对预测的影响，本文选取R= 36，48，［T/2］和60，预测期为m=1，3，6和12月，表3a和b分别给出相对因子模型与随机游走和UIRP模型的比较结果。首先，分析表3a中的结

果。由表3a可知，在滚动窗宽R=36和48时，各预测期的TU统计量均小于1（除去R=36，m=1和3时，TU分别为1.031和1.006，均接近于1），意味着相对因子模型具有更低的RMSE；在R=［T/2］和60时，TU在大部分预测期均大于1（除去R= ［T/2］，m=1，3和R=60，m=12外）；在各个滚动窗和预测期下，CW统计量均大于0且在5%以上显著性水平显著，意味着相对因子模型优于随机游走模型。

其次，分析表3b的结果。由表3b可知，在滚动窗宽R=36和48时，当R=36，m=1和R=48，m= 1和3时，TU统计量接近与1，其他情形TU统计量均小于1，CW统计量均在5%及以上显著性水平显著大于0；在滚动窗宽R=［T/2］和60时，在各预测期TU统计量均大于1，其最大为1.284，最小为1.002。当R=［T/2］，CW检验统计量在10%及以上显著大于0而R=60情形下，CW统计量在m=6时为-1.136，其余情形下均大于0，但无论正负均不显著，意味着此时UIRP模型和相对因子模型具有相同预测绩效。

综合以上分析，基于CW统计量发现相对因子模型对汇率的预测能力要优于随机游走模型和UIRP模型，特别是在滚动窗宽R=36和48时，TU统计量也小于1，因此在实践应用相对因子模型预测汇率时，采用相对小的滚动窗宽可得到更好的预测效果。

3　结束语

汇率变动与宏观经济基本面的关系一直都是国际经济学的一个中心问题，大量文献基于宏观经济基本面信息解释汇率的变动。考虑到利率期限结构在宏观层面上，具有预测未来经济增长，通货膨胀等一些主要宏观经济变量的信息价值，本文利用Diebold和Li提出的DNS模型，构建中美两国利率期限结构的相对DNS模型，从中提取相对水平，相对斜率和相对凸度因子，同时分析三个相对因子与汇率变动之间的动态关系。

本文研究得到以下结论：第一，相对水平，斜率和凸度因子在所考虑的各个期限对汇率变动均具有显著解释能力，相对水平因子增加1%会导致人民币年升值1%，相对斜率因子增加1%引起人民币年升值2%而相对凸度因子增加1%导致人民币年贬值1%；第二，基于CW统计量发现相对因子模型对汇率的预测能力要优于随机游走模型和UIRP模型，特别是在滚动窗宽R=36和48时，TU统计量也小于1，所以在实践应用相对因子模型预测汇率时，采用相对小的滚动窗宽可得到更好的预测效果。因此无论是在样本期间内还是在样本期间外，利率期限结构对人民币汇率变动都有良好的预测能力，此结论对货币当局制定政策具有重要的参考价值。

［1］ Meese R，Rogoff K.empirical exchange rate model of the 1970's：do they fit out of sample［J］.Journal of International Economics，1983，14（1/2）：3-24.

［2］ Cheung W Y，Chinn M D，Pascual A G.Empirical exchange rate models of the nineties：are any fit to survive？［J］.Journal of International Money and Finance，2005，24（7）：1150-1175.

［3］Rossi B.exchange rate predictability［J］.Journal of Economic Literature，2013，51（4）：1063-1119.

［4］ 陈平，李凯.人民币汇率与宏观基本面：来自汇改后的证据［J］.世界经济，2010（9）：28-45.

［5］ Estrella A，HardouvelisG A.The term structure as a predictor of real economic activity［J］.The Journal of Finance，1991，46（2）：555-576.

［6］ Haubrich G J，Dombrosky A M..Predicting real growth using the yield curve［J］.Federal Reserve Bank of Cleveland Economic Review，1996，32（1）：26-35.

［7］ 郭涛，宋德勇.中国利率期限结构的货币政策含义［J］.经济研究，2008，（3）：39-47.

［8］ 李宏瑾，钟正生，李晓嘉.利率期限结构、通货膨胀预测与实际利率［J］.世界经济，2010（10）：120-138.

［9］Diebold X F，Li.Forecasting the term structure of government bond yields［J］.Journal of Econometrics，2006，130（2）：337-364.

［10］Nelson R C，Siegel A F.Parsimonious modeling of yield curves［J］.Journal of Business，1987，60（4）：473-489.

［11］Chen Y C，Tsang K P.What does the yield curve tell us about exchange rate predictability？［J］.Review of Economics and Statistics，2013，95（1）：185-205.

［12］Valkanov R.Long-horizon regressions：theoretical results and applications［J］.Journal of Financial Economics，2003，68（2）：201-232.

［13］Clark T E，West K D.Approximately normal tests for equal predictive accuracy in nested models［J］.Journal of Econometrics，2007，138（1）：291-311.

Term structure of interest rate，relative factors and exchange rate prediction

LI Yana， WU Liangb

（a.School of Mathematics and Statistics；b.School of Economics，Fuyang Normal University，Fuyang Anhui 236037，China）

Since the term structure of interest rates embodies information about future economic activity，this paper uses dynamic Nelson-Siegel model to extract relative level，slope and curvature based on monthly data of interest rate of term structure of China and United States from April in 2006 to December in 2014 and analyses forecasting ability of relative factors on Renminbi/Dollar exchange rate.The empirical study shows that（1）Relative factors model can predict exchange rate changes 1 to 12 months ahead，and 1 percentage point increase in relative level or slope predicts 1%and 2%annualized appreciation of the Renminbi respectively，1 percentage point increase in relative curvature predicts 1%annualized depreciation of the Renminbi；（2）Rolling window forecasting based on Clark-West statistics shows that relative factors model outperforms random walk and uncovered interest parity model.

term structure of interest rates；dynamic Nelson-Siegel model；relative factors；exchange rate prediction

表3　RMSPE比率和相应CW统计量

F830

A

1004-4329（2016）02-092-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）02-092-05

2016-01-29

安徽省质量工程（2014msgzs153）；阜阳师范学院科研究项目（2015DJSZ05）；阜阳师范学院质量工程项目（2014JXTD01）资助。

李艳（1983－），女，硕士，助教，研究方向：高等教育经济管理。