FI-内射复形

辛大伟，田　雪

（阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

FI-内射复形

辛大伟，田雪

（阜阳师范学院 数学与统计学院，安徽 阜阳 236037）

复形范畴中的同调理论是由Cartan和Eilenberg于20世纪50年代引入的，它受到众多学者的关注。由于模的复形可以看成模的推广，因而在复形范畴中也可以开展同调理论的研究。作为FI-内射模的推广，本文定义了FI-内射复形，给出了FI-内射复形与其各个层次上的模之间的联系，利用复形的覆盖刻画了FI-内射复形，最后讨论了FI-内射复形与内射复形之间的关系。

FI-内射模；FI-内射复形；FP-内射复形

复形范畴中的同调理论是由Cartan和Eilenberg于20世纪50年代引入的。由于模的复形可以看成模的推广，因而在复形范畴中也可以开展同调理论的研究。在文献［1］中，毛立新引入了FI-内射模的概念。在此基础上，本文将FI-内射模推广到复形范畴中，定义了FI-内射复形，从覆盖和层次模角度刻画了FI-内射复形，得到了一些结果。下面列出本文需要的几个主要概念，更多的内容可以参考［2-10］。

1　预备知识

本文除非特殊指明，否则R均表示一个具有单位元的环。

称C为R-模复形［3］（简称复形），如果以下 R-模与 R-模同态的序列

其中，N在第i+1个和第i个层次。

众所周知，复形范畴中有足够的投射对象和内射对象，对于任意的复形C和D，Hom（C，D）表示所有由C和D的复形态射构成的阿贝尔群，对于任意的i＞0，Ext1（C，D）表示Hom的右导出函子。

一个左R-模M称为FI-内射模［1］，如果对于任意的FP-内射模（K，M）=0。

复形C称为FP-内射复形［5］，如果对于任意的有限表现复形。复形C的FP-内射维数，记作FP-id（C），是指对于任意的有限表现复形D，满足Extn+1（D，C）=0成立的最小正整数n。如果满足条件的n不存在，则规定FP-id（C）=∞

2　主要定理与证明

定义1设C是一个复形，若对于任意的FP-内射复形G，Ext1（G，C）=0，则称C为FI-内射复形。易见，内射复形是FI-内射复形。

下面的定理给出了FI-内射复形与其各个层次上的模之间的关系。

定理1设C是一个左R-模复形，则以下条件等价：

（ⅰ）C是FI-内射复形；

（ⅱ）对于任意的i∈Z，Ci是FI-内射R-模，且对于任意的FP-内射复形L，复形︵Hom（L，C）正合。

证明（ⅰ）⇒（ⅱ）设

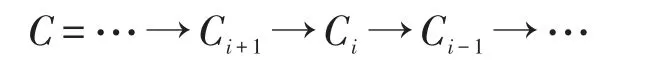
是FI-内射复形。设N是FP-内射模，0→Ci→Y→N→0是模范畴中任意扩张。利用推出图可得到下面的交换图。于是得到复形

从而我们有复形正合列

因为Di-1（N）是FP-内射复形，所以（1）是可裂的。因此，R-模正合列0→Ci→Y→N→0可裂，即。故Ci是FI-内射模。

设 L是 FP-内射复形，对任意的i∈Z，f:L→C［i］是复形的映射。因为C是FI-内射复形，所以复形正合列是可裂的，从而复形正合列可裂。于是，f同伦于0。因此，复形）正合。

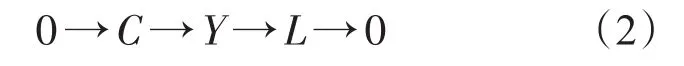
（ⅱ）⇒（ⅰ）设L为FP-内射复形，是复形范畴中的任意扩张。因为C每个层次上的模Ci都是FP-内射模，所以正合列（2）在模层次上是可裂的。因此，正合列（2）同构于复形正合列

定理2设C是一个左R-模复形，则以下条件等价：

（ⅰ）C是FI-内射复形；

（ⅱ）对于任意的复形短正合列0→C→M→H→0，其中M为FP-内射复形，则M→H是H的FP-内射预盖；

（ⅲ）存在一个L的FP-内射预盖φ:K→L，其中K为内射复形，使得C=Kerφ；

(ⅳ)对于任意的复形短正合列

0→A→L→N→0，其中 N为FP-内射复形，则0→Hom（N，C）→Hom（L，C）→Hom（A，C）→0是正合的。

证明 (ⅰ)⇒(ⅱ)和(ⅰ)⇒(ⅳ)显然。

(ⅱ)⇒(ⅲ)由文献［3］，复形的内射预包络是存在的，从而存在复形的正合列

(ⅲ)⇒(ⅰ)设C是FP-内射预盖φ:K→L的核，其中K为内射复形，则有复形正合列

0→C→K→Imφ→0。

注意到，K→Imφ是一个FP-内射预盖。对任意的FP-内射复形G，复形序列Hom（G，K）→Hom（G，Imφ）→Ext1（G，C）→Ext1（G，K）=0是正合的。根据Hom（G，K）→Hom（G，Imφ）的正合性，有Ext1（G，C）=0。因此，C是FI-内射复形。

(ⅳ)⇒(ⅰ)设复形序列0→A→P→N→0是正合的，其中P为投射复形，N为FP-内射复形。对任意的FP-内射复形G，存在正合列Hom（P，C）→Hom（A，C）→Ext1（N，C）→Ext1（P，C）=0

根据(ⅳ)，得到Ext1（N，C）=0。因此，C是FI-内射复形。

命题1设R是左凝聚环，则以下条件等价：

(ⅰ )左R-模复形C是内射的；

(ⅱ)C是FI-内射复形，且FP-id（C）≤1；

证明（1）⇒(ⅱ)显然。

(ⅱ)⇒(ⅰ)设C是FI-内射复形，且FP-id（C）≤1，则有复形正合列

0→C→E→N→0，（4）

其中E是内射复形。因为内射复形是FP-内射的，所以由(ⅱ) 知，N是 FP-内射复形。故，Ext1（N，C）=0。于是，复形正合列（4）是可裂的，故而C是内射复形。

［1］ Mao L X，Ding N Q.FI-injective and FI-flat modules ［J］.Journal ofAlgebra，2007，309（1）：367-385.

［2］ Enochs E E，Jenda O G.Relative homological algebra（Ⅰ）［M］.Berlin：De Gruyter Expositions in Mathematics 30，2000：105-125.

［3］ Enochs E E，Jenda O G.Relative homological algebra（Ⅱ）［M］.Berlin：De Gruyter Expositions in Mathematics 54，2011：1-36.

［4］Garcia R R.Covers and envelopes in the category of complexes of modules［M］.London：Chapman&Hall/ CRC，1999：1-90.

［5］ Wang Z P，Liu Z K.FP-injective complexes and FP-injective dimension of complexes［J］.Journal of the Australian Mathematical Society，2007，91（2）：163-187.

［6］ Yang X Y，Liu Z K.FP-injective complexes［J］.Communications inAlgebra，2010，38（1）：131-142.

［7］ Zeng Y D，Chen J L.Envelopes and Covers by Modules of Finite FP-Injective Dimensions［J］.Communications inAlgebra，2010，38（10）：3851-3867.

［8］ Wang Z P，Liu Z K.Complexes of gorenstein flat modules and gorenstein cotorsion modules［J］.Communications inAlgebra，2010，38（10）：3752-3766.

［9］ Xin D W，Chen J L，Zhang X X.Completely W-resolved complexes［J］.Communications in Algebra，2013，41（3）：1094-1106.

［10］Xin D W，Chen J L，Zhang X X.On gorenstein FP-injective and gorenstein flat complexes［J］.Communications inAlgebra，2013，41（4）：1247-1267.

FI-injective complexes

XIN Da-wei，TIAN Xue

（School of Mathematics and Statistics，Fuyang Normal University，Fuyang Anhui 236037，China）

In the 1950s，Homology theory in the category of complexes was introduced by Cartan and Eilenberg.It has drawn wide attentions from more and more scholars.Since complexes of R-modules can be seen as a generalization of modules，relative homology theory of the category of modules can be generalized to that of complexes.As a generalization of FI-injective module，FI-injective complex is defined.The connection between FI-injective complex and modules of degree n is obtained，for all n in Z.FI-injective complex is discussed through covers.Furthemore，the relation between FP-injective complex and injective complex is given.

FI-injective module；FI-injective complex；FP-injective complex

O154.2

A

1004-4329（2016）02-001-03

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）02-001-03

2016-01-03

国家自然科学基金项目（11201063）；安徽自然科学基金项目（1508085MA12）；安徽省高校省级自然科学研究项目（2014KJ004）；阜阳师范学院科学研究项目（2013FSKJ13）资助。

辛大伟（1981－），男，博士，讲师，研究方向：同调代数。