基于高斯模型对空气污染扩散问题的研究

高　梦， 朱家明，刘　新，刘凤志

（安徽财经大学 a.管理科学与工程学院；b.统计与应用数学学院，安徽 蚌埠 233030）

基于高斯模型对空气污染扩散问题的研究

高梦a， 朱家明b*，刘新b，刘凤志a

（安徽财经大学 a.管理科学与工程学院；b.统计与应用数学学院，安徽 蚌埠 233030）

针对京津冀地区的空气污染问题，综合利用了空气污染指数法、变异系数法等方法，构建了模糊综合评价模型、高斯烟羽模型、多点源高斯迭加模型等模型，利用MATLAB、VC++等软件，得出影响京津冀地区空气质量的主要污染源为燃煤和汽车尾气，北京市二环、四环、六环路在16日的空气质量状况均为轻度污染等结论。并给出了河北某工厂方圆51 km内污染物浓度分布情况和北京市三个环路的空气污染浓度梯度变化情况。

空气质量指数；变异系数；单点源高斯烟羽模型；多线源高斯迭加模型；MATLAB

近十年来，我国经济水平快速增长，但由于经济增长模式相对落后，对生态平衡和自然环境造成了一定的破坏，空气污染问题日益严重。我们以京津冀地区为例，对其空气质量状况及空气污染扩散问题进行了研究（详见2015年第十二届五一数学建模联赛B题［1］）。

1　空气质量等级的衡量

1.1空气污染指数的计算

设第k种污染物的浓度为Ck，当时，其分指数Ak为其中Ak为第k种污染物的污染分指数，Ck为第k种污染物的浓度监测值，Ak，s为第k种污染物s转折点的污染分项指数值，Ak，s+1为第k种污染物s+1转折点的污染分项指数值，Ck，s为第s转折点上k种污染物（对应于 Ak，s）浓度限值，Ck，s+1为第s+1转折点上k种污染物（对应于Ak，s+1）浓度限值［2］。Ck，s和Ck，s+1的值可通过查阅国标和美标得出。

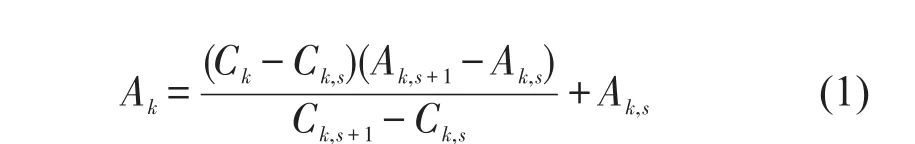
空气污染指数API为各种污染物空气污染分指数的最大值，即有

API=max（A1，A2，…，Ak，…，An），其中，Ak为第k种污染物的空气污染分指数，n为污染物的个数。

1.2空气质量优劣程度等级的评定

根据空气污染指数与空气质量级别的对应关系，进行空气质量优劣程度等级的评定，具体对应关系如表1。

2　京津冀地区主要污染源及其污染参数的分析

2.1研究方法

在中国空气质量在线监测分析平台查找到2014年度北京、天津、石家庄等地区空气污染物在各个月的浓度值。利用变异系数法，以PM2.5、PM10、二氧化氮、二氧化硫、一氧化碳、臭氧的浓度值为指标对北京、天津、石家庄进行模糊综合评价［3］。得出各地区指标的权重（见表2）。

表1　空气污染指数与空气质量级别对应关系表

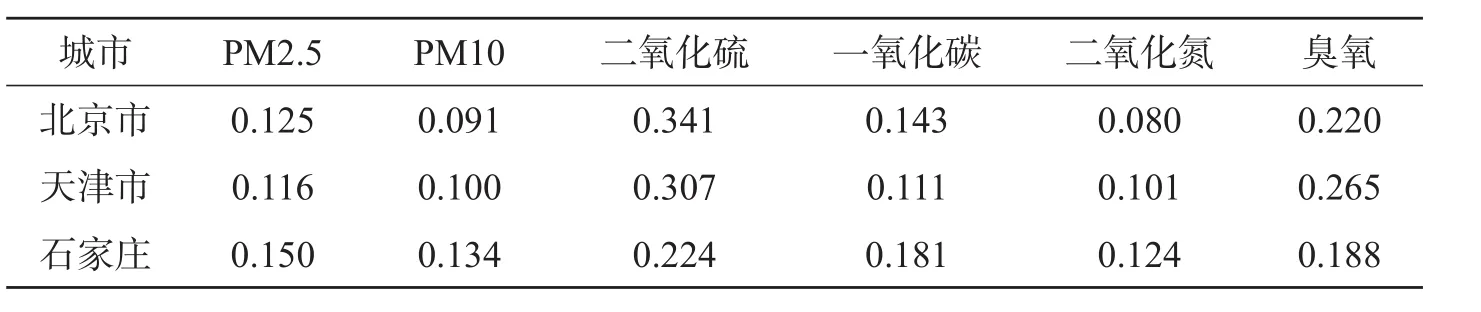
表2　京津冀地区各污染物指标的权重值表

2.2结果分析

从表2可以看出京津冀地区的首要污染物为二氧化硫，次要污染物为臭氧。

二氧化硫主要来源于煤、石油等燃料的燃烧以及燃煤电厂排放的废气。京津冀地区是全国主要的高新技术和重工业城市，煤炭发电占据着非常重要的地位。而煤炭中，硫为最主要的有害成分，煤炭燃烧时绝大部分的硫被氧化成二氧化硫，随烟气排放，污染大气，引起雾霾。而一氧化碳和一氧化氮易被空气中的氧气氧化，因而在测得的空气质量指数中浓度较低。

臭氧主要来源于汽车尾气，汽车尾气中的碳氢化合物和氮氧化合物在光照作用下发生化学反应生成臭氧，臭氧会和大气中的其它成份结合形成光化学烟雾，这是汽车尾气最主要的危害形式。汽车尾气主要污染物为一氧化碳、碳氢化合物、氮氧化物（NOx）、铅等，还含有较多的二氧化硫和悬浮颗粒物（PM2.5，PM10）。

3　对单污染源空气污染扩散问题的研究

3.1研究思路

烟羽模型适用于连续源的扩散，其浓度分布公式为：

其中，c为扩散的污染物浓度，A为烟囱排放污染物的强度（单位为m3/s），v为平均风速，h为烟云的有效高度，（x，y，z）是该点坐标，σy，σz分别为横风向和垂直方向的扩散系数，单位为m［4］。

以烟囱塔在地面上的垂直投影点为原点，以风速方向为x轴正向，y轴在水平面上垂直于x轴，正向在x轴的左侧，z轴垂直于水平面XOY，向上为正向，建立空间直角坐标系。

由于题中未给出烟囱排放污染物所含的初始能量，以及烟囱口的直径等条件，所以无法求出排放的烟云抬升的高度h，因此以烟囱的高度H（H= 50 m）来表示有效高度h。假设模型中的大气稳定度为中性气象条件D，根据σy、σz与大气稳定度及下风距离x的关系［5］（见表3）计算得σy和σz。

表3　扩散系数计算方法表

3.2研究方法及结果分析

3.2.1污染物浓度分布情况

根据公式（2），利用MATLAB编程作出在早上9点至下午3点期间（见图1，2）和在晚上10点至凌晨4点期间（见图3，4）该工厂附近51 km内废气扩散模拟图和污染物浓度分布模拟图。

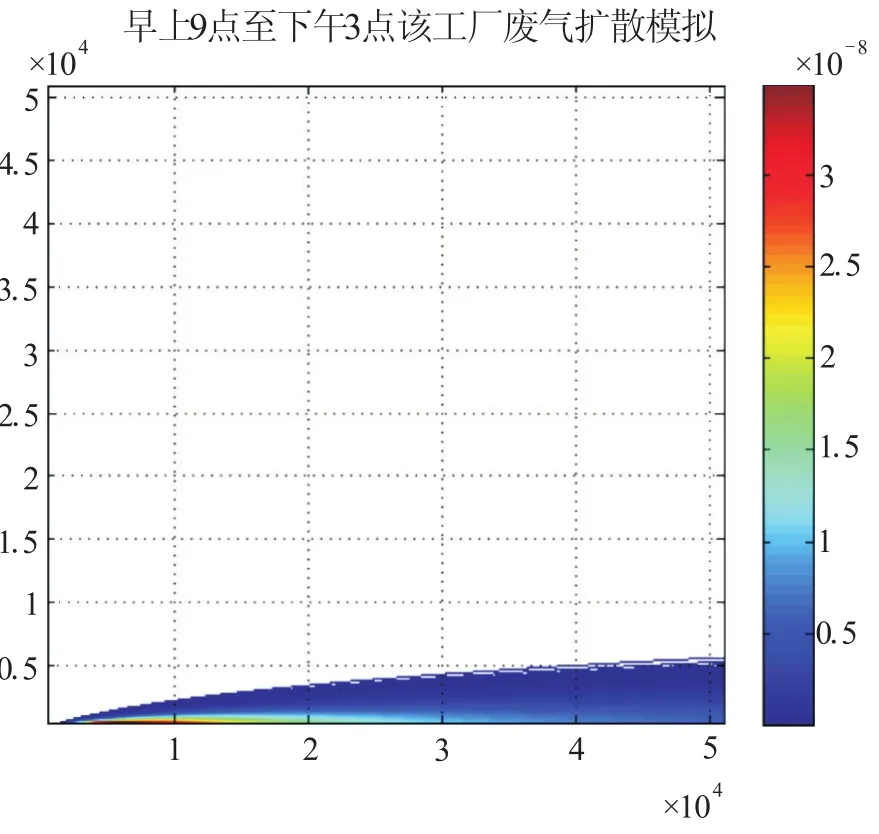
图1　早上9点至下午3点废气扩散模拟图

图2　早上9点至下午3点污染物浓度分布模拟

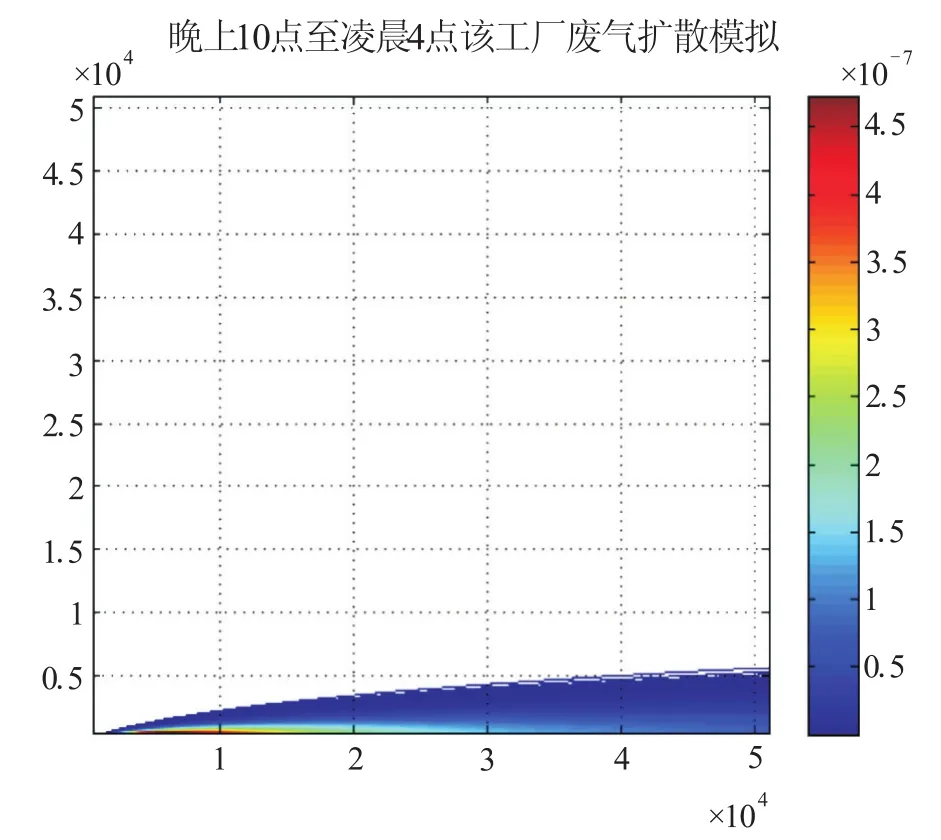
图3　晚上10点至凌晨4点废气扩散模拟图

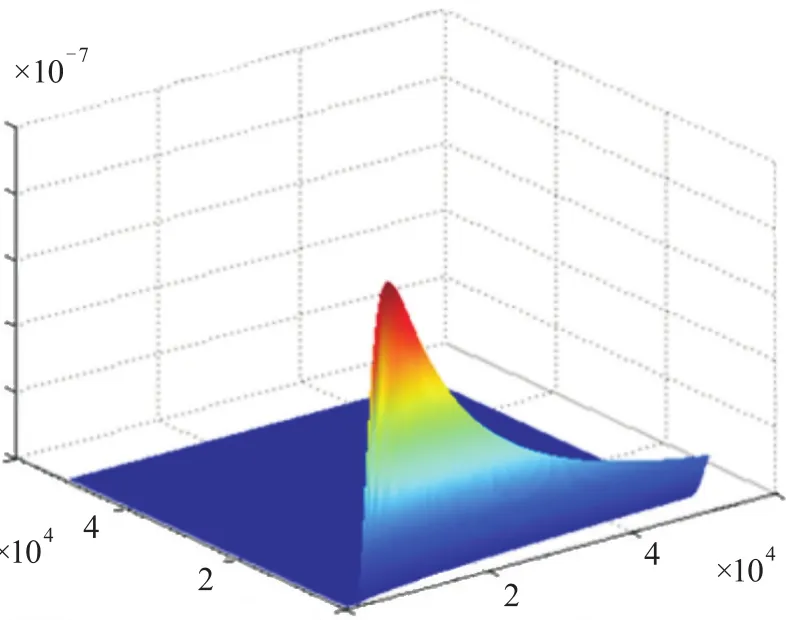
图4　晚上10点至凌晨4点污染物浓度分布模拟图

以上两个时间段均为污染物连续排放期间，由废气扩散模拟图和污染物浓度分布模拟图可以看出，在最靠近污染源处污染物浓度最大，随着下风距离的增加，污染物浓度逐渐减小。由于本题设定风速为6 m/s且忽略污染物在无风时的自然扩散速度，因此污染物主要沿着x轴，即风向方向扩散，在污染物浓度分布模拟图中表现为浓度主要分布在x轴，而在其它位置浓度为零。

在早上8点时，考虑晚上10点至凌晨4点期间。在凌晨4点时，该工厂方圆51 km内浓度分布情况见图4。本题忽略污染物在无风时的自然扩散速度，仅考虑污染物烟团随风向整体飘动，凌晨4点至早上8点期间污染物移动距离为s=v×t=6×4×3 600=86 400m。其中，s为污染物移动距离，v为平均风速，t为污染物移动时间。

可以看出污染物移动距离为86.4 Km，大于51 km，所以早上8点时，方圆51 km范围内不存在污染物，污染物浓度均为零。

在中午12点时，因为中午12点在早上9点至下午3点期间内，所以其空气污染浓度分布与早上9点至下午3点期间空气污染浓度分布相同，见图2。

在晚上9点时，考虑早上9点至下午3点期间，在下午3点时，该工厂方圆51 km内浓度分布情况见图2，下午3点至晚上9点期间污染物移动距离为s=μ×t=6×6×3 600=129.6km。移动距离大于51 km，所以晚上9点时，方圆51 km范围内不存在污染物，污染物浓度均为零。

3.2.2空气质量等级的求解

根据单污染源高斯烟羽模型及公式（2），编写C++程序得到在早上9点至下午3点期间和晚上10点至凌晨4点期间距工厂废气排放点不同距离时的空气污染浓度C（xk，yk，z）（z取50）。可得，在早上9点至下午3点，该工厂排放浓度为406.92 mg/m3，排放速度为1 200 m3/h时有：

因为污染物主要为氮氧化物，所以此分指数即为其空气污染指数。根据空气污染指数与空气质量等级的对应关系，得此时该工厂方圆51 km内空气质量等级为I，空气质量状况为优。

同理可得，在晚上10点至凌晨4点期间，其污染物的平均浓度2.57×10-36μg/m3，二氧化氮的空气质量分指数为3.21×10-36，空气质量等级为I，空气质量状况为优。

此结果与我们正常理解不符，即有工厂废弃污染，但空气质量状况却很好。但此题仅考虑了该工厂一个污染源，忽略了该地区其它工厂及机动车尾气对空气质量的影响，而此工厂污染物的排放浓度和排放速度均较小，且计算的扩散范围较大，所以对空气污染不大，空气质量较好。

由3.2.1中污染物浓度分布情况的求解结果可知，早上8点和晚上9点时该工厂方圆51 km内不存在污染物，所以其空气质量等级为I，而中午12点时，该工厂方圆51 km内空气污染浓度分布情况为图2所示，其空气质量等级为I。所以，三个时点所求范围内的空气质量等级均为I，空气质量状况为优。

4　对多污染源空气污染扩散问题的研究

4.1研究思路

针对机动车排放污染，当风向与线源垂直的时候，得到无限长线源的扩散模式，其公式为

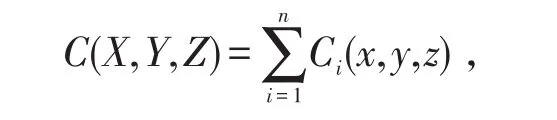
并且

以第i个污染源所在的位置为坐标原点，以风向方向为x轴正方向，y轴与x轴形成右手坐标系，建立空间直角坐标系。Ci（x，y，z）为第i个污染源在点（x，y，z）处的空气污染浓度（mg/m3），x为下风向距离（m），y为横截风向距离（m）；z为距地面高度（m）；Ai为污染物源强（mg/s）；v为排气口处的平均风速（m/s）；σy、σz分别为水平方向和垂直方向扩散系数（m），它们是下风向距离x及大气稳定度的函数；h为污染源有效排放高度［6］。

4.2研究方法及结果分析

4.2.1空气污染浓度梯度变化的求解

北京市外环路与市中心的距离（km）如表4。

表4　北京市外环路与市中心的距离（km）

根据表4求出二环与四环的距离、四环与六环的距离、以及二环和六环的距离，分别为S1=5.4 km、S2=15.2 km、S3=20.6 km。

设二环、四环和六环排放浓度分别为156 μg/ m3、136 μg/m3和100 μg/m3，三个环路的排放速度均为1 m3/s，可得三个环路的污染物源强分别为156μg/s、136μg/s和100μg/s。根据现有资料做出北京2015年1月16日当天的平均风速为8 m/s的合理估计。由帕斯奎尔法［7］确定大气稳定度为中性，即为大气稳定度等级为D。

根据公式（3），计算得环路4和环路6在环路2处的浓度分别为0.081 561μg/m3和0.025 726 μg/m3，因此环路 2的汽车尾气总浓度为C0，1=156+0.081 561+0.025 726=156.107 3μg/m3。

同理可得，环路2和环路6在环路4处的浓度分别为0.081 561μg/m3和0.030 141μg/m3，环路4的汽车尾气总浓度为136.111 7μg/m3。

环路2和环路4在环路6处的浓度分别为0.040 133μg/m3和0.040 992μg/m3，环路6的汽车尾气总浓度为100.081 1μg/m3。

根据各环路的汽车尾气总浓度绘制北京市在16日的空气污染浓度梯度变化图，见图5。

图5　空气污染浓度梯度图

由图5可得，从二环路到六环路空气污染浓度梯度呈下降趋势，且从四环路到六环路下降趋势增大。这主要因为，二环、四环和六环路距离市中心的距离逐渐增大，因此车流量逐渐减小，空气污染浓度梯度呈下降趋势。

4.2.2空气污染质量等级的求解

因为汽车尾气中最主要的污染物是氮氧化物，根据国标中二氧化氮的浓度范围求出其空气污染分指数。由公式（1）得二环路空气污染分指数A1为

同理得四环路的空气污染分指数A2为128，六环路的空气污染分指数A3为110。因为氮氧化物为主要污染物，所以二、四、六环路的空气污染指数与其空气污染分指数相同，分别为138、128、110，根据空气污染指数与空气质量等级的对应关系，得三个环路在16日的空气质量等级均为III级，空气质量状况为轻度污染。

5　小结

以上各模型在建模过程中通过多种相应的软件检验，具有一定的合理性。本文以京津冀地区为例，对空气质量状况及空气污染扩散问题进行了研究，得出了影响京津冀地区空气质量状况的主要污染源及污染参数，并给出了计算空气质量状况的方法，有利于该地对环境的治理。另外，本文的模型对于其它地区空气污染状况的研究及环境治理也有一定的参考作用。

［1］ 2015年五一数学建模联赛B题.http：//doc.guandang.net/sf441fc7489b58db2c3aa645f.html.

［2］ 惠学香.空气污染指数简易计算方法［J］.环境监测管理与技术，2002，14（1）：39-40.

［3］ 杨桂元.数学建模［M］.上海：上海财经大学出版社，2015：128.

［4］ 郭遵强.大气污染扩散模型的研究及在环境应急系统中的实现［D］.青岛：中国海洋大学，2008.

［5］ 李玉平.计算大气扩散系数的一组经验公式［J］.北京理工大学学报，2009，29（10）：914-917.

［6］ 胡亚，林珲，徐丙立，等.基于PC机群的多点源高斯大气污染扩散模型的并行计算研究［J］.高技术通讯，2010，20（4）：436-440.

［7］ 李小忠，侯祺棕，高燕，等.城市大气稳定度分级模型的研究［J］.工业安全与防尘，2001，27（4）：27-31.

Research of air pollution diffusion problem based on Gaussian model

GAO Menga， ZHU Jia-mingb*，LIU Xinb，LIU Feng-zhia

（a.School of Management Science and Engineering；b.School of Statistics and Applied Mathematics，Anhui University of Finance& Economics，Bengbu Anhui 233030，China）

In view of the problem of air pollution in Beijing-Tianjin-Hebei region，comprehensive utilization of the air pollution index method，the variation coefficient method and other methods，this paper constructs the fuzzy comprehensive evaluation model，Gaussian plume model，Gaussian superposition model and so on，using the MATLAB and VC++software，concluded that the main sources of affecting air quality in Beijing-Tianjin-Hebei region are coal and car exhaust，and the air quality on second，fourth，sixth loop of Beijing in 16 are light pollution，etc.Then we gave the pollutant concentration distribution around 51 kilometers'by a factory in Hebei province and the change of air pollution's concentration gradient in Beijing's three loops.

air quality index；coefficient of variation；single point source Gaussian plume model；line source superposition Gaussian model；MATLAB

X823

A

1004-4329（2016）02-012-05

10.14096/j.cnki.cn34-1069/n/1004-4329（2016）02-012-05

2015-12-03

国家自然科学基金（11301001）；国家级大学生创新项目（201510378020）资助。

朱家明（1973－），男，硕士，副教授，研究方向：应用数学与数学建模。Email：zhujm1973@163.com。